电动汽车换电电池冗余度及充电规模研究

符 杨，邱 云，郑志敏，励文伟

(1.上海电力学院电气工程学院，上海200090；2.浙江省电力公司宁波供电公司，浙江宁波315010)

电动汽车换电电池冗余度及充电规模研究

符 杨1，邱 云1，郑志敏2，励文伟2

(1.上海电力学院电气工程学院，上海200090；2.浙江省电力公司宁波供电公司，浙江宁波315010)

电动汽车蓄电池成本占整车成本约三分之一，因此规模化应用之后，针对电动汽车换电站不同时段的蓄电池储备量及充电设备规模的优化研究对提高换电站建设运营的经济性及促进电动汽车的发展具有重大意义。提出了换电站蓄电池冗余度的概念，建立了基于一定用户换电需求和换电站充电管理策略下，换电站充电设备规模和蓄电池冗余度需求模型。应用蒙特卡洛(Monte Carlo)方法进行仿真计算，得出换电站不同充电设备规模下的储备蓄电池冗余度。算例分析表明，所提方法在充电设备规模增长初期可以大幅减少电池冗余度，达到相应规模之后还能提升可用于优化控制充电的蓄电池的数量和电量裕度。

电动汽车；换电模式；充电设备；电池冗余度；蒙特卡洛法

随着全球气候变暖和化石燃料短缺，电动汽车的研究和推广应用受到了越来越多的重视。目前，电动汽车能源供给方式主要分为充电模式和换电模式两种[1]。充电模式指电动汽车采用整车充电，按充电功率和时间分为快速充电和常规充电。换电模式指采用更换电池的方式为电动汽车提供能源补给，在换电站对电池进行集中充电。国家电网公司和南方电网公司对换电模式高度重视，在2011年提出以换电为主的电动汽车运营模式。电动汽车规模化应用后，必然带来蓄电池充电和数量储备问题[2]。如果换电站内充电设备的规模不足或者储备满电量的蓄电池数量不够，会导致部分电动汽车换电需求在某一时刻无法得到满足。相反，充电设备的过度建设以及电池的数量过多所造成的财力上的浪费，必然会降低电动汽车运营的经济性。因此，有必要展开针对电动汽车换电站充电设备规模和储备电池冗余度的研究。

在电动汽车换电站充电需求和管理方面，国内外学者已经开展了相关研究，但针对电池及充电设备数量的优化研究较少。文献[3]总结了电动汽车及充电站在我国的建设现状，分析了影响电动汽车充电的因素以及充电站布局原则。居民负荷分布近似于电动汽车的负荷分布，文献[4]利用居民负荷的分布情况模拟电动汽车负荷分布来确定候选地址的权重，使用层次分析法，以电动汽车分布情况、充电站安装费用等为约束条件，以经济性最优作为目标函数，通过优化方法，建立优化模型来解决电动汽车充电站的选址、定容问题。文献[5]借用了数学中的装箱问题来解决电动汽车蓄电池数量规划，提出了近似着色法、首次适应下降算法(FFD)以及双模态启发式算法(BMH)这3种方案来解决电动汽车电池规划问题。文献[6]提出了换电充裕度的概念，在无序充电模式下通过蒙特卡洛(Monte Carlo)方法，基于电动汽车用户的用车习惯来模拟求得不同时间段内换电站所需储备的蓄电池数目，但没有考虑充电设备的规模约束可能带来的电池冗余度的增加。

在上述研究基础上，本文针对换电模式下充电规模和电池冗余度需求，同时考虑充电设备容量约束和换电需求约束，建立充电设备规模和电池冗余度需求模型，采用Monte Carlo仿真方法来验证上述模型的有效性，并针对不同方案的结果进行讨论。

1 电池冗余度及充电规模的影响

在换电模式下，换电站电池冗余度是为满足换电站任意时刻电动汽车换电需求所需储备冗余的满电量电池的数量。能否满电动汽车换电需求，主要的影响因素是t时刻换电所需电池组数量以及换电站所能提供的满电电池数量。用数学公式表示如下：

式中：Nleft(t－1)表示换电站满足电动汽车在t－1时刻的换电需求后，所剩余的储备蓄电池数量；N(t)表示换电站在t－1时刻尚未充满电，在t－1到t时间段电量达到满负荷的电池数目；R(t)表示在t时刻电动汽车所需更换的电池数量，即t时刻换电需求。

Nleft(t－1)主要取决于电动汽车换电需求以及蓄电池的充电管理策略。N(t)不仅受到上一时刻换电站内尚未充满电的电池数目的约束，同时电动汽车换电站的充电规模有限，换电站在同一时刻无法对所有未满电电池组进行充电。若充电设备规模不足，充电高峰时换下的电池无法得到即时充电，导致后续必须投入新的冗余满电蓄电池来满足换电需求。由于目前充电设备和电池成本昂贵，因此无论换电站充电设备规模过剩，还是储备电池冗余度过高，都将降低电动汽车运营的经济性。

2 换电站充电规模和电池冗余度模型的建立

由式(1)可知影响电动汽车换电站充电规模和电池冗余度指标的主要因素是t时刻电动汽车换电需求和换电站充电功率及电池数量。换电需求取决于电动汽车的数量、用户出行特征和行驶里程等因素。换电站充电规模和电池冗余度相互契合，以满足电动汽车换电需求。结合换电模式自身特点，本文对电动汽车换电需求和换电站充电做出了如下假设。

2.1 电动汽车换电需求建模

由式(1)可得，计算电动汽车的换电需求，必须先建立电动汽车日功率消耗模型，本文针对单台电动汽车日功率消耗模型做出如下假设。

(1)假定电动车辆对传统车辆的替代使用不会影响用户出行特征，根据美国交通部2009年对全美家用车辆的调查结果[7-9]，采用文献[10]的方法对调查结果进行分析，得到电动汽车每次行驶里程总数以及每小时行车占总里程百分数。

归一化处理单台汽车日行驶里程统计数据，并用极大似然估计的方法将其近似为对数正态分布。处理后，单台汽车日行驶里程概率密度函数如下所示：

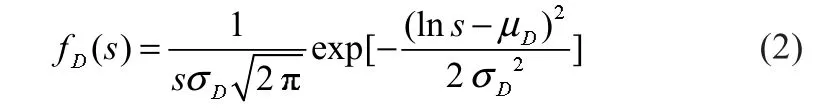
文献[9]给出了普通家用汽车每小时行驶距离占每日总里程比例的统计结果。由于直接拟合该数据会带来较大误差，并且本文所关心的是时间段电池冗余度，因此采用离散化变量来表示汽车每小时行驶距离所占百分比数fs(t)，如表1所示。

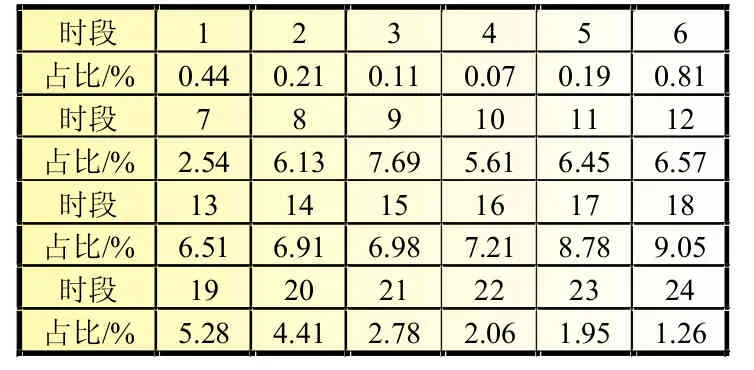
表1 汽车每小时行驶距离占比

离散化处理后，电动汽车在一天中的总行驶里程可以表示为：

式中：Si0为第i台电动汽车在某日的总行驶里程。

(2)本文针对某一特定类型的电动汽车开展研究，并假设汽车电池满电量的平均额定容量为C(单位kWh)。为防止电池过度放电对电池寿命的损害，当电池剩余电量为kC(k＜1)车主会选择更换电池。该车型的每百公里耗电量(单位kWh)为W100。由于电动汽车换电所需要的时间数量级为分钟，并且本文讨论的是一天内各个时段的电池储备数目，因此把1天分为24 h时间段，单台电动汽车换电池时不考虑换电时间的影响。

(3)每辆电动汽车的日行驶里程等用户驾车出行特征均为相互独立的随机变量。

(4)假设被更换下来的电池，在有空闲充电桩的情况下，在换电站内立即采用慢充模式充电，直至满电；如充电桩没有空余位置，则进入等待充电队列。

2.2 换电站充电约束

电动汽车换电站对蓄电池充电的约束条件主要为换电站充电功率约束和最低保障换电需求储备电池约束。

(1)换电站电池充电功率约束

式中：Pt为换电站在t时刻的充电功率；Pit为第i座充电桩在t时刻充电的功率，其取决于电池型号、电量以及充电设备功率；Ptmax为换电站在t时刻的最大充电功率，其取决于充电桩的总数及其功率，以及t时刻换电站所在电网能承受的最大负荷；Ptmin为换电站在t时刻的最小充电功率。本文没有考虑电动汽车在电网高峰时段向电网倒送电的情况，因此最小充电功率设定为0，即没有充电桩工作。

(2)最低保障换电需求储备电池约束

在式(1)中，满足t－1适合换电需求后剩余的蓄电池数目和t－1到t时间段所充满电的电池数目必须大于t时刻需要更换电池的电动汽车数量，否则投入新的满电量蓄电池。

(3)充电功率与充电电量的关系

式中：ΔQit为第i块电池在t时段内的充电量；Qit为第i块电池在t时刻的电量；t为充电时间，本文取1 h；C为电动汽车蓄电池额定满电量。

2.3 求解方法

本文采用Monte Carlo方法，以1 h为单位，模拟求解每日24个时段电动汽车换电需求及换电站充电负荷和电池冗余度。其具体步骤如下：

(1)输入参数，初始化电动汽车蓄电池以及换电站充电桩状态。

(2)根据式(2)～式(4)模拟电动汽车行驶里程，当电池电量不足kC时更换电池。若无满电蓄电池，投入新的满电量电池池以满足换电需求。

(3)更换下电池后根据式(5)～式(8)约束在换电站充电，若无空闲充电桩排队等待至下一时刻。

(4)统计电动汽车换电需求、换电站充电负荷及储备电池数目。

算法流程如图1所示。

图1 程序流程

3 算例仿真

本算例以10 000辆电动汽车作为样本数量，电动汽车百公里耗电量W100为15 kWh，C取30 kWh，k=0.2。为了消除初始电池电量对仿真结果的影响，连续计算15天，并将每一天最后24时刻电池电量作为第二天0时刻初始电量，把第15天的仿真结果作为最终结果。单座充电桩最大功率为3.75 kW。分别计算电池充电桩在600～900座时为保障换电需求电动汽车的电池冗余度，计算结果如图2所示。

由图2可得第15天24个时刻的换电需求，在上午9点和下午18点左右形成两拨换电高峰。每辆汽车日换电期望次数为0.267 3次。各充电规模换电站的日换电需求曲线一致。

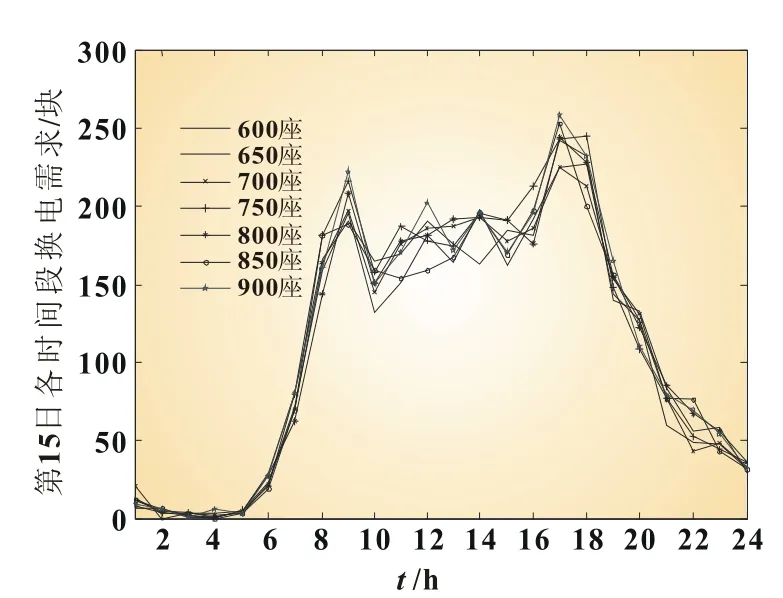
图2 第15日各时刻换电需求曲线

图3 第15日各时刻换电站充电负荷曲线

由于电动汽车充电具有一定的延续性，因此如图3所示，换电站的充电负荷高峰延后于换电需求早上9点和下午18点的换电高峰，在早上11点左右到达充电高峰，23点左右结束充电高峰，在早晨7点左右达到充电负荷的低谷，此时大部分储备电池已经充满，可以迎接换电早高峰。充电负荷峰谷的情况和充电管理策略和换电需求直接相关。由曲线可得，换电站在600～650充电桩规模下，始终高负荷甚至满负荷运作，没有裕度来进行优化充电控制。

结合图3和图4可知，在600座充电桩时，即使在充电桩满负荷工作的情况下，也无法满足电动汽车换电的基本要求，必须不断投入新的储备电池，因此该方案无法在实际运营中满足电动汽车换电需求和换电站经济性要求。充电规模在650座时，日所需最大储备电池数在11日以后达到稳定，即可以满足电动汽车换电需求，但换电站始终工作在高负荷工况，没有电池和充电设备裕度投入优化控制充电。随着充电规模的增加，储备电池冗余度也随着减少。此外，通过仿真可以得到不同时间段换电站内所需投入储备电池的冗余度，如图5所示。

图4 日所需最大储备电池数

表2 充电规模对冗余度和可优化利用充电功率影晌

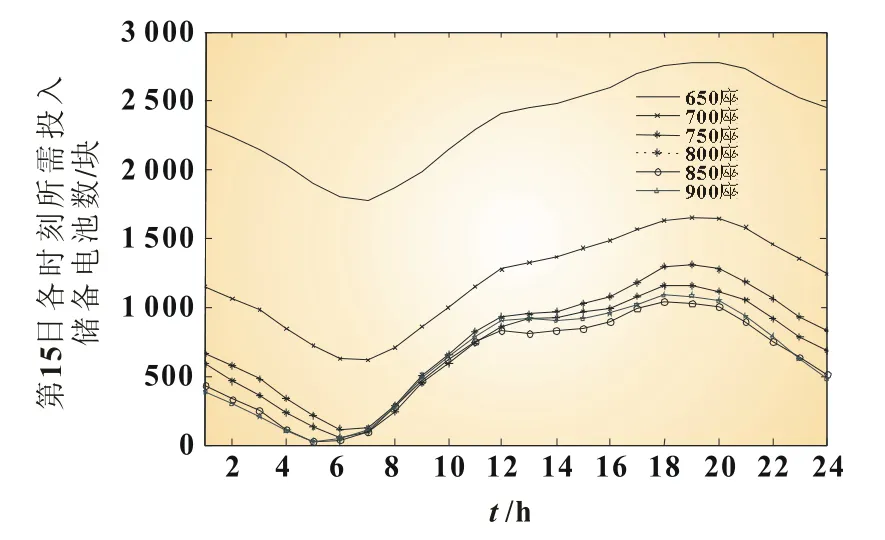
图5 第15日各时间段所需储备电池数量

由表2可得换电站充电规模对冗余度和可优化利用充电功率的影响。换电站规模低于750座充电桩时，随着充电设备数量和功率的增加，需要的蓄电池冗余度大幅减少；反之，换电站规模高于750座充电桩时，充电设备的增加对减少电池冗余度效果削弱，并在850座充电桩规模时达到饱和。可优化利用充电功率和占总功率百分比始终随着充电设备规模而提升。

本文仿真表明，对于10 000辆电动汽车样本点，在充电设备增加的初期，可以大幅减少电动汽车电池冗余度，同时增加可利用优化控制充电裕度，提高了换电站经济性。充电设备规模高于某一水平后，电池冗余度受必须满足换电需求的约束无法继续提升。因此，合理规划充电站设备规模和电池冗余度，对提升换电站经济性具有很大的效果。同时，在直接充电管理策略情况下，在电网负荷的低谷阶段，电动汽车换电需求少，富余的电池较多，因此不需要电动汽车入网给电网倒送电能(vehicles to gird，V2G)；在电网负荷的高峰阶段，电动汽车充电负荷和电网高峰重叠，换电需求高，可用充满电的蓄电池少，若电池冗余度不足几乎没有电池余量能够投入V2G。其原因主要包括车主用电习惯、电池充电管理策略、换电站充电设备的容量和数量约束。因此，本文所提出的换电站充电规模和电池冗余度需求模型也可以用于评价优化控制模式下蓄电池的电量裕度和充电管理策略的优劣。

4 结论与展望

本文分析了换电模式下电动汽车充电规模和电池冗余度的需求特性，建立基于电动汽车换电需求的换电站充电规模和电池冗余度的需求模型。通过Monte Carlo方法，得出不同换电站充电设备规模及各时刻所需满足换电需求的储备电池数量。结果表明，换电站充电设备容量的提升初期可以大幅减少电池冗余度，提高换电站经济性，后期还可提升优化控制模式下蓄电池的电量裕度。换电站可根据本地电网情况和电动汽车换电需求、分时电价以及设备造价等优化配置换电站的充电设备规模和电池冗余度，提高运营经济性。

本文采用充电设备和电池冗余度模型也适用于电动汽车优化控制充电运营模式。

[1]陈良亮，张浩，倪峰，等．能源根据设施建设现状与发展探讨[J]．电力系统自动化，2011，35(14)：11-17．

[2]张文亮，武斌，李武峰，等．我国纯电动汽车的发展方向及能源供给模式的探讨[J]．电网技术，2009，33(4)：1-5．

[3]徐凡，俞国勤，顾临峰，等．电动汽车充电站布局规划浅析[J]．华东电力，2009，37(10)：1678-1682．

[4]寇凌峰，刘自发，周欢．区域电动汽车充电站规划的模型与算法[J]．现代电力，2010，27(4)：44-48．

[5]ZDORNOV V，BIRK Y．Battery and energy management in fleets of switchable battery EVs[J]．Innovative Smart Grid Technologies，2011(2)：1-7.

[6]张昌华，孟劲松，曹永兴，等．换电模式下电动汽车换电充裕度模型及仿真研究[J]．电网技术，2012，36(9)：15-19．

[7]TAYLOR M J，ALEXANDER A．Evaluation of the impact of plug-in electric vehicle loading on distribution system operations [C]//Proceedings of IEEE Power&Energy Society General Meeting．Calgary，Canada：IEEE，2009：1-6．

[8]VYAS A，SANTINI D．Use of national surveys for estimating full PHEV potential for oil use reduction[EB/OL]．[2012-11-06]. http://www.transportation.anl.gov/pdfs/HV/525.pdf.

[9]KRISTIEN C N，EDWIN H，JOHAN D．The impact of charging plug-in hybrid electric vehicles on a residential distribution grid [J]．IEEE Trans on Power Systems，2010，25(1)：371-380．

[10]田立亭，史双龙，贾卓．电动汽车充电功率需求的统计学建模方法[J]．电网技术，2010，34(11)：126-130．

Battery redundancy and charging equipment scale of battery swapping modes for electric vehicles

FU Yang1,QIU Yun1,ZHENG Zhi-min2,LI Wen-wei2
(1.Electric Power Engineering College,Shanghai University of Electric Power,Shanghai 200090,China;2.Ningbo Power Supply Bureau of Zhejiang Electric Power Corporation,Ningbo Zhejiang 315010,China)

Electric vehicle(EV)battery cost accounts for about one third cost of EVs.After the large-scale application of EV,it is of great significance to study the scale of charging equipment and the number of fully charged batteries in a battery swapping station in different time intervals for economical operation of swapping station and development of EV.The concept of battery redundancy was given,and a mathematical model based on certain EV owners'swapping demand and charging management strategy was proposed.The method was simulated by Monte Carlo method to get the reserved battery redundancy at different scales of charging equipment.The calculation results show that the method can drastically reduce battery redundancy on the initial growth stage of charging equipment scale. After arriving at corresponding scale,it also can contribute to the growth of coordinated charging capacity.

electric vehicle;battery swapping mode;charging equipment;battery redundancy;Monte Carlo method

TM 912

A

1002-087 X(2015)08-1715-04

2015-01-10

国家自然科学基金资助项目(51177098)；国家“863”计划(2012AA051704-4)；上海市重点科技攻关计划项目(11dz1210405)

符杨(1968—)，男，江苏省人，博士，教授，主要研究方向为城市电网规划、储能及电动汽车、风力发电及并网技术。