长春站非合作目标激光测距资料的定轨∗
孙建南刘承志 范存波 孙明国
(1中国科学院国家天文台长春人造卫星观测站长春130117)
(2中国科学院大学北京100049)
长春站非合作目标激光测距资料的定轨∗
孙建南1,2†刘承志1范存波1孙明国1
(1中国科学院国家天文台长春人造卫星观测站长春130117)
(2中国科学院大学北京100049)
精密解算了非合作目标的单站激光测距数据.观测数据少、数据弧段分布不好是对非合作目标进行精密定轨的难点.通过定轨过程中对动力学模型的选择及求解参数的选取,使得轨道计算收敛.解算多组圈数的非合作目标数据,将轨道重叠弧段对比作为评判定轨精度的指标;从多组圈数中提取出一圈的观测数据,对其余数据进行定轨处理,将定轨后的轨道结果与提取出的观测数据进行对比,得到在同一时刻的距离偏差,使其作为精密定轨的外符合.结果表明:对非合作目标(4814)进行精密定轨,平均测距残差为1.01 m,在测距方向上,测量数据外符合的平均轨道精度为14.35 m,预报1 d的测距精度为24.60 m.
航天器,天体力学:轨道计算与定轨,方法:数据分析
1 引言
利用漫反射激光测距对非合作目标进行探测,其测距精度可达米级或分米级,比雷达和光电观测精度高2∼3个数量级[1–3].高精度漫反射激光测距资料的应用对实现非合作目标精密定轨及其监测预警具有重要作用.同时有利于提高地球低轨道区域大气密度模型精度,进而对实现近地卫星精密定轨与预报、保障卫星顺利完成科学目标具有重要意义.
低轨非合作目标具有运行速度快、过境时间短、轨道预报精度差以及受到观测晨昏条件限制等特点,致使对其观测获得的有效激光测距数据远少于对合作目标观测获得的数据,导致在轨道改进计算中条件方程不可解,无法进行精密定轨.观测数据少已成为目前对非合作目标精密定轨的一个主要难点.文献[4−5]阐述了利用两行根数(Two-Line Element,TLE)数据模拟多站卫星激光测距(Satellite Laser Ranging,SLR)数据的方法实现单站SLR数据定轨,文章表明:对Ajisai卫星在1 d内拥有5圈共68个标准点的数据实施定轨,轨道外推5 d的位置误差在40 m以内.文献[6]基于文献[7]的方法,对轨道高度为800 km的空间目标在连续两天内拥有19个标准点的数据进行定轨,预报1 d的轨道精度可达20′′,优于利用光学数据预报的轨道精度.
本文首先介绍了SLR精密定轨的原理与方法及定轨过程中动力学模型的选取原则;其次,对长春站实测非合作目标的激光测距数据进行精密定轨.将TLE数据作为非合作目标精密定轨的初始轨道,选取适当的动力学模型与求解参数,使得轨道解算方程收敛;最后,通过重叠弧段比对和利用同类观测数据在距离方向上进行符合,分析定轨的精度.
2 SLR定轨原理与方法
SLR精密定轨采用动力学统计中基于线性估计的方法,利用含有测量误差的观测资料,依据动力学模型建立空间目标状态方程和观测方程,用动力学理论求解出目标状态参数的最佳估计值[8].
根据动力学理论,空间目标的状态方程可写为:

SLR的观测量是从观测站到卫星的距离,记为ρ0,其理论计算值为ρc.令Y=ρ0,G(X,t)=ρc,则空间目标的观测方程可写为:

式中,Xi、Yi、εi分别为ti时刻的状态、观测值以及观测噪声.
在参考状态X∗(t)处按Taylor公式展开状态方程(1)与观测方程(2),忽略2阶及以上的高阶项,得到观测方程为:
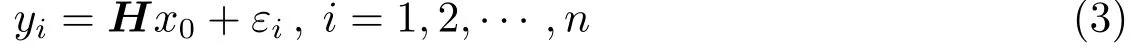

在求解估值过程中,一般采用迭代方法,直至满足设置的收敛准则为止.收敛准则为:①空间目标最新估值方差的位置矢量小于预先指定的判据POSmin.②观测残差的均方根满足:|RMS−RMSP|/RMS<δmin,RMS为观测残差的均方根,RMSP为观测残差均方根的线性预报值,δmin为预先指定的一个小量.若相继两次迭代满足条件①或条件②,则表示迭代过程已收敛.
在迭代计算中,需要依据卫星定轨精度σ以及定轨弧段的长短(t−t0)选取摄动加速度,即动力学模型.设卫星所受的摄动力为Fτ,卫星受到的地球中心引力为F0,对Fτ的量级EST通常采用下式来估计[9]:

设要考虑的Fτ的最小量级为estmin,那么

式中,to为轨道起算时刻,tf为终止时刻,n为卫星在轨道上运行的平均角速度.
3 非合作目标的精密定轨
3.1 定轨方案
现阶段长春人造卫星观测站成功实现了对400∼1800 km的非合作目标漫反射激光测距,目标的雷达散射截面(Radar Cross-Section,RCS)范围为1.2∼18.5 m2,观测共计244个目标466圈的数据,激光测距误差范围为0.3∼1.2 m,平均测距误差为0.9 m.通过www.space-track.org网站查询非合作目标的轨道高度,对文中实施定轨的非合作目标而言,平均轨道高度为550 km.根据平均测距残差值,取定轨精度为2 m,则σ=2.89×10−7,取弧长为4 d,那么,对耗散力而言,estmin=1.00×10−14;对保守力而言,estmin=3.82×10−10.根据这个标准,所选取的动力学模型如表1所示:

表1 动力学模型Table 1The perturbation dynamics models
在动力学定轨过程中,为了有效降低数学模型误差及吸收未模型化的误差,常把一部分的动力学参数作为待估计量,参与卫星状态参数解算中.解算参数的选择要在保证获得较高的定轨精度下设置,使所选参数之间保持弱相关性或不相关,以保证观测法方程的求解精度.综合考虑上述动力学模型后,对非合作目标的精密定轨方案如下:
(1)测量模型:大气折射模型选用Marini-Murray模型;台站位移的变化要考虑由固体潮、永久潮汐、海潮负荷以及地球自转形变对台站的影响.
(2)参考系:J2000.0惯性系;岁差选用IAU76模型;章动选用IAU1980模型;地球参考框架选择ITRF2000参考框架.
(3)本文所选的待估参数为:初始轨道的位置与速度,大气阻力系数.
3.2 数据处理
长春站在2014年3至5月对非合作目标进行了漫反射激光测距实验,对同1颗非合作目标拥有3圈以上观测弧段的数据做了部分统计,见图1.图中纵坐标为NORAD(North American Aerospace Defense Command)编号.
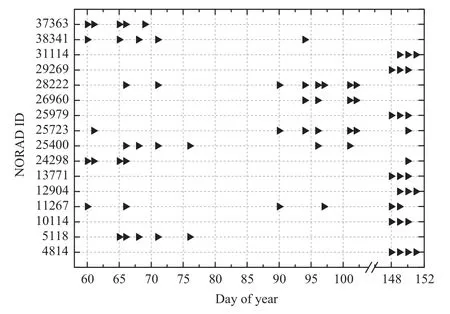
图1 2014年3至5月长春站漫反射激光测距观测非合作目标部分统计Fig.1 The partial data statistics of non-cooperative targets by the SLR based on di ff use reflection at Changchun station from 2014 March to May
从上图中选取出4组具有连续弧段的非合作目标数据(表2),分别实施精密定轨.由于非合作目标没有国际激光测距服务(International Laser Ranging Service,ILRS)提供的Consolidated Prediction Format(CPF)星历,不能获得较为精确的初始轨道信息.由文献[17–20]可知,使用Simplified General Perturbation Version 4(SGP4)模型计算TLE数据,对于近地轨道目标,轨道预报精度在百米量级,可作为非合作目标精密定轨的初始轨道.参数解算时,在整个弧段上求解初始轨道的位置、速度及大气阻力系数(对编号为4814、28222目标,需附加求解大气阻力系数的变化率).运用改良后采用数值方法的精密定轨软件解算非合作目标的Full-rate格式数据,设置迭代收敛判据POSmin为5 mm,δmin为0.01(见第2节).由于无法准确获取非合作目标形状特征,不能给出精确的质心改正值,但我们会依据定轨精度要求,并参考RCS值,对目标给出一定量的经验值进行质心修正.
采用上述定轨方案,对4颗非合作目标进行精密定轨后,在整个弧段上的内符合精度为1∼2 m(图2),符合激光漫反射测距残差范围.
3.3 精度评定
(1)重叠轨道弧段的符合程度常用来评价定轨结果的精度.对有连续4 d观测数据的非合作目标(4814),可以对前三天的观测数据进行定轨,生成轨道Orbit_1;对后三天的观测数据进行定轨,生成轨道Orbit_2;对连续4 d的观测数据进行定轨,生成轨道Orbit-3,计算重叠弧段在两天内的平均三维位置偏差与三维位置偏差的均方根误差.轨道Orbit-1与轨道Orbit-2之间计算出重叠轨道Overlap-1,轨道Orbit-2与轨道Orbit-3之间计算出重叠轨道Overlap-2,轨道Orbit-1与轨道Orbit-3之间计算出重叠轨道Overlap-3.通过重叠轨道弧段方法,得到重叠弧段上平均的最大三维位置偏差不超过80 m,其定轨精度在90 m以内(表3).

表2 非合作目标的激光漫反射测距信息Table 2 The information of non-cooperative targets by di ff use reflection laser ranging

表3 通过轨道重叠方法得到的轨道偏差Table 3 The orbit deviation obtained with the method of orbit overlap

图2 单站定轨后的测距残差Fig.2 The measurement residuals computed by precise orbit determination
(2)由于激光对非合作目标测距的误差在米级或分米级,在没有同等精度的外来轨道对非合作目标的定轨精度评价时,可利用同类激光观测数据评价轨道在测距方向上的精度.选取非合作目标(4814)其中3 d的激光漫反射测距数据,对其进行精密定轨,利用未参加轨道解算的观测数据进行测距符合,即对解算出的精密轨道,通过插值方法求得未参加轨道解算的观测数据在对应时间点的距离值,得到非合作目标轨道在测距方向上的偏差.
将5月28日、5月30日、5月31日3 d数据作为弧段Arc-1,将5月28日、5月29日、5月31日3 d数据作为弧段Arc-2,将5月28日、5月29日、5月30日3 d数据作为弧段Arc-3,分别实施精密定轨,得到定轨后的平均测距残差为0.95 m(表4).在精密定轨过程中,解算参数为初始轨道的位置与速度和大气阻力系数.
利用弧段Arc-1的精密定轨结果符合5月29日的观测数据,平均测距误差为11.35 m,均方根值为13.62 m.利用弧段Arc-2的精密定轨结果符合5月30日的观测数据,平均测距误差为−17.32 m,均方根值为17.35 m(图3).对弧段Arc-3精密定轨后,进行24 h轨道预报,将轨道结果与5月31日的观测数据进行符合,平均测距误差为24.60 m,均方根值为56.10 m(图4).

表4 各个弧段精密定轨的测距残差Table 4 The measurement residuals calculated by precise orbit determination of each arc segment

图3 观测数据外符合的精度Fig.3 The precision of orbit determination coincided with the SLR data

图4 预报1 d的轨道精度Fig.4 The precision of 1-day orbit prediction
4 结论与讨论
对长春站在2014年3至5月实测的部分非合作目标进行了精密定轨,得到内符合精度范围为1∼2 m.通过轨道弧段重叠比对可得到非合作目标数据精密定轨的精度.对非合作目标(4814)进行精密定轨,在连续两天的重叠弧段内,平均最大三维位置偏差不超过80 m,精密定轨精度好于90 m.由于目前还没有同等精度的外来轨道对非合作目标的轨道进行符合,尤其是针对空间碎片数据的定轨,可利用同类观测数据对精密定轨结果进行测距方向的符合.结果表明,非合作目标(4814)在距离方向上平均定轨精度为14.35 m,预报1 d的测距精度为24.60 m.
本文利用长春人造卫星观测站短弧激光漫反射测距数据实现了非合作目标(4814、12904、28222和37363)的精密定轨,具体分析了非合作目标(4814)的定轨结果,定轨精度优于百米.使用SGP4模型计算TLE数据作为精密定轨的初始轨道,通过动力学模型的选取及求解参数的选择,使得非合作目标的定轨程序解算收敛.若使用光学数据、雷达数据、TLE数据共同参与激光漫反射测距数据的解算中,更有助于提高轨道解算的收敛性.倘若增加多个台站对同一颗非合作目标的观测,则可获得非合作目标更高的轨道精度与预报信息,在不断提高非合作目标的预报精度时,可实现激光漫反射测距的良性循环观测,对空间非合作目标监测预警具有重要的应用价值.
致谢感谢长春人造卫星观测站激光测距组全体职员为本文提供的数据支持
[1]李语强,李祝莲,伏红林,等.中国激光,2011,38:154
[2]Kirchner G,Koidl F,Friederich F,et al.AdSpR,2013,51:21
[3]Bennett J C,Sang J,Smith C H,et al.AdSpR,2013,52:1876
[4]梁智鹏,刘承志,范存波,等.天文学报,2012,53:137
[5]Liang Z P,Liu C Z,Fan C B,et al.ChA&A,2012,36:417
[6]Bennett J C,Sang J,Smith C,et al.Improving Low-Earth Orbit Predictions Using Two-line Element Data with Bias Correction.Advanced Maui Optical and Space Surveillance Technologies Conference, 2012:12-14
[7]Levit C,Marshall W.AdSpR,2011,47:1107
[8]Schutz B,Tapley B,Born G H.Statistical Orbit Determination.New York:Academic Press,2004: 1-10
[9]刘林.人造地球卫星轨道力学.北京:高等教育出版社,1992:102-103
[10]Tapley B,Ries J,Bettadpur S,et al.JGeod,2005,79:467
[11]Standish E M.BAAS,1995,27:1203
[12]Berger C,Biancale R,Ill M,et al.JGeod,1998,72:161
[13]Eanes R J,Watkins M M.ITN,1994,17:118
[14]Ray R D.A Global Ocean Tide Model from Topex/Poseidon Altimetry:GOT99.2.NASA Tech.Memo. 209478,Goddard Space Flight Center,Greenbelt
[15]Sengoku A,Cheng M K,Schutz B E.JGeod,1995,70:140
[16]Pavlis D E,Luo S,Dahiroc P,et al.Hughes STX Contractor Report,1998
[17]韩蕾,陈磊,周伯昭.中国空间科学技术,2005,24:65
[18]韦栋,赵长印.天文学报,2009,50:332
[19]Wei D,Zhao C Y.ChA&A,2010,34:69
[20]刘卫,缪元兴.天文研究与技术,2011,8:128
Orbit Determination of Non-cooperative Targets Using Laser Ranging Data at Changchun Station
SUN Jian-nan1,2LIU Cheng-zhi1FAN Cun-bo1SUN Ming-guo1
(1 Changchun Observatory,National Astronomical Observatories,Chinese Academy of Sciences, Changchun 130117)
(2 University of Chinese Academy of Sciences,Beijing 100049)
The precise orbit determination software successfully processes the satellite laser ranging data of the non-cooperative targets in a single station.The insufficient observation data and the sole distribution data have become a principal difficulty in the orbit determination of the non-cooperative targets.Through the choices of dynamic models and the selections of solving parameters in the process of orbit determination, the condition equation can be solved with a convergence algorithm,and the orbit is obtained.The positional deviation obtained with the method of orbital overlap will be used as the accuracy index in calculating more groups of non-cooperative targets data.And the ranging deviation is obtained by comparing the trajectory information after orbit determination with the observation data uninvolved in orbit determination, which can be regarded as the externally coincident precision.The results show that the average ranging residual is 1.01 meters,the outer precision is 14.35 meters,and the precision of 1-day orbit prediction is 24.60 meters for non-cooperative target(4814).
space vehicles,celestial mechanics:orbit calculation and determination, methods:data analysis
P135;
A
10.15940/j.cnki.0001-5245.2015.05.007
2015-01-22收到原稿,2015-04-16收到修改稿
∗国家自然科学基金项目(11373047)资助
†sunjn@cho.ac.cn

