可穿透腔体外有障碍物的正散射问题

彭超权，陶 婷

(中南民族大学 数学与统计学学院,武汉 430074)

可穿透腔体外有障碍物的正散射问题

彭超权，陶 婷

(中南民族大学 数学与统计学学院,武汉 430074)

分析了用点源作为入射波，散射体由一个可穿透腔体和一个外部不可穿透的障碍物组成的正散射问题，指出了该问题可归结为对具有一定边界条件的Helmholtz方程的求解. 通过边界积分方程的方法, 利用位势理论和Fredholm定理，证明了该问题解的存在性和唯一性.

边界积分方程的方法；Helmholtz方程；Fredholm定理；可穿透腔体

1 主要问题及结果

(1)

其中正常数k1，k0分别是区域D1和D内的波数，ν为外单位的法向量，λ1和λ2为正常数，总场u=ui+us，ui=Φ1(·,z)，z∈D1, 其中Φ1(·，z)为Helmholtz方程的基本解, 定义如下:

通常的散射问题可用有界障碍物外的无界区域的Helmholtz方程来刻画[1,2]. 近年来, 有关腔体的内散射问题受到了一定的关注. 2010年, Qin和Colton在文[3]中利用腔体内部的点源和测量值研究了确定腔体的反散射问题. 更多关于腔体的正反散射问题，可参考文[4],[5]. 然而可穿透腔体外部有障碍物的情形却很少有文献涉及，本文借助于文献[6]中的想法和技术来研究问题 (1). 我们将在适当的函数空间中，利用边界积分方程的方法将问题 (2) 转化成一个边界积分系统， 并证明积分算子的Fredholm性质和单射性，从而得到问题的解的存在唯一性.

(2)

注意问题(1)是问题(2)的特殊情况.文章主要结论为以下两个定理.

定理1 混合边界问题(2)的解至多只有一个.

定理2 问题(2)具有唯一解，它满足下列估计:

2 预备知识

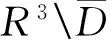
定理4(Green公式) 设Ω是一个多连通区域，其边界为Γ，令w(x,y)和v(x,y)在其边界Γ上具有二阶连续偏导数，则我们有格林第一恒等式：

和格林第二恒等式：

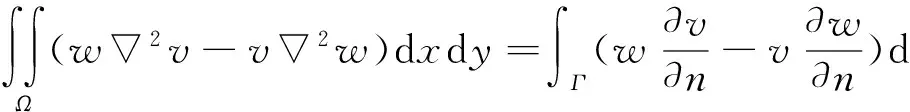
定理5 (Fredholm定理) 设X是一个赋范空间，A:X|→X是一个线性紧算子，若齐次方程：

(I+A)φ=0,

只有零解，则对任意的f∈X非齐次方程：

(I+A)φ=f,

有唯一解φ∈X，并且解连续依赖于f.

的散射解，并且在边界∂D上满足：

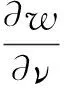
那么在R3D上w≡0.

3 定理1的证明

根据问题(2)中的边界条件有：

由于k0,k1,λ1,λ2均为正实数，所以可得：

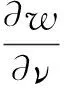
由定理6可知在D1中w≡0, 即证.

4 定理2的证明

引理1 积分方程 (12) 是一个第二类的Fredholm积分算子.

证明 假设问题(2)具有以下形式的解：

Φ0(x,y)φ(y)}ds(y),x∈D1,

(3)

(4)

下面我们根据单双层位势的性质，推导出w,v所满足的边界条件. 利用单层位势在边界处的跳跃关系，当x从D1的内部趋向于边界∂D1时，将其限制在∂D1，可得：

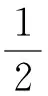
(5)

当x从D1的外部趋向于边界∂D1时，可得：

(6)

联立(5),(6)式得：

化简即为：

ψ(x)-m(λ1K11,0-K11,1)Ψ(x)-m(S11,0-S11,1)φ(x)+m(S12,1+iηK12,1S2)φ(x)=-mfon ∂D1.

(7)

当x从D1的内部趋向于边界∂D1时，将其限制在∂D1上，可得：

(8)

当x从D1的外部趋向于边界∂D1时，我们有：

首先，要求国家立法机关制定或修改相应的社会保障法律，将农业劳动者纳入到现行的社会保险体系中来，真正建设统筹城乡的社会保障体系。现行的社会保险法主要以职工为核心建立起来，实际上并不重视几亿农业劳动者的医疗、养老问题，这是我国农村资源和资金分配地位的具体表现。所以，在立法上重构社会保险法成为最关键课题。

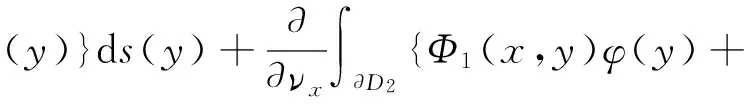
(9)

(10)

(Tij,hφ)(x)=

由v(x)在D2上的跳跃关系，当x从D2的外部趋向于∂D2的边界，并将其限制在∂D2上，同理也可得：

(11)

那么联合 (7)，(10)，(11)式，我们得到如下的边界积分系统：

(I+A)U=R.

(12)

其中I是恒等算子. 若我们能够求解出唯一的解U=(ψ,φ,φ)T，则问题(2)就有形如(3)，(4)式的唯一解.

引理2 边界积分方程(12)存在唯一的解.

证明 根据定理5，由于A的紧性，我们只需证明齐次算子方程：

(I+A)U=0.

(13)

只有零解，便可得(I+A)U=R存在唯一性的解.令R=0，则此时w，v是问题(2)的具有齐次边界条件的解，由定理1知：

w=0,x∈D1,
v=0,x∈D.

我们也可以将v定义在D2内，且v满足：

由跳跃条件：

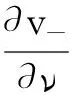
根据格林恒等式有：

可知Sφ=0,x∈∂D1.以上积分函数在无穷远处和∂D2上恒为0，由调和函数的极值原理可知S在R3恒为0，从而由跳跃条件：

(14)

Φ1(x,y)φ(y)}ds(y),x∈D1.

(15)

由单双层位势的跳跃关系得:

(16)

故ψ,φ,φ都为0，从而(I+A)U=0只有零解. 故算子I+A也是单射. 由Freholm定理，I+A逆算子(I+A)-1存在且有界. 所以积分方程 (12) 存在唯一的解.

定理2的证明 由引理2的结论知I+A的逆算子(I+A)-1是存在且有界的，再利用位势函数 (3)，(4)可得.

[1] Colton D,Kress R.Integral equation methods in scattering theory [M]. New York： Wiley,1983:1-271.

[2] Hsiao G C, Wendland W L. Boundary integral equations[J]. Applied Mathematical Sciences， 2013,76(4):509-547.

[3] Qin H H, Colton D. The inverse scattering problem for cavities[J]. Applied Numerical Mathematicals, 2012,62 (2):699-708.

[4] Liu X. The factorization method for cavities[J]. Inverse Problem, 2014,30 (1):015006.

[5] Meng S, Haddar H, Cakoni F. The factorization method for cavity in an inhomogeneous medium[J]. Inverse Problem, 2014,30 (4): 045008.

[6] Liu X, Zhang B. Direct and inverse obstacle scattering problems in a piecewise homogeneous medium[J]. SIAM Journal on Applied Mathematics, 2010,70 (8):3105-3120.

Direct Scattering Problem for A Penetrable Cavity and An External Obstacle

PengChaoquan,TaoTing

(College of Mathematics and Statistics,South-Central University for Nationalities, Wuhan 430074,China)

By using a point source as the incident wave,we consider the scattering problem by a mixed scatterer which is composed of a penetrable cavity and an external impenetrable obstacle, and regard that this problem comes down to solving the Helmholtz equation with certain boundary conditions. By using the boundary integral equation method and based on the Fredholm theorem,we prove that the scattering problem has a unique solution in the form of combined potentials.

boundary integral equation method; Helmholtz equation; Fredholm theorem;a penetrable cavity

2015-05-25

彭超权(1979-)，男，副教授，博士，研究方向：偏微分方程，E-mail：pcq1979@163.com

中南民族大学研究生创新基金资助项目(2015sycxjj125)

O175.25

A

1672-4321(2015)03-0118-05