基于混沌蚁群算法的弹性阻抗反演

张 进,安振芳,邢 磊,安玲芳,赵 玺,陈晓琦

(中国海洋大学海洋地球科学学院,山东青岛266100)

基于混沌蚁群算法的弹性阻抗反演

张 进,安振芳,邢 磊,安玲芳,赵 玺,陈晓琦

(中国海洋大学海洋地球科学学院,山东青岛266100)

弹性阻抗反演属于叠前反演,能够反映振幅随偏移距或入射角的变化,可以获得纵波速度、横波速度、密度、泊松比以及拉梅系数等多种岩性参数。目前,弹性阻抗反演的常规算法为广义线性反演,该反演方法强烈依赖初始模型,容易陷入局部极小。为此,尝试将一种优秀的非线性算法——混沌蚁群算法应用于弹性阻抗反演中,该算法具有能达到全局最小,不依赖初始模型等优点。模型测试证明了混沌蚁群算法的稳定性和可靠性。将基于混沌蚁群的弹性阻抗反演方法应用于胜利油田某储层,其反演结果与实际钻探及测井解释相一致,验证了该反演方法的可行性和有效性。

弹性阻抗；非线性反演；混沌蚁群算法

弹性阻抗反演属于叠前反演的范畴,是声波阻抗与AVO技术的结合,因此弹性阻抗反演可反映振幅随偏移距变化的信息,具有良好的保真性和多信息性。与AVO相比,弹性阻抗反演中子波的提取不受角度限制,还有助于确定剩余NMO校正,所以弹性阻抗反演比AVO更鲁棒。由弹性阻抗反演数据体可获得纵、横波阻抗,纵、横波速度,纵横波速度比,密度,泊松比以及拉梅系数等多种参数体,比叠后波阻抗反演更能反映地层岩性和流体特征,进而更可靠地揭示地下储层的空间展布情况和岩石物性及含油气性[1]。

1999年,Connolly[2]首次引入弹性阻抗(Elastic Impedance,EI)概念,并将其用于岩性识别和流体预测。2000年,Cambois[3]对AVO反演和EI反演进行了比较,认为这两种方法只有在子波不随偏移距变化时才是相同的。2001年,Mallick[4]对Connolly弹性阻抗公式的应用条件进行了讨论。2002年,Whitcombe[5]对Connolly提出的弹性阻抗进行了归一化。2003年,倪逸[6]提出了一种基于范数动态可调的弹性阻抗计算方法。2003—2004年，马劲风[7-8]分别提出了广义弹性阻抗(Generalized Elastic Impedance,GEI)、反射率阻抗(Reflectivity Impedance,RI)和射线弹性阻抗(Ray-path Elastic Impedance,REI)概念。2006年,Quakenbush等[9]提出了泊松比阻抗(Poisson Impedance,PI)。随后,王保丽等[10-11]提出了基于Gray近似与Fatti近似的弹性阻抗公式。经过近十年的研究与发展,弹性阻抗反演技术日臻完善,在国内外各大油田中的实际应用效果明显[12-16]。

弹性阻抗反演本质上为典型的非线性参数估计问题。常规的反演方法,如约束稀疏脉冲反演(Constrained Sparse Spike Inversion,CSSI),通常是把非线性问题线性化,解的稳定性受初始模型的影响较大,且容易陷入局部极小。因此必须寻求一种完全非线性优化算法来求解地球物理中的反问题。

蚁群算法由Dorigo等人首先提出,即蚂蚁系统(Ant System,AS),并成功应用于求解旅行商问题(Traveling Salesman Problem,TSP)[17-19]。该算法的问世引起了普遍关注和研究,针对AS算法的缺点,提出了许多改进的蚁群算法,如本文采用的混沌蚁群算法等[20-22]。蚁群算法不仅克服了传统优化算法容易陷入局部极优的缺点,而且还提高了搜索精度和搜索效率。鉴于此,近年来有些学者将其应用到其它领域,并取得了很好的应用效果[23-25]。为了求解地球物理中的反问题,我们将混沌蚁群算法应用于弹性阻抗反演。具体做法为:首先将目标函数中的反射系数序列进行合理编码,以映射为离散域优化问题。然后仿照AS算法的思想对最优解进行搜索。在搜索过程中,为了提高收敛速度及解的质量,每一次循环过程中都加入混沌算子,在当前最优值附近进行混沌搜索。若搜索到的新值优于当前最优值,则替换掉当前最优值,直至得到最终结果。最后我们将该弹性阻抗反演方法应用于胜利油田某储层,其反演结果与实际钻探及测井解释相一致。

1 弹性阻抗反演的基本原理

Connolly[2]根据Zoeppritz方程的三项Aki-Richards简化公式推导出与角度有关的弹性阻抗表达式为:

(1)

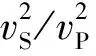
根据声波阻抗与反射系数的关系而构建的弹性阻抗与反射系数的关系表达式为:

(2)

仿照声波阻抗(AI)递推反演,得出弹性阻抗反演递推公式为:

(3)

在没有噪声的情况下,用与角度有关的数据表示的褶积模型为:

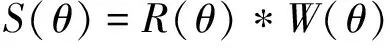
(4)

式中:S(θ)为角度地震道；R(θ)为角度反射系数；W(θ)为角度子波。

在弹性阻抗反演之前需要分别对地震资料和测井资料进行处理。地震资料的特点是纵向分辨率低、横向密集；而测井资料的特点是纵向分辨率高、横向稀疏。弹性阻抗反演就是将二者的优势结合起来,以富含地下地质信息的地震资料为主,以测井资料作为约束,进行地震与测井联合反演。

弹性阻抗反演的基本步骤主要包括[1]:①地震资料处理；②测井资料处理；③建立低频模型；④提取角度子波。其中,第2)步需要利用测井获得的纵波速度、横波速度和密度以及地震数据提供的角度,根据公式(1)计算出井旁道弹性阻抗IE(θ)伪测井曲线。第④步需要根据公式(4)从角道集数据体中提取角度子波,提取角度子波需要满足的条件为:

(5)

式中:E为误差能量；d为井旁地震记录；s=r*w为合成地震记录；r为反射系数；w为提取的子波。提取的最佳子波就是使误差能量E最小的子波。

利用弹性阻抗反演获得的弹性阻抗数据体,再根据公式(6)进行岩性参数的提取,即可得到纵波速度、横波速度和密度等基本岩性参数。通过参数之间的相互关系进行计算还可以得到泊松比、拉梅系数以及剪切模量等岩性参数。

(6)

2 混沌蚁群算法的基本原理

混沌蚁群算法的核心思想是:蚂蚁在外出觅食过程中,如何利用混沌搜索原理以及信息素的释放与挥发机制,在最短时间内建立起巢穴和食物源之间的最短路径。假设在以巢穴N为中心,以R为半径的一定空间范围内有一食物源F,有m只蚂蚁同时爬出巢穴寻找食物。由于刚开始谁也不知道食物源位置,只好分头行动各自为营,在找到食物源以前,每只蚂蚁的行为都是混沌的。由于混沌的遍历性特点,很快其中的一只蚂蚁k最先发现了食物源。因在速度相同的情况下蚂蚁k用时最短,故蚂蚁k所走路径即为最短路径。蚂蚁在觅食过程中会释放出一种信息素,它们会根据信息素的多少来选择行走的路径,研究表明蚂蚁更倾向于走信息素多的路径。而信息素的多少与路径的长短有关,因为信息素会随着时间的流逝而挥发,且在速度相同的情况下单位时间内短路径上通过的蚂蚁多,于是短路径上的信息素越来越多,这就意味着越来越多的蚂蚁选择短路径,这样就形成了一种正反馈机制,直到所有的蚂蚁都选择最短路径为止[17]。

最初的蚁群算法用于解决TSP问题,因为蚁群觅食的过程与TSP的求解非常相似,下面以TSP为例,介绍混沌蚁群算法[26-28]。

2.1 自变量的编码

本文采用陈烨[29]提出的“十进制编码”方式将待优化函数的自变量表示为一串十进制数字串{d(0),d(1),d(2),…,d(l-1)},而自变量可以通过如下解码公式解码得到:

(7)

解码公式所表示的过程可以用图1来形象地描述。图1两端的黑色圆点分别代表蚂蚁搜索的起点与终点,每一列数字视作一个隔层,起点和终点之间共有8个隔层,每层有10个城市,蚂蚁从起点到终点的搜索过程中,必须依次经过所有隔层,中间不允许跳过任何一层。

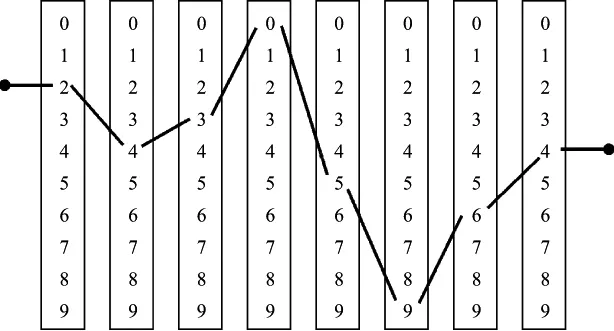
图1 蚂蚁搜索路径示意

2.2 状态转移规则

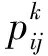
(8)

式中：dk=(0,1,…,n-1)表示蚂蚁k下一步允许选择的城市。

2.3 信息素更新规则

如果残留信息不被及时更新就会影响启发信息,t+n时刻在路径(i,j)上的信息可根据公式(9)和公式(10)进行调整:

(9)

(10)

2.4 混沌算子的嵌入

基本蚁群算法虽然具有较强的鲁棒性和发现较好解的能力,但是也存在搜索时间过长、易于停滞的问题。为了提高收敛速度及解的质量,每一次循环过程中都加入混沌算子。混沌模型有很多种,目前通常用Logistic映射产生混沌序列:

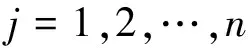
(11)

式中:u为常数,一般取值范围为[3.56,4.00]。当u=4.00,Zj∈(0,1)且不等于0.25,0.50,0.75时,将产生混沌现象,Zj会在(0,1)遍历。

3 利用混沌蚁群算法进行弹性阻抗反演

本文利用混沌蚁群算法对弹性阻抗进行反演,其所要求的目标函数为:

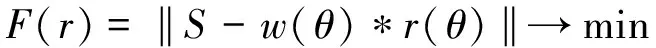
(12)

式中:F(r)为误差函数；S为角道集；w(θ)为角度子波；r(θ)为要求的角度反射系数序列。由(12)式可知,反演出的角度反射系数r(θ)必须满足使误差函数F(r)最小的条件。

基于混沌蚁群算法的弹性阻抗反演流程(图2)如下。

1) 根据公式(4)和公式(5)提取角度子波。

2) 对要求的反射系数序列r(θ)进行编码。

3) 根据公式(8)选择下一个城市。

4) 根据公式(9)和公式(10)对残留信息素进行更新处理。

5) 每只蚂蚁构造出一条路径后,由公式(7)对自变量进行解码并计算其函数值。筛选出迭代最优蚂蚁,若它比全局最优蚂蚁还好,则将其设置为全局最优蚂蚁。

6) 在全局最优蚂蚁附近进行混沌搜索,若搜索到的解比全局最优蚂蚁更好,则将其替换成全局最优蚂蚁。

7) 根据公式(12)计算误差函数F(r)。

8) 循环迭代,对最优解不断进行优化,直到满足终止条件。

9) 根据公式(7)对最优路径上的城市进行解码,解码后的值即为要求的各个反射系数值。

图3a是利用5°角道集反演出的反射系数与真实反射系数对比；图3b为计算出的地震记录与实际地震记录的对比。可以看出,反演结果与实际数据吻合得很好。

采用同样的方法求取其他角度道集的反射系数,然后根据第一层的弹性阻抗值IE0,即可得到各角度的弹性阻抗值。其中5°,25°和45°角道集反演出的弹性阻抗曲线如图4所示。

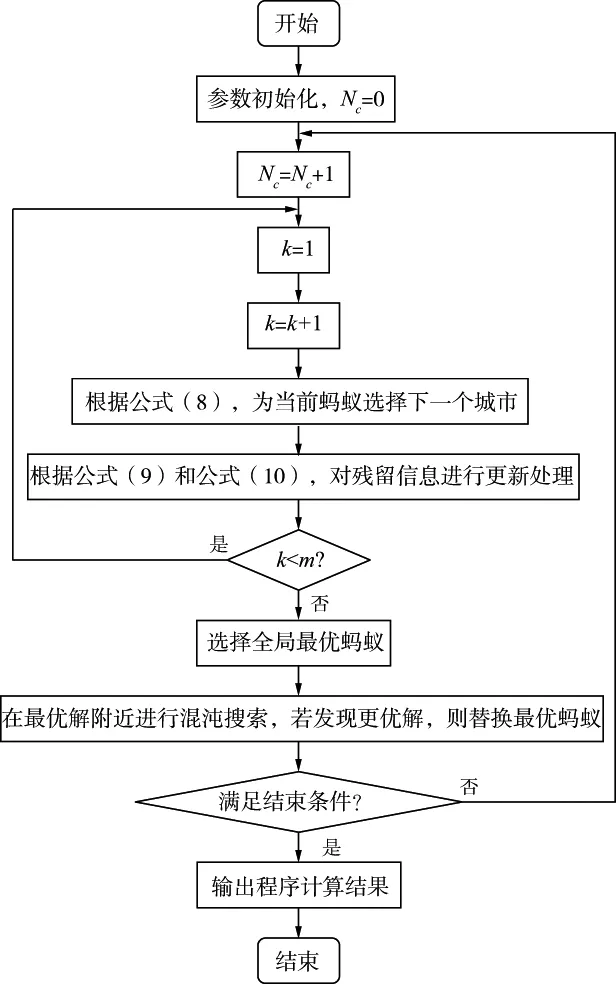
图2 基于混沌蚁群算法的弹性阻抗反演流程

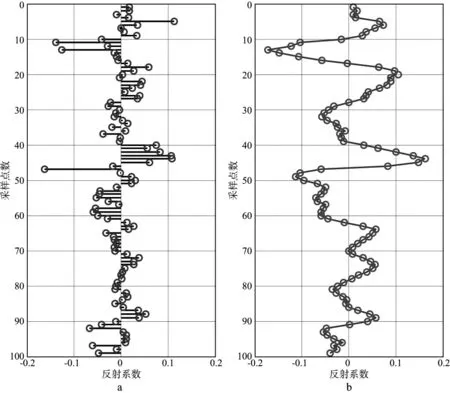
图3 利用5°角道集反演的反射系数(圆圈)与真实的反射系数(实线)对比(a)；合成地震记录(圆圈)与实际地震记录(实线)对比(b)

图4 5°,25°和45°角道集反演出的弹性阻抗曲线

采用部分实际测井曲线对反演方法进行测试,总共有100个采样点,采样间隔是1ms。图5给出了反演结果和实际测井曲线的对比。其中图5a,图5b和图5c中的红虚线表示原始P波速度、原始S波速度和密度测井曲线；图5c和图5d中的红虚线表示伪P波阻抗(lP)和伪S波阻抗(lS),它们依据原始P波速度、S波速度和密度数据计算所得。图5中的蓝实线为反演出的P波速度、S波速度、密度、P波阻抗和S波阻抗。可以看出,反演出的各弹性参数曲线与原测井曲线吻合得很好。

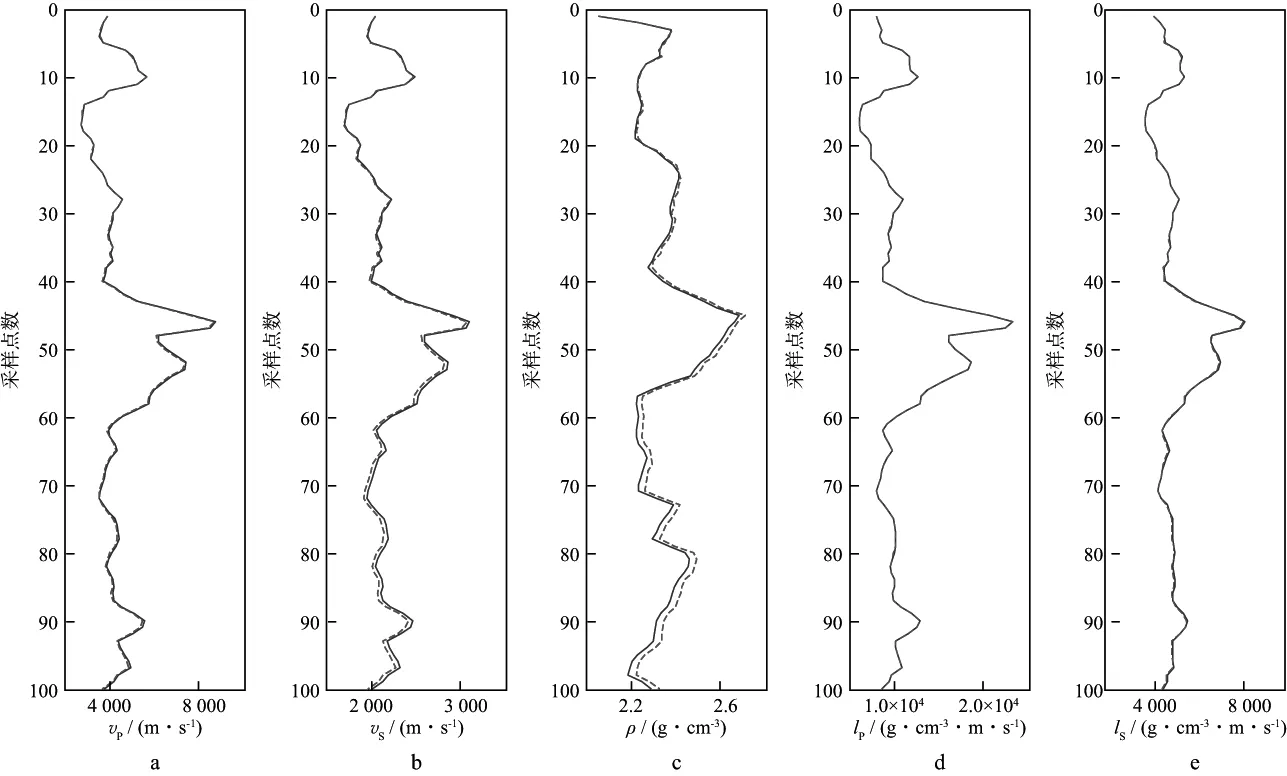
图5 反演结果(蓝实线)与测井曲线(红虚线)对比

4 应用实例

我们选择胜利油田某储层部分2D地震数据来测试本文反演方法。在弹性阻抗反演之前需要进行一系列振幅保持处理,比如球面扩散补偿、地表一致性反褶积、随机噪声衰减、反Q滤波和叠前时间偏移等,以确保最终叠前振幅能够精确表示地下界面的反射强度。然后将预处理的偏移距数据体转换成角道集数据体,从中抽取5°,15°和25°的角道集,并提取与之相应的角度子波。最后我们用混沌蚁群算法对处理好的实际数据进行弹性阻抗反演,得到了多种反映岩性和流体变化的属性剖面,反演出的λρ，μρ和vP/vS剖面如图6至图8所示。

为了验证本文提出的反演方法的可行性和有效性,我们抽取的测线穿过GS1井(CDP 377),储层位于井深约2890m(2398ms)处。对GS1井的测井资料进行分析,我们发现与周围泥岩相比含油砂岩的μρ相对较高,而λρ和vP/vS则相对较低。从图6至图8中可以看出,用混沌蚁群算法反演出的属性剖面与GS1井的实际钻探及测井解释结果相一致(如图中用白色椭圆所圈出的位置)。表明了混沌蚁群算法不仅搜索精度高而且稳定性能好,体现了弹性阻抗反演在寻找油气资源方面的巨大潜力。

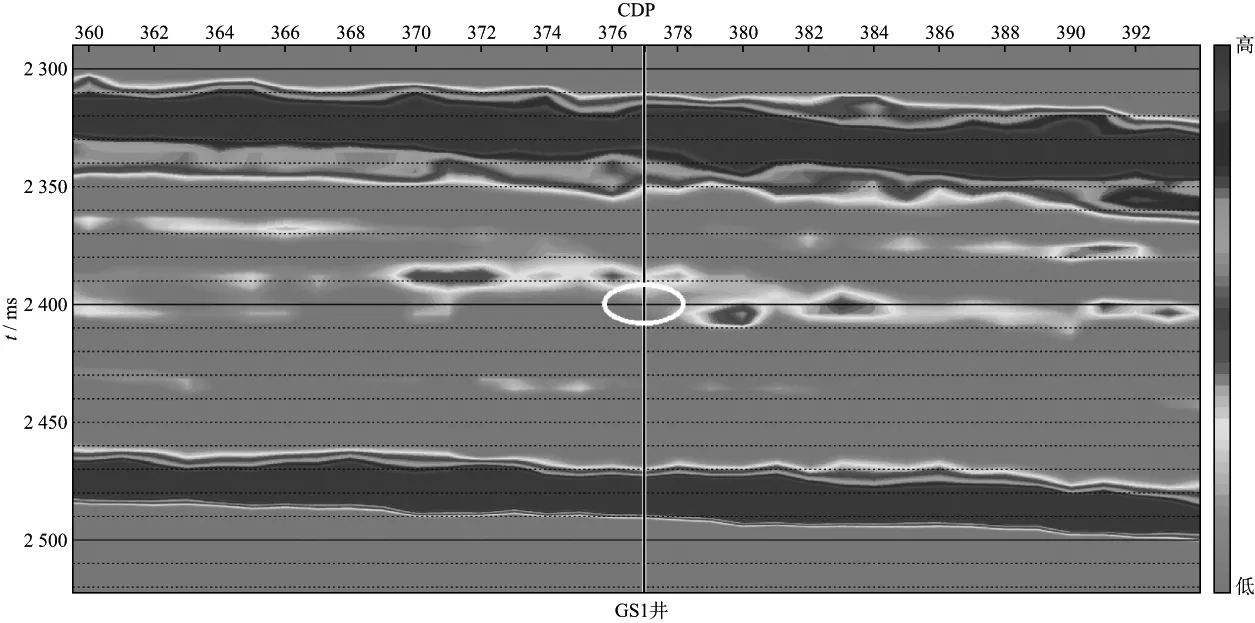
图6 过GS1井(CDP 377)的λρ剖面(椭圆所圈位置即是预测储层位置)

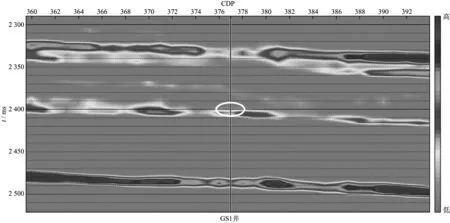
图7 过GS1井(CDP 377)的μρ剖面(椭圆所圈位置即是预测储层位置)

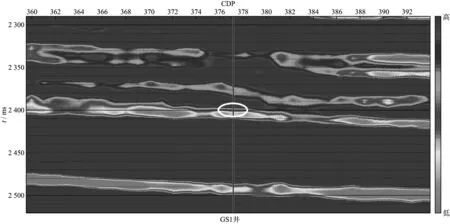
图8 过GS1井(CDP 377)的vP/vS剖面(椭圆所圈位置即是预测储层位置)

5 结论

本文提出了基于混沌蚁群算法的弹性阻抗反演方法,经模型测试和实际资料的应用分析后得出以下认识:

1) 基于混沌蚁群算法的弹性阻抗反演方法具有不依赖于初始模型,避免陷入局部极小值的优点,能够在较短时间内搜索到全局最优解。模型测试证明了将混沌蚁群算法应用于弹性阻抗反演的可行性和有效性。

2) 本文将基于混沌蚁群算法的弹性阻抗反演方法应用于胜利油田某储层的叠前地震数据,得到了λρ，μρ和vP/vS岩性参数剖面,与测井解释结果相一致。表明本文基于混沌蚁群算法的弹性阻抗非线性反演方法切实可行,具有良好的发展潜力和应用前景,为油气藏属性分析和预测提供了一条新的途径。

[1] 王保丽,印兴耀,张繁昌.弹性阻抗反演及应用研究[J].地球物理学进展,2005,20(1):89-92 Wang B L,Yin X Y,Zhang F C.Elastic impedance inversion and its application[J].Progress in Geophysics,2005,20(1):89-92

[2] Connolly P.Elastic impedance[J].The Leading Edge,1999,18(4):438-452

[3] Cambois G.AVO inversion and elastic impedance[J].Expanded Abstracts of 70thAnnual Internat SEG Mtg,2000,142-145

[4] Mallick S.AVO and elastic impedance[J].The Leading Edge,2001,20(10):1094-1104

[5] Whitcombe D N.Elastic impedance normalization[J].Geophysics,2002,67(1):60-62

[6] 倪逸.弹性波阻抗计算的一种新方法[J].石油地球物理勘探,2003,38(2):147-150,155 Ni Y.A new method for calculation of elastic wave impedance[J].Oil Geophysical Prospecting,2003,38(2):147-150,155

[7] 马劲风.地震勘探中广义弹性阻抗的正反演[J].地球物理学报,2003,46(1):118-124 Ma J F.Forward modeling and inversion method of generalized elastic impedance in seismic exploration[J].Chinese Journal of Geophysics,2003,46(1):118-124

[8] Ma J F,Morozov I B.Ray-path elastic impedance[J].CSEG National Convention,2004,10-12

[9] Quakenbush M,Shang B,Tuttle C.Poisson impedance[J].The Leading Edge,2006,25(2):126-128

[10] 王保丽,印兴耀,张繁昌.基于Gray近似的弹性波阻抗方程及反演[J].石油地球物理勘探,2007,42(4):435-439 Wang B L,Yin X Y,Zhang F C.Gray approximation based elastic wave impedance equation and inversion[J].Oil Geophysical Prospecting,2007,42(4):435-439

[11] 王保丽,印兴耀,张繁昌,等.基于Fatti近似的弹性阻抗方程及反演[J].地球物理学进展,2008,23(1):192-197 Wang B L,Yin X Y,Zhang F C,et al.Elastic impedance equation based on Fatti approximation and inversion[J].Progress in Geophysics,2008,23(1):192-197

[12] Lu S M,McMechan G A.Elastic impedance inversion of multichannel seismic data from unconsolidated sediments containing gas hydrate and free gas[J].Geophysics,2004,69(1):164-179

[13] 刘国萍,陈小宏,李景叶.弹性波阻抗在时移地震中的应用分析[J].地球物理学进展,2006,21(2):559-563 Liu G P,Chen X H,Li J Y.Application and analysis of elastic impedance in time-lapse seismology[J].Progress in Goephysics,2006,21(2):559-563

[14] 孙翠娟,张文,刘志斌.弹性波阻抗反演技术在辽东湾隐蔽油气藏勘探中的应用[J].中国海上油气,2007,19(3):162-165,172 Sun C J,Zhang W,Liu Z B.An application of the elastic impedance inversion technique to exploration of subtle reservoirs in Liaodong gulf[J].China Offshore Oil and Gas,2007,19(3):162-165,172

[15] 畅永刚,张宗和,王志美,等.弹性阻抗反演在火山岩发育区应用效果分析——以冀东滩海地区南堡构造为例[J].天然气地球科学,2007,18(3):422-425 Chang Y G,Zhang Z H,Wang Z M,et al.Application effects of elastic impedance seismic trace inversion in igneous strata[J].Natural Gas Geoscience,2007,18(3):422-425

[16] 彭真明,李亚林,巫盛洪,等.碳酸盐岩储层多角度弹性阻抗流体识别方法[J].地球物理学报,2008,51(3):881-885 Peng Z M,Li Y L,Wu S H,et al.Discriminating gas and water using multi-angle extended elastic impedance inversion in carbonate reservoirs[J].Chinese Journal of Geophysics,2008,51(3):881-885

[17] Colorni A,Dorigo M,Maniezzo V,et al.Distributed optimization by ant colonies[J].Proceedings of European Conference on Artificial Life,1991,134-142

[18] Dorigo M,Maniezzo V,Colorni A.Ant system:optimization by a colony of cooperating agents[J].IEEE Transactions on Systems,Man,and Cybernetics(Part B),1996,26(1):29-41

[19] Dorigo M,Gambardella L M.Ant colony system:a cooperative learning approach to the traveling salesman problem[J].IEEE Transactions on Evolutionary Computaion,1997,1(1):53-66

[20] 高尚.解旅行商问题的混沌蚁群算法[J].系统工程理论与实践,2005,25(9):100-104,125 Gao S.Solving traveling salesman problem by chaos ant colony optimization algorithm[J].Systems Engineering-Theory and Practice,2005,25(9):100-104,125

[21] 陈烨.变尺度混沌蚁群优化算法[J].计算机工程与应用,2007,43(3):68-70 Chen Y.Scaleable chaotic ant colony optimization[J].Computer Engineering and Applications,2007,43(3):68-70

[22] 袁冬根,刘晓东,蔡磊,等.基于混沌蚁群算法的BP神经网络训练研究[J].微电子学与计算机,2009,26(4):11-14 Yuan D G,Liu X D,Cai L,et al.The research of BP neural network training based on the chaos ant colony optimization[J].Microelectronics and Computer,2009,26(4):11-14

[23] 吴锋,周昊,郑立刚,等.基于变尺度混沌蚁群算法的飞灰中的碳质量分数优化[J].浙江大学学报(工学版),2010,44(6):1127-1132 Wu F,Zhou H,Zheng L G,et al.Application of scaleable chaotic ant colony algorithm in control of unburned carbon in fly ash[J].Journal of Zhejiang University:Engineering Science,2010,44(6):1127-1132

[24] 耿艳香,孙云山,谢靖鹏,等.混沌蚁群算法在图像边缘检测中的应用[J].计算机工程与应用,2015,51(2):194-197 Geng Y X,Sun Y S,Xie J P,et al.Research on chaotic ant colony algorithm in image edge detection[J].Computer Engineering and Applications,2015,51(2):194-197

[25] 崔明勇,艾欣.基于混沌蚁群算法的微网多目标低碳调度[J].电网技术,2012,32(7):1-5 Cui M Y,Ai X.Multi-objective low carbon dispatching of micro-grid using chaotic ant swarm algorithms[J].Power System Technology,2012,32(7):1-5

[26] 段海滨,王道波,于秀芬.基于云模型的小生境MAX-MIN相遇蚁群算法[J].吉林大学学报(工学版),2006,36(5):803-808 Duan H B,Wang D B,Yu X F.MAX-MIN meeting ant colony algorithm based on cloud model theory and niche ideology[J].Journal of Jilin University:Engineering and Technology Edition,2006,36(5):803-808

[27] 段海滨,丁全心,常俊杰,等.基于并行蚁群优化的多UCAV任务分配仿真平台[J].航空学报,2008,29(增刊):192-197 Duan H B,Ding Q X,Chang J J,et al.Multi-UCAVs task assignment simulation platform based on parallel ant colony optimization[J].Acta Aeronautica et Astronautica Sinica,2008,29(S):192-197

[28] 吴新杰,陶崇娥,李媛.混沌蚁群算法在回归分析中的应用[J].辽宁大学学报,2007,34(2):101-103 Wu X J,Tao C E,Li Y.Chaotic ant colony optimization ant its application in multi-linear regression analysis problem[J].Journal of Liaoning University,2007,34(2):101-103

[29] 陈烨.用于连续函数优化的蚁群算法[J].四川大学学报(工程科学版),2004,36(6):117-120 Chen Y.Ant colony system for continuous function optimization[J].Journal of Sichuan University:Engineering Science Edition,2004,36(6):117-120

(编辑：朱文杰)

Elastic impedance inversion based on chaos ant colony algorithm

Zhang Jin,An Zhenfang,Xing Lei,An Lingfang,Zhao Xi,Chen Xiaoqi

(CollegeofMarineGeoscience,OceanUniversityofChina,Qingdao266100,China)

As a pre-stack inversion,elastic impedance inversion not only characterizes amplitude variation with offset or incident angle,but also offers more lithologic parameters,such as P-wave velocity,S-wave velocity,density,Poisson’s ratio,Lame coefficient etc.However,the common elastic impedance inversion algorithms are generalized linear methods,which are strongly dependent on initial model and easily fall into local minimum.A good nonlinear algorithm,chaos ant colony algorithm,is introduced to elastic impedance inversion in this paper.The chaos ant colony algorithm is model-independent and able to reach global minimum.Model test has demonstrated the reliability and stability of the algorithm.The inversion results of a reservoir in Shengli Oilfield are consistent with the drilling data,which proves the feasibility and effectiveness of the method.

elastic impedance,nonlinear inversion,chaos ant colony algorithm

2015-04-13;改回日期：2015-07-03。

张进(1978—)，男，博士，副教授，主要从事地震反演与储层预测研究。

邢磊(1984—)，男，博士，讲师，主要从事海洋地球物理勘探方面的研究工作。

国家自然科学基金项目(41004046和41230318)资助。

P631

A

1000-1441(2015)06-0716-08

10.3969/j.issn.1000-1441.2015.06.010