基于二次电场的可控源电磁法三维矢量有限元正演模拟

汤文武,李耀国,柳建新,刘春明

(1.东华理工大学放射性地质与勘探技术国防重点学科实验室,江西南昌330013;2.中南大学地球科学与信息物理学院,湖南长沙410083;3.有色资源与地质灾害探查湖南省重点实验室,湖南长沙410083;4.Center for Gravity,Electrical & Magnetic Studies,Department of Geophysics,Colorado School of Mines,Golden CO80401,USA)

基于二次电场的可控源电磁法三维矢量有限元正演模拟

汤文武1,2,3,李耀国4,柳建新2,3,刘春明2,3

(1.东华理工大学放射性地质与勘探技术国防重点学科实验室,江西南昌330013;2.中南大学地球科学与信息物理学院,湖南长沙410083;3.有色资源与地质灾害探查湖南省重点实验室,湖南长沙410083;4.Center for Gravity,Electrical & Magnetic Studies,Department of Geophysics,Colorado School of Mines,Golden CO80401,USA)

可控源电磁法作为地震勘探的重要补充手段,可通过研究地下介质电性的变化达到监测油藏的目的。为了从理论上研究可控源电磁法在油藏监测方面的应用前景,在前人研究的基础上,对三维可控源电磁法的正演模拟算法开展了进一步的研究。为克服场源附近总场变化快、基于总场求解时难以精确模拟的问题,采用均匀半空间或水平层状介质模拟的一次场作为场源;针对传统的节点型有限元模拟电场时存在散度条件不满足的问题,采用矢量有限元对基于二次电场的偏微分方程进行离散求解；多频点正演时引入频率适应网格,可以在保持正演精度的同时提高计算速度。对比3层电导率模型的有限元数值解与解析解,验证了算法的正确性。通过一个简单的油藏模型正演模拟,从理论上证明了可控源电磁法应用于油藏监测的可能性。

二次电场;可控源电磁法;矢量有限元;正演模拟;油藏监测

电磁法是以电性差异为基础的一类勘探方法,作为地震勘探的一个重要补充手段已逐步应用于油气勘探及油藏监测等领域[1-2]。电磁法数值模拟是电磁资料解释的基础,受计算机资源及数值模拟方法的限制,目前实际生产中主要应用一、二维正反演技术。近年来,随着计算机可用内存的扩大及计算速度的不断提高,三维电磁法数值模拟研究得到了极大的发展。如Newman等[3]发表了关于三维交错网格有限差分法的航空电磁数值模拟研究成果,通过计算二次场避免了源的奇异性。Druskin等[4]应用频谱Lanczos分解法进行三维感应电磁法的模拟计算,在避免伪解出现的同时有效地加快了线性方程组数值解的收敛。Haber等[5]、Badea等[6]、Puzyrev等[7]先后研究了基于电磁耦合势的可控源三维电磁正演模拟,避免了直接基于电场求解低频电磁响应时可能出现的线性方程组数值解收敛慢的问题,但通过耦合势求取电场需引入的数值导数运算会损失部分精度。Streich[8]开展三维有限差分法可控源电磁模拟,利用MUMPS直接法求解器求解线性方程组,特别适用于多激发源的正演计算。Avdeev[9]对三维电磁数值模拟的正反演研究现状进行了较为系统的论述。国内也有许多学者开展了三维电磁数值模拟研究,如张继锋等[10]基于电场的矢量波动方程进行了可控源电磁的有限元三维模拟研究,通过引入散度条件避免了伪解的出现。徐志锋等[11]基于磁矢量势及电标量势对三维可控源电磁进行了模拟计算,通过引入罚项及稳定化算法克服了数值不稳定性。汤井田等[12]采用有限元-无限元耦合法对频率域三维可控源电磁进行了正演计算,较大程度地减少了网格计算区域,提高了正演速度。

可控源电磁法是继大地电磁测深法后发展起来的一类人工源电磁勘探方法,因克服了天然场源信号的随机性而得到了广泛的应用。快速、高精度的三维可控源电磁法正演模拟对于电磁法的灵敏度分析及反演至关重要。当前三维可控源电磁法的正演模拟可直接基于电场求解或基于耦合势求解。基于耦合势的方式由于需要进一步的数值求导(以得到电场),因而会损失部分精度。基于电场的正演方式主要利用传统的节点型有限元进行求解,一般需要施加散度校正以获得精确解。本文在前人研究工作的基础上,对三维可控源电磁法的正演算法开展了进一步的研究。首先从电磁场理论出发,采用基于二次电场的偏微分方程进行求解,应用基于棱边的矢量有限元法,采用频率适应网格进行多频点正演计算；然后设计了一个简单的储层模型,通过对电场分量的模拟计算,显示了可控源电磁法在油气勘探及油藏监测中的应用前景。

1 理论基础

1.1 偏微分方程的建立

电磁类勘探方法均基于电磁场理论,在频率域中，准静态条件下的电磁场满足以下麦克斯韦方程组[13]:

式中:E指电场矢量，H指磁场矢量，Jc为外电流密度矢量；μ0为真空中的磁导率;σ为电导率。我们假设时谐因子为e-i ωt，对公式(1) 两边求取旋度并代入公式(2)，得到以下关于电场矢量的双旋度方程：

(3)

对于电偶源、磁偶源等致密激发源,电场在源所处的位置是奇异的,并且在源的周围变化极快。若直接计算总场,需要在源的周围加密网格,这将大大增加计算量。为了消除源的奇异性,可将总场分解为一次场和二次场(异常场)。首先计算均匀半空间或水平层状介质模型的一次场,再将一次场作为场源项来求解二次场，有:

(4)

式中:Ep为一次场，Es为二次场。与推导的总场双旋度方程类似，对应于一次场的双旋度方程表示如下：

(5)

式中:σp对应计算一次场时的电导率分布,一般采用均匀半空间或水平层状介质模型。将公式(3)减去公式(5)并进行化简后得到:

(6)

式中:σa为异常电导率分布，且σa=σ-σp。因此，右端项iωμ0σaEp即为计算二次场的场源项，可通过计算异常电导率区域的一次场得到。而均匀半空间及水平层状介质模型的电场可通过快速汉克尔变换[14]计算得到。相比总场计算方式，基于二次场的模拟计算方式的另一个优势是，通过一次场的计算来加载源项，统一了源项的处理，因而适用于不同激发源下的电磁场响应的计算。

1.2 边界条件

由于采用基于二次场的偏微分方程进行正演计算,当边界距离目标研究区域足够远时,二次场可近似为0。因此,可采用边界值为0的狄利克雷边界条件:

(7)

式中:n为边界面上的法向单位矢量。值得注意的是,当一次场是通过均匀半空间模型计算得到时,该边界条件相当于基于总场方式时采用远区的均匀半空间值作为边界值的人工截断边界条件[7-8]。当采用更复杂的模型计算一次场时,该边界条件则变得更优。

2 矢量有限元分析

为了精确表征电场法向分量在不同电导率界面上的不连续性,这里采用矢量有限元[15]对基于二次电场的偏微分方程进行离散求解,采用伽辽金有限元方法推导其有限元方程。

2.1 有限元网格剖分

为了讨论方便,采用立方体剖分单元对整个模拟计算区域进行剖分。如图1所示,中间的目标研究区域采用较密的网格,由内而外采用渐变稀疏的网格进行剖分,注意网格大小递增的比例不超过1.5。采用这种非均匀渐变稀疏网格,一方面能在目标研究区域内获得精确的电磁场值,另一方面,在边界条件得到满足的情况下,网格数更少,从而可以减少正演计算量。对于包含多个频率的正演计算,通常将边界置于2～3倍最低频率下的趋肤深度之外。

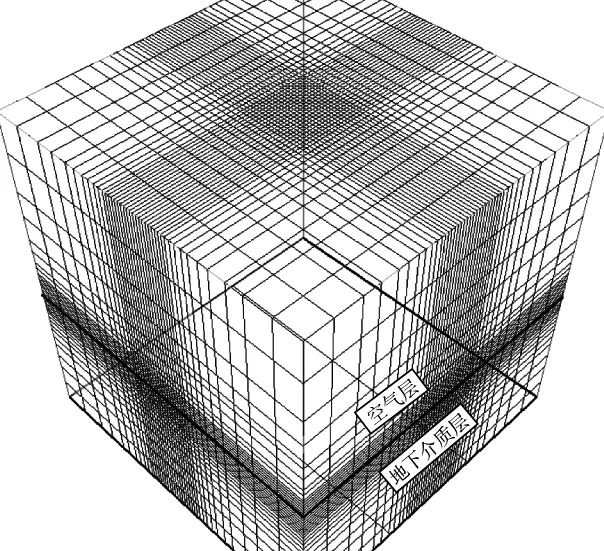
图1 网格剖分

2.2 有限元方程推导

在基于棱边的矢量有限元中,电场分量被置于各个剖分单元的棱边上的中点处,与交错网格有限差分法的做法类似。如图2所示,每个剖分单元内电场分量的采样数为12。假设对应于各分量的插值函数(形函数)为uj,则一次电场及二次电场可分别表示如下:

(8)

(9)

式中:Epj及Esj分别为各个棱边中点的一次电场及二次电场值,N为剖分区域内总的棱边数。将公式(8)及公式(9)代入公式(6)中得到:

(10)

求取每个插值函数ui与公式(10)等号两边各项的内积,并对其在整个剖分区域V上进行积分,可得到如下方程:

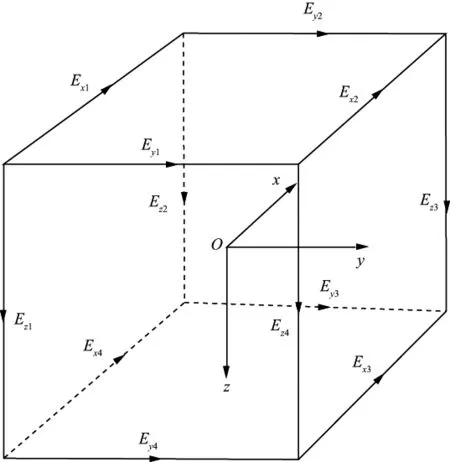
图2 电场分量在各个单元的布置

(11)

(12)

式中:S代表外边界面,n为外边界面上的外法向单位矢量。当应用边界值为0的狄利克雷边界条件时,公式(12)中的面积分项为0,公式(11)可化为:

(13)

3 线性方程组的求解

对公式(13)离散并积分后,可得到一个大型的对称复系数线性方程组。对于三维电磁法的数值模拟计算而言,该线性方程组的求解尤为重要。求解方法通常要兼顾内存需求及计算速度，本文考虑三维电磁模拟程序在个人计算机上运行的需要,采用内存需求方面更经济的迭代法。对刚度矩阵采用只存储非零元素的稀疏存储方式,同时,由于线性方程组条件数极大,采用不完全乔列斯基分解法对方程组进行预条件处理[16]。综合对比了各种常用的Krylov迭代法后,选取了最适合本文研究课题的QMR(Quasi-Minimal Residual)方法[17]对方程组进行迭代求解。

4 频率适应网格及其应用效果

进行频率域可控源电磁法正演模拟及反演成像时,通常需要同时获得多个频点的电磁场数据。而电磁法勘探的探测深度与频率有关,为了保证计算精度,设计网格时要考虑特定的频率大小，通常采用两种方法来实现:一是针对每个频率设计相对应的计算网格,这样可使得网格最小,正演计算时间最短,但是需要花费额外的时间来设计多套网格,而且不易应用到多频点数据的反演中;二是设计一个同时兼顾所有频点下电磁场数据计算精度的网格,这将使得网格最大化,正演时间会大大增加。

考虑到文中采用边界值为0的第一类边界条件,在中心网格之外需要额外的非均匀网格扩展到2～3倍最大趋肤深度(与最低频率对应)以尽量消除边界的影响。为了论述方便,我们将这些额外用来消除边界影响的网格称为附加网格,中间区域的网格称为目标网格。实际上,随着频率升高,趋肤深度减小,参与计算的附加网格数也可减少。因此,我们首先根据所有频率设计好包含目标网格及附加网格的固定网格,当从低频至高频进行正演计算时,逐步减少附加网格的数目(保持目标网格不变),从而逐步减少高频时正演的计算量,最终达到减少总的正演计算时间的目的。同时,由于目标网格及各个频点利用到的附加网格的网格间距都始终保持不变,因此可以直接将其应用到反演过程中,减少网格设计的工作量。

图3为一个3层水平电阻率模型。第1层的电阻率为100Ω·m,厚度为1075m;第2层的电阻率为10Ω·m,厚度为250m;第3层的电阻率为100Ω·m。单位电偶源置于坐标原点O处,分别采用非频率适应网格(一套同时兼顾各个频率的固定网格)及频率适应网格对频率范围为1～128Hz的8个频点进行正演计算。

图4为两种不同网格的正演计算精度对比,所计算的频率为16Hz。其中图4a为二次电场x分量,图4b为二次电场y分量。由图4可见,两种不同网格正演计算得到的二次水平电场分量基本一致,频率适应网格与非频率适应网格的相对误差小于1%,说明了频率适应网格的可行性。表1为不同频率下两种网格的正演计算时间对比情况。由表1 可知,在多频点正演计算时,采用频率适应网格可以使得高频点的正演速度逐步提高,单频点的最大加速比约为2,从而可减少总体正演计算的时间。这是因为随着频率的逐步提高,实际被用于计算的网格逐步减少。由此可知,频率适应网格在多频点正演计算时,既能加快正演计算的速度,又能保持正演计算的精度。

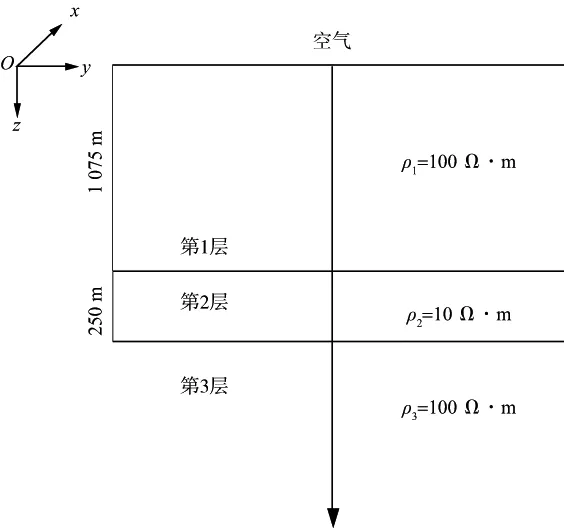
图3 3层电阻率模型

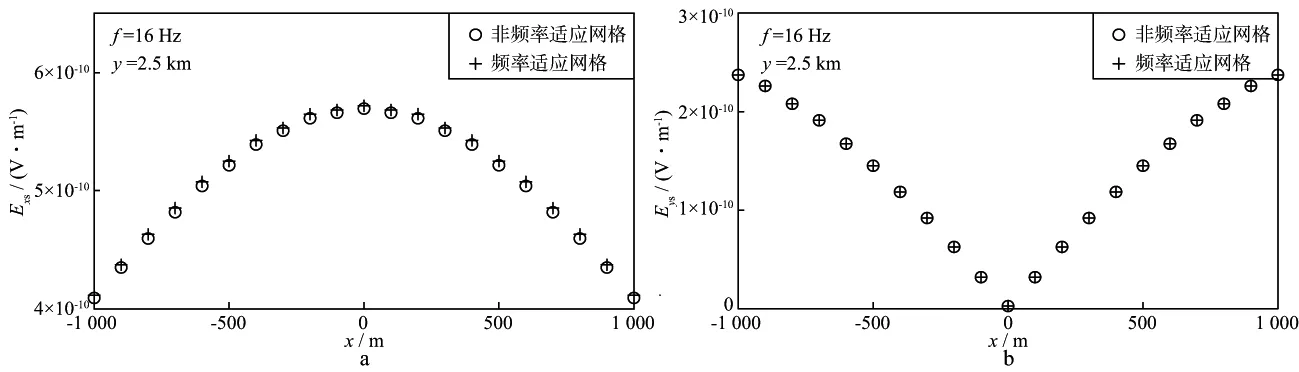
图4 非频率适应及频率适应网格正演计算精度对比

表1 非频率适应及频率适应网格正演计算时间对比

频率/Hz1248163264128非频率适应网格/s180155148137125110106102频率适应网格/s1811511239984675952加速比1．001．031．201．381．491．641．801．96

5 算法精度验证及模型算例

5.1 算法精度验证

为了验证本文算法的正确性及精度,我们以图3 中的3层水平电导率模型为例进行有限元正演计算。由于水平层状介质模型有解析积分形式,通过快速汉克尔变换[14]可以计算出相应的解析解,对比验证本文算法的正确性及精度。

将沿x方向的单位电偶源置于坐标原点,在y=2.5km，长为2km的关于y轴对称的测线上观测二次电场的水平分量,测点间距为100m。基于电导率为100Ω·m的均匀半空间模型计算得到一次场,将该一次场作为场源计算对应的二次场。采用的剖分网格大小为71×61×50,即x,y及z方向分别剖分为71,61及50个单元,其中z方向包括20个空气层及30个地下介质层。中间的目标研究区域在水平方向上采用较小的网格进行均匀剖分,外围层逐渐扩大到约3倍最低频率时的趋肤深度。在垂直方向上靠近地面处采用较小的网格剖分,同时在异常电导率区域剖分较细,远离界面时采用逐渐增大的网格扩展到约3倍趋肤深度处。

图5a是二次电场x分量的有限元数值解及解析解对比,计算的频率为1Hz,图5b为数值解与解析解之间的相对误差。分析图5a可知,数值解的实部及虚部分别与解析解的实部及虚部吻合。由图5b可以看出,数值解实部的相对误差均在1%以下,而虚部的相对误差在2%～3%,满足精度要求。观察图5a发现，实部数值远大于虚部,这可能是导致虚部误差较实部误差大的原因之一。实部及虚部的误差分布呈锯齿状则与剖分网格情况有关,因为在水平方向上的最小网格间距为200m,而测点间距为100m,分布在两个单元之间的测点的误差相对偏大。

图6为二次电场y分量的有限元数值解及解析解的对比及其相对误差。同样可见有限元数值解的实部及虚部分别与解析解的实部及虚部吻合(图6a),实部及虚部的误差均在1%以下(图6b),满足精度要求。

5.2 模型算例

图7为一个简化的储层模型示意图,用以研究油气开采过程中从油气底部注入盐水时地面上的电磁响应变化规律。模型为3层电导率介质,有一个代表油气的高阻梯形区域埋藏其中。第1层的电阻率为100Ω·m,厚度为0.5km;第2层的电阻率为10Ω·m,厚度为2km;底层(基岩)的电阻率为200Ω·m。发射源为处于原点并沿x方向的单位电偶极。水平x方向长为6km,y方向顶部宽为3km,底部宽为4km的梯形油藏关于y轴对称,其中心距离发射源的水平距离为2.8km。油藏顶部距离地面1.5km,油气及注入盐水在深度方向的总厚度为0.5km。其中,油气的电阻率设为500Ω·m,盐水的电阻率设为1Ω·m。当发射源发射时谐电磁信号时,在地面上观测电场信号。

图5 二次电场x分量精度验证

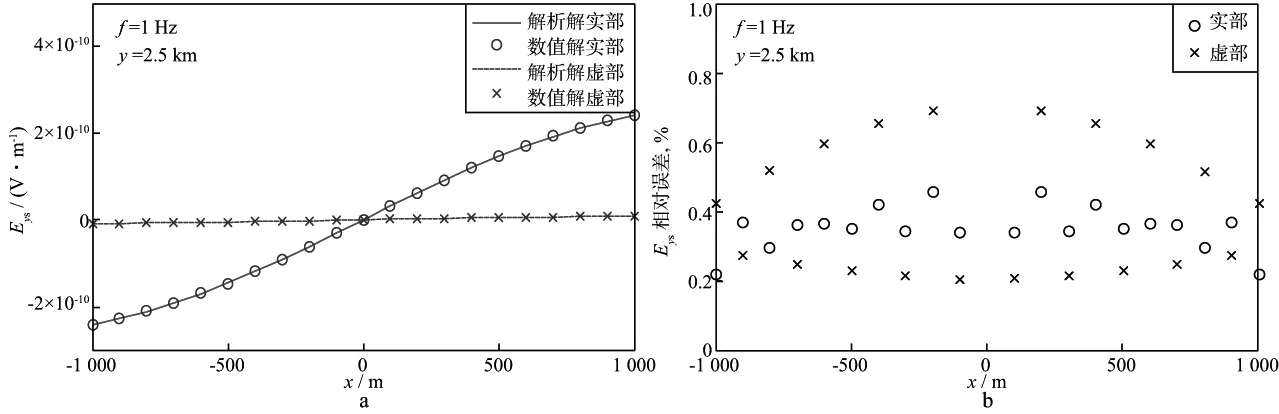
图6 二次电场y分量精度验证

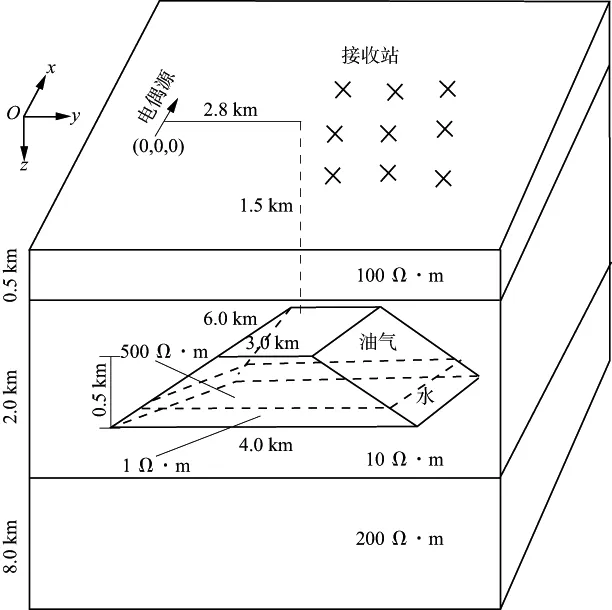
图7 简单储层模型

为了研究模型中油藏的电磁响应情况,我们设计如下模拟计算方案:当油气层的厚度分别为400,300及200m,水层厚度分别为100,200及300m时,计算相应3个时刻下的二次电场(异常场),并计算二次场与总场的百分比,采用的频率为1Hz。这里只展示二次电场是因为一次场在激发源附近占主导地位,在总场的分布变化图中很难区分不同时刻的异常场变化。图8为电场x分量异常场的实部变化情况,其中图8a,图8b,图8c分别对应油气厚度400,300及200m时刻的二次场;图8d,图8e,图8f 分别为这3个不同时刻二次场占总场的百分比。观测图8可知,异常场的幅度最大达10-11V·m-1,若实际仪器的可探测精度为10-9V·m-1,则将激发源的电偶极距增大为100A·m时,异常场便处于可探测的范围。从图8a 至图8c,异常场的分布也发生了变化,总体上场值呈增大的趋势,这是由于水层厚度逐渐变大并逐渐靠近激发源。观察每一时刻的二次场分布图,发现油气区域边界附近的异常值较大,为勘探油气的有利观测区域。同时,在实际勘探中,电磁场数据不可避免会夹杂噪声,若假设噪声水平为5%,则当异常场与总场的比值大于5%时即可发现异常的存在。观察图8d至图8f 可知,在油气区域边界附近,相对异常较大(部分区域远大于5%),有利于目标储层的勘探,并且随着水层厚度增大,有利探测区域也增大。图9为油气厚度变化时的异常差值(时移异常),其中图9a 为油藏厚度从400m减少到300m时的异常差值,图9b为油藏厚度从300m减少到200m时的异常差值。由图9 可知,当从油气底部注入水时,油气在地面上的投影位置区域可以观测到较大的时移异常,从而为油藏的监测提供指示。

图8 电场x分量异常场实部变化

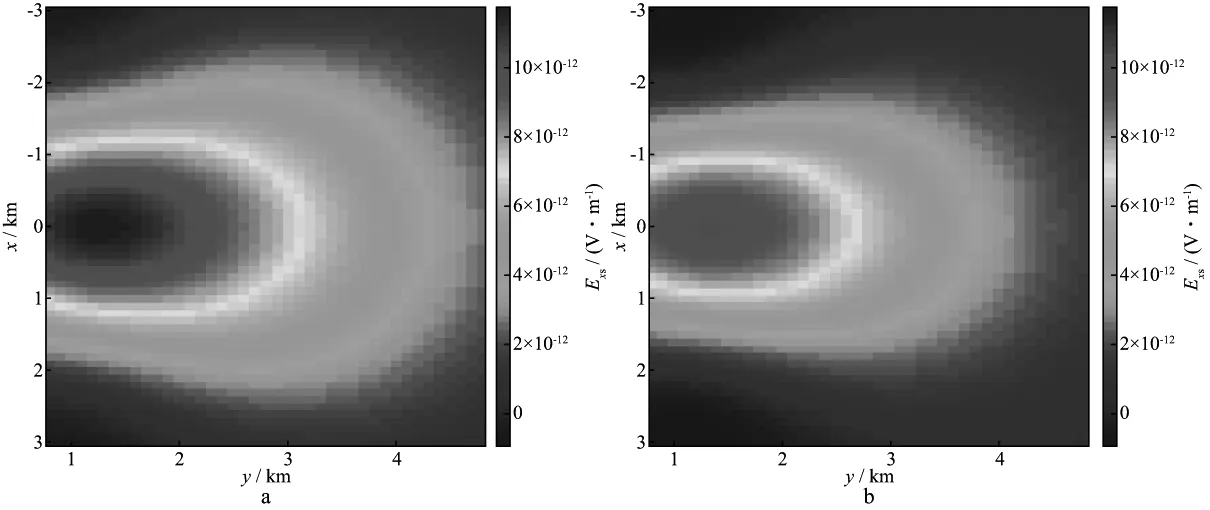
图9 电场x分量实部时移异常

类似地,图10为相同条件下电场x分量异常场虚部变化图。观察可知,异常场虚部的最大幅度达10-11V·m-1,因此当激发源增大到100A·m时,虚部分量也处于可探测范围内,且在油气区域边界处有较大异常值。比较分析虚部异常场与总场的比值可知,在油气区域的边界及以外区域,相对异常较大,处于可探测范围；同时,当水位上升时,可探测范围增大。图11为油气厚度变化时的时移异常,与实部情况类似,虚部的时移异常也可为油藏的变化提供指示信息。

图10 电场x分量异常场虚部变化

图11 电场x分量虚部时移异常

6 结束语

本文利用矢量有限元方法实现了三维可控源电磁法的正演模拟。该方法能够精确模拟电场法向分量在不同电导率界面的不连续性,且在剖分单元内自动满足散度条件，采用的频率适应网格能够在保持计算精度的同时,加快多频点正演计算速度。模拟计算结果表明,可控源电磁法能有效探测到高阻油藏,显示了可控源电磁法在油藏监测方面的应用前景。

下一步研究工作是将该方法与传统的节点型有限元可控源电磁法进行对比，同时开展三维反演研究,进一步检验频率适应网格在反演中的应用效果。

[1] 沈金松,孙文博.二维海底地层可控源海洋电磁响应的数值模拟[J].石油物探,2009,48(2):187-194 Shen J S,Sun W B.The numerical simulation of controlled source marine electromagnetic response for 2-D seabed stratum[J].Geophysical Prospecting for Petroleum,2009,48(2):187-194

[2] 唐新功,胡文宝,严良俊,等.瞬变电磁法油藏动态监测模拟[J].石油物探,2004,43(2):192-195 Tang X G,Hu W B,Yan L J,et al.The application of transient electromagnetic in reservoir monitoring[J].Geophysical Prospecting for Petroleum,2004,43(2):192-195

[3] Newman G A,Alumbaugh D L.Frequency-domain modeling of airborne electromagnetic responses using staggered finite differences[J].Geophysical Prospecting,1995,43(8):1021-1042

[4] Druskin V L,Knizhnerman L A,Lee P.New spectral Lanczos decomposition method for induction modeling in arbitrary 3-D geometry[J].Geophysics,1999,64(3):701-706

[5] Haber E,Ascher U M,Aruliah D A,et al.Fast simulation of 3D electromagnetic problems using potentials[J].Journal of Computational Physics,2000,163(1):150-171

[6] Badea E A,Everett M E,Newman G A,et al.Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials[J].Geophysics,2001,66(3):786-799

[7] Puzyrev V,Koldan J,de la Puente J,et al.A parallel finite-element method for three-dimensional controlled source electromagnetic forward modelling[J].Geophysical Journal International,2013,193(2):678-693

[8] Streich R.3D finite-difference frequency-domain modeling of controlled-source electromagnetic data:direct solution and optimization for high accuracy[J].Geophysics,2009,74(5):F95-F105

[9] Avdeev D B.Three-dimensional electromagnetic modelling and inversion from theory to application[J].Surveys in Geophysics,2005,26(6):767-799

[10] 张继锋,汤井田,喻言,等.基于电场矢量波动方程的三维可控源电磁法有限元法数值模拟[J].地球物理学报,2009,52(12):3132-3141 Zhang J F,Tang J T,Yu Y,et al.Three-dimensional controlled source electromagnetic numerical simulation based on electromagnetic vector wave equation using finite element method[J].Chinese Journal of Geophysics(In Chinese),2009,52(12):3132-3141

[11] 徐志锋,吴小平.可控源电磁三维频率域有限元模拟[J].地球物理学报,2010,53(8):1931-1939 Xu Z F,Wu X P.Controlled source electromagnetic 3-D in frequency-domain by finite element method[J].Chinese Journal of Geophysics(In Chinese),2010,53(8):1931-1939

[12] 汤井田,张林成,公劲喆,等.三维频率域可控源电磁法有限元-无限元结合数值模拟[J].中南大学学报(自然科学版),2014,45(4):1251-1260 Tang J T,Zhang L C,Gong J Z,et al.3D frequency domain controlled source electromagnetic numerical modeling with coupled finite-infinite element method[J].Journal of Central South University(Science and Technology),2014,45(4):1251-1260

[13] Nabighian M N.Electromagnetic methods in applied geophysics:theory[M].Tulsa:Society of Exploration Geophysics,1987:131-138

[14] Guptasarma D,Singh B.New digital linear filters for Hankel J0 and J1 transforms[J].Geophysical Prospecting,1997,45(5):745-762

[15] 金建铭.电磁场有限元方法[M].王建国,译.第1版.西安:西安电子科技大学出版社,2001:292-300 Jin J M.Electromagnetic FEM[M].Wang Jianguo,translator.1st ed.Xi’an:Xidian University Press,2001:292-300

[16] Smith J T.Conservative modeling of 3-D electromagnetic fields,part II:biconjugate gradient solution and an accelerator[J].Geophysics,1996,61(5):1319-1324

[17] Freund R W,Nachtigal N M.An implementation of the QMR method based on coupled two-term recurrences[J].SIAM Journal on Scientific Computing,1994,15(2):313-337

(编辑：戴春秋)

Three-dimensional controlled-source electromagnetic forward modeling by edge-based finite element using secondary electric field

Tang Wenwu1,2,3,Li Yaoguo4,Liu Jianxin2,3,Liu Chunming2,3

(1.FundamentalScienceonRadioactiveGeologyandExplorationTechnologyLaboratory,EastChinaInstituteofTechnology,Nanchang330013,China; 2.SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha410083,China; 3.KeyLaboratoryofNonferrousResourcesandGeologicalHazardExploration,Changsha410083,China; 4.CenterforGravity,Electrical&MagneticStudies,DepartmentofGeophysics,ColoradoSchoolofMines,GoldenCO80401,USA)

As an important complementary tool for seismic survey,the controlled-source electromagnetic (EM) method can be used to monitor reservoirs by detecting the subsurface electrical properties.In order to investigate theoretically feasibility of monitoring reservoirs by the controlled-source EM,a requisite component is to calculate the EM responses of three-dimensional conductivity model excited by the EM sources.Total fields varies rapidly and is difficult to simulate accurately for the region adjacent to the source locations,to this end,the primary field is calculated for a half-space or a layered-earth model as the source term.To bypass the problem that the divergence condition is unsatisfied when using traditional nodal element to model the electrical field,the partial deferential equation (PDE) for the controlled-source EM,based on the secondary electric field,is solved discretely by the edge-based finite element method.To model the responses at multiple frequencies,the frequency-adaptive mesh can be used to increase the speed of forward calculation while maintaining the accuracy.The algorithm is verified by comparing the analytic solution with the numerical solution for a three-layered conductivity model.The modeling results of a simple reservoir model demonstrate the possibility of the controlled-source electromagnetic method in reservoir monitoring.

three-dimensional,controlled-source electromagnetic method,edge-based finite element,forward modeling,reservoir monitoring

2015-04-07;改回日期：2015-08-19。

汤文武(1987—),男,博士,讲师,主要研究方向为电磁法数值模拟及反演成像。

刘春明(1974—),男,博士,讲师,主要研究方向为电磁法勘探及数值模拟。

国家自然科学基金项目(41174103)、国家高技术研究发展计划(863计划)项目(2014AA06A615)、湖南省自然科学基金项目(2015JJ2151)联合资助。

P631

A

1000-1441(2015)06-0665-09

10.3969/j.issn.1000-1441.2015.06.004