PML边界条件下孔隙介质弹性波可变网格正演模拟方法研究

孙林洁,刘春成,张世鑫

(中海油研究总院,北京100028)

PML边界条件下孔隙介质弹性波可变网格正演模拟方法研究

孙林洁,刘春成,张世鑫

(中海油研究总院,北京100028)

孔隙介质弹性波正演模拟对于储层预测和油气检测具有重要的指导意义。为提高孔隙介质波场正演模拟的精度,将可变网格方法应用于基于Biot理论的双相介质弹性波高阶有限差分正演模拟方法中,有效解决了二阶混合偏导数差分近似的可变网格过渡问题,推导了基于PML边界条件的可变网格差分格式,实现了空间与时间步长任意整数倍变化的双相介质弹性波可变网格正演模拟。对于细微地质结构或横向变化剧烈的介质区域,利用可变网格对区域精细重采样可有效提高正演的模拟精度;对于介质相对稳定的区域,采用大步长采样可保证正演计算效率。数值试验结果表明,与常规正演模拟方法相比,双相介质可变网格正演模拟方法的精度、效率有明显提高,对精细研究孔隙介质地震响应有着重要意义。

Biot理论;孔隙介质;PML边界条件;可变网格;有限差分

近年来,随着石油勘探开发技术的发展,对孔隙介质的关注程度日益提高。当孔隙中含有流体时,不同流体的存在会对介质参数产生不同的影响,从而影响到地震反射波的走时、振幅和频率等特征[1]。因此,根据油气储层在不同地层条件和流体相态下的地震波反射特征进行正演模拟,分析不同孔隙流体的地球物理特性在各种地震信息上的表现,总结规律和认识,对指导储层预测和油气检测等工作具有重要意义。

波动方程正演模拟方法是探索地震波在介质中传播规律的重要手段。常规波动方程正演模拟方法基于等效理论,不单独考虑介质孔隙中的流体,将介质中固、液两相对地震波的作用简化为等效介质参数,所得到的模拟结果无法体现流体响应特征。Biot提出的双相介质理论[2-3]已经得到广泛应用,Biot模型假设岩石由骨架和孔隙中的流体构成,这种模型假设考虑了孔隙流体的作用[4-5],比等效单相介质模型更为符合实际情况[6],适合讨论、分析含流体储层的地震响应特征。

有限差分方法是一种常用的波动方程数值解法,具有精度高、计算速度快的优点,但是该方法也具有一定局限性,如存在数值频散,且必须满足方法稳定性条件等[7]。常规差分方法使用规则网格对模型进行剖分,一般在同一模型内部使用统一的采样步长。而孔隙介质多为非均匀介质,模型参数在不同区域变化并不均匀,使用单一尺度的网格步长对模型进行剖分,必然会导致局部过采样影响计算效率或局部采样不足影响模拟精度。Moczo[8]首次提出可变网格的思路,数值模拟时根据模型参数变化调整计算网格步长,针对尺度较小的地质体和模型参数横向变化剧烈的区域采用精细网格剖分;针对模型参数变化平缓的区域采用大网格剖分。这种方法既可以保证正演模拟的精度,同时在一定程度上提高了计算效率。

可变网格方法提出至今已被成功应用于常规单相介质声波[9-11]、弹性波[12-14]的有限差分正演模拟当中。本文将可变网格方法推广至基于Biot理论的双相介质弹性波二阶位移方程的正演模拟中,成功地解决了二阶混合偏导数常规差分近似的可变网格过渡问题。文中正演模拟使用孔隙介质的完全匹配层(PML)边界条件,推导了可变网格区域靠近模型边界时的差分格式,从而得到任意倍数、任意可变网格位置的孔隙介质可变网格正演模拟算法,实现了对孔隙介质的高效、精确数值模拟。

1 方法原理

1.1 双相介质弹性波方程PML差分格式

Biot给出的弹性波方程形式为[2]:

(1)

式中:u和U分别为固相与液相位移;e和ξ分别为固相与液相介质的体应变;A,N,Q,R为双相介质弹性参数,表征固相、液相介质的弹性性质与相互的耦合作用;ρ11,ρ22,ρ12为双相介质质量参数,表征固相、液相介质单位体积的等效质量与相互作用对质量的影响;B为耗散参数,表征液相粘滞性对地震波的衰减效果。将方程(1)展开成为二阶位移形式,在二维情况下,以x方向为例,有:

(2)

一般而言,求解弹性波方程PML差分格式需要将原方程加入衰减项后根据空间导数方向拆分,并通过坐标变换的方式得到与原方程同解的稳定边界格式[15]。与弹性波方程中仅包含二阶时间导数的情况不同,考虑介质耗散的双相弹性波方程中同时存在一阶与二阶时间导数,分解方程会形成欠定方程组。为简化这个问题,从PML边界条件吸收衰减方式入手,在保持原波动方程形式的同时加入衰减项。加入PML衰减项的波动方程形式需要进行以下变换[15-17]:

(3)

式中:βi为i方向的衰减项。则加入衰减项的PML方程为:

(4)

该方程解的离散差分形式求解方式详见附录A。

至此我们得到了双相介质弹性波方程的PML差分格式。在正演模拟过程中,通过多次数值试验,合理选取模型边界和角点位置的PML吸收参数,而令模型区域的吸收参数为0[15],即可消除模型边界反射,得到精确的模拟结果。

1.2 双相介质可变网格PML差分格式

可变网格有限差分方法的主要特点为:在需要精细模拟的区域使用小网格对模型进行重采样计算,其它区域使用大网格计算[11]。可变网格模型剖分的示意图如图1所示。

常规差分格式具有对称性,针对求导点选取距离对称的点参与导数计算。而可变网格算法使用不同步长剖分模型,导致采用常规差分方法计算可变网格边界区域的导数时会产生比较大的误差。同时空间步长影响算法的数值频散程度,也使得不同步长网格交界处由于算法问题而产生弱反射[18]。

如图2所示处理方式,以x方向过渡区第n个点为例,当大小网格步长比为α时,空间M阶可变网格过渡差分格式为[18]:

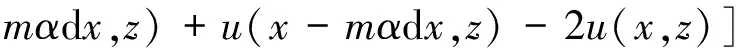
(5)

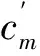
同理可以得到z方向的过渡差分格式。

为实现二维可变网格计算,则需要解决x,z方向的混合偏导数过渡问题。M阶精度差分格式计算混合偏导需要使用其周围M2个点的函数值,对于高阶差分而言,维持这个系统的对称性求解过渡差分格式显然非常复杂。考虑到求解二阶混合偏导问题可以转化为求解两个嵌套的一阶导数问题。具体推导过程参见附录B。

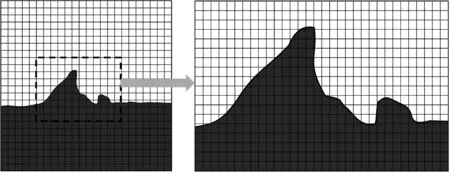
图1 可变网格剖分示意图解

图2 可变空间步长网格交界区域处理方式示意图解(星形标记代表导数计算点)

仅在某一方向上改变网格步长,上述过渡处理方式不涉及插值计算。而在两个空间维度改变网格步长时,由于计算过渡区导数值所需要的部分波场值不存在,需要插值得到。图3以二维可变网格算法为例,标出了二维可变网格计算时需要进行插值的点(图3中黑色圆点为需要进行插值的点)。

时间域显示差分格式需要空间步长与时间采样率满足一定关系来保证差分算法的稳定性,因此在调整空间网格步长时,时间采样间隔必须满足小网格的稳定性条件。若模拟计算采用统一的时间采样间隔,必然会造成大网格区的时间过采样。因此需要在时间域改变采样步长,小网格区加密时间片循环,再对计算结果采用大时间步长重采样,从而保证计算效率[18-19]。

图3 可变网格计算中需要进行插值的点

由于加密时间片循环会造成部分参与计算的时间片缺失,因此在改变时间步长时需要设置过渡带,求出大时间步长循环下当前时刻和下一时刻的波场值,插值得到小时间步长计算所需的各时刻波场值,如图4所示。由于时间差分算子精度远小于空间差分算子精度,因此时间维度上的插值计算引入的误差不会造成明显的干扰现象。

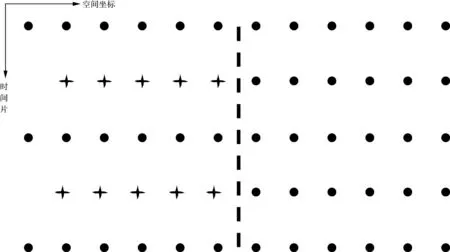
图4 可变时间步长过渡区处理方式示意图解(“十”字形记号表示需要插值得到的点)

2 模型试算

2.1 均匀介质模型

首先建立均匀介质模型,测试PML边界的吸收效果与可变网格方法的适用性。

均匀双相介质模型的弹性参数与质量参数如表1所示。模型大小为1km×1km;大网格空间步长为10m,时间步长为1.0ms;小网格空间步长为1m,时间步长为0.1ms。震源为等能量源,位于模型中心,使用主频为35Hz的Ricker子波作为震源子波。将小网格区置于模型边缘测试PML边界的吸收效果与可变网格过渡区的处理效果。

图5和图6分别给出了该均匀双相介质模型180ms的波场快照和炮记录。由图5和图6可以看到,双相介质中存在快纵波与慢纵波。固相介质中的慢纵波能量远小于同条件下快纵波的能量,而液相介质中的慢纵波能量与快纵波能量基本处于一个量级,但由于介质的耗散作用,慢纵波能量衰减迅速,因此实际情况下很难观测到慢纵波的存在。正演模拟中应用的PML边界条件可以很好地吸收传播到边界的快纵波与慢纵波,几乎不会产生任何边界反射,而将可变网格区域放置于模型角点处,使得部分小网格点参与计算PML边界的波场,计算结果中,波场快照和炮记录中都没有明显的波场异常现象,说明该过渡方法不会引入明显人为干扰,该模型验证了可变网格方法的可行性。

表1 均匀介质模型双相介质参数

图5 均匀双相介质模型180ms波场快照(黑色虚线框代表变网格区域)

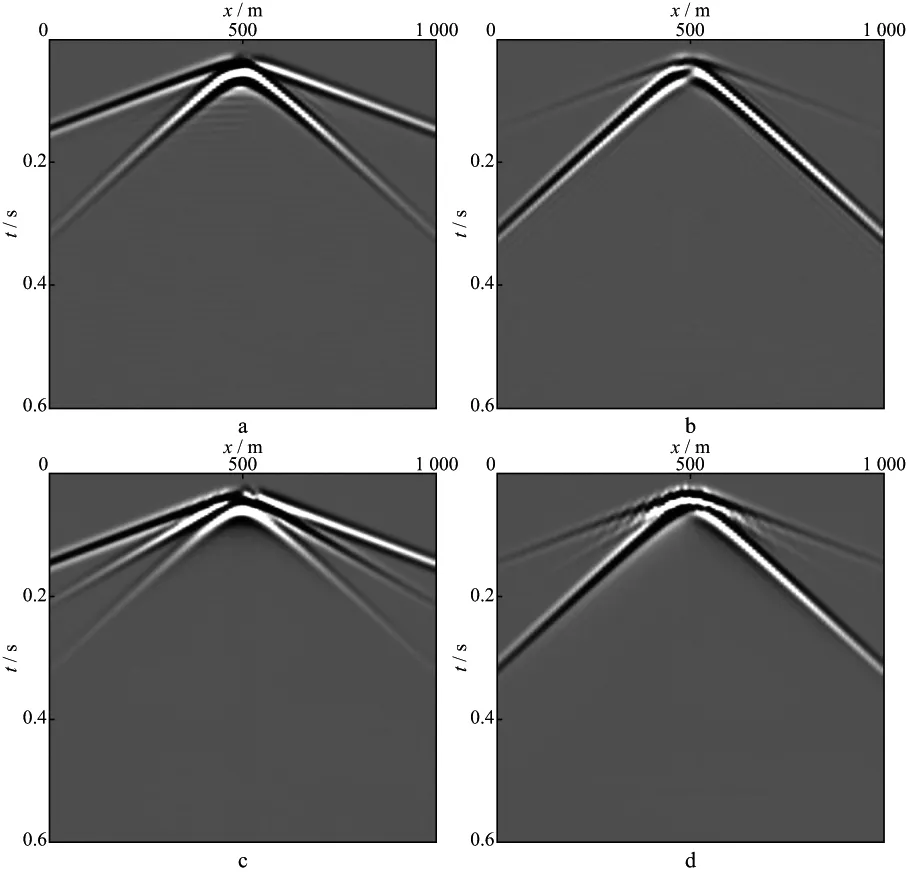
图6 均匀双相介质模型炮记录

2.2 溶洞模型

使用一个溶洞模型来测试双相介质可变网格方法在精度与计算效率方面的优势。

溶洞模型如图7所示,模型中涉及到的介质参数如表2所示。均匀单相介质背景下分布着两个溶洞,其中较大溶洞半径为50m,较小溶洞半径为4m。溶洞内部介质为双相介质。模型大小为1km×1km;大网格空间步长为10m,时间采样率为1.0ms;小网格空间步长为1m,时间采样率为0.1ms。可变网格区域如图7中虚线框所示,图中星形记号表示炮点位置。震源设置为组合纵波源,采用主频为50Hz的Ricker子波作为震源子波。对比同一模型的大网格采样模拟结果(图8a)和小网格采样模拟结果(图8b)可以看到,小网格采样不仅不会因为步长间距过大而错过较小溶洞的样点,同时更小的采样间隔也精细地刻画了较大溶洞的边缘轮廓特征,使得模拟结果更精确。

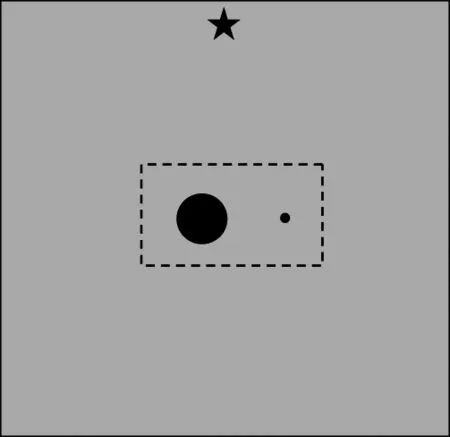
图7 溶洞模型示意图解

表2 溶洞模型双相介质参数

模型参数A/GPaN/GPaQ/GPaR/GPaρ11/(kg·m-3)ρ22/(kg·m-3)ρ12/(kg·m-3)B/(kg·m-3·s-1)溶洞内介质33．7821．113．1242．41301572．3512．5-307．50．15×105背景介质194．80162．40002078．4000

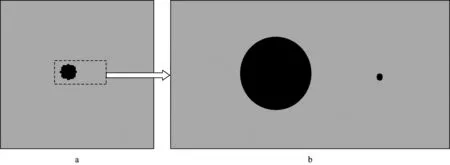
图8 溶洞模型采样模拟结果

在其它模拟参数相同的条件下,针对同一模型,计算空间步长为10m,时间步长为1.0ms的常规大网格与空间步长为1m,时间步长为0.1ms的常规小网格模拟结果,并与可变网格方法模拟结果进行比较与分析。

图9,图10和图11分别为采用大网格采样、可变网格采样与小网格采样正演模拟得到的波场快照与炮记录。由于激发与接收都在单相介质中进行,因此这里只给出固相介质中波场快照与单相介质炮记录结果。大网格采样模拟由于采样不足,较大溶洞边缘呈阶梯状,造成模拟结果中存在很多角点的绕射波。同时溶洞内部介质波速较低,流体造成能量耗散,导致溶洞内部数值频散严重。由于大网格步长大于较小溶洞半径,没有采集到较小溶洞的样点,因此模拟结果中也没有体现较小溶洞的地震响应。

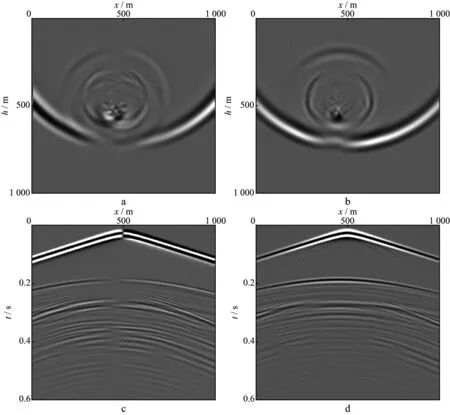
图9 溶洞模型大网格采样模拟结果

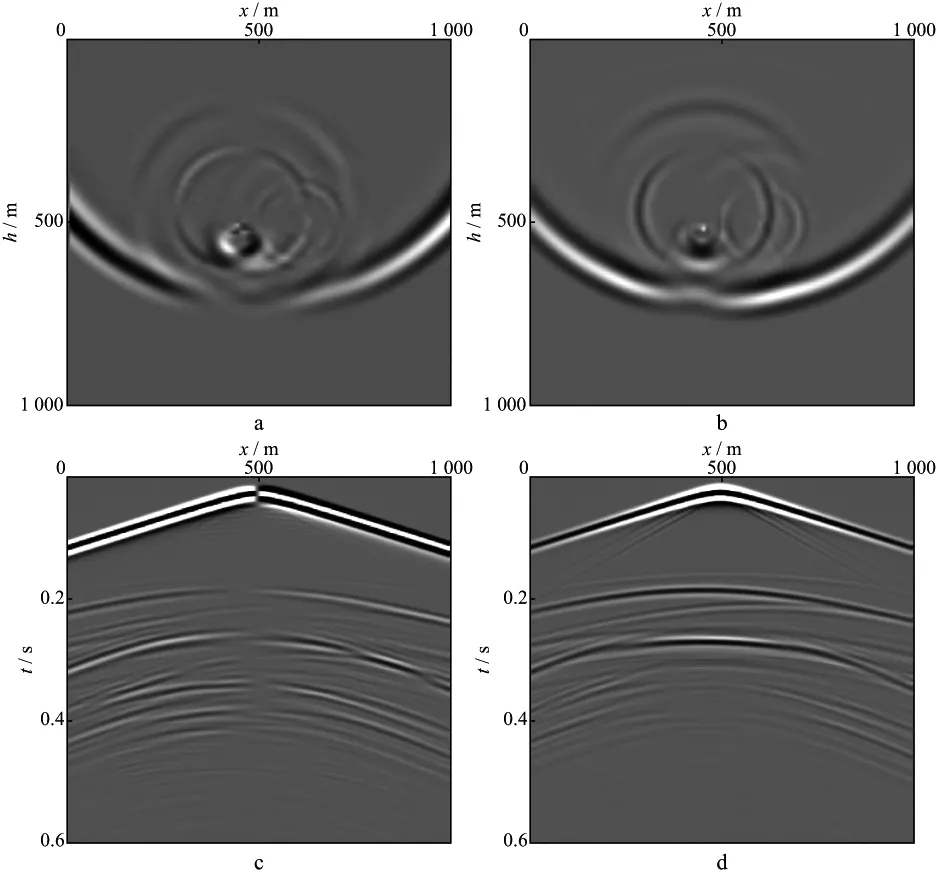
图10 溶洞模型可变网格采样模拟结果

可变网格采样模拟方法对溶洞分布区域使用小步长模拟,由于针对溶洞的采样步长较为精细,溶洞边缘较为平滑,有效降低了角点绕射波的能量,同时小步长计算也有效压制了大溶洞内部低速介质的数值频散。由于减小了采样步长,较小溶洞的响应也在模拟结果中体现出来。可变网格方法计算的结果几乎与整个模型均使用小网格模拟的结果(图11)完全一致,从而验证了可变网格方法模拟的精确性。

表3给出了对溶洞模型采用3种不同模拟方法消耗的机时与占用的内存情况。正演模拟使用的机型为HP Compaq dx2318MT,CPU为Intel CPU E8400,主频为3.0GHz,内存为4G,在Window XP系统下运行。由统计结果可以看到,整个模型使用小网格采样计算,计算机时是大网格采样计算的570倍,内存消耗是大网格采样模拟的88倍,而可变网格模拟的计算机时约为大网格采样计算机时的5倍,内存消耗约为大网格采样模拟的2倍,相对于小网格采样模拟大大提高了计算效率。

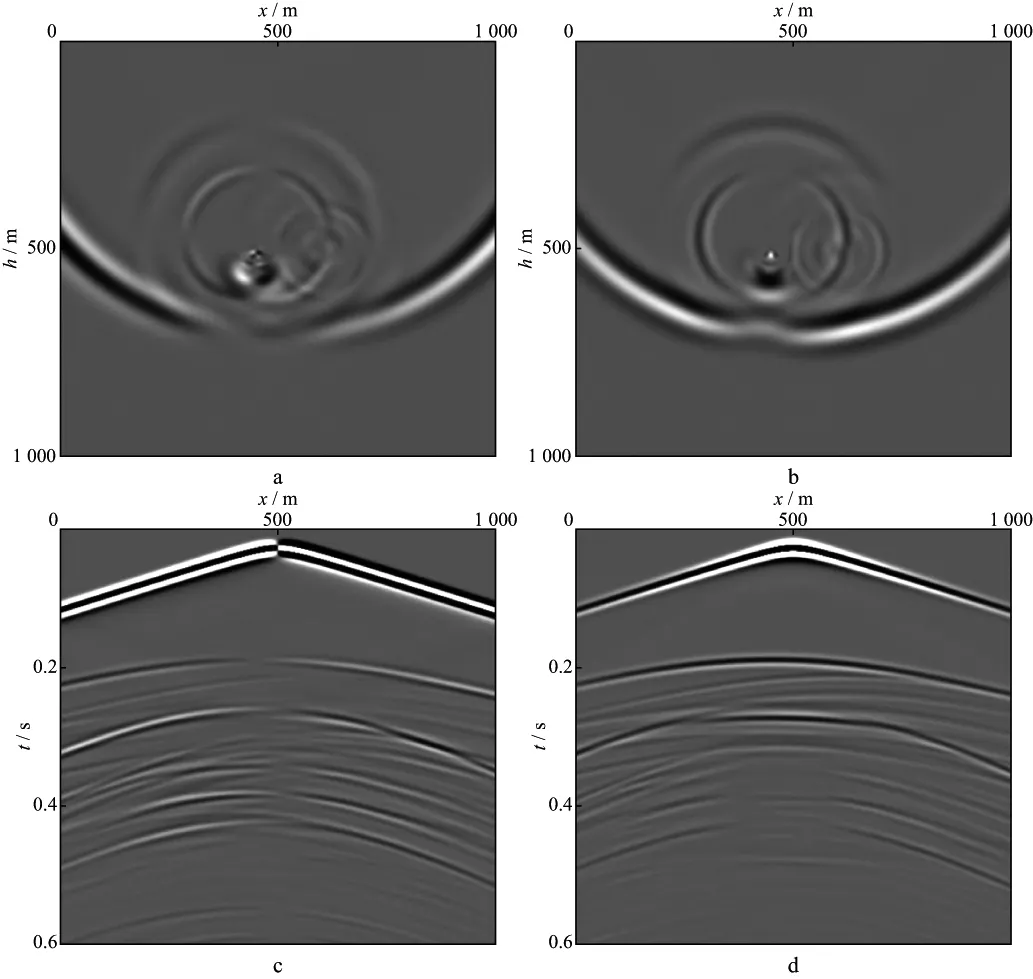
图11 溶洞模型小网格采样模拟结果

表3 溶洞模型3种模拟方法计算成本统计

模拟方法计算机时/s占用内存/KB空间步长为10m，时间步长为1．0ms的大网格常规有限差分方法3811732空间步长为1m，时间步长为0．1ms的小网格常规有限差分方法216431035240可变网格有限差分方法20225868

3 结束语

本文将可变网格方法应用于基于Biot理论的双相介质弹性波正演模拟,解决了空间二阶混合偏导数的可变网格过渡问题,并得到了可变网格过渡区PML差分格式,从而实现了任意倍数、任意位置变步长的可变网格有限差分正演模拟方法。该方法可以针对模型中重点区域进行精细刻画,有效降低矩形网格采样率低引起的人为散射问题,压制由于大网格离散引起的数值误差。文中多个模型验证了基于PML边界条件的孔隙介质弹性波可变网格正演模拟方法是一种精确、高效的双相介质弹性波正演模拟方法。将该方法应用于复杂精细双相介质模型中,能够大大提高正演模拟效率,对研究储层流体正演响应具有积极的作用。同时该方法能够推广至其它复杂波动理论,值得进一步深入研究。

[1] 杨顶辉,张中杰,滕吉文,等.双相各向异性研究、问题与应用前景[J].地球物理学进展,2000,15(2):7-21 Yang D H,Zhang Z J,Teng J W.The study of two-phase anisotropy questions and applied prospects[J].Progress in Geophysics,2000,15(2):7-21

[2] Biot M A.Theory of propagation of elasticwaves in a fluid-saturated porous solid,I:low-frequency range[J].The Journal of the Acoustical Society of America,1956,28(2):16-178

[3] Biot M A.Theory of propagation of elastic waves in a fluid-saturated porous solid,II:higher-frequency range[J].The Journal of the Acoustical Society of America,1956,28(2):179-191

[4] Biot M A.Mechanics of deformations and acoustic propagation in porous media[J].Journal of Applied Physics,1962,33(4):1482-1498

[5] Biot M A.Generalized theory of acoustic propagation in porous dissipative media[J].The Journal of the Acoustical Society of America,1962,34(9):1254-1264

[6] 赵海波,王秀明,王东,等.完全匹配层吸收边界在孔隙介质弹性波模拟中的应用[J].地球物理学报,2007,50(2):581-591 Zhao H B,Wang X M,Wang D,et al.Applications of the boundary absorption using a perfectly matched layer for elastic wave simulation inporoelastic media[J].Chinese Journal of Geophysics,2007,50(2):581-591

[7] Alford R M,Kelly K R,Boore D M.Accuracy of finite difference modeling of the acoustic wave equation[J].Geophysics,1974,39(6):834-842

[8] Moczo P.Finite-difference technique for SH waves in 2D media,using irregular girds:application to the seismic response problem[J].Geophysical Journal International,1989,99(2):321-329

[9] 黄超,董良国.可变网格与局部时间步长的高阶差分地震波数值模拟[J].地球物理学报,2009,52(1):176-186 Huang C,Dong L G.High-order finite-difference method in seismic wave simulation with variable grids and local time-steps[J].Chinese Journal of Geophysics,2009,52(1):176-186

[10] 孙林洁,印兴耀.基于PML边界条件的高倍可变网格有限差分数值模拟方法[J].地球物理学报,2011,54(6):1614-1623 Sun L J,Yin X Y.A finite difference scheme based on PML boundary condition with high power grid step variation[J].Chinese Journal of Geophysics,2011,54(6):1614-1623

[11] 孙成禹,李胜军,倪长宽,等.波动方程变网格步长有限差分数值模拟[J].石油物探,2008,47(2):123-128 Sun C Y,Li S J,Ni C K,et al.Elastic wave modeling on a variable gird finite-difference method[J].Geophysical Prospecting for Petroleum,2008,47(2):123-128

[12] 黄超,董良国.可变网格与局部时间步长的交错网格高阶差分弹性波模拟[J].地球物理学报,2009,52(11):2870-2878 Huang C,Dong L G.Staggered-grid high-order finite-difference method in elastic wave simulation with variable grids and local time-steps[J].Chinese Journal of Geophysics,2009,52(11):2870-2878

[13] 朱生旺,曲寿利,魏修成,等.变网格有限差分弹性波动方程数值模拟方法[J].石油地球物理勘探,2007,42(6):634-639 Zhu S W,Qu S L,Wei X C,et al.Numeric simulation by grid-various finite-difference elastic wave equation[J].Oil Geophysical Prospecting,2007,42(6):634-639

[14] 李振春,李庆洋,黄建平,等.一种稳定的高精度双变网格正演模拟与逆时偏移方法[J].石油物探,2014,53(2):127-136 Li Z C,Li Q Y,Huang J P.A stable and high-precision dual-variable grid forward modeling and reverse time migration method[J].Geophysical Prospecting for Petroleum,2014,53(2):127-136

[15] 王守东.声波方程完全匹配层吸收边界[J].石油地球物理勘探,2003,38(1):31-34 Wang S D.Absorbing boundary condition for acoustic wave equation by perfectly matched layer[J].Oil Geophysical Prospecting,2003,38(1):31-34

[16] 陈可洋.声波完全匹配层吸收边界条件的改进算法[J].石油物探,2009,48(1):76-79 Chen K Y.The improvement of perfect matched layer absorbs condition[J].Geophysical Prospecting for Petroleum,2009,48(1):76-79

[17] 陈可洋.完全匹配层吸收边界条件研究[J].石油物探,2010,49(5):472-477 Chen K Y.The research of perfect matched layer condition[J].Geophysical Prospecting for Petroleum,2010,49(5):472-477

[18] 吴国忱,王华忠.波场模拟中的数值频散分析与校正策略[J].地球物理学进展,2005,20(1):58-65 Wu G C,Wang H Z.Analysis of numerical dispersion in wave-field simulation[J].Progress in Geophysics,2005,20(1):58-65

[19] 刘洋,李承楚,牟永光.任意偶数阶精度有限差分法数值模拟[J].石油地球物理勘探,1998,33(1):1-10 Liu Y,Li C C,Mou Y G.Finite-difference numerical modeling of any even-order accuracy[J].Oil Geophysical Prospecting,1998,33(1):1-10

附录A

加入衰减项的PML方程为:

(A1)

将时间导数的二阶中心差分格式代入公式(A1):

(A2)

整理并求解这个方程组,得到双相介质弹性波PML起始方程:

(A3)

其中,

(A4)

将方程(A4)依照求导方向拆分,加入不同方向的衰减系数,利用二阶空间偏导的M阶差分格式进行离散近似即可得到双相介质弹性波方程的PML差分格式。

以x方向为例,空间二阶偏导数的M阶精度常规差分格式为[15]:

(A5)

式中:cm为差分系数。

空间二阶混合偏导数的M阶精度常规差分格式为[17]:

(A6)

对于x方向,有:

(A7)

其中,

(A8)

对z方向也有相似的结论。

对于x,z方向:

(A9)

其中,

(A10)

附录B

以x方向过渡区的第n个点为例,当大小网格步长比为α时,空间M阶可变网格差分格式为[9]:

(B1)

同理得到z方向的过渡差分格式。

x,z方向的混合偏导数的过渡问题可以转化为求解两个嵌套的一阶导数问题,即:

(B2)

同理,过渡区的二阶混合偏导数也可以通过两次嵌套的一阶导数过渡差分格式求解。即:

(B3)

则基于PML边界过渡区的时间二阶、空间M阶精度声波方程可变网格差分格式为:

(B4)

其中,

(B5a)

(B5b)

(B5c)

(B5d)

(B5e)

(B5f)

(B5g)

(B5h)

(B5i)

(B5j)

(B5k)

(B5l)

(B5m)

(编辑：陈 杰)

A variable grid finite-difference scheme with PML boundary condition in elastic wave of porous media

Sun Linjie,Liu Chuncheng,Zhang Shixin

(CNOOCResearchInstitute,Beijing100028,China)

In order to improve the accuracy of forward modeling in porous media,a grid variation finite-difference simulation method is applied to Biot’s two-phase elastic wave equation.The difference approximation schemes in grid-variation zone for second-order mixed partial derivative are solved and the variable-grid finite difference scheme with PML boundary is derived,which realizes the two-phase media elastic wave variable-grid forward modeling with integral-multiple variable spatial and time grid steps.Numerical tests show that the grid step variation method would improve the simulation accuracy by using smaller gird step to resample the subtle geological structure and the area with rapid change of geological conditions.Moreover,the algorithm can also ensure the computational efficiency by suppressing the sampling rate to the region with relatively stable model parameters.Compared with conventional forward modeling method,the numerical testing result indicates that the two-phase variable-grid forward modeling method obviously improves the simulation accuracy and efficiency.

Biot theory,porous media,PML boundary condition,variable grid,finite difference

2015-03-30;改回日期：2015-07-08。

孙林洁(1987—),女,工程师,主要从事地震储层预测研究工作。

国家科技重大专项“海洋深水区油气勘探关键技术”项目(2011ZX05025-001)资助。

P631

A

1000-1441(2015)06-0652-13

10.3969/j.issn.1000-1441.2015.06.003