含不连通孔隙的致密砂岩储层岩石弹性模量预测方法

刘 倩,印兴耀,李 超

(中国石油大学(华东)地球科学与技术学院,山东青岛266580)

含不连通孔隙的致密砂岩储层岩石弹性模量预测方法

刘 倩,印兴耀,李 超

(中国石油大学(华东)地球科学与技术学院,山东青岛266580)

致密砂岩储层与常规储层相比具有低孔、低渗、连通性差等特性。针对致密砂岩储层中不连通孔隙的影响,提出了一种适用于致密砂岩储层的岩石物理模型建立方法,重点是利用Raymer公式引入不连通孔隙度的影响来修正基质模量的方法,阐述了依照连通孔隙度Gassmann方程在干岩石骨架的孔隙空间进行流体充填,分析讨论了不连通孔隙的引入对于岩石弹性模量及流体响应特征的影响。应用该方法对实验测量数据及某实际工区井资料进行试算发现,与常规有效介质模型预测结果相比,基于含不连通孔隙致密砂岩岩石物理模型估算的纵、横波速度值与测井结果吻合更好,验证了方法的合理性。

致密砂岩;不连通孔隙;岩石物理;Gassmann方程

随着非常规油气勘探开发程度的深入,致密砂岩储层所占的比例越来越高。与常规储层相比,致密砂岩储层的物性差,孔隙度较低,一般小于10%,孔隙结构复杂,孔隙连通性和渗透性较差。在常规砂岩储层中,有效的连通孔隙度通常只比总孔隙度稍低,而在致密砂岩储层中,强烈的成岩作用导致有效孔隙度值比总孔隙度要小很多,不连通孔隙增多,一般有效孔隙度占总孔隙度的40%～75%[1],因此不连通孔隙度的影响不能忽视。

通常,基于理论研究的需要,需对真实岩石组分关系加以简化,使其可用一定的模型来表征实际介质的基本特征,因此岩石物理建模是岩石物理研究中的基础问题[2-7]。目前应用较多的求取岩石弹性模量的模型有7种:Greenberg-Castagna,Cemented,MudRock,Unconsolidated,Critical-porosity,Krief和Xu-White模型。总体而言,前面4个模型主要适用于中等或中高孔隙地层,后3种模型主要适用于中等或中低孔隙地层[8-11]。由于致密砂岩与常规储层相比具有低孔、低渗以及孔隙结构复杂等特性[4],因此应用常规的岩石物理理论模型和方法难以进行有效的储层预测,无论在实验室分析、测井解释还是地震反演过程中,均会因岩石物理参数偏差而导致整个致密砂岩气藏评估的不确定性。

目前,很多学者进行了有关致密砂岩岩石物理建模方面的研究。孙晟等[12]修正Hashin-Strikman边界理论,弥补了孔隙度小于20%时对弹性模量尤其是剪切模量估算的不足。Ruiz等[13]采用Berryman自相容模型进行致密砂岩岩石物理建模研究并预测致密砂岩弹性模量。Yan等[14]采用Mori-Tanaka模型,对四川盆地低孔砂岩进行孔隙纵横比和弹性模量的估算。但是这些理论模型也没有考虑致密储层中不连通孔隙的影响。

本文针对致密砂岩储层的低孔、低渗特点,从岩石的内在机理出发,利用孔隙度分离原理,首先应用Raymer公式引入对不连通孔隙度的描述,修正基质的弹性模量,然后基于改进的连通孔隙Gassmann方程[15]计算饱和岩石等效弹性模量,建立了含不连通孔隙结构的岩石物性参数与弹性模量之间的定量关系,实现了等效弹性模量参数的求取,刻画了致密储层的岩石物理特征。基于新模型反演得到不连通孔隙度的值可有效预测致密砂岩储层纵、横波速度,并在一定程度上反映岩石孔隙的连通情况。

1 方法原理

致密砂岩岩石物理模型构建的基本思想是:按照弹性介质理论,在假设致密砂岩孔隙的特征尺度远远小于地震波波长的前提下,考虑不连通孔隙对基质模量的影响,通过等效介质理论计算骨架模量,利用Gassmann方程在连通孔隙中充填流体,构建根据岩石矿物、孔隙流体组成以及孔隙特征的岩石物理模型。这个模型的主要特点是把岩石体积模量与岩石骨架模量、岩石组成矿物的弹性模量、孔隙流体的弹性模量以及孔隙度有机联系在一起,由此可实现对复杂多孔介质流体饱和岩石等效弹性模量的估算。

1.1 有效介质理论

很多有效介质理论(如:自相容模型(SC模型)或微分等效介质模型)可以用来估算岩石的弹性模量[13]。本文主要应用Berryman提出的SC模型[16]进行分析。N相混合物的自相容近似的一般形式为:

(1)

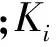
(2)

式中:张量Tiijj和Tijij与背景介质弹性模量和孔隙纵横比参数有关,具体表达式可参见文献[16]。

由于有效介质理论均假设流体不能互相流动,因此这种方法模拟的是高频下饱和岩石的属性,且认为包含物彼此之间是隔离的。在低频时,当波动引起的孔隙压力增加有充分时间通过液体流动而平衡压力时,需要利用有效介质理论先求取干燥岩石的等效模量,再用Gassmann理论((3)式)[17]来添加流体的影响。而根据Gassmann理论的假设条件,则认为所有孔隙都是连通的，即：

(3)

式中：Km表示岩石基质体积模量;Kf表示孔隙流体的体积模量;Kdry和μdry分别表示干燥岩石的体积模量和剪切模量;Ksat和μsat分别表示饱和岩石的体积模量和剪切模量；φ表示岩石孔隙度。

1.2 基于孔隙度分离的弹性模量计算

根据致密储层含不连通孔隙的特点,在常规的有效介质和Gassmann理论建模的基础上,引入一个新的变量,即不连通孔隙度。将岩石的总孔隙度φt分成连通孔隙度φc和不连通孔隙度φd[18]:

(4)

其中,连通的孔隙是指与其它孔隙相互连接的孔隙,是渗透性孔隙,并认为流体流动只发生在连通孔隙中;不连通孔隙是指与其它孔隙不连通的孔隙,是非渗透性孤立孔隙(图1)。本文中不连通孔隙既包括泥质颗粒间的束缚水又包括砂岩颗粒间的非有效孔喉空间,根据其孔隙结构特征、孔隙连通性以及孔隙间的相互作用关系,可以将其看作是嵌入岩石基质矿物的孔隙。

孔隙度分离首先应用速度-孔隙度经验公式在基质中添加不连通孔隙的影响。应用Raymer-Hunt-Gardner关系[11]在已知基质矿物和不连通孔隙流体的情况下估测含不连通孔隙的基质模量。首先用公式(5)计算含不连通孔隙岩石基质的纵波速度,应用Raymer扩展公式[19]((6)式)估测其横波速度。

(5)

(6)

式中:vPS,vSS为修正的岩石基质的纵、横波速度;vPm,vSm为岩石基质初始纵、横波速度,可由基质组成矿物的模量计算得到;vPf为不连通孔隙中流体的纵波速度,通常认为不连通孔隙中含有不可流动的地层水[20];φd为不连通孔隙度,φd=φt-φc;ρm为初始基质矿物的密度;ρfl为不连通孔隙中流体的密度。

由修正岩石基质的速度值,通过(7)式可以得到修正岩石基质(含不连通孔隙)的有效压缩模量Cs和剪切模量μs。

(7)

式中:ρms为修正基质矿物的密度。

(8)

不连通孔隙是不能与外界进行流体交换的孔隙,这类孔隙很难发生流体流动和流体替换。Gassmann提出方程的重要假设条件之一是所有孔隙都连通。而当孔隙系统中出现了孤立的不连通孔隙时,为了保证这个理论能够合理有效的应用,需要应用连通孔隙的概念,并将不连通孔隙看作是固体基质的一部分。因此,孔隙度分离需要考虑不连通孤立孔隙的同时,根据连通孔隙的流体替换方程,计算流体饱和岩石的体积模量、剪切模量,即：

(9)

(10)

假设不连通孔隙中完全饱和水,所有油或气包含于连通的孔隙中。在已知不连通孔隙度φd,总孔隙度φt和含水饱和度Sw的条件下,可得连通孔隙中含油(或气)饱和度为:

(11)

则连通孔隙中含水饱和度为:

(12)

由此可以看出,当岩石中的水全部存在于不连通孔隙中时,Swe变为0。则(9)式中混合流体的体积模量为:

(13)

式中:Kw,KH分别为水、油(或气)的体积模量。

渗透率是表征岩石孔隙间流体流动能力的重要参数之一。影响渗透率的因素很多,其大小取决于岩石孔隙的大小、形状与连通情况等,即与孔隙结构有密切关系。本文利用孔隙度分离原理,将总孔隙度分成连通和不连通的孔隙度,则连通孔隙度的大小可以表示岩石的连通情况,进而在一定程度上反映孔隙流体的流动能力。在实际应用中,不连通孔隙度也可作为可调节变量进行实测与预测速度的匹配。这里的渗透率忽略了Biot局部流的影响,也不需要对衰减效应进行修正。

2 模型参数分析

2.1 不连通孔隙对模量的影响

为了解含不连通孔隙模型中饱和模量的变化情况,首先应用本文提出的含不连通孔隙的新模型进行饱和模量的计算,再分别应用SC+Gassmann方程与SC模型计算饱和模量值(图2)。相对于应用SC+Gassmann方程的常规方法,本文提出的新模型利用孔隙度分离原理在基质中加入了不连通孔隙的影响,并利用Gassmann方程在连通的孔隙中添加流体。模型计算过程中矿物组成与流体参数如表1所示。

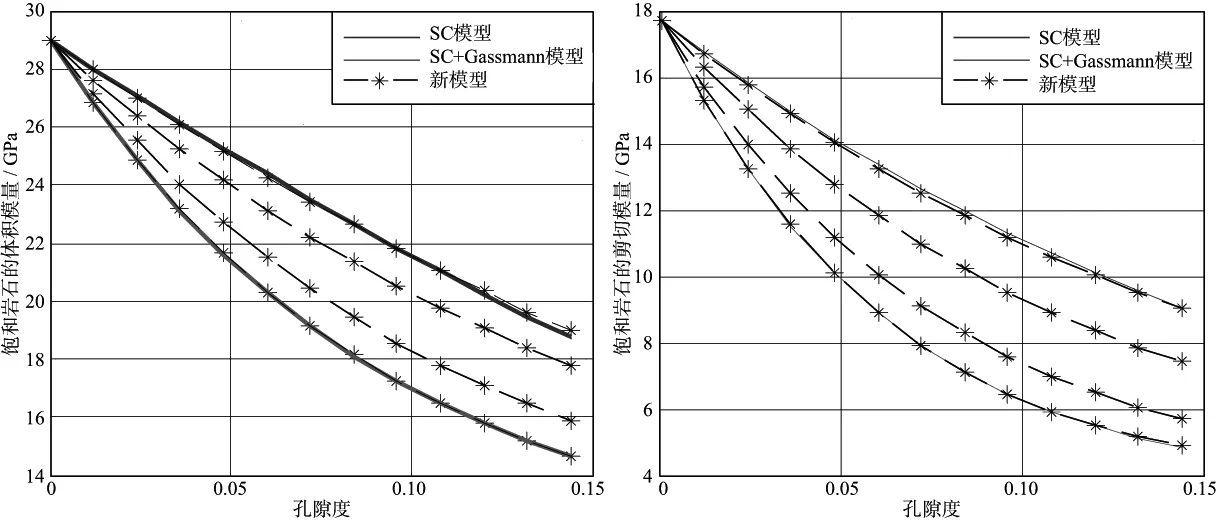
图2 饱和模量随总孔隙度的变化结果

表1 模型计算过程中矿物组分与流体参数

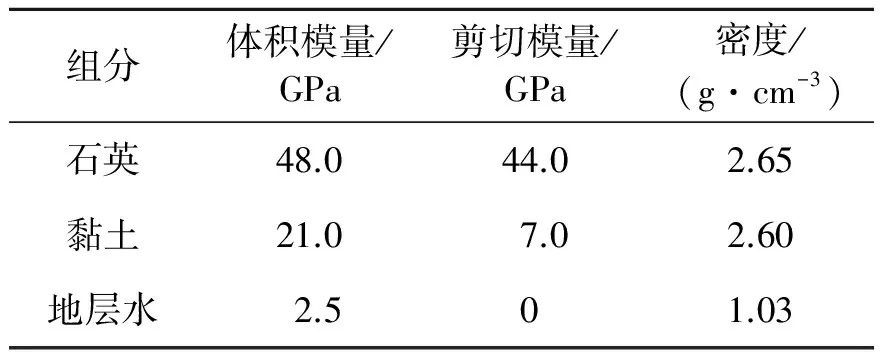
组分体积模量/GPa剪切模量/GPa密度/(g·cm-3)石英48．044．02．65黏土21．07．02．60地层水2．501．03

图2中,玫红色线表示应用SC+Gassmann方程计算饱和模量的结果,蓝色线表示应用SC模型计算饱和模量的结果,星号点表示新模型的计算结果,且由上至下,不连通孔隙度对于总孔隙度的比值逐渐减小,其值分别为:1.0,0.7,0.3,0。从图2中可以看出,饱和模量随着总孔隙度的增加而降低;本文提出的新模型随着不连通孔隙的相对增加,饱和模量值降低。当不连通孔隙度为0时,即孔隙全连通时,本文提出的新模型计算结果与常规SC+Gassmann方程计算的结果相同;而当不连通孔隙度与总孔隙度值相同时,即所有孔隙为孤立不连通孔隙时,本文提出的新模型的计算结果与描述孤立包含物的SC模型的结果相同。因此,新模型通过引入不连通孔隙度的概念,将低频和高频饱和模量(分别对应孔隙全连通与孤立的情况)的计算结果联系起来,从而更好地描述低孔隙度、孔隙连通性差的致密砂岩储层含流体饱和模量的变化。

2.2 连通孔隙中流体的影响

为了测试不同流体对地震振幅的影响,构建了一个如图3所示的伪井曲线,其中包含一段致密砂岩储层。首先假设初始储层总孔隙度为10%,不连通孔隙度为3%,含水饱和度为100%,如图3中实线所示。我们需要求取流体替换后含气饱和度为20%同一储层的地震响应,图3中蓝色虚线表示用本文提出的含不连通孔隙的新模型计算的结果,红色点划线表示用常规Gassmann模型计算的结果。考虑到基质中不连通孔隙内流体不能流动,在进行流体替换计算时,不对该类孔隙内流体进行替换。

图3显示了初始致密砂岩的性质和流体替换后的弹性性质。可以看到,当储层中含有20%气时,依据构建的含有不连通孔隙的岩石物理模型,纵波波阻抗和泊松比相对常规方法有显著的变化,而横波基本没有出现变化。常规方法对于阻抗和泊松比的预测值减小量相对小,而考虑不连通孔隙的方法,显著降低了阻抗及泊松比的值。

用计算出的伪井结果与40Hz的雷克子波褶积,可得到合成的角度道集,如图4所示。结合图5 中振幅反射系数随角度的变化关系,可以观察到100%含水致密砂岩储层表现出第Ⅰ类AVO现象,而用常规模型计算的流体替换后20%含气砂岩仍保持第Ⅰ类AVO现象,但是用本文提出的考虑不连通孔隙模型计算的结果,出现了第Ⅱ类AVO现象。而对于替换流体为油的情况,AVO的类型并不会发生改变。

图3 含致密储层段的伪井曲线

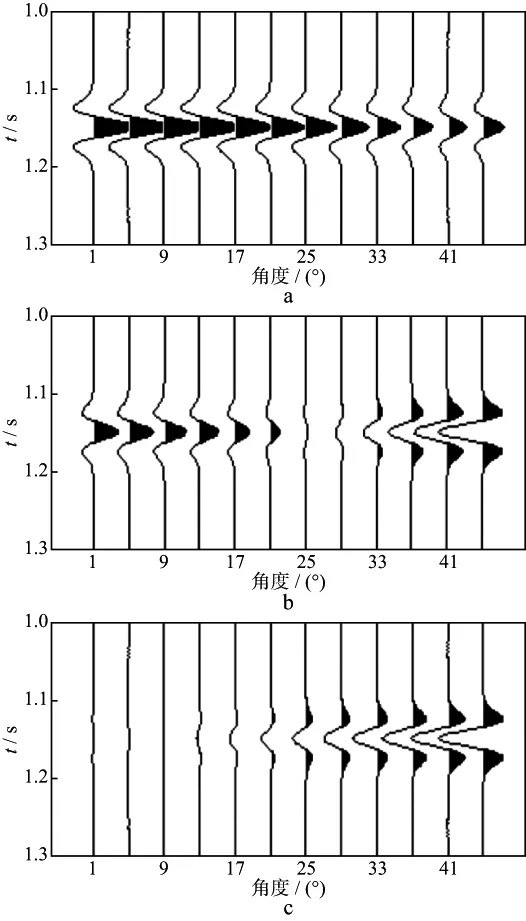
图4 合成的角度道集

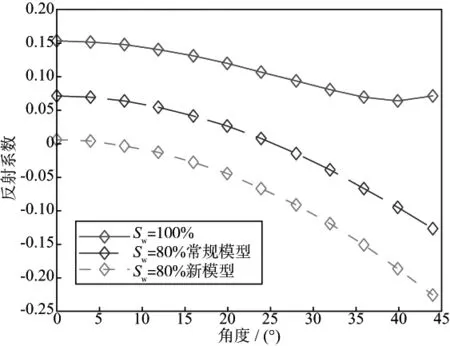
图5 反射系数随角度变化结果

3 应用效果分析

含不连通孔隙模型中,岩石基质和岩石骨架的弹性模量都受到不连通孔隙的影响,也就是说,不连通孔隙可以影响岩石的弹性模量,进而会影响岩石的纵、横波速度。因此,岩石的纵、横波速度都与不连通孔隙度有关。所以就可以利用岩石的不连通孔隙度作为纽带,应用岩石物理模型来重构纵、横波速度。纵、横波速度与模量的关系为:

(14)

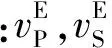
在岩石物理建模过程中,岩石的总孔隙度一般可通过测井资料计算得到,但是模型中不连通孔隙度的值不容易实际测量得到。这里根据已知的测井资料,将模型中的不连通孔隙度看作一个变量,利用纵波速度作为约束条件,建立目标函数((15)式),利用模拟退火的优化方法寻找使得目标函数取最小值的φd作为不连通孔隙度值,再应用建立的新模型进行纵、横波速度的重构。

(15)

首先分别利用Han等[21]及Tutuncu等[22]的实验室测量数据对上述速度估算方法进行测试,文中所选用的数据:①是Han测量得到的10个水饱和致密砂岩参数;②是Tutuncu测量得到的SFE#1井的9个水饱和致密砂岩参数。图6是纵、横波速度估算结果及误差绝对值。图6a和

图6b 显示纵波速度预测结果,从反演的相对误差分布图中可以看出,有近90%的样品预测相对误差小于2.5%,10%的样品预测相对误差为2.5%～5.0%,从计算与实测的纵波速度看,能如实的反映实际值,预测精度相对较高。图6c和图6d 显示横波速度预测结果,可见结果不如纵波预测结果精度高,从反演的相对误差分布图中可以看出,有近70%的样品预测相对误差小于2.5%,30%的样品预测相对误差为2.5%～5.0%,从计算与实测的横波速度看,能如实地反映实际值。

选取某致密砂岩工区的A井为例,该工区储层为低孔、低渗储层,且储层中主要含气。依据建立的岩石物理模型调节不连通孔隙度所占的比例,计算致密砂岩储层的纵、横波速度与测井数据进行对比分析,并与常规应用SC模型计算干岩石骨架模量并利用Gassmann方程计算饱和岩石模量方法(不进行孔隙度分离)的计算结果进行对比,以此检验本文方法的应用效果。

图7显示了不连通孔隙度反演结果。图中,蓝色曲线表示总孔隙度,红色曲线表示不连通孔隙度。从图7中可以看出,在孔隙度较大、物性较好的储层(如:4243～4248m;4260～4275m)中,不连通孔隙占总孔隙的体积分数相对较低。图8为采用不同模型估测的纵、横波速度及其与实测结果的误差。图8a和图8c中红色曲线代表本文提出模型估算的速度,蓝色曲线代表测井真实值;图8e 中绿色曲线代表采用SC+Gassmann模型估算的横波速度,蓝色曲线代表测井真实值。从图8a 至图8d可以看出,通过含不连通孔隙岩石物理模型计算的纵波速度和横波速度与实测结果相差不大。从图8c至图8f可以看出,相比SC+Gassmann模型估算的横波速度,由于考虑不连通孔隙的影响,本文新模型预测的速度与实测结果相比误差更小,这也进一步说明考虑不连通孔隙进行岩石物理模型构建流程符合要求,也与致密砂岩储层的特点更吻合。这里反演的不连通孔隙度值和岩石的实际不连通孔隙度值有一定的不符,但可以在一定程度上反映岩石的不连通性,而随着模型中其它参数精度的提高,不连通孔隙度值应该接近于实际情况。

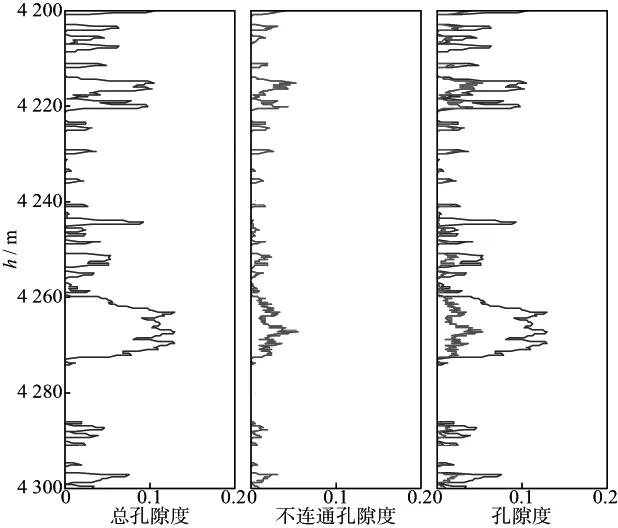
图7 不连通孔隙度反演结果

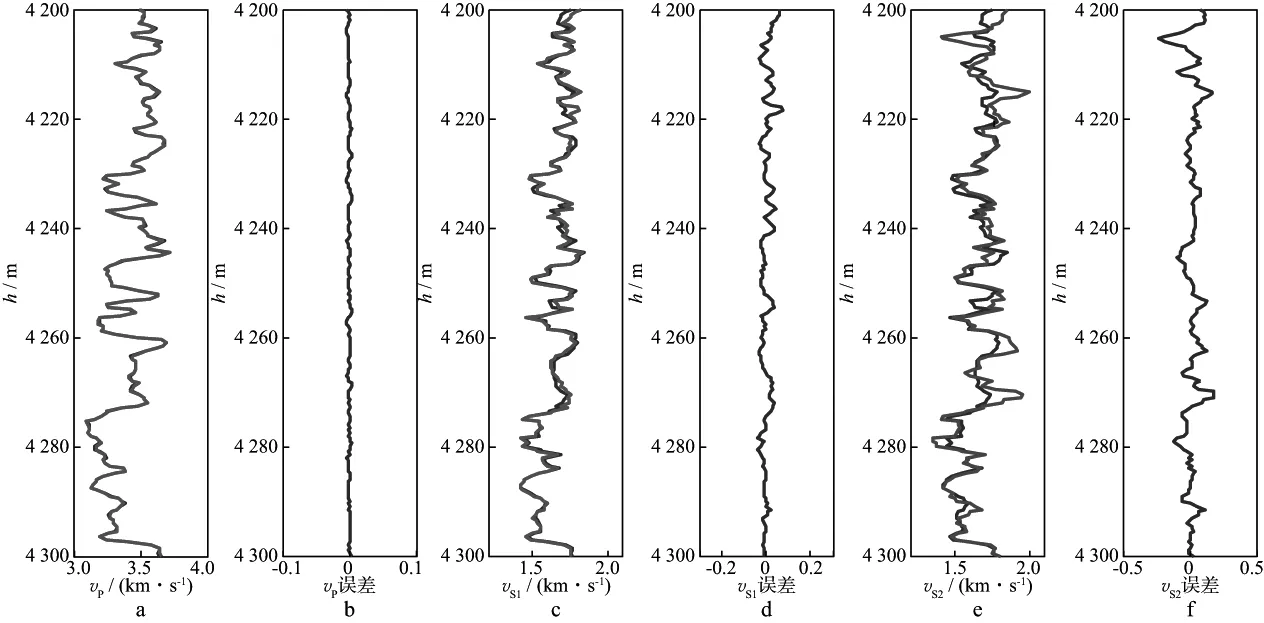
图8 采用不同模型估算的纵、横波速度以及与实测结果的误差

4 结论

针对致密砂岩低孔条件下不连通孔隙的影响,本文提出了适用于致密砂岩储层的岩石物理模型建立流程。建立了低孔条件下含不连通孔隙的矿物骨架、混合流体和等效弹性参数之间的联系,实现了有效弹性模量的定量计算。Raymer经验公式由于不考虑复杂的孔隙结构特征参数,是一种简单有效的基质模量修正方法。对于饱和模量的计算,本文提出的新模型通过引入不连通孔隙度这一新变量可将有效介质模型与Gassmann模型联系起来。在低孔、低渗含气致密砂岩储层中,基于新模型的连通孔隙流体替换会引起弹性参数的显著变化,从而造成AVO类型的转变。

结合实际测井资料进行对比可知,理论方法模拟的结果和实际测井数据两者吻合得比较好,说明了基于含不连通孔隙的致密砂岩岩石物理模型的可靠性。因此,考虑不连通孔隙度的方法可以有效地分析岩石的孔隙结构,更好地预测致密储层的弹性模量,基于新模型建立的等效弹性模量定量关系也为岩石的纵、横波速度预测提供了可靠的物理基础。

[1] North F K.Petroleum geology[M].Boston:Allen & Unwin,1985:1-607

[2] 马淑芳,韩大匡,甘利灯,等.地震岩石物理模型综述[J].地球物理学进展,2010,25(2):460-471 Ma S F,Han D K,Gan L D,et al.A review of seismic rock physics models[J].Progress in Geophysics,2010,25(2):460-471

[3] 徐胜峰,李勇根,曹宏.地震岩石物理研究概述[J].地球物理学进展,2009,24(2):680-691 Xu S F,Li Y G,Cao H.A review of seismic rock physics[J].Progress in Geophysics,2009,24(2):680-691

[4] 印兴耀,刘欣欣,曹丹平.基于 Biot 相洽理论的致密砂岩弹性参数计算方法[J].石油物探,2013,52(5):445-451 Yin X Y,Liu X X,Cao D P.Elastic parameters calculation method of tight sand based on Biot self-adaption theory[J].Geophysical Prospecting for Petroleum,2013,52(5):445-451

[5] 刘欣欣,印兴耀,张峰.一种碳酸盐岩储层横波速度估算方法[J].中国石油大学学报:自然科学版,2013,37(1):42-49 Liu X X,Yin X Y,Zhang F.S-wave velocity estimation method in carbonate reservoir[J].Journal of China University of Petroleum(Edition of Natural Sciences),2013,37(1):42-49

[6] 白俊雨,宋志翔,苏凌,等.基于 Xu-White 模型横波速度预测的误差分析[J].地球物理学报,2012,55(2):589-595 Bai J Y,Song Z X,Su L,et al.Error analysis of shear-velocity prediction by the Xu-White model[J].Chinese Journal of Geophysics,2012,55(2):589-595

[7] 张广智,陈怀震,王琪,等.基于碳酸盐岩裂缝岩石物理模型的横波速度和各向异性参数预测[J].地球物理学报,2013,56(5):1707-1715 Zhang G Z,Chen H Z,Wang Q,et al.Estimation of S-wave velocity and anisotropic parameters using fractured carbonate rock physics model[J].Chinese Journal of Geophysics,2013,56(5):1707-1715

[8] Castagna J,Batzle M.Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks[J].Geophysics,1985,50(4):571-581

[9] Greenberg M,Castagna J.Shear-wave velocity estimation in porous rocks:theoretical formulation,prelimulation,preliminary verification and applications[J].Geophysical Prospecting,1992,40(2):195-209

[10] Xu S,White R.A new velocity model for clay-sand mixtures[J].Geophysical Prospecting,1995,43(1):91-118

[11] Mavko G,Mukerji T,Dvorkin J.The rock physics handbook:tools for seismic analysis of porous media[M].Cambridge:Cambridge University Press,2009:90-121,187-211

[12] 孙晟,牛滨华,李佳.Hashin-Shtrikman弹性模量边界的转换[J].中国石油大学学报(自然科学版),2007,31(2):45-50 Sun S,Niu B H,Li J.The conversion of Hashin-Shtrikman elastic modulus boundary[J].Journal of China University of Petroleum(Edition of Natural Sciences),2007,31(2):45-50

[13] Ruiz F,Cheng A.A rock physics model for tight gas sand[J].The Leading Edge,2010,29(12):1484-1489

[14] Yan X F,Yao F C,Cao H,et al.Analyzing the mid-low porosity sandstone dry frame in central Sichuan based on effective medium theory[J].Applied Geophysics,2011,8(3):163-170

[15] Dvorkin J,Mavko G,Gurevich B.Fluid substitution in shaley sediment using effective porosity[J].Geophysics,2007,72(3):O1-O8

[16] Berryman J G.Long-wavelength propagation in composite elastic media II:ellipsoidal inclusions[J].The Journal of the Acoustical Society of America,1980,68(6):1820-1831

[17] Gassmann F.Uber die elastizitat poroser Medien[J].Vierteljahrsschrift der Natruforschenden Gesellschaft Zurich,1951,96:1-23

[18] Aljarrah F.Methods of fitting compressional and shear wave velocities versus saturation curves and the interpretation of laboratory velocity measurements in partially saturated rocks[D].Houston:University of Houston,2009

[19] Dvorkin J P.Yet anothervSequation[J].Geophysics,2008,73(2):E35-E39

[20] Carcione J M,Gurevich B,Cavallini F.A generalized Biot-Gassmann model for the acoustic properties of shaley sandstones[J].Geophysical Prospecting,2000,48(3):539-557

[21] Han D,Nur A,Morgan D.Effects of porosity and clay content on wave velocities in sandstones[J].Geophysics,1986,51(11):2093-2107

[22] Tutuncu A N,Podio A L,Sharma M M.An experimental investigation of factors influencing compressional-and shear-wave velocities and attenuations in tight gas sandstones[J].Geophysics,1994,59(1):77-86

(编辑：顾石庆)

Rock elastic modulus estimation for tight sandstone reservoirs with disconnected pores

Liu Qian,Yin Xingyao,Li Chao

(SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China)

Tight sandstone is characterized by low-porosity,low-permeability and poor-connectivity,which is different from the conventional reservoirs.This paper proposes a method to build rock physical model for tight sandstone reservoirs due to the properties of disconnected pores and its impact.The method focuses on introducing the disconnected pores using Raymer relations to modify the matrix elastic modulus,and it also aims to accomplish fluid filling work using Gassmann equation with effective porosity.Then quantitative analysis is carried out to calculate the elastic modulus in tight sandstones saturated with fluids.Moreover,it analyzes the sensitivity of the rock elastic parameters for fluid.Finally,we discuss the accuracy of the parameters estimation based on rock physical model considering disconnected pores.The estimated S-wave velocity is consistent with the experimental measurement data and the log value,which proves the rationality of the method.

tight sandstone,disconnected pores,rock physics,Gassmann equation

2015-01-29;改回日期：2015-05-27。

刘倩(1988—),女,博士在读,主要从事岩石物理及地震波场模拟方面的研究。

国家重点基础研究发展计划(973计划)项目(2013CB228604)资助。

P631

A

1000-1441(2015)06-0635-08

10.3969/j.issn.1000-1441.2015.06.001