漂浮式风力机驳船式平台响应特性分析
丁勤卫, 李 春,2, 成 欣, 叶 舟,2
(1.上海理工大学能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093)
漂浮式风力机驳船式平台响应特性分析
丁勤卫1, 李 春1,2, 成 欣1, 叶 舟1,2
(1.上海理工大学能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093)
平台的稳定是海上漂浮式风力机能够安全运行的最基础保障.通过建立基于驳船式平台的海上风力机整机模型,采用有限元方法,研究了漂浮式风力机驳船式平台在风、浪、流3种环境载荷联合作用下的时频域动态响应.通过漂浮式风力机驳船式平台在时域和频域内的变化幅度来分析平台的动态响应特性,得到了波浪力即F-K力和绕射力对平台六自由度运动的贡献以及各波浪力随频率的变化趋势.结果表明:平台幅值响应算子和平台所受波浪力均在低频波浪作用下出现较大响应;平台在纵荡、垂荡和纵摇方向的运动响应较之其他3个方向更加明显.
漂浮式风力机;驳船式平台;动态响应
因煤、石油和天然气等化石能源的逐渐消耗,环境污染问题日益突出,风能作为一种清洁的永续能源逐渐受到各国的重视[1].与陆地相比,海上有着更为丰富的风能资源、更为广阔平坦的区域,这使得海上风力发电成为近年来风电行业的热点[2-4].海上漂浮式风力机同时要受到海风、海浪和海流等多种环境载荷的作用,导致风力机动态响应的复杂性,进而影响风力机的稳定工作.同时,漂浮式平台作为海上漂浮式风力机的支撑结构,其稳定性是漂浮式风力机安全运行的最基础保障.因此,对漂浮式风力机平台在风浪流载荷联合作用下动态响应特性的研究,将为海上风力机安全稳定工作评判提供理论可行性参考[5].
漂浮式风力机平台根据其获取静态稳定性的不同可分为3种基本类型:浮柱式(Spar)平台、张力腿(tension leg platform,TLP)平台、驳船式(Barge)平台.上述3种平台稳定性的来源分别为:压舱物的回复力矩、张力筋腱的预张力和水线面的面积矩,但实际情况一般为3种方式的组合.3种漂浮式平台各有优缺点:Spar平台受波浪影响较小,但吃水深度较大,难以在普通港口制造和安装,同时Spar平台因其较大的自由度而需要更多的压舱物来配重,因此导致了整个平台系统成本增高.TLP平台系泊系统采用了有一定预张力的张力筋腱,因而稳定性相对于其他类型平台较好,但成本很高.Barge平台可被简化为没有重量的浮箱,其较大的水面积矩可提供足够的恢复力矩,足以保证整个平台系统在各种海况下不倾覆.同时就目前的制造水平而言,Barge平台单位重量成本最低,结构相对简单,而且由于较为成熟的造船技术也可进一步降低制造成本.因此,本文漂浮式风力机平台选择Barge平台.
根据海洋石油平台的相关规范和经验,目前国内外学者对漂浮式风力机平台性能已展开了相关探索[6].2006年,Vijfhuizen[7]设计了一个基于驳船式平台的5 MW的风力发电机系统,其特点是可以结合其他形式海洋能源进行发电.Wayman[8]考虑动力学与经济性两方面因素,对比了TLP平台和驳船平台的5 MW漂浮式风力发电机组在不同的海况下,整个系统的年发电量.Wayman等[9]对MIT/ NREL浅水驳船和MIT/NREL TLP平台模型性能进行经济性对比计算.Sebastian等[10]简单求解了ITI能源驳船风力机气动力学性能.
本文建立基于驳船式平台的漂浮式风力机整机模型,运用有限元软件ANSYS中的水动力学模块对其进行频域和时域特性分析,研究其在风浪流载荷联合作用下的动态响应.
1 环境载荷
漂浮式风力机系统所受的环境载荷源自风、浪、流、地震等许多因素的作用[11].本文为简化计算且不失一般性,仅考虑风、浪、流3种载荷.
1.1 风载荷
海上风能具有更高的年平均速度、更低的湍流、更低的风剪切等特点.其次,海上风力机整体结构非常高,承受更大的风载.因此,对于海上漂浮式风力机,风对其产生更重要的影响.海上漂浮式风力机气动载荷包括:风轮推力、风轮扭矩、塔架所受风推力及其对整机的倾覆力矩.风轮推力T和风轮扭矩M的计算公式为
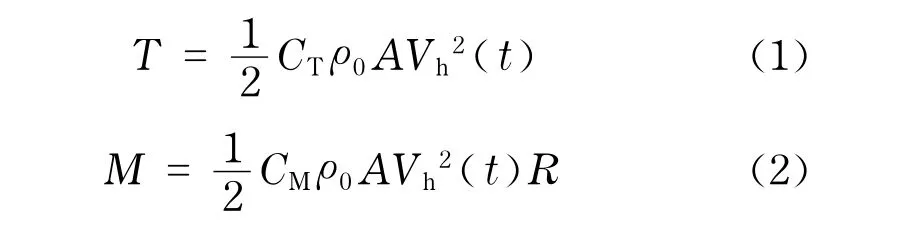
式中,CT为推力系数;ρ0为空气密度;A为风轮旋转面积;Vh(t)为塔架高度h处的瞬时风速;CM为俯仰力矩系数;R为风轮半径.
塔架所受风推力Ft及其对整机产生的倾覆力矩Mt计算公式为
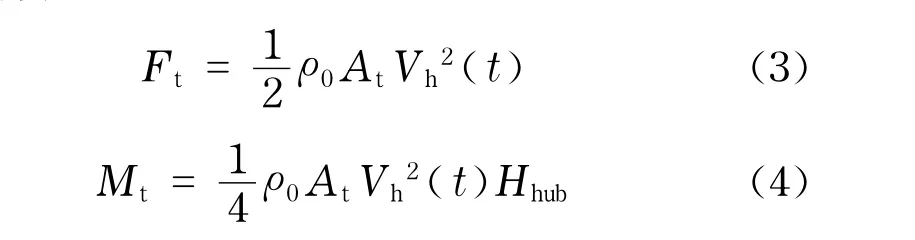
式中,At为风吹至塔架时的投影面积;Hhub为风力机轮彀高度.
1.2 波浪载荷
与陆上固定式风力机相比,海上漂浮式风力机的环境载荷条件更加复杂,主要是因为波浪载荷作用,波浪的作用是与陆上固定式风力机的最大不同之处.海工结构波浪载荷的计算使用的莫里森方程是依据结构物的存在对入射波没有显著影响这一基本假定建立的,即当结构物特征长度大于0.2倍的入射波波长时,绕射问题就会发生,此时莫里森方程不再适用.Barge平台特征尺度远大于0.2倍的入射波波长,平台的存在对入射波有显著扰动作用.因此,本文波浪载荷计算基于绕射理论.
海洋工程波浪载荷计算所使用的Morison方程是依据结构物的存在对入射波场没有显著影响这一基本假定建立的,当海洋结构物的特征长度大于0.2倍的波长时,绕射问题就会发生.本文采用辐射-绕射理论来求解浮体所受波浪载荷,在波浪作用下,定义流场中的速度势为
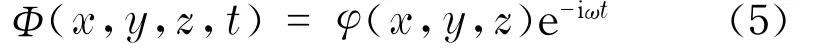
势函数φ被认为来自以下贡献:6个自由度上的辐射波浪势、入射波浪势和绕射波浪势.故势函数φ可进一步表示为
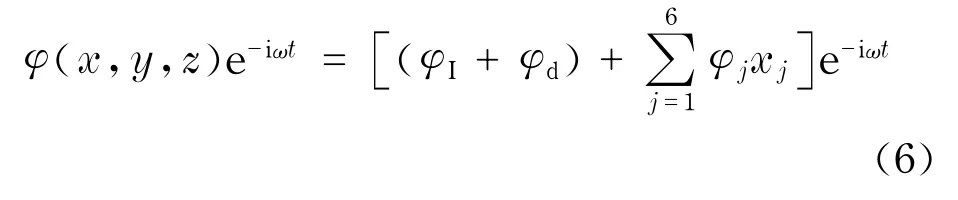
式中,φI为入射波浪势;φd为绕射波浪势;φj为浮体在第j个自由度上的运动引起的辐射波浪势;xj为浮体单位波幅下在第j个自由度上的位移;ω为入射波浪的圆频率.
根据线性化的伯努利方程由速度势求出一阶线性水压力梯度

由水压力分布,将水压力在浮体湿表面上积分便可求出波浪载荷.最后通过叠加不同波幅、波长和波向的规则波浪可得到不规则波浪中的结果.
规则波中的水动力问题通常可以分成以下两个问题来处理:
a.浮体以波激频率作刚体强迫振荡时的辐射力.
浮体本身作六自由度刚体强迫振荡时会产生辐射波.辐射波对结构物的作用即为辐射力,辐射力包括附加质量力和辐射阻尼力.附加质量力是浮体在流体中加速运动带动周围流体加速运动,流体的惯性对浮体的反作用力,由附加质量系数表征.辐射阻尼力是浮体在流体中运动时受到的阻尼力,由辐射阻尼系数表征.
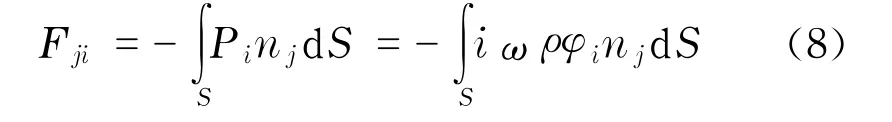
由于浮体强迫振荡而产生的辐射力可表示为式中,Fji表示单位波幅下浮体在第i个自由度上运动时在第j个自由度上的辐射力;Pi为第i个自由度上的水压力梯度;nj为第j个自由度对应的广义表面;S为浮体平衡位置处的湿表面;ρ为海水密度.

将速度势表示为实部和虚部的和,则式中,附加质量系数Aji和阻尼系数Bji分别为
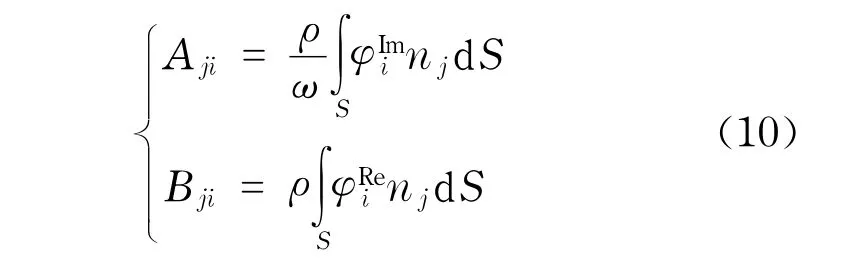
b.规则入射波对固定结构的作用.
结构物固定不动时的入射波作用,此时产生的波浪载荷称之为波浪激振力,包括F-K力和绕射力两部分.F-K力由未被扰动的入射波浪产生的动态压力场在浮体表面积分得到,其和绕射力共同组成规则入射波作用下浮体的非粘性力.当浮体尺寸较小时,波浪力只计算F-K力;而浮体尺寸较大时,波浪力还需计入绕射力加以修正.
规则入射波作用下的波浪激振力为

式中,Fj为单位波幅下第j个自由度上的波浪激振力.
1.3 海流载荷
海流一般可分为均匀流和剪切流两种类型.均匀流是指海流的流速大小和方向不会随着时间和水深的变化而发生变化,其值是固定的.剪切流是指海流的流速大小和方向随着时间和水深的变化而变化.实际海洋环境中,海流的大小随水深变化,因此海流可简化为剪切流.工程计算中,通常假定流速沿着水深方向呈线性变化或者二次曲线变化,海底流速几乎为零.浅水域流速通常处理为二次曲线变化,深水域流速通常处理为线性变化.本文驳船式平台漂浮式风力机设计水深150 m,属深水作业环境,故海流简化为线性变化.
对海工结构物,海流与结构物存在相互作用,海流运动相对缓慢和稳定,故考虑其作用时主要考虑其静力作用.海流对结构物的作用主要表现为水平拖曳力,单位高度的拖曳力为式中,AD为构件在与流速垂直平面上的投影面积; UC为距离海平面处深度h处海流速度;CD为阻力系数.

作用于整个构件的作用力总和为

2 建模与计算
2.1 驳船式平台及风力机整机模型
漂浮式平台为ITI Energy Barge,风力机模型为NREL 5MW风力机.表1和表2分别为平台及系泊系统详细参数和风力机详细参数[12].对应ITI Energy Barge平台参数和NREL 5MW风力机参数建立漂浮式风力机整机模型如图1所示.
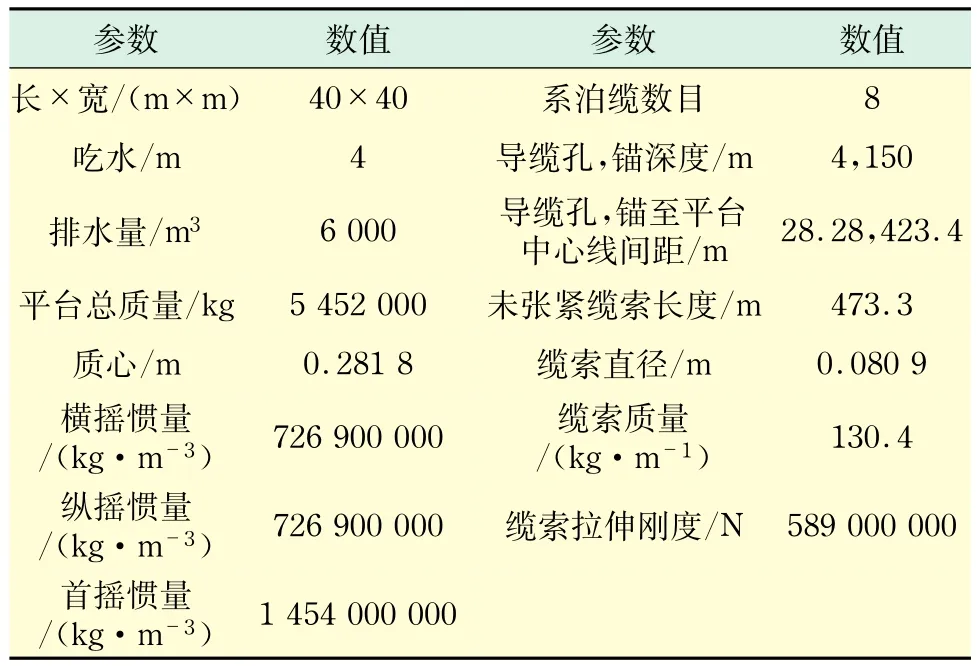
表1 ITI Energy Barge平台参数Tab.1 Parameters of ITI Energe Barge
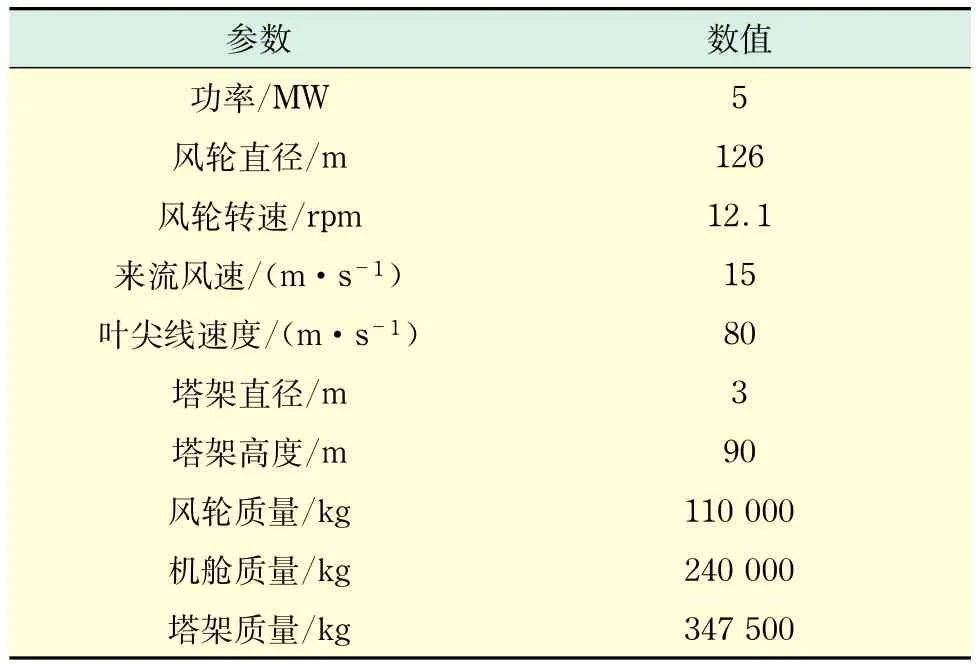
表2 风力机参数Tab.2 Parameters of wind turbine
2.2 响应自由度和波浪谱
波浪载荷作用下Barge平台在纵荡、垂荡、横荡、横摇、纵摇、首摇6个自由度上的运动强弱可由幅值响应算子RAO(response amplitude operator)描述.RAO是由波浪激励到Barge平台运动的传递函数,为Barge平台运动谱与波浪谱之比,表征单位波幅下Barge平台的特征响应.
随机波浪可认为是由若干个不同振幅、频率、初相位和传播方向的简单余弦波的叠加.一般把波浪作用下引起的平台的摇荡运动看成是具备各态历经性的平稳的随机过程,Barge平台对任意一个波浪的响应是该成分波浪波幅的线性函数,同时与其他成分作用下的响应独立无关.因此,利用Barge平台各自由度的运动RAO给出在每一个波浪频率下的平台响应并叠加求和,可得到在随机波浪作用下的Barge平台运动方程.故可用Barge平台RAO来反映在外界环境载荷激励下平台在6个自由度上的运动情况,进而反映平台的稳定性与否.

图1 风力机整机模型Fig.1 Whole machine model of the wind turbine
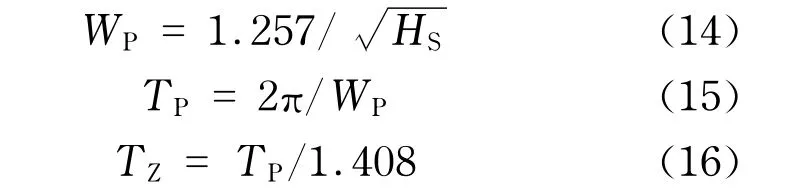
式中,HS为有义波高.
2.3 计算工况与处理步骤
采用有限元软件ANSYS中的水动力模块AQWA进行网格划分和数值计算,计算总时长共500 s,时间步长0.01 s.分析沿x轴、y轴和z轴的平动(即纵荡、横荡、垂荡)和绕x轴、y轴和z轴的转动(即横摇、纵摇、首摇)的各种响应,漂浮式平台在六自由度上的运动如图2所示.
具体环境条件设定如下:
波浪谱是随机海浪的一个重要统计性质,它不仅包含着波浪的二阶信息,同时还给出波浪组成波能量相对于频率和方向的分布情况.常用的波浪谱形有P-M谱、JONSWAP谱和文圣常谱等.P-M谱是根据大量的实测数据于1964年提出的波浪谱,适用于描述充分发展的波浪.同时,P-M谱是经验谱,依据资料比较充分,分析方法合理,使用方便.故本文波浪谱选择P-M谱.波浪的特征参数谱峰频率WP、谱峰周期TP、跨零周期TZ的计算分别为:
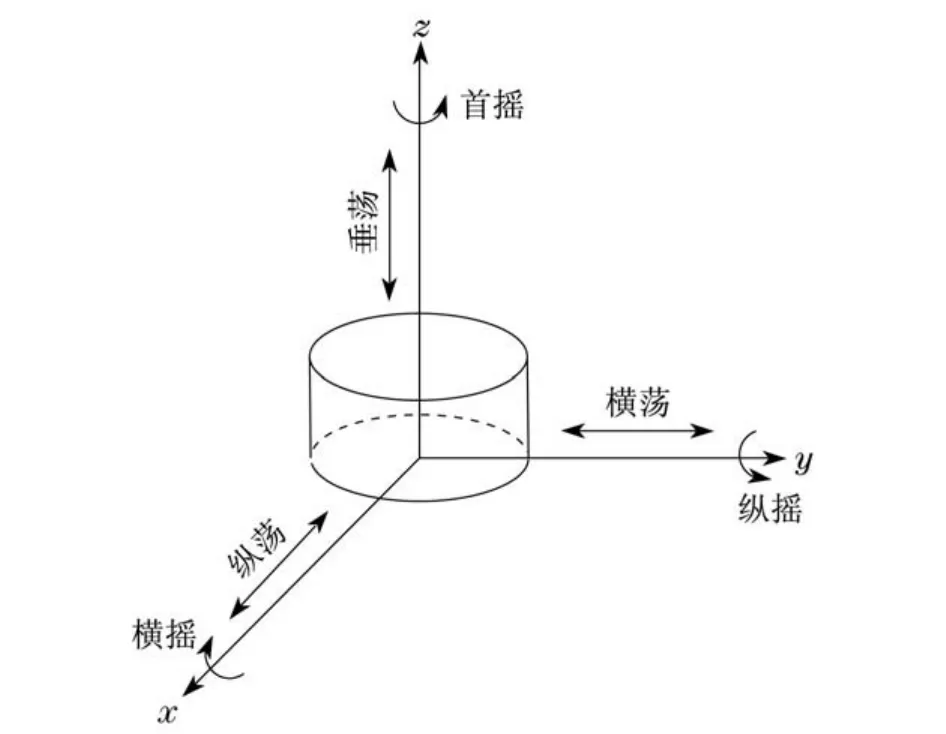
图2 平台六自由度运动Fig.2 Movements of the platform in six degrees of freedom
a.风浪流均垂直入射风力机风轮迎风面方向的最恶劣情况;
b.来流风速为15 m/s全域稳态风;
c.波浪谱为P-M谱,有义波高2.5 m,跨零周期为5.61 s;
d.海流速度由海平面至海底由2 m/s线性减至0.
3 结果与分析
3.1 时域特性分析
漂浮式风力机Barge平台最直观的响应是在外界环境载荷作用下的位置变化,即平动位移、转动偏转角.图3和图4分别为风浪流载荷联合作用下时域平动RAO和转动RAO,纵坐标表征单位波幅作用下的位移和偏转角.由图3和图4可知,在风浪流载荷作用下,Barge平台在纵荡、横荡、垂荡、横摇、纵摇和首摇6个自由度上均作不规则往复运动,且都存在峰值时间和峰值频率.平台平动,横荡、垂荡方向运动幅度远远小于纵荡方向,其幅度相差约2个数量级;平台转动,横摇、纵摇和首摇位于相同数量级,但首摇幅度稍稍大于横摇和纵摇.

图3 时域平动RAOFig.3 Time domain RAO of distance
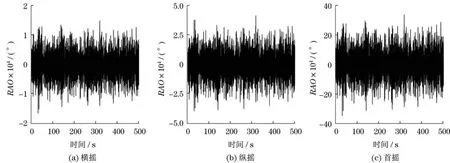
图4 时域转动RAOFig.4 Time domain RAO of rotation
3.2 频域特性分析
图5和图6为Barge平台的RAO随波浪频率的变化,其中纵坐标为单位波幅作用下的RAO.从图5和图6可知,在波浪作用下,平台在六自由度方向上运动响应均随频率变化,且存在峰值频率.平动的纵荡、垂荡方向的响应数量级大致相同,但峰值频率差异较大,两者在高频时(纵荡ω>1.0 rad/s;垂荡ω>1.25 rad/s)响应趋于零,响应主要集中在低频区;相比纵荡和垂荡,横荡方向响应较小,数量级远小于前两者.转动的横摇、首摇方向响应数量级大致相同,且都存在峰值频率,响应主要集中于0.5~2.5 rad/s,在低频(ω<0.5 rad/s)和高频(ω>2.5 rad/s)运动响应趋于零;而纵摇方向响应数量级大于横摇和首摇方向,响应主要集中在0~1.5 rad/s,存在峰值频率,在高频(ω>1.5 rad/s)运动响应趋于零.
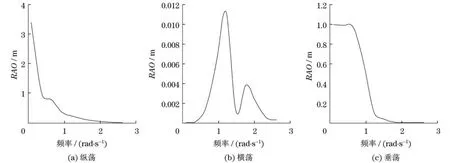
图5 频域平动RAOFig.5 Frequency domain RAO of distance
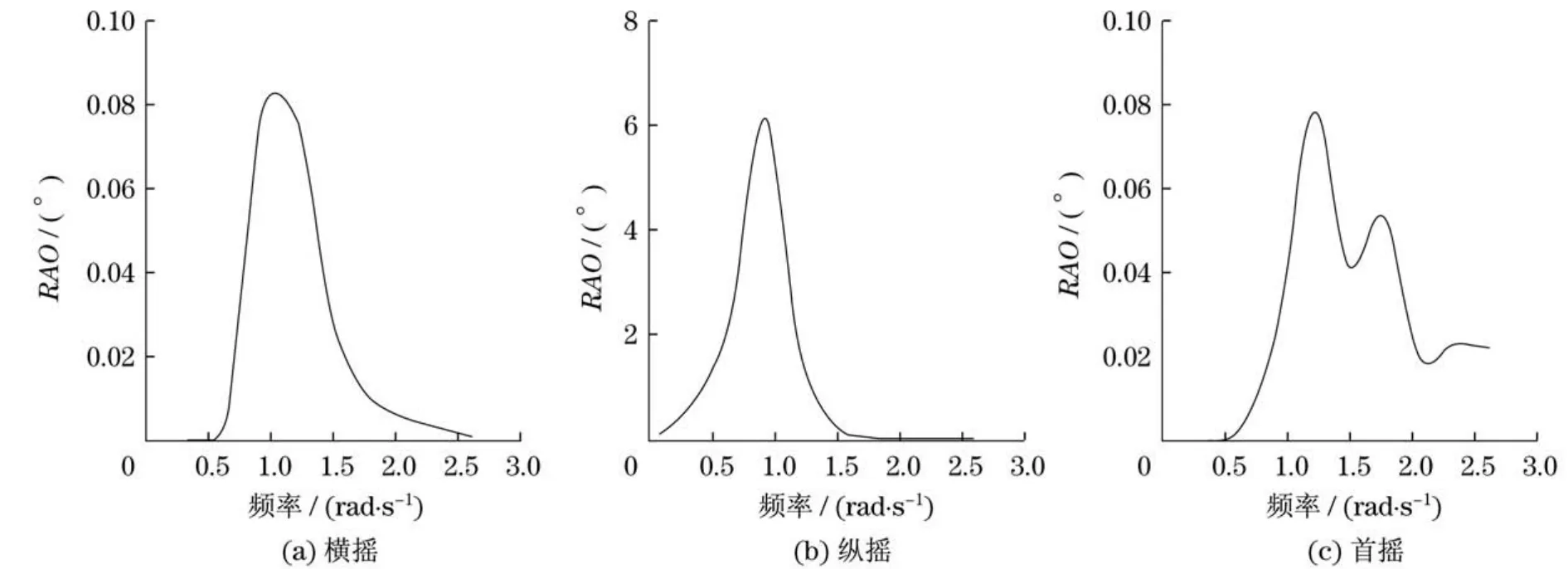
图6 频域转动RAOFig.6 Frequency domain RAO of rotation
图7和图8分别为平台平动和转动方向上各自由度F-K力随波浪频率的变化.由图7可知,平台在纵荡、横荡、垂荡3个方向上F-K力均存在峰值和峰值频率;平台在纵荡、垂荡方向上所受F-K力数量级远大于横荡方向,与纵荡、垂荡方向相比,横荡方向力可忽略不计;垂荡方向上F-K力在低频(0~1.2 rad/s)区受频率影响比较明显,当ω>1.2 rad/s时,垂荡方向F-K力逐渐减小并趋于0.由图8可知,平台在横摇、纵摇、首摇3个方向上的F-K力矩均存在峰值和峰值频率,在ω<1.5 rad/s频率范围内,纵摇F-K力矩大于横摇、首摇方向;当ω>1.5 rad/s时,纵摇方向F-K力矩趋于零;首摇方向F-K力矩受波浪频率增加逐渐增大,局部有减小趋势.
图9和图10(见下页)为平台平动和转动方向各自由度绕射力随波浪频率的变化.从图9可知,平台在平动三自由度方向上所受的绕射力均存在峰值和峰值频率,纵荡、横荡方向绕射力随波浪频率变化响应趋势大致相同,均在1.2 rad/s和1.8 rad/s附近时得到极大值,但横荡方向响应数量级小于纵荡方向;垂荡方向绕射力数量级最大,并在0.8 rad/s附近取得最大值;垂荡方向绕射力集中在低频波段(ω<1.5 rad/s),而当ω>1.5 rad/s时,绕射力逐渐减小并趋于零.由图10可知,平台在转动三自由度方向上所受的绕射力矩均存在峰值和峰值频率.横摇、首摇方向力矩数量级大致接近,均在1.2 rad/s和2 rad/s附近取得极大值;纵摇方向绕射力矩数量级远大于横摇、首摇方向力矩,并在1.2 rad/s附近取得最大值;与纵摇方向绕射力矩相比,横摇、首摇方向绕射力矩可忽略.

图7 F-K力Fig.7 Force of F-K

图8 F-K力矩Fig.8 Moment of F-K
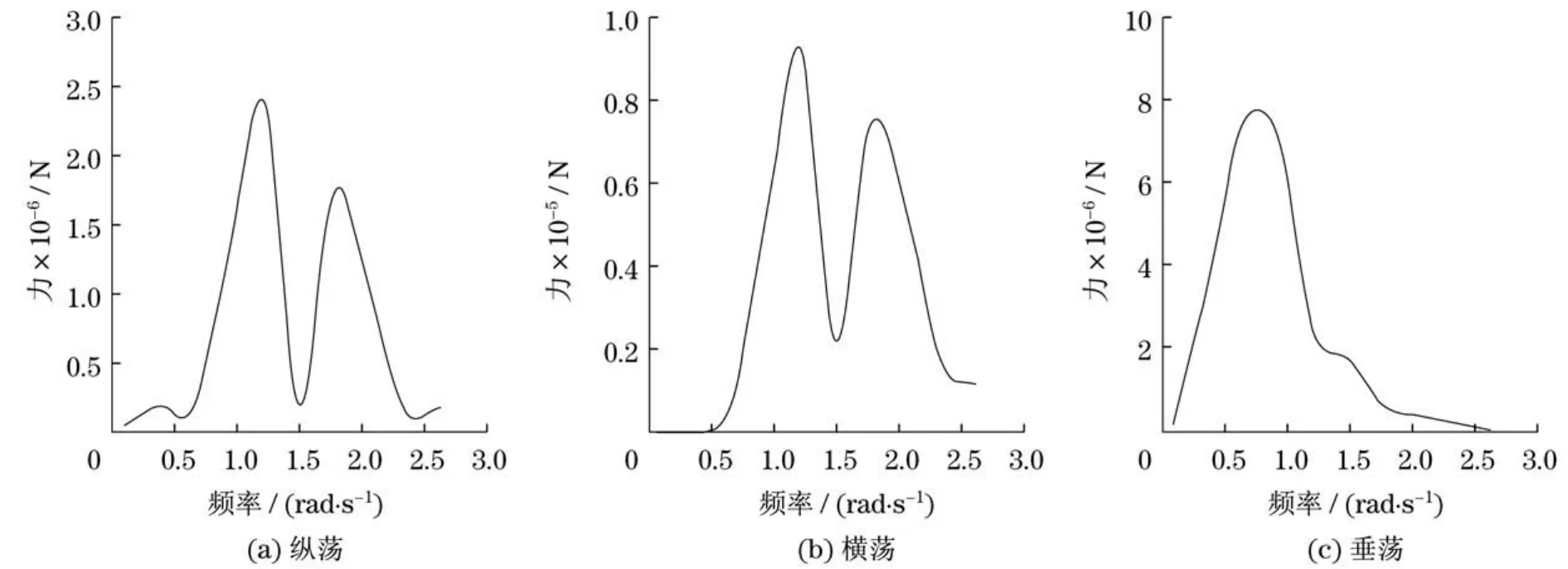
图9 绕射力Fig.9 Force of diffraction

图10 绕射力矩Fig.10 Moment of diffraction
4 结 论
利用三维建模软件Catia建立基于ITI Energy Barge平台NREL 5MW漂浮式风力机模型,探究其在风浪流载荷联合作用下的时域动态响应和波浪载荷频域特性,具体结论如下:
a.漂浮式风力机Barge平台在频域变化范围内,运动响应平动主要在纵荡和垂荡方向,且都是集中在低频(ω<1.2 rad/s)部分,平台转动运动响应主要是纵摇方向,横摇、首摇相对于纵摇可忽略不计.由此可见,优化漂浮式平台的纵荡、垂荡和纵摇方向的运动将对漂浮式平台乃至于整个风力机系统的稳定性有着重要意义.
b.F-K力和绕射力在垂荡和纵摇方向上的数量级远大于其他方向,F-K力在垂荡和纵摇方向集中在0.5~1.5 rad/s之间;绕射力在垂荡方向主要集中在0.08~1.5 rad/s之间,在纵摇方向主要集中在0.5~2 rad/s之间.F-K力和绕射力对漂浮式海上风力机作用力十分明显.
c.平台各自由度上的运动在低频波浪作用下容易出现较大响应.
[1] 张亮,吴海涛,荆丰梅,等.海上漂浮式风力机研究进展及发展趋势[J].海洋技术,2010,29(4):122-126.
[2] 黄维平,刘建军,赵战华.海上风电基础结构研究现状及发展趋势[J].海洋工程,2009,27(2):130-134.
[3] 高月文,李春,叶舟,等.海上风力机桩柱式结构动力响应分析[J].上海理工大学学报,2013,35(6): 591-595.
[4] 高坤.海上漂浮式风力机的概念设计与仿真研究[D].上海:上海理工大学,2010.
[5] 徐建源,祝贺.风波联合作用海上风力机动态特性分析[J].中国电机工程学报,2010,30(5):120-124.
[6] 张亮,邓慧静.浮式风机半潜平台稳性数值分析[J].应用科技,2011,38(10):13-17.
[7] Vijfhuizen W J M J.Design of a wind and wave power barge[D].UK:Glasgow Universities of Glasgow and Strathclyde,2006.
[8] Wayman E N.Coupled dynamics and economic analysis of floating wind turbine systems[D].USA: Massachusetts Institute of Technology,2004.
[9] Wayman E N,Sclavounos P D,Butterfield S,et al. Coupled dynamic modeling of floating wind turbine systems[C]//Offshore Technology Conference Houston.USA:Golden,2006:108-115.
[10] Sebastian T,Lackner M.Analysis of the induction and wake evolution of an offshore floating wind turbine [J].Energies,2012,5(4):968-1000.
[11] 唐友刚,沈国光,刘丽琴.海洋工程结构动力学[M].天津:天津大学出版社,2008.
[12] Jonkman J,Matha D.A quantitative comparison of the responses of three floating platforms[C]//European Offshore Wind 2009 Conference and Exhibition. Stockholm,2009:212-219.
(编辑:董 伟)
Per formance of Barge Platform for Floating Wind Turbines
DINGQinwei1, LIChun1,2, CHENGXin1, YEZhou1,2
(1.School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China; 2.Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering,Shanghai 200093,China)
The stability of platform structure is the most basic guarantee for safety operation of offshore wind turbines.A whole machine model was built based on the ITIenergy barge platform to research the time-domain dynamic response and frequency-domain performance under certain wind,wave and current conditions.Dynamic responses of the platform structure were analyzed under the time-varying conditions of structure amplitude and wave frequency.The contribution of F-K force and diffraction force to the structure with six degrees of freedom movement as well as the changing tendency of the wave force along with the change of frequency were analysed.The results show that the response amplitude operator(RAO)of platform and the wave force acting on platform are prone to get large under low frequency wave action.The structural responses in the heave,surge and pitch directions are obvious than those in the other three directions.
floating wind turbine;barge platform;dynamic response
TK 83
A
1007-6735(2015)05-0425-08
10.13255/j.cnki.jusst.2015.05.003
2014-08-03
国家自然科学基金资助项目(E51176129);教育部高等学校博士学科点专项科研基金资助项目(20123120110008);上海市教委科研创新重点项目(13ZZ120,13YZ066)
丁勤卫(1990-),男,硕士研究生.研究方向:风力发电.E-mail:m18301928952@163.com
李 春(1963-),男,教授.研究方向:流体力学、能源规划与风能利用.E-mail:lichunusst@163.com

