扩缩通道内流动和换热非线性特性的数值模拟
刘丽娜, 杨 茉, 王治云, 黄文和, 严祯荣, 陆廷安
(1.上海理工大学能源与动力工程学院,上海 200093;2.上海市特种设备监督检验技术研究院,上海 200062; 3.上海市浦东新区特种设备监督检验所,上海 200136)
扩缩通道内流动和换热非线性特性的数值模拟
刘丽娜1, 杨 茉1, 王治云1, 黄文和2, 严祯荣2, 陆廷安3
(1.上海理工大学能源与动力工程学院,上海 200093;2.上海市特种设备监督检验技术研究院,上海 200062; 3.上海市浦东新区特种设备监督检验所,上海 200136)
对扩缩通道内流动与换热进行了数值模拟并探讨了其中的非线性特性.通过对不同突扩比ER、不同长宽比AR及不同雷诺数Re下通道内流场和温度场进行分析,给出在一定工况下对称通道内流体的流动和换热会出现偏斜等非线性现象的情况.数值模拟结果表明,存在临界雷诺数Rec使流体流动和换热形态发生转变,当Re超过Rec时,流体流动和换热不仅有对称解,还有非对称解;当Re继续增大时,流体流动和换热出现振荡.通道的几何尺寸及后缩段(表现为ER及AR)都对Rec产生影响.分析结果表明,当Re超过临界雷诺数Rec时,同一截面处上下壁面的局部努塞尔数Nu也由对称向非对称转变,上下壁面出现最大局部Nu的位置也不同.
突扩或扩缩通道中的流动与换热在工业上有广泛的应用,同时也是理论研究的经典问题.对于突扩通道内的流动与换热,当几何和边界条件都对称时,一般认为其解也是对称的.因此,在进行理论研究时,通常取一半的区域进行研究.陶文铨院士所著《数值传热学》[1]中所给出的该问题的数值解就是取一半区域进行计算得到的.但实际上,由于这种流动和换热是非线性的,解不是唯一的,在对称边界条件下,除了存在对称解外,还可能存在非对称解.Durst等[2]用实验和数值模拟的方法分别研究了低雷诺数下流体流经二维和三维突扩通道时的流动特性,发现在低Re下流体流动关于通道轴对称,但随着Re增加,流动向某侧壁面偏斜.按照非线性动力学理论的观点,非线性方程的定态解会在特征参数达到临界值时发生静态分岔,因而出现非对称解.近年来,突扩通道中的流动和换热仍受到研究者们的关注.赵海燕等[3]对突扩管中流动问题取一半区域进行了数值模拟,给出了不同Re和不同ER情况下的流线图,分析了它们对突扩管流的影响;周再东等[4]也是取一半区域,利用FLUENT软件对突扩管道中不同Re,不同ER下油的流动形态进行了数值模拟.显然,仅仅给出突扩通道中流动和换热的对称解是不够的,研究其非线性特性及其给出非对称解,无论从应用的角度还是理论研究的角度,都十分有价值.
近些年来,越来越多的研究者开始关注流动与换热中的非线性问题.人们对非线性问题的研究常常能够揭示一些非常奇妙的现象,使人类对自然界的理解更加深刻.Panagiotis[5]采用幂函数和高斯模型分别研究了广义牛顿流体流经整个突扩通道时,流体由对称向不对称流动的转变,给出了转变的Rec值.Thiruvengadam等[6]采用SIMPLEC算法、二阶上风差分格式研究了三维突扩通道中垂直向上流动中浮升力和通道尺度对混合对流解的分岔的影响.Kitoh等[7]采用QUICK差分格式利用数值模拟研究了水平突扩通道尺度效应对解的分岔现象的影响.耿丽萍等[8]采用大涡模拟方法数值研究了喷嘴内部自激励旋进射流的流动,其数值模拟结果显示,即使射流进入对称的圆筒中,突然膨胀后的流动也是不稳定的,会产生偏斜和切向速度.Mi等[9]研究了圆柱喷嘴中流体射流,结果表明,旋进射流喷嘴的结构参数必须在一定的范围内方可产生旋进运动模式占优的射流,主要的参数是膨胀比和膨胀腔的长径比,旋进射流的产生还与喷嘴入口和出口的结构、形状有一定关系.Zhang等[10]用数值方法研究了圆筒内开缝圆筒的自然对流特性及其非线性,结果表明,当Ra<4×105时,该系统处于稳定对称状态;当Ra>6×105时,得到非对称周期解;Ra进一步增加,振荡流经历几个分支,最终发展到混沌状态.申春赟等[11]采用SIMPLE方法对圆内开缝圆在不同开缝方向时的自然对流换热进行了数值模拟,结果表明,水平开缝的圆内开缝圆自然对流换热,随着Ra的增加,能够获得稳定解、周期性振荡解及非周期振荡解,最终为混沌.金硕宏等[12]对矩形腔内冷热壁面位于侧壁不同相对位置时的自然对流换热问题进行了数值模拟.
对于突扩通道内单纯流动的非线性现象已有文献报道,但同时考虑换热的研究成果较少.而且作者通过数值模拟注意到,突扩后再收缩的扩缩通道与单纯的突扩通道相比,其中的流动和换热的非线性特性会发生变化.这种扩缩通道中流动与换热的非线性特性,目前还没有研究成果公开报道.本文采用具有QUICK差分格式的SIMPLE算法和非稳态模型,以整个通道为计算区域,对扩缩通道中的流动和换热进行了数值模拟,分析了不同Re和通道几何尺寸变化时扩缩通道中流动和换热特性及其非线性特性.本文的研究表明,扩缩通道中的流动和换热存在对称解、非对称解及振荡解.随着Re,ER及AR等影响因素的变化,可能获得不同类型的解.
1 计算模型和数学描述
1.1 物理模型
该问题的物理模型如图1所示(见下页),其中上下两块板在垂直纸面方向为无限大平板,壁面温度为TW.通道的几何和物理条件关于水平中心轴线完全对称,流体进口速度均匀为U0,温度为T0.假设问题为二维、不可压缩流体、常物性,忽略粘性耗散,不考虑重力作用,出口符合局部单向化假设.
图中,h1为流体进口通道的高度;h2为流体出口通道的高度;H为突扩后通道高度;L1为流体进口段AB长度;L3为流体出口段CD长度;L2为通道突扩段长度.定义突扩比ER=H/h1,长宽比AR=L2/ h1,其中h1=h2.考虑到充分发展的入口段效应,取L1=10 h1,L3=L1,取工质Pr=4.34.
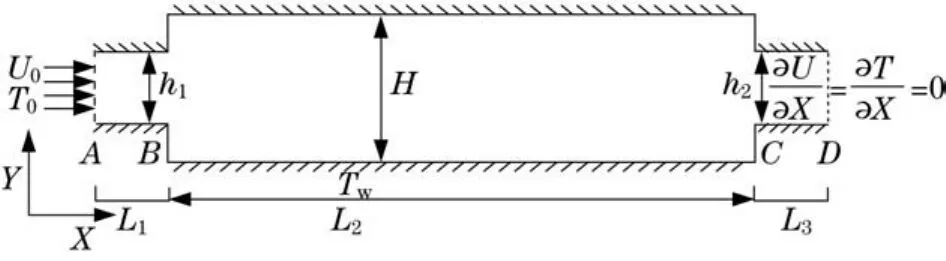
图1 物理模型Fig.1 Physical model
1.2 数学模型和边界条件
定义下列无量纲参数:

式中,x和y为坐标变量;τ为时间变量;u,v分别为x和y方向的速度分量;T,p分别为温度和压力;a,υ,ρ分别为热扩散系数、运动粘度、密度.图1所示的扩缩通道内强制流动和换热问题在直角坐标系下的无量纲数学描述为

式中,Θm为平均无量纲温度.
1.3 数值方法及考核
本文采用有限容积法[1],交错网格进行差分离散,差分方案采用QUICK格式,速度和压力耦合用SIMPLE算法.为了检查网格对结果的影响,本文采用202×152,362×152,462×152网格分别进行数值模拟.202×152,362×152网格监测点速度值模拟结果与462×152的结果相比,差别分别为3.1%和0.56%,最终数值计算采用的网格是362×152,时间步长取0.005.
2 数值模拟结果分析
本文根据数值模拟结果,分析了Re,ER,AR对扩缩通道内强制对流的影响,通过分别改变通道的Re,ER,AR来研究流体的流动和换热的特性,以及流动和换热从对称到不对称的转变过程.
2.1 不同雷诺数时的流场
图2示出了Re为50,300,1 000时通道内流体的流线图,其中ER=2,AR=20.由图2可知,通道ER和AR一定时,随着Re的增大,流体的流动状态会发生改变.在低Re时,例如Re=50,流体的流动呈现完全的对称状态;当Re高于临界雷诺数Rec时,流体的流动开始出现不对称的现象,流动会偏离通道的中心线向固体壁面发生偏斜,例如Re=300时;且随着Re的增加,流体流动的偏斜程度增加,流体流动变得越来越紊乱,流动出现振荡.流体流经突扩段时,在突扩处都会形成回流区,回流区的长度与Re有关,当Re低于Rec时,上下通道的回流区长度一样;当Re大于Rec时,通道内流体在上壁面的回流区长度大于下壁面的,且随着Re的继续增加,上下壁面回流区的长度差值也越来越大.
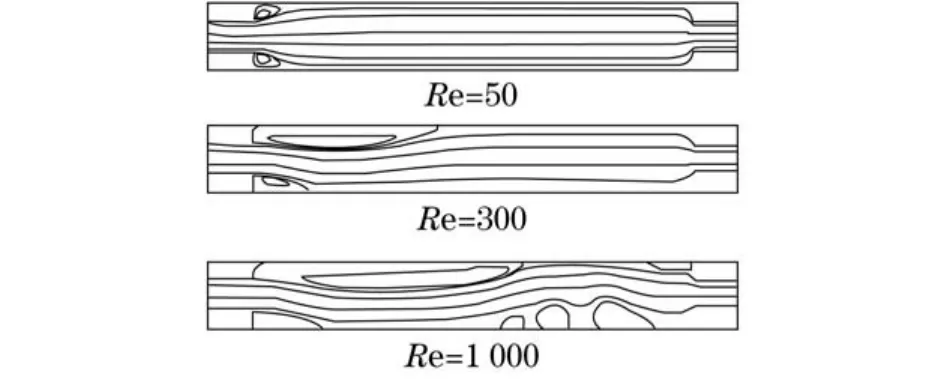
图2 不同Re下流线图(E R=2,A R=20)Fig.2 Streamline diagram under different Re (E R=2,A R=20)
从数值研究结果可得出,不同Re时,该数学模型中监测点的速度随时间t变化的情况是不同的.当Re很小时,监测点的速度值不随时间变化;当Re增大超过某一临界值时,监测点的速度随着时间振荡;当Re再增大时,监测点的速度随着时间振荡表现为混沌状态.从图3可以看出,当Re=600时,监测点的速度随着时间的变化一直处于振荡状态,不会随着时间的变化而稳定在某一特定值.
2.2 不同Re下局部努赛尔数Nu
流体流经该突扩后突缩的通道时会与壁面发生换热,为了研究流体与壁面的换热,本文计算了通道内L1段上下壁面的局部Nu值.图4显示了ER= 2,AR=20,Re=50,100,200,300时,流体流经该扩缩通道时上下壁面的局部Nu值.图4中的x是水平方向距突扩截面的长度,h为进口段高度.Nu为负时,表示下壁面的局部Nu值,Nu为正时,表示上壁面的局部Nu值.从图4可以看出,Re不同时,上下板与流体的换热由对称到不对称转变,Re越大,上下板Nu值的差异越大.
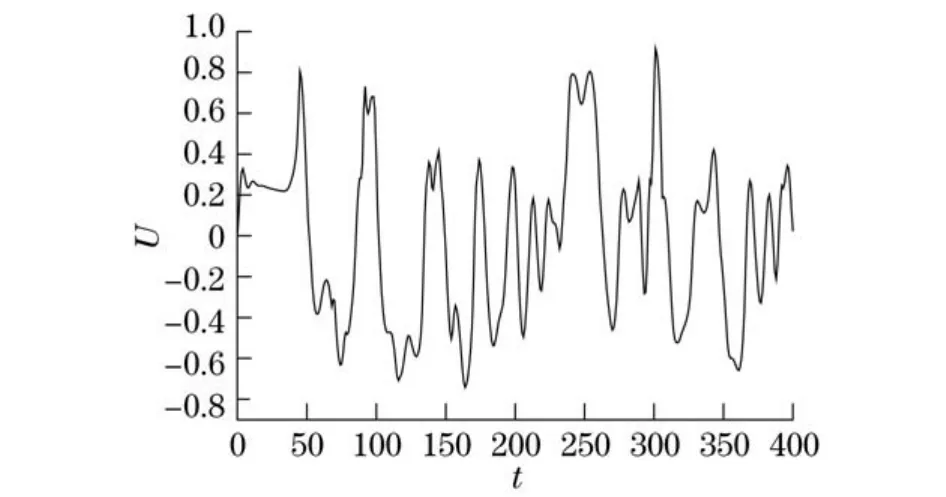
图3 监测点速度随时间的变化(A R=20,E R=3,Re=600)Fig.3 Monitoring velocity at different times (A R=20,E R=3,Re=600)

图4 不同Re时上下壁面局部Nu值(E R=2,A R=20)Fig.4 Local Nu number under different Re (E R=2,A R=20)
2.3 不同E R下局部努赛尔数Nu
图5显示了AR=20,Re=100时,不同ER下上,下壁面局部Nu值.由图5可知,不同ER下,上下板的局部Nu值不同.本模拟中,ER=1.5时,上下板的局部Nu值差异不大,关于中心轴对称; ER=3时,上下板的局部Nu值呈现完全的不对称.
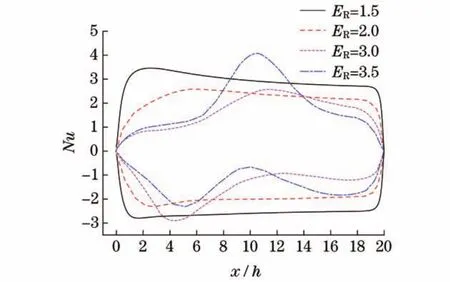
图5 不同E R下上下壁面Nu值(A R=20,Re=100)Fig.5 Nu number under different expansion ratio (A R=20,Re=100)
2.4 后缩段影响
从前文已知后缩段对通道内流体流动的影响,在一定AR内,后缩段的存在,对流体流动和换热的影响较大,超过一定AR时,后缩段的存在对通道内流体的流动和换热基本没影响.
图6显示了Re为100时,有后缩段以及无后缩段的通道内流体的流线图.如图6所示,当Re= 100时,流体流经扩缩通道和突扩通道时流体的流动状态完全相同,这时,后缩段对通道内流体的流动和换热不产生影响.
图7(见下页)显示Re=100,ER=3时,不同AR下流体与通道上下壁面换热的局部Nu值.由图7(a)可知,AR=5时,上下壁面的Nu值大小基本保持一致;由图7(b)可知,AR=10时,上下壁面Nu值的大小出现较大的差异;由图7(c)可知,AR=20时,上下壁面的最大局部Nu值的位置都出现在靠近突扩截面的前段,且下壁面最大局部Nu值出现的位置相对于上壁面偏后;由图7(d)可知,AR=40时,上下壁面的局部Nu值大小又开始基本保持一致,呈现对称状态.

图6 不同通道内流体流线图(Re=100,E R=3)Fig.6 Streamline chart in different channel (Re=100,E R=3)
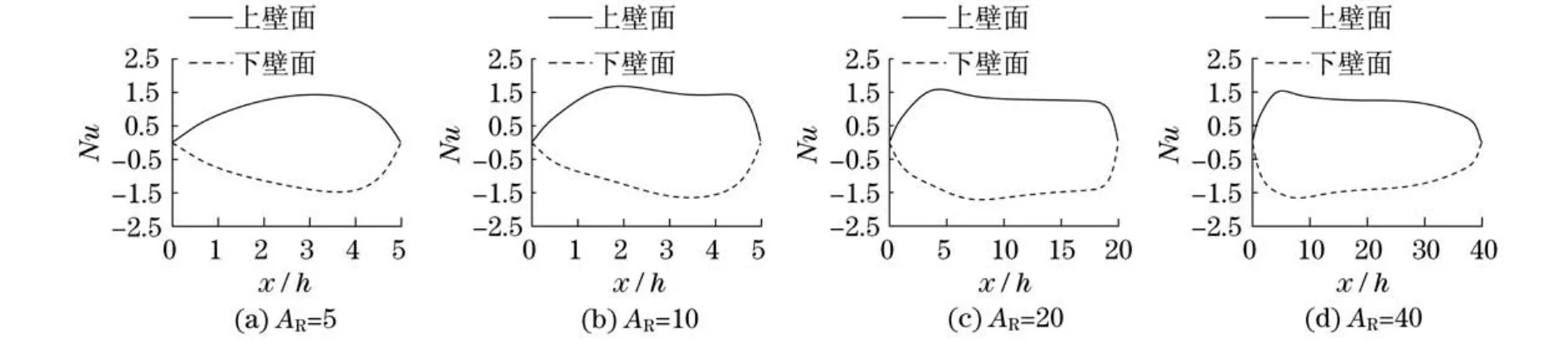
图7 不同长宽比时上下壁面的局部Nu值(Re=100,E R=3)Fig.7 Local Nu number under different aspect ratio(Re=100,E R=3)
3 结 论
a.当Re改变时,能够得到问题的对称解、非对称解和振荡解.Re小于临界雷诺数Rec时,解为唯一对称解;Re大于临界雷诺数Rec时出现非对称解.Re进一步增大,解随时间振荡.
b.在本文给定的几何和物理条件下,ER=4时,Rec=12,即Re<12时,流动和换热呈现对称状态;当Re≥12时,流动和换热呈现不对称的偏斜状态;Re继续增大到Re≥500时,流动和换热开始振荡.
c.通道的后缩段对临界雷诺数Rec的大小有影响.通道的突扩比ER越大,Rec越小;而AR对Rec的影响就不是单调的.在低Re时,AR较小时(AR=5),流动和换热是对称的;增大AR时(AR= 10),流动和换热不对称;继续增大AR(AR=30),流动和换热又呈现出对称状态.
[1] 陶文铨.数值传热学[M].2版.西安:西安交通大学出版社,2004.
[2] Durst F,Melling A,Whitelaw J H.Low Reynolds number flow over a plane symmetric sudden expansion [J].Fluid Mech,1974,64(1):111-128.
[3] 赵海燕,贾雪松,杨士梅,等.突扩管分离流体的数值模拟[J].科学技术与工程,2009,9(17):5238-5240.
[4] 周再东,魏长柱,孙明艳,等.突扩管流动形态的数值模拟[J].科学技术与工程,2012,12(30):7983-7985.
[5] Panagiotis N.Transition to asymmetry of generalised Newtonian fluid flows through a symmetric sudden expansion[J].Journal of Non-Newtonian Fluid Mechanics,2006,133(2):132-140.
[6] Thiruvengadam M,Armaly B F,Drallmeier JA.Threedimensional mixed convection in plane symmetricsudden expansion:bifurcated flow regime[J].ASME Journal of Heat Transfer,2007,129(7):819-826.
[7] Kitoh A,Sugawara K,Yoshikawa H,et al.Expansion ratio effects on three-dimensional separated flow and heat transfer around backward-facing steps[J].ASME Journal of Heat Transfer,2007,129(9):1141-1155.
[8] 耿丽萍,周静伟,陶容.基于柯恩达效应的自激旋进射流流动特性研究[J].中国机械工程,2009,10(10): 1217-1221.
[9] Mi J,Nathan G J,Wong C Y.The influence of inlet flow condition on the frequency of self-excited jet precession[J].Journal of Fluids and Structures,2006, 22(1):129-133.
[10] Zhang K,Yang M,Zhang Y.Numerical analysis of natural convection in a cylindrical envelope with an internal concentric cylinder with slots[J].Numerical Heat Transfer,Part A:Applications,2011,59(10): 739-754.
[11] 申春赟,杨茉,王津,等.圆内开缝圆不同开缝方向自然对流换热[J].上海理工大学学报,2013,35(5): 425-429.
[12] 金硕宏,刘建国,李凌,等.热壁面位置对矩形腔内自然对流影响的数值分析[J].上海理工大学学报, 2014,36(6):527-531.
(编辑:丁红艺)
Nonlinear Flow and Heat Transfer Phenomena in a Channel with Sudden Expansion Followed by Sudden Contraction
LIULina1, YANGMo1, WANGZhiyun1, HUANGWenhe2, YANZhenrong2, LUTingan3
(1.School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China; 2.Special Equipment Supervision and Inspection of Shanghai Institute of Technology,Shanghai 200062,China; 3.Shanghai Pudong New Area of Special Equipment Supervision and Inspection,Shanghai 200136,China)
The Newtonian fluid flow in a rectangular channel with sudden expansion followed by sudden contraction was simulated numerically for the whole flow region.The nonlinear characteristics and temperature field were investigated with various Reynolds numbers and geometrical dimensions.The results show that the temperature field will evolve from symmetric state to asymmetric state with the increase of Re.When Re<Rec(critical Reynolds number),the symmetric state is stable.However,when Re≥Rec,the flow loses stability and develops from symmetric state to asymmetric state via a symmetry-breaking bifurcation.The expansion ratio and aspect ratio can affect the value of the critical Reynolds number.The analysis results show that when the Re number is greater than the critical Re,Nu number will change significantly,and then affect the heat transfer of the pipeline.
sudden expansion followed by sudden contraction channel;numerical simulation;non-linearity;heat transfer
突扩突缩通道;数值模拟;非线性;换热
TK 124
A
1007-6735(2015)05-0440-05
10.13255/j.cnki.jusst.2015.05.005
2014-10-26
国家自然科学基金资助项目(51476103,51306121);上海市教委科研创新资助项目(14ZZ134);上海市质量技术监督局公益科研项目(201212,201241)
刘丽娜(1989-),女,硕士研究生.研究方向:传热及数值技术的研究.E-mail:1013546508@qq.com
杨 茉(1958-),男,教授.研究方向:流动和传热的数值模拟.E-mail:yangm@usst.edu.cn

