电力系统低频振荡监测的Duffing振子可停振动系统法

赵 妍 李志民 李天云

（1.哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001 2.东北电力大学输变电技术学院 吉林 132012）

0 引言

我国互联电网规模和范围的成倍增长以及特高压电网的发展，提高了电网运行的可靠性和经济性的同时，也带来了新的安全隐患。近年来多次发生的低频振荡严重危及了电网的安全稳定运行，引起了工业界和学术界的广泛关注。目前研究的热点主要集中在低频振荡辨识、低频振荡产生的机理和抑制低频振荡三个方面[1-6]。值得注意的是，这三类问题的研究前提是需要监测是否发生了持续、稳定的低频振荡。这是因为，实测低频振荡信号往往表现为一个典型的非线性、非平稳随机过程，即信号的统计性的时变特性（包括时域和频域统计特性），而在动态电力系统分析中往往同时存在多个非线性振荡模式，各振荡模式间存在着或强或弱的非线性相互作用，衍生出新的振荡模式，具有一定的不确定性和不稳定性，使低频振荡的处理更加复杂。低频振荡信号时域的主要特点为振荡模式出现的时间不确定、持续的时间不确定以及振幅带有阻尼特性且随时间变化。因此，在进行低频振荡的参数辨识时，应确定是否发生了持续、稳定的低频振荡。电力系统在故障或异常运行时，可能随机出现短暂的“低频振荡”，这类振荡模式存在时间短、可以自动平息，是无需处理的“瞬变的低频振荡模式”。然而，现在认可度较高的电力系统振荡分析方法都是以发生了低频振荡为假设前提的，并不进行此判别，可能会将瞬变的低频振荡模式误判为稳定的低频振荡信号，缺乏真实性。

另外，当电网发生低频振荡时，正确判断振荡模式和模式的阻尼特性，对合理选择振荡抑制措施、快速抑制振荡具有重要意义。低频振荡产生的机理包括负阻尼理论、强迫功率振荡理论和非线性理论等。负阻尼理论认为，电力系统负阻尼低频振荡是系统受扰动后的自由振荡，振荡衰减与否由系统的阻尼特性决定，若系统不存在负阻尼，则不会发生增幅低频振荡[7,8]。强迫振荡理论指出，持续的周期性小扰动会引起电力系统强迫振荡，当扰动频率接近于系统固有频率时，会导致系统出现大幅度的功率振荡，这种振荡的表现形式类似于负阻尼低频振 荡[8,9]。虽然负阻尼振荡和强迫功率振荡具有非常相似的表现形式，但是由于具有不同的发生机理，采用的抑制措施也不相同。在调度运行中，对于负阻尼机理引起的振荡主要采用各种增强系统阻尼的措施，抑制强迫功率振荡的最直接有效的方法就是迅速找到并切除扰动源。因此，在振荡发生时能够根据振荡特征迅速判断振荡模式，对于快速抑制振荡、防止振荡扩散具有重要意义。文献[10]结合负阻尼振荡和强迫功率振荡不同振荡阶段的振荡波形特征和振荡模式分布统计特征，对电力系统低频振荡性质进行了分析和判断，但是难以满足实时监测的需求。

为了解决上述问题，本文将可停振动系统理论应用于电力系统低频振荡监测与分析中，提出了低频振荡监测的Duffing 振子的可停振动系统分析方法。Duffing 振子的可停振动系统在受到微小随机扰动时以概率1 渐近稳定，其对应的状态称为可停振动状态。该系统输入恒定幅值周期信号时，系统有周期解或拟周期解为不可停状态。这类系统对周期信号敏感,对随机微小扰动不敏感,利用可停振动状态的改变，可以进行周期未知微弱信号检测[11]。

本文将量测信号输入到Duffing 振子的可停振动系统中进行分析，根据可停振动系统相轨迹的状态改变，可以跟踪系统运行方式的变化，对电力系统低频振荡的全过程进行可视化的监测。为调度员提供可视化图像，来判断是否发生了低频振荡、振荡模式和模式的阻尼特性。为快速准确地告警、合理地选择振荡抑制措施和快速抑制振荡提供依据。

1 Duffing 振子的可停振动系统

1.1 可停振动系统检测理论

定义 设随机微分方程

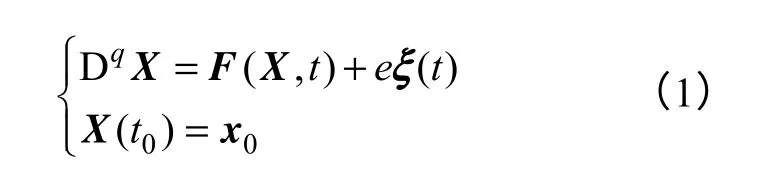
式中，X/F为二维矢量随机过程；q为微分方程的阶数，q∈ R；ξ(t)为系统输入的随机扰动；e为随 机扰动幅度；η0是其平凡解（F(η0,t)=0）。

②当系统（1）的输入为周期信号时，系统有周期或者是拟周期解。文献[11]中将其对应的状态称为可停状态，由定义可知：可停振动系统的可停振动状态变化对噪声不敏感，对周期信号敏感，因此通过系统的相平面轨迹可以在预先未知信号周期的情况下判断系统输入是否含有未知的周期信号。

1.2 Duffing 振子的可停振动系统

考虑Holmes 型Duffing 振子

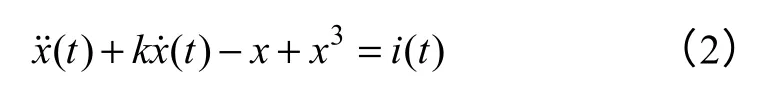
式中，i(t)为系统输入；k为阻尼系数。

将式（2）改写成一阶微分方程组的形式，并令系统输入为Guass 白噪声

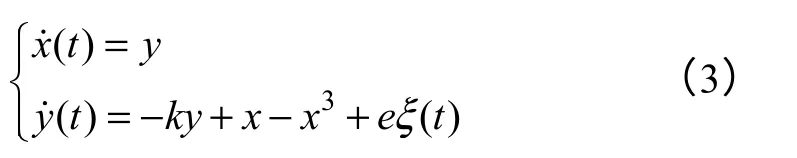
设k、e都为ε阶无穷小量[12,13]，则式（3）所示系统的Hamilton函数为

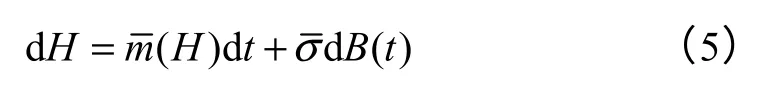
其中B(t)是标准的Winner 过程

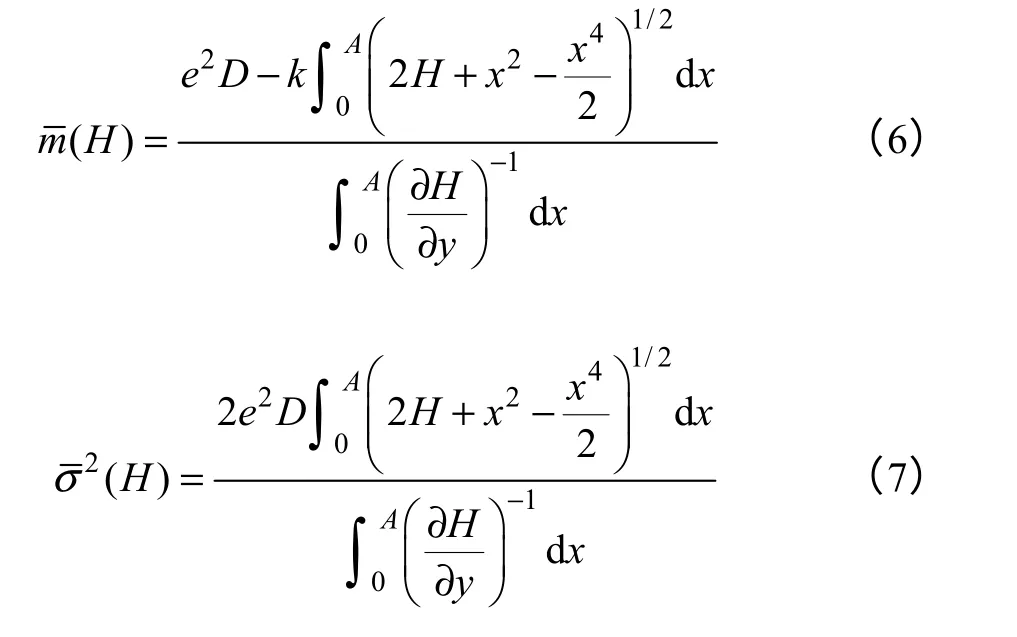
因此，在式（3）的平衡点（±1,0），方程（5）的Lyapunov 指数为

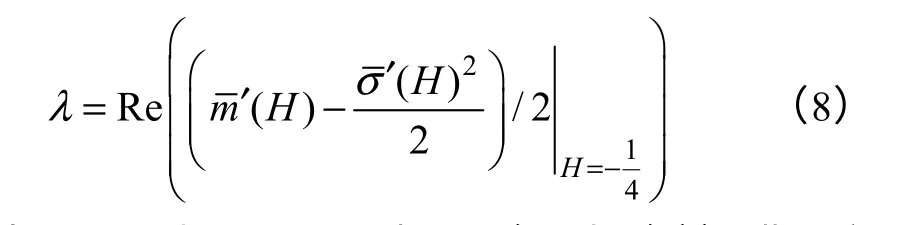
当k＞0时，Duffing 振子（见式（2））满足定义中的条件①[12]。又当k＞0时，系统输入为恒定幅值的周期信号时，Duffing 振子是耗散系统[13]。所以，当k＞0时，Duffing 振子是可停振动系统，因此可以利用Duffing 振子可停系统对未知周期、未知形式的微弱周期信号进行检测。

2 电力系统端部输出信号分析

电力系统端部输出信号即为模型（2）的i(t)，i(t)为Holmes 型Duffing 振子的激励，将i(t)输入到可停振动系统中进行相轨迹分析。i(t)的类型主要有恒定幅值的周期信号、白噪声信号、带噪的恒幅周期信号、衰减振荡信号、发散振荡信号及复合仿真信号。

2.1 第一类测试信号——周期、白噪声和带噪的周期信号

i(t)为恒定幅值的周期信号（0.1 cost）、白噪声为噪声强度）和带白噪声的周期信号（信噪比为3.01dB、−9.03dB），相轨迹如图1～图3所示，阻尼系数k=0.5。

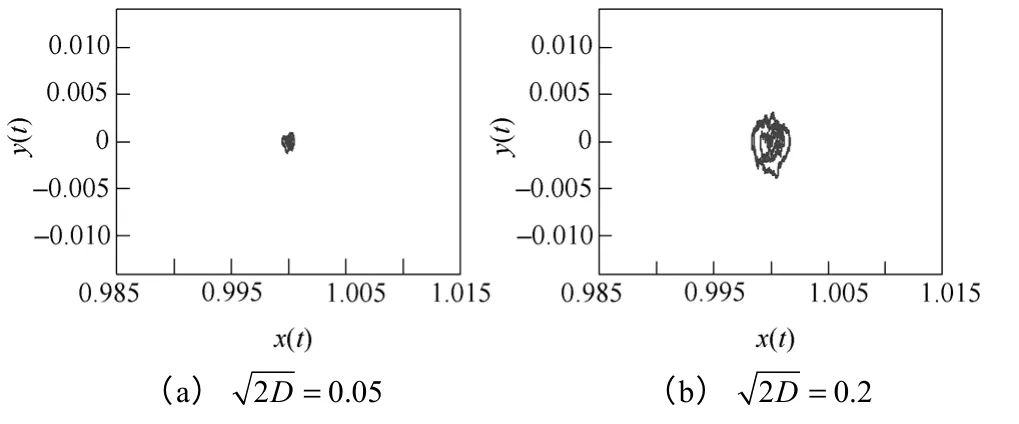
图1 i(t)为白噪声的相轨迹Fig.1 Phase trajectory of input white noise signal

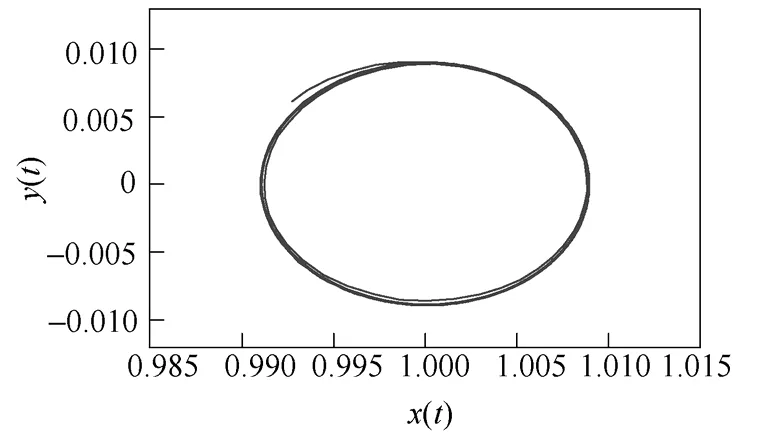
图2 i(t)为周期信号的相轨迹Fig.2 Phase trajectory of input periodic signal

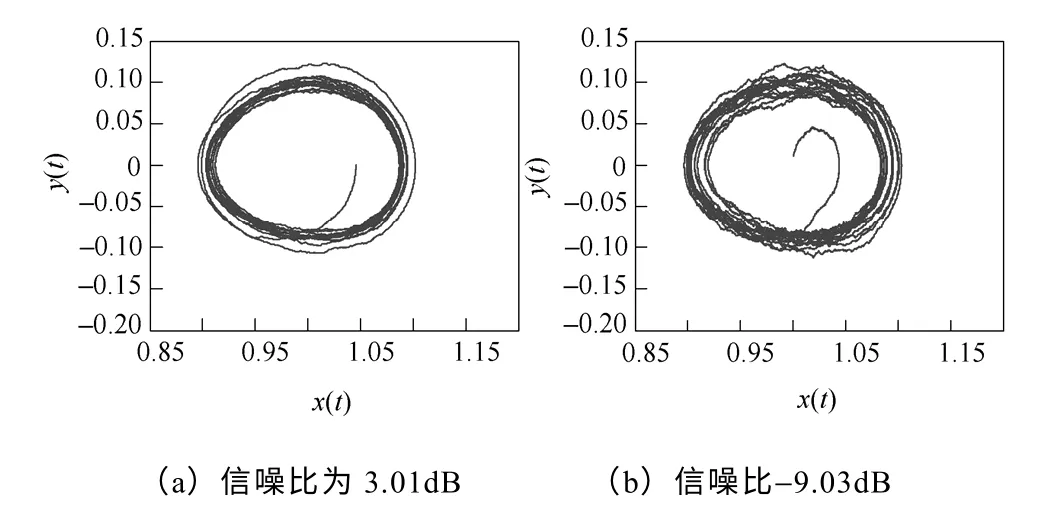
图3 i(t)为带噪周期信号的相轨迹Fig.3 Phase trajectory of input periodic signal with white noise

当i(t)中仅含有白噪声时，相轨迹聚焦为一点，系统处于可停振动状态；当i(t)中含有恒定幅值周期信号时，相轨迹为封闭圆环，表明系统立即从可停振动状态变化为小尺度周期状态。增加或者减小周期分量的幅值，幅值不同，相轨迹的封闭圆环数量也不同，但均为小尺度周期状态。注意小周期状态时，输入周期分量的幅值不应超过0.36。

比较图2和图3，只要i(t)中含有周期信号不论是否含有噪声，噪声强弱都为小尺度周期状态。噪声附加在封闭环上，以周期信号作为骨架，含噪后信号相图的拓扑结构不变。根据文献[11]噪声为Gauss 白噪声时，检测门限可达到−66dB，达到了极低的检测门限，该方法对噪声具有免疫性。

综上，可停振动状态的改变对周期策动力敏感，对零均值随机微小扰动不敏感。这就从仿真上也验证了系统（2）是可停振动状态系统，可以用于未知周期信号的检测。

2.2 第二类测试信号——衰减、发散振荡信号

i(t)为衰减振荡信号0.1e−0.1tcost、发散振荡信号0.1e0.1tcost，初值均为（1，0），相轨迹如图4和图5所示。

由图4和图5可知，i(t)为衰减振荡信号时，图形以初值螺旋收缩，将从减幅的小周期状态过渡到可停状态；i(t)为发散振荡信号时，图形以初值螺旋 发散，从增幅的小周期状态进入多周期状态。

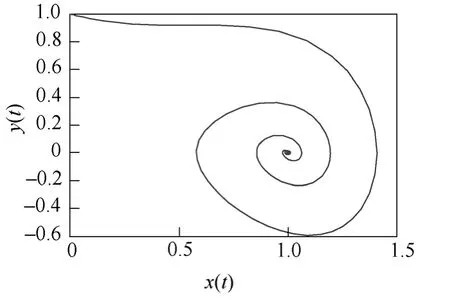
图4 i(t)为衰减振荡信号的相轨迹Fig.4 Phase trajectory of input damped oscillation signal

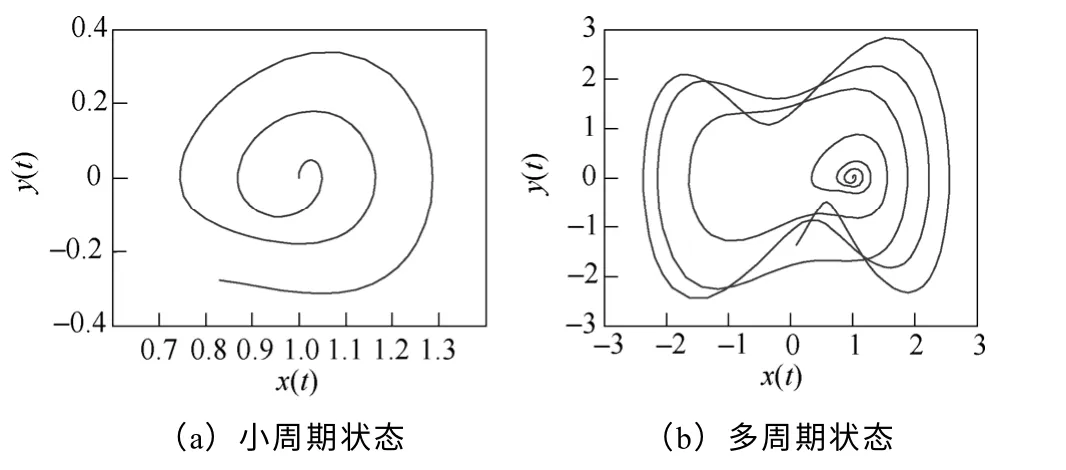
图5 i(t)为发散振荡信号的相轨迹Fig.5 Phase trajectory of input divergent oscillation signal

2.3 第三类测试信号——复合信号

2.3.1 复合测试信号1

构造一个含有噪声的复合测试信号模拟弱阻尼振荡，如图6所示。其表达式为

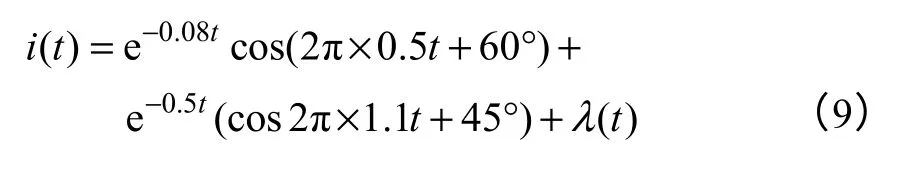
式中，λ(t)为白噪声，此信号包含了一个区域间振荡频率和一个区域内振荡频率，信噪比为9.17dB。为了使信号处于小尺度周期状态，将信号归一后乘以0.1 的系数，输入到可停振动系统中，改变仿真时间连续观察其相轨迹，其相轨迹如图7所示。此相轨迹以初值螺旋收缩，噪声附加在螺旋上，由小周期状态过渡到可停状态。可以判断信号中包含有衰减振荡信号，为弱阻尼振荡模式，噪声不影响相轨迹的拓扑结构。仿真时间为20s时，形成具有明显特征的轨迹图，通过对相轨迹的实时监测可以对低频振荡的过程进行可视化的监测，满足实时监测的快速性要求。

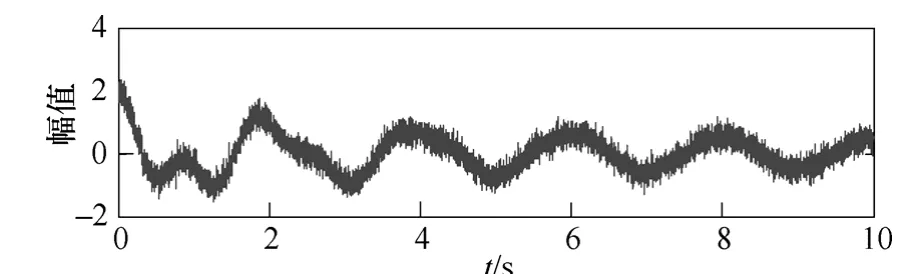
图6 含噪声的复合测试信号1Fig.6 The input composite test signal 1 with white noise

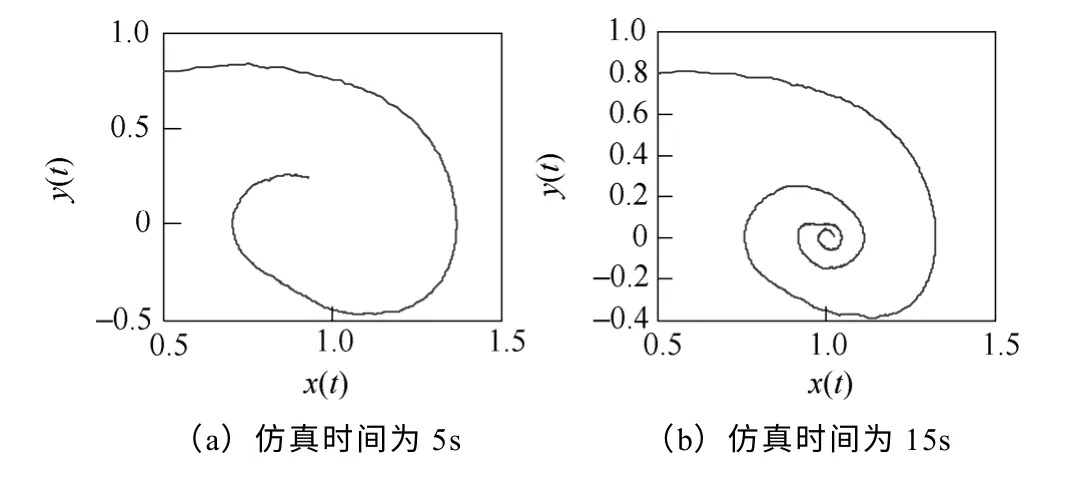
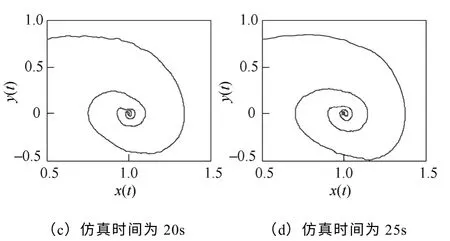
图7 含噪声的复合测试信号1 的相轨迹Fig.7 Phase trajectory of the input composite test signal 1

2.3.2 复合测试信号2

在文献[8]中指出，强迫功率振荡的特点是振荡波形瞬态阶段出现了明显的拍频，进入稳态阶段后其振荡幅值较为稳定，为等幅振荡的稳态振荡阶段。根据文献[8]构造另一个含有噪声的复合测试信号模拟强迫功率振荡；即

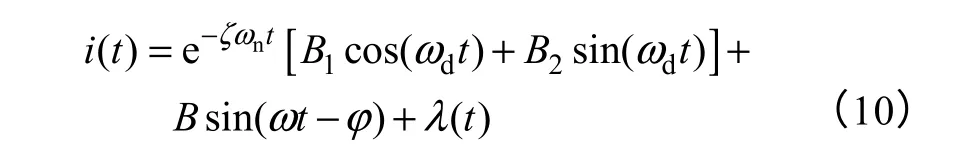
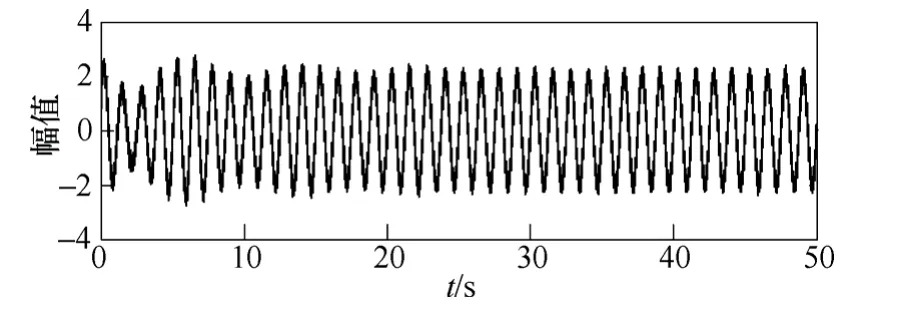
图8 含噪声的复合测试信号2Fig.8 The input composite test signal 2 with white noise

将该信号归一后乘以0.1 的系数输入到可停振动系统中，改变仿真时间连续地观察其相轨迹，信噪比为23.02dB，相轨迹如图9所示。

该相轨迹以初值螺旋收缩为封闭圆环（极限环），噪声附加在轨迹上，最终为小周期状态。可以判断信号中包含有衰减振荡信号和不衰减的振荡信号。仿真时间为25s时，形成具有明显特征的轨迹图。

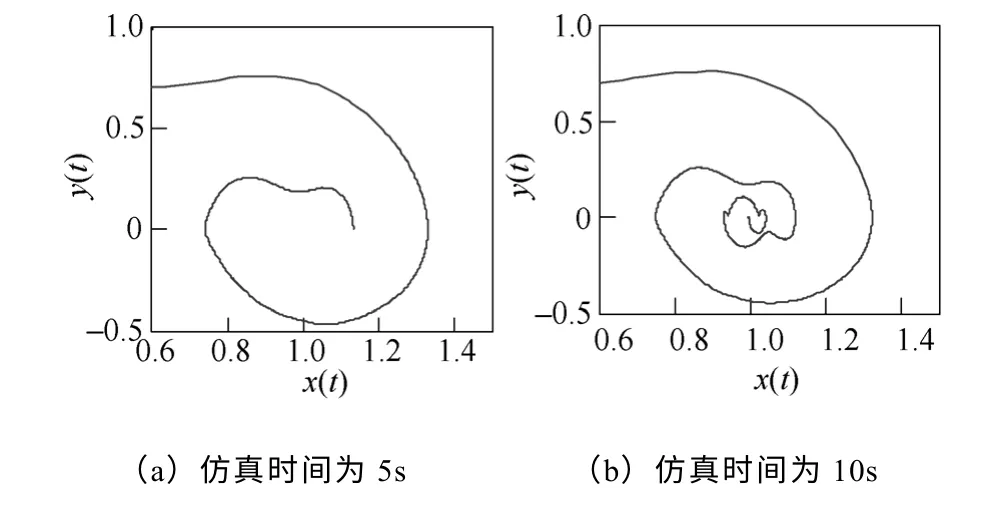
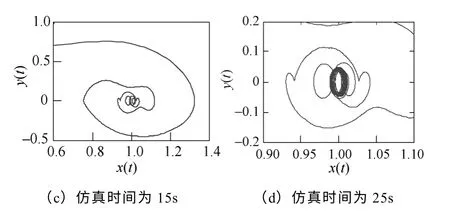
图9 复合测试信号2 的相轨迹Fig.9 Phase trajectory of the input composite test signal 2

2.3.3 复合测试信号3

图10为Kunder 四机两区域系统接线图，具体参数见文献[14]，基于Matlab 平台搭建仿真系统。采用白噪声激励G1的励磁模块参考电压，作用时间为20s。采集G4的相对功角摇摆曲线，如图11所示。

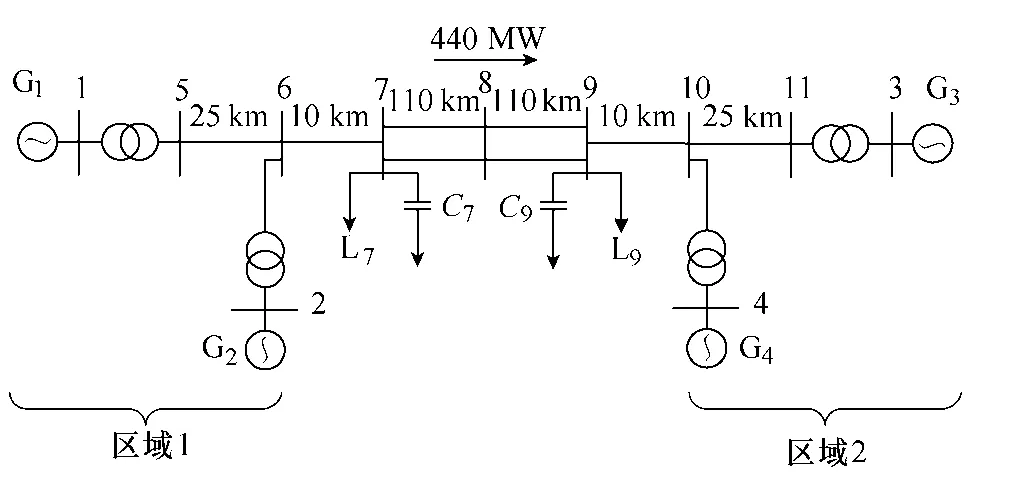
图10 四机两区域系统接线图Fig.10 Four machine two area system wiring diagram

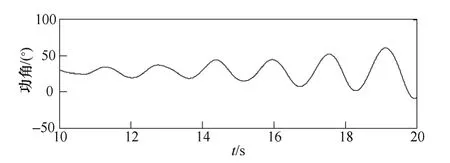
图11 G4相对功角振荡曲线Fig.11 G4relative power angle oscillation curve

G4的相对功角摇摆曲线归一后乘以0.1 的系数输入到可停振动系统中，得到其相轨迹如图12所示。此相轨迹以初值螺旋发散，从增幅的小周期状态，进入多周期状态可以判断信号中包含有发散振荡信号。

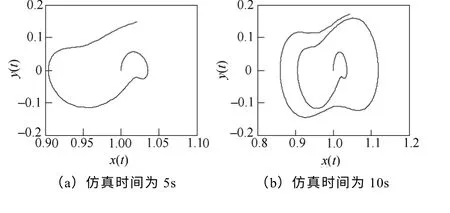
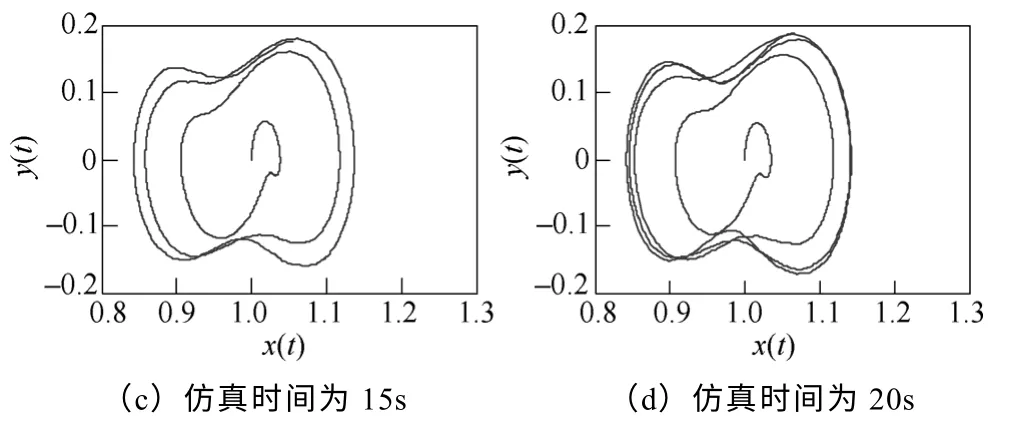
图12 G4相对功角振荡曲线的相轨迹Fig.12 Phase trajectory of G4relative power angle oscillation curve

利用中国电力科学研究院的PSD-SSAP 小干扰稳定分析模块，进行特征值分析，计算得到的区域间模式模态、其振荡频率和阻尼比见表1。表1 证明了该系统对这两种区域间的阻尼严重不足，是负阻尼类型的低频振荡。

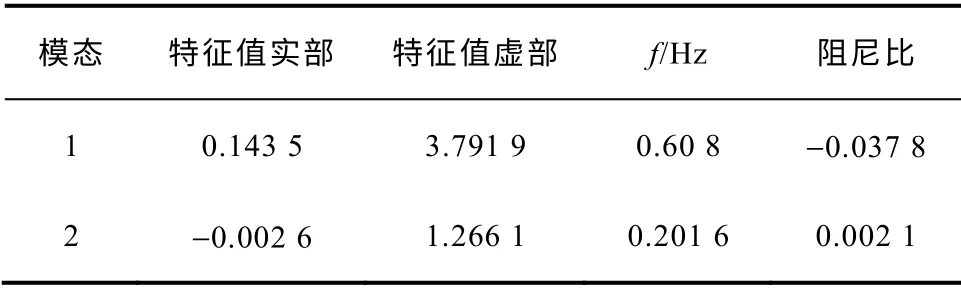
表1 特征值计算结果Tab.1 The results of eigen values computation

综上，强迫功率振荡相轨迹是以初值螺旋收缩为极限环。弱阻尼模式低频振荡的相轨迹是以初值螺旋收缩为单个点。本文将这两种模式定义为“低频振荡吸引子”。负阻尼模式低频振荡的相轨迹是以初值螺旋发散，由增幅的小周期状态进入多周期状态，文中定义为“低频振荡排斥子”。因此，将电力系统的实测信号归一化后，乘以比例系数（＜0.36），输入到可停系统，根据其输出信号的相轨迹，是聚焦于一点，还是存在“低频振荡吸引子”或“低频振荡排斥子”就可以监测是否发生了低频振荡，而且可以判断是何种机理模式的低频振荡，并得到该模式的阻尼特性。

3 低频振荡监测的步骤

3.1 自动识别算法

图形变化的特征识别需要人的参与，为了自动给出计算机可识别的定量指标满足自动监测的要求，本文提出了一种定量的自动识别算法。分别计算相轨迹中各点与其平衡点（1,0）的欧氏距离（Euclidean distance）的期望值及其对数距离，文中简称为平衡距dav和对数平衡距dlog（logarithm distance with equilibrium point）。平衡距

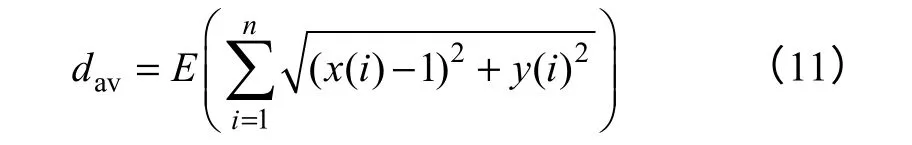
对数平衡距

不同强度白噪声、周期信号及含噪周期信号的相轨迹的对数平衡距如图13所示。其中，曲线1、2 和3 为白噪声，噪声强度分别为和1（D为噪声强度）。曲线4 为图2的周期信号。曲线5、6 为图3信噪比为3.01dB 和−9.03dB 的带噪周期信号。

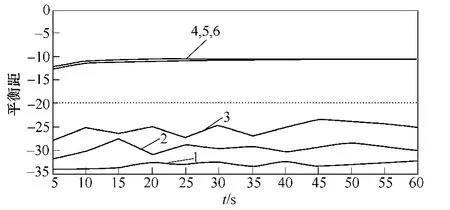
图13 白噪声、周期信号及含噪周期信号的 对数平衡距Fig.13 dlogof white noise,periodic signal and periodic signal white noise

由图13可知，白噪声、周期信号（包括含噪周期信号）的对数平衡距dlog明显分成两类。第一类为白噪声相轨迹图（曲线1～曲线3），其dlog在−25dB以下波动，即可以判定输出为可停状态。第二类为周期信号相轨迹的dlog为−15～10dB 之间的一个稳态值，对应为小尺度周期状态。对比图13中曲线4～曲线6 可知，噪声对周期信号的dlog的影响不大。通过大量的仿真并考虑到一定的裕度，将信号的相轨迹图的dlog＜−20dB 判定为可停状态。

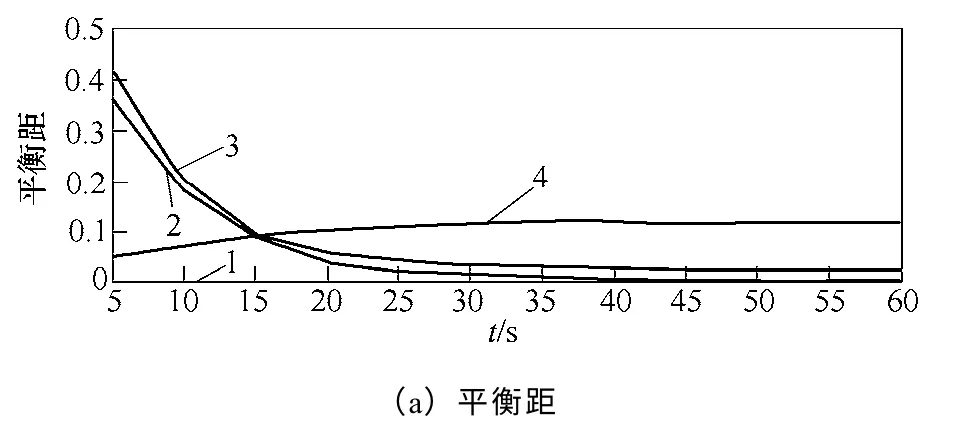
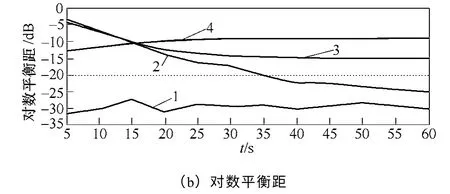
图14 白噪声、弱阻尼、负阻尼和强迫功率振荡的 平衡距和对数平衡距Fig.14 davanddlogof white noise,weak damping, negative damping signal and forced oscillation

从图14中可见，曲线1～曲线4 存在着较明显的差异，白噪声相轨迹图的平衡距dav在0 附近波动，负阻尼低频振荡的dav和dlog为先增加后稳定为稳态值。弱阻尼的低频振荡和强迫振荡的dav和dlog都是持续衰减，前者衰减到可停状态，后者衰减到小尺度周期状态。

3.2 低频振荡监测的步骤

主要包括三部分：

（1）数据预处理。将PMU 采集得到的信号经过低通滤波器，截止频率为2.5Hz。

（2）自动识别算法。预处理后的信号输入到Duffing 振子可停振动系统，得到其相轨迹。每间隔一定的时间（2～5s）计算dlog值判断状态。

①dlog稳定在一个小的值，且dlog＜−20dB，相轨迹聚焦于一点，处于可停状态，未发生低频振荡。

②dlog持续下降，30s 内衰减到−20dB 以下，或30s 仍旧下降，且dlog＜−15dB。存在“低频振荡吸引子”，吸引子是单个点，为弱阻尼低频振荡。

③dlog衰减小尺度周期状态的稳态值基本不变，或30sdlog＞−15dB。吸引子为稳定极限环，为强迫功率振荡。

④dlog为先增加后稳定为稳态值，存在“低频振荡排斥子”，为负阻尼的低频振荡。

（3）结合其他方法对振荡频率、阻尼比、振型进行识别。

4 仿真及实例分析

4.1 实例一

图15为南方电网在丰大运行方式下，对系统施加小扰动，用BPA 稳定计算程序得到的贵天线（贵阳变—天生桥II 级）的有功功率时域仿真图形[15,16]。输入到可停振动系统中分析，得到其相轨迹和对数平衡距如图16所示。

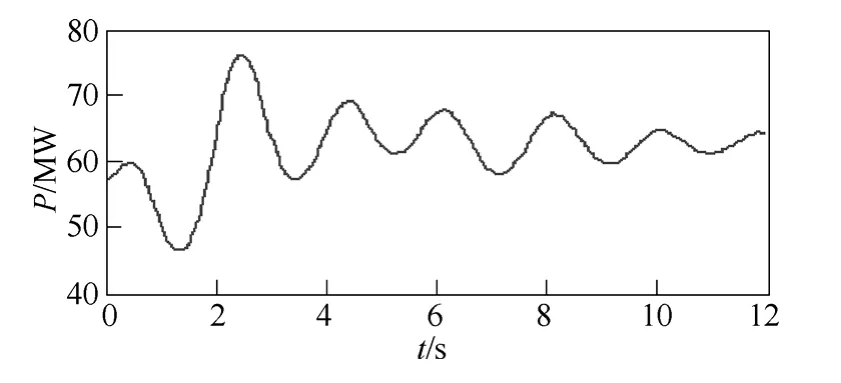
图15 贵天线功率振荡曲线Fig.15 Power oscillation waveform of Gui-Tian transmission system

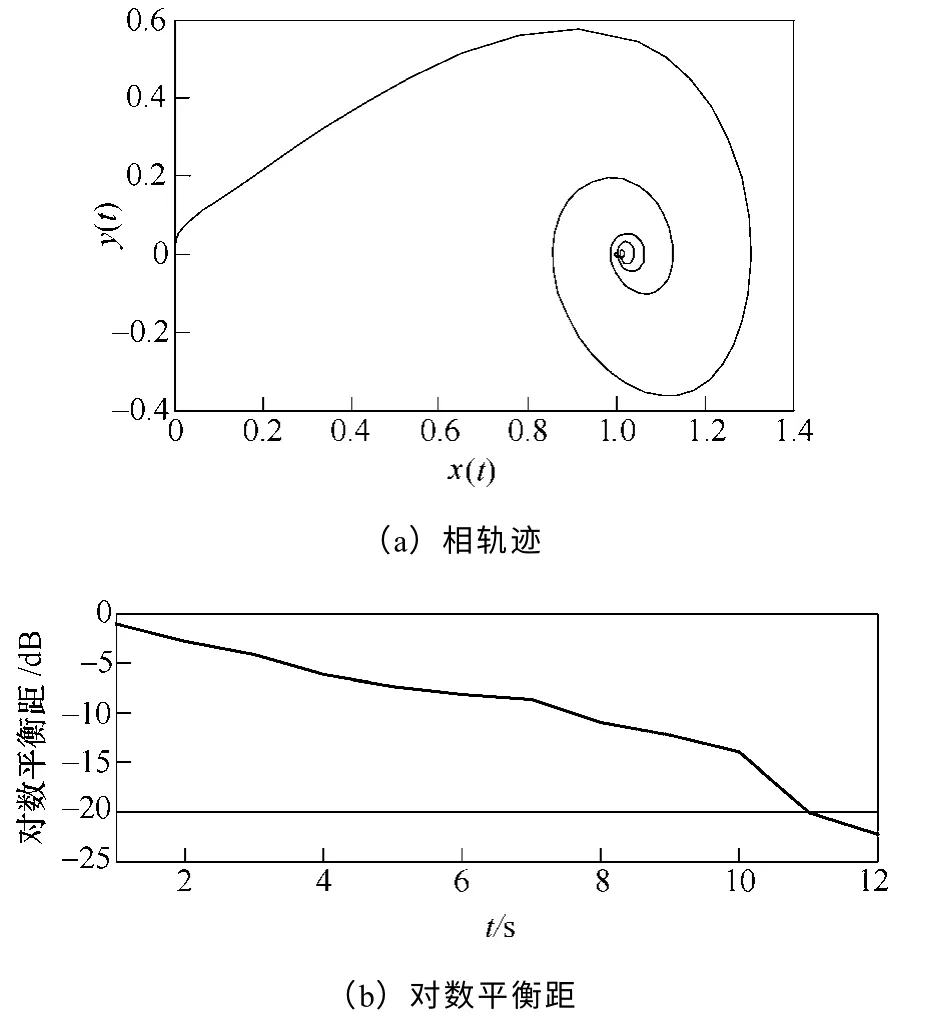
图16 贵天线功率振荡曲线的相轨迹和对数平衡距Fig.16 Phase trajectory anddlogof power oscillation waveform of Gui-Tian transmission system

图16以初值螺旋收缩，存在“低频振荡吸引子”，吸引子是单个点，其dlog12s 内衰减到−20dB以下，为弱阻尼模式的低频振荡。采用随机子空间的方法进行辨识[17]，得出振荡模式的振荡频率和阻尼比，具体见表2。表2 证明了该系统对这两种区域间的阻尼不足，是弱阻尼模式的低频振荡。

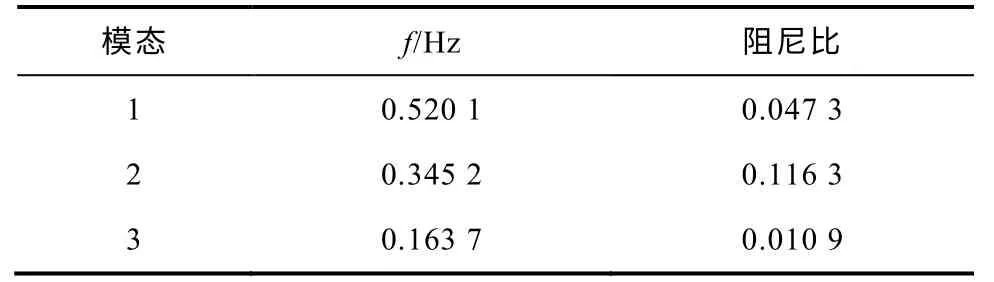
表2 低频振荡模态分量参数Tab.2 Parameters of low frequency oscillation model functions

4.2 实例二

采用南方电网作为研究对象。图17为云南小湾机组存在频率为 0.496Hz 的周期性机械功率扰动时，小湾机组与广东大亚湾机组的功角振荡曲线。

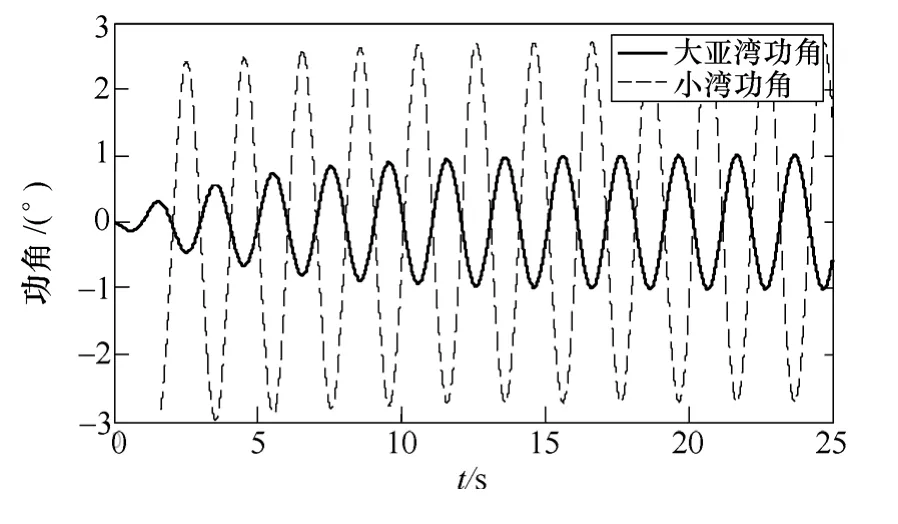
图17 小湾、大亚湾机组功角振荡曲线Fig.17 Power-angle oscillation of XW,DYW generators

图18为大亚湾和小湾功角振荡曲线输入到可停振动系统中得到的相轨迹。该相轨迹以初值螺旋收缩为封闭圆环，存在“低频振荡吸引子”，吸引子为稳定极限环，dlog15s 衰减到稳态值−10dB，可以判断为强迫功率振荡，应该迅速找到并切除扰动源。

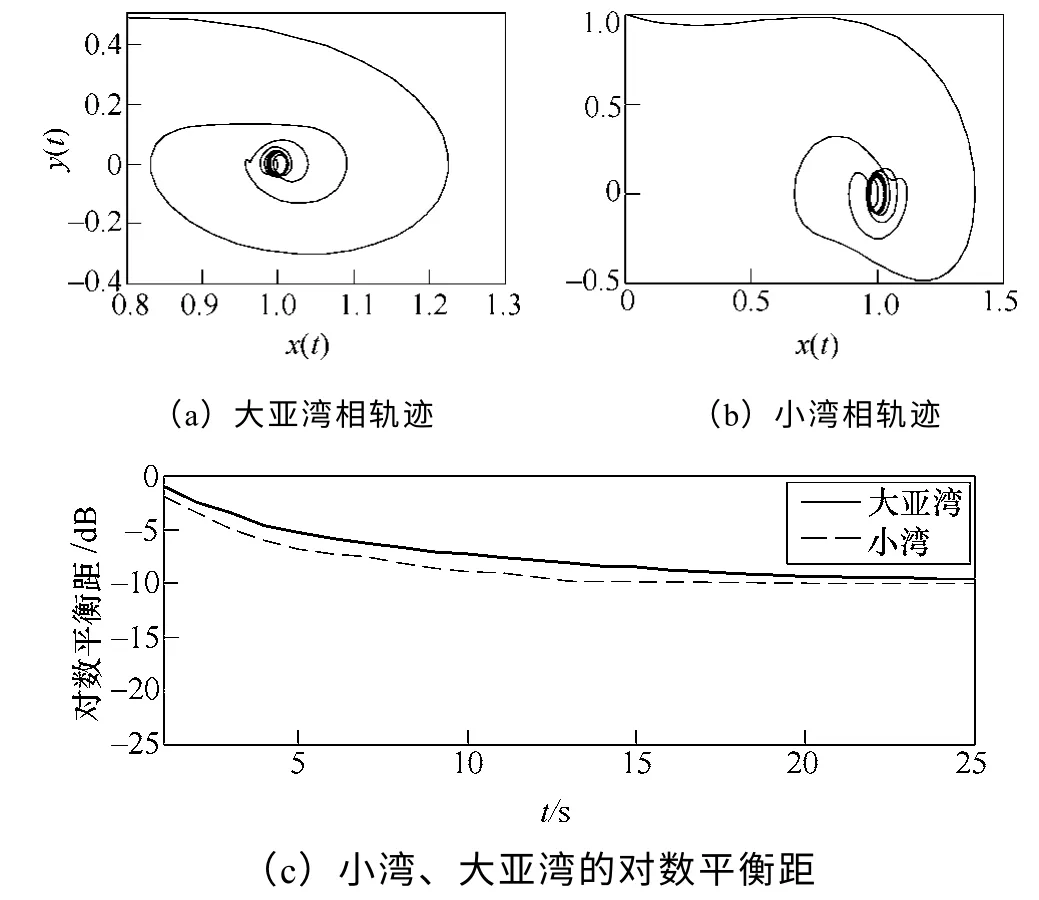
图18 小湾、大亚湾机组功角振荡曲线的相轨迹Fig.18 Phase trajectory anddlogof power-angle oscillation of XW,DYW generators

5 结论

本文将Duffing 可停系统理论应用于电力系统低频振荡的监测中。该方法的核心思路是将端口上的量测信号输入到可停系统中，根据输出的相轨迹是聚焦为一点还是存在低频振荡吸引子或排斥子来判断是否发生低频振荡，是何种机理模式、阻尼特性的低频振荡。与其他方法（prony、HHT 和原子稀疏分解等）相比，该方法是一种可视化的图像分析方法。具有实时和可视化的优点，且对噪声具有免疫力，为后期低频振荡参数定量识别，提供预判的依据。

[1]智勇,王官宏,肖洋,等.750kV 线路投运后甘肃电网动态稳定性分析[J].电力系统保护与控制,2011,39(3):114-118.

Zhi Yong,Wang Guanhong,Xiao Yang,et al.Dynamic stability analysis of Gansu power grid after 750kV lines was put into operation[J].Power System Protection and Control,2011,39(3):114-118.

[2]李勋,龚庆武,贾晶晶,等.基于原子稀疏分解的低频振荡模态参数辨识方法[J].电工技术学报,2012,27(9):124-131.

Li Xun,Gong Qingwu,Jia Jingjing,et al.Atomic sparse decomposition based identification method for low-frequency oscillation modal parameters[J].Trans- actions of China Electrotechnical Society,2012,27(9):124-131.

[3]贾勇,何正友.基于受扰轨迹的低频振荡分析方法综述[J].电力系统保护与控制,2008,40(11):140-148.

Jia Yong,He Zhengyou.Review on analysis methods for low frequency oscillations based on disturbed trajectories[J].Power System Protection and Control,2008,40(11):140-148.

[4]汪永华,王正风.电网动态监测预警与辅助决策系统的应用与发展[J].电力系统保护与控制,2010,38(10):70-74.

Wang Yonghua,Wang Zhengfeng.Application and development of dynamic monitoring preventive alarm and auxiliary decision system[J].Power System Protection and Control,2010,38(10):70-74.

[5]马燕峰,赵书强.基于在线辨识和区域极点配置法的电力系统低频振荡协调阻尼控制[J].电工技术学报,2012,27(9):117-123.

Ma Yanfeng,Zhao Shuqiang.Coordinated damping dontrol of power pystems low-frequency oscillation based on on-line identification and region poles assignment[J].Transactions of China Electrotechnical Society,2012,27(9):117-123.

[6]戚军,江全元,曹一家.采用时滞广域测量信号的区间低频振荡阻尼控制器设计[J].电工技术学报,2009,24(6):154-159.

Qi Jun,Jiang Quanyuan,Cao Yijia.Design of damping controller for inter-area low-frequency oscillation using time-delay wide-area measurements[J].Transactions of China Electrotechnical Society,2009,24(6):154-159.

[7]Demello F.Concepts of synchronous machine stability as affected by excitation control[J].IEEE Transactions on Power Apparatus and Systems,1969,88(4):316-329.

[8]汤涌.电力系统强迫功率振荡的基础理论[J].电网技术,2006,30(10):29-33.

Tang Yong.Fundamental theory of forced power oscillation in power system[J].Power System Technology,2006,30(10):29-33.

[9]王铁强,贺仁睦,徐东杰,等.电力系统低频振荡机理的研究[J].中国电机工程学报,2002,22(2):21-25.

Wang Tieqiang,He Renmu,Xu Dongjie,et al.The mechanism study of low frequency oscillation in power system[J].Proceedings of the CSEE,2002,22(2):21-25.

[10]杨东俊,丁坚勇,邵汉桥.基于WAMS 的负阻尼低频振荡与强迫功率振荡的特征判别[J].电力系统自动化,2013,37(13):57-62.

Yang Dongjun,Ding Jianyong,Shao Hanqiao.WAMS based characteristic discrimination of negative damping low-frequency oscillation and forced power oscillation[J].Automation of Electric Power Systems,2013,37(13):57-62.

[11]周薛雪,赖莉,罗懋康.基于分数阶可停振动系统的周期未知微弱信号检测方法[J].物理学报,2013,62(9):1-13.

Zhou Xuexue,Lai Li,Luo Maokang.A new detecting method for periodic weak signals based on fractional order stopping oscillation system[J].Acta Physic Sinica 2013,62(9):1-13.

[12]朱卫秋.非线性随机动力系统与控制[M].北京:科学出版社,2003.

[13]张芷芬,丁同仁,黄文灶,等.微分方程的定性理论[M].2 版.北京:科学出版社,1997.

[14]Kundur P.Power System Stability and Control[M].NewYork:McGraw-Hill,1994.

[15]李兴源,刘红超,任晓莹,等.天生桥-广州交直流并联运行对贵州电网的影响[R].贵州省电力工业局,1997.

[16]刘红超,李兴源.基于PRONY 辨识的交直流并联输电系统直流阻尼控制的研究[J].中国电机工程学报,2002,22(7):54-57.

Liu Hongchao,Li Xingyuan.Study of DC damping control in AC/DC transmission systems based on prony method[J].Proceedings of the CSEE,2002,22(7):54-57.

[17]Ni J M,Shen C,Liu F.Estimation of the electromechanical characteristics of power systems based on a revised stochastic subspace method and the stabilization diagram[J].Science China Techno- logical Sciences 2012,55(6):1677-1687.