网侧三相PWM整流器最小耦合模型控制

吴轩钦 谭国俊 何凤有 曹晓冬

（中国矿业大学信息与电气工程学院 徐州 221008）

0 引言

基于三相电压型脉宽调制（Pulse Width Modulation，PWM）整流器拓扑结构的网侧功率变换器广泛应用于新能源发电、有源滤波器（APF）、不间断电源（UPS）、交流传动（ED）、高压直流输电（HVDC）及统一潮流控制（UPFC）等领域[1-3]。作为发（用）电系统与电网之间的桥梁，网侧功率变换器控制策略的优劣直接决定了系统的运转方式和性能。从目前查阅的文献来看，主要有间接电流控制[4]、直接电流控制[5-11]、直接功率控制（Direct Power Control，DPC）[12-14]以及以模型预测控制（Model Predictive Control，MPC）[15-17]和反馈线性化控制（Feedback Linearization Control，FLC）[18,19]为代表的基于现代控制理论的控制策略[20]。

纵观上述控制策略，间接电流控制存在参数鲁棒性差、动态过程电流变化剧烈和稳定性差等缺点；直接功率控制主要存在开关频率不固定的缺陷以及无功功率波动问题；基于现代控制理论的控制策略存在控制算法过于复杂问题。基于矢量定向的直接电流控制策略是目前比较成熟而且应用最为广泛的控制方式[3]。基于矢量定向的直接电流控制策略在同步旋转坐标系下对PWM 整流器进行建模分析，其控制关键在于定向矢量信息（幅值和相位）的准确获取。根据定向矢量的不同，现有的方法可分为电网电压定向控制（Voltage Oriented Control，VOC）和虚拟电网磁链定向控制（Virtual Flux Oriented Control，VFOC）。文献[3,21]对上述两种定向方法进行深入的对比研究，认为电网电压定向方式物理概念清晰，但附加的网侧电压传感器增加硬件成本及故障点，同时非理想电网条件下极易引发定向误差。虚拟电网磁链矢量定向方式可实现无网侧电压传感器控制，提升系统可靠性，同时对谐波和干扰具有良好的抑制作用[3,21]。

基于上述两种定向矢量的直接电流控制策略通常在dq 同步旋转坐标系下对PWM 整流器进行建模分析，但坐标的旋转变换导致dq 同步旋转坐标系下的数学模型存在交叉耦合问题，影响系统的动、静态性能。为此，学者们进行了大量的研究分析。文献[6]以电网电压作为定向矢量，提出采用d、q 轴电流前馈控制策略以补偿交叉耦合项，该策略在一定程度上提高了整流器的动、静态特性，但无法真正达到动、静态解耦的目标。文献[10]在虚拟电网磁链定向PWM 整流器矢量控制基础上提出的电流前馈控制策略同样未从根源上消除交叉耦合项影响，虚拟电网磁链定向方式下的数学模型在 d、q轴上依旧包含交叉耦合分量。需要指出的是，文献[22]在两相静止坐标系下实现PWM 整流器数学模型完全解耦，但为实现交流量的稳态无误差调节所采用的谐振调节器会引入相角滞后，不利于系统的稳定，并非最优方案。

从目前研究情况来看，为提高基于矢量定向PWM 整流器直接电流控制的动、静态性能，现有的控制策略通常采用前馈补偿方法，未以数学模型为出发点考虑，进而也未从根源上消除或削弱交叉耦合量影响。

不同于上述方法，本文引入“虚拟定子磁链”概念，提出PWM 整流器最小耦合模型控制策略。围绕所提控制策略，建立了虚拟磁链定向方式下PWM 整流器数学模型，并与传统的虚拟电网磁链定向方式进行深入对比分析。同时提出了虚拟定子磁链定向控制方式下直接电流控制和功率因数控制方法。为保证控制策略的有效实施，构建了频率自适应虚拟定子磁链观测模型。仿真分析和实验效果验证了所提控制策略可实现动、静态最小耦合控制目标，提升了系统的控制性能。

1 PWM 整流器虚拟定子磁链概念

本文以图1所示的基于三电平电压型PWM 整流器拓扑结构的网侧功率变换器作为研究对象，结合交流电机学理论，电网电压、虚拟气隙磁链分别等效为交流电机感应电动势和气隙磁链，PWM 整流器交流侧电压、虚拟定子磁链等效为交流电机定子电压和定子磁链。因此从等效观点层面分析，通常意义上的“虚拟电网磁链定向控制”更为准确的表述应该为“虚拟气隙磁链定向控制（Virtual Air-Gap Flux Oriented Control，VAFOC）”。本文借鉴交流电机矢量控制思想，开展PWM 整流器虚拟定子磁链定向控制（Virtual Stator Flux Oriented Control，VSFOC）研究。同时对文中物理量做如下规定，u、i、ψ、R、L分别表示电压、电流、磁链、电阻和电感；下标a、b、c 表示abc 坐标系下的分量；下标α、β表示αβ坐标系下的分量；下标d、q表示dq 坐标系下的分量；ω为旋转角频率；下标首字符g、c分别表示电网和功率变换器端口。

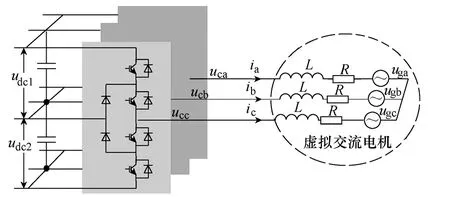
图1 三电平PWM 整流器等效虚拟电机示意图Fig.1 The schematic diagram of three-level PWM rectifier equivalent to virtual motor

根据上述等效概念，虚拟气隙磁链ψg以电网同步角频率ωg旋转，且电网电压ug与虚拟气隙磁链ψg之间满足关系[10]

对式（1）两边微分，可得

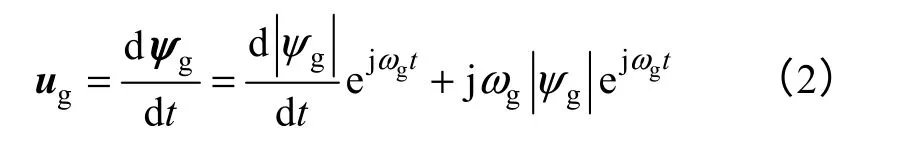
忽略线路杂散电阻R，电网电压ug与整流器交流侧电压uc之间的关系可表示为

将式（3）代入式（1），并结合上述PWM 整流器与交流电机的等效概念，可得虚拟气隙磁链ψg与虚拟定子磁链ψc之间的关系为

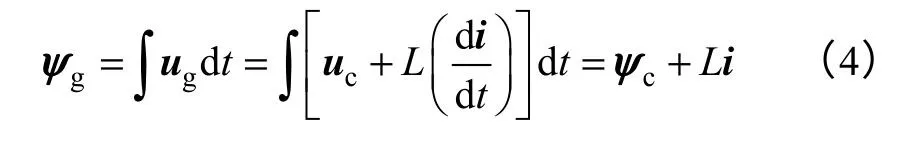
式（4）在αβ坐标系下可表示为

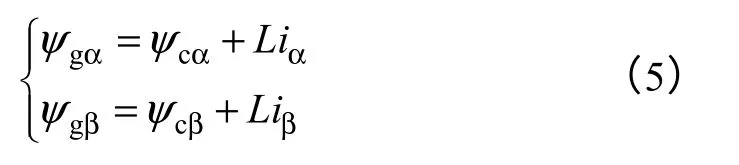
结合以上分析及式（3）～式（5）可得如图2所示的引入虚拟定子磁链的PWM 整流器矢量关系图。图2中，ωc为虚拟定子磁链矢量ψc的旋转角速度、θc为ψc与α轴的夹角、ϕgc为ψc与ψg之间的夹角。

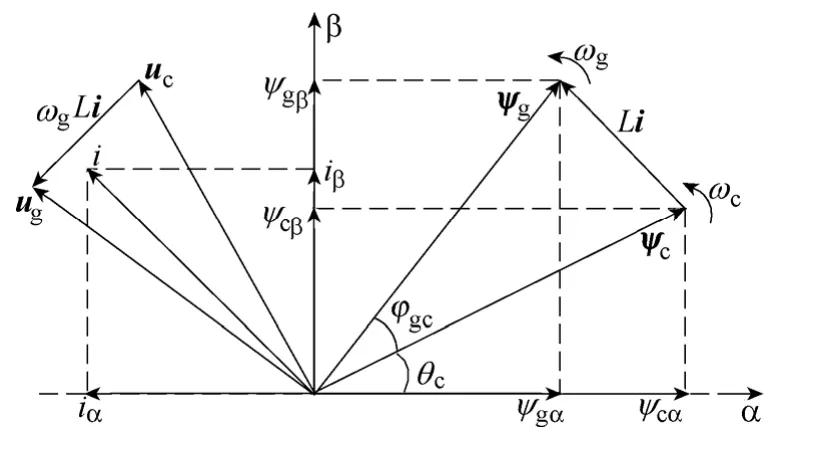
图2 PWM 整流器矢量关系Fig.2 Vector diagram of PWM rectifier

2 PWM 整流器虚拟定子磁链定向模型

将d 轴定向在虚拟定子磁链矢量ψc方向上，则PWM 整流器交流侧数学模型为

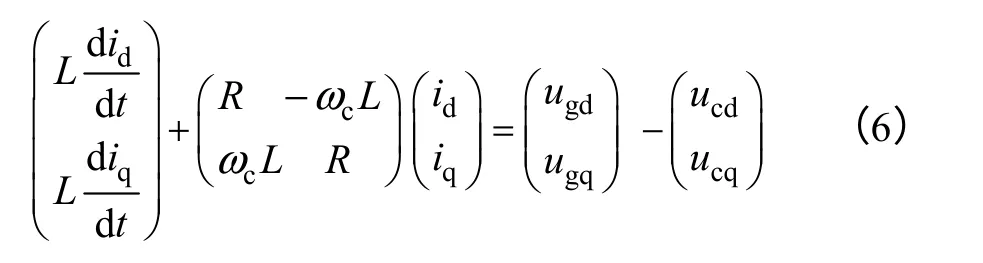
根据式（6）所示关系，并结合图2的矢量关系图，可得如图3所示的PWM 整流器VSFOC 方式下的稳态矢量图（忽略杂散电阻R）。稳态情况下d|ψg|/dt=0，由式（2）可得

由于d 轴定向ψc方向上，则ψcd=|ψc|，ψcq=0，将式（4）代入式（7）并变换到dq 坐标系下，可得

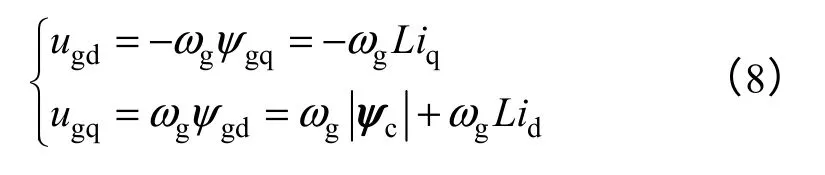
定义瞬时转差角频率ωs，并满足

将式（8）和式（9）代入式（6）可得VSFOC方式下PWM 整流器交流侧数学模型为

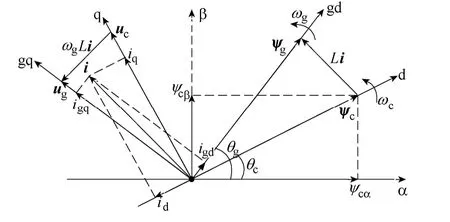
图3 PWM 整流器虚拟定子磁链定向矢量图Fig.3 Vector diagram of PWM rectifier based on virtual stator flux orientation

将式（10）表达成状态变量形式，即

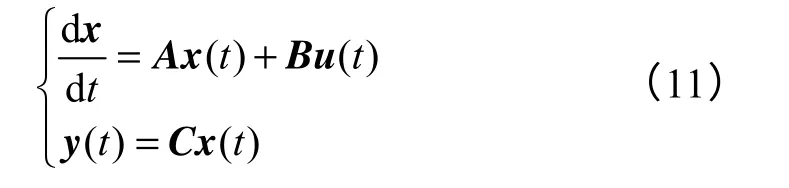
对式（11）进行Laplace 变换，得

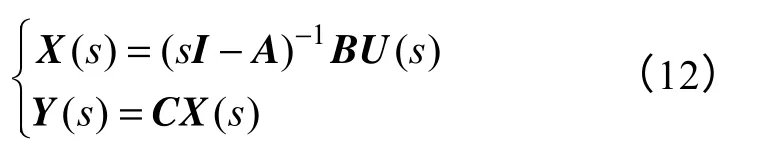
由（12）可得VSFOC 方式下PWM 整流器输入-输出模型为

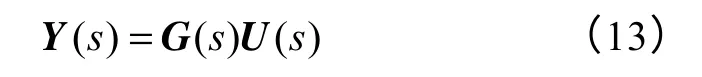
式中，G(s)=C(sI-A)−1B和C=I。参数矩阵A、B代入G(s)=C(sI-A)−1B，并将非线性变量ωs视为参数，则

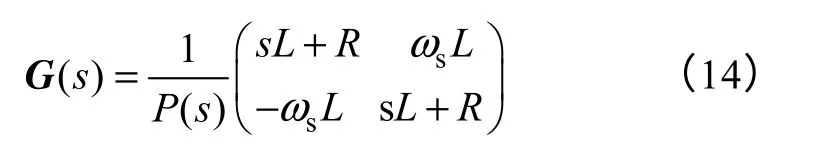
式中，P(s)=(sL+R)2+(ωsL)2。将式（14）表示为分块矩阵形式，即

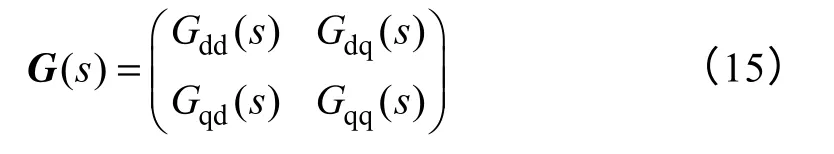
由式（15）可推导出，当ωs→0时

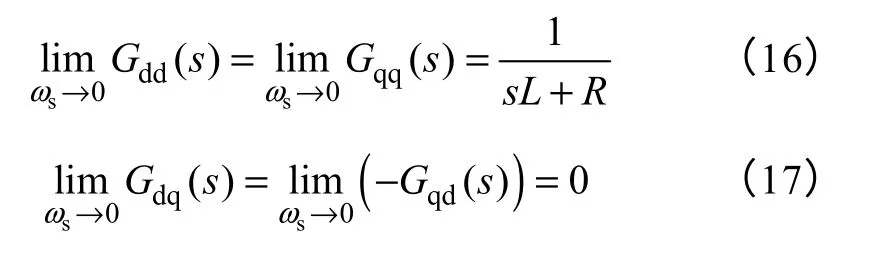
图4为当ωs→0−和ωs→0+时Gdq(s)、Gqd(s)的极限过程。从图中可以看出，随着ωs趋近于0，d、q轴之间的交叉耦合量将逼近于0，亦即PWM 整流器采用VSFOC 方式在dq 旋转坐标系下的数学模型可实现稳态完全解耦。这是与VAFOC 方式最大区别。

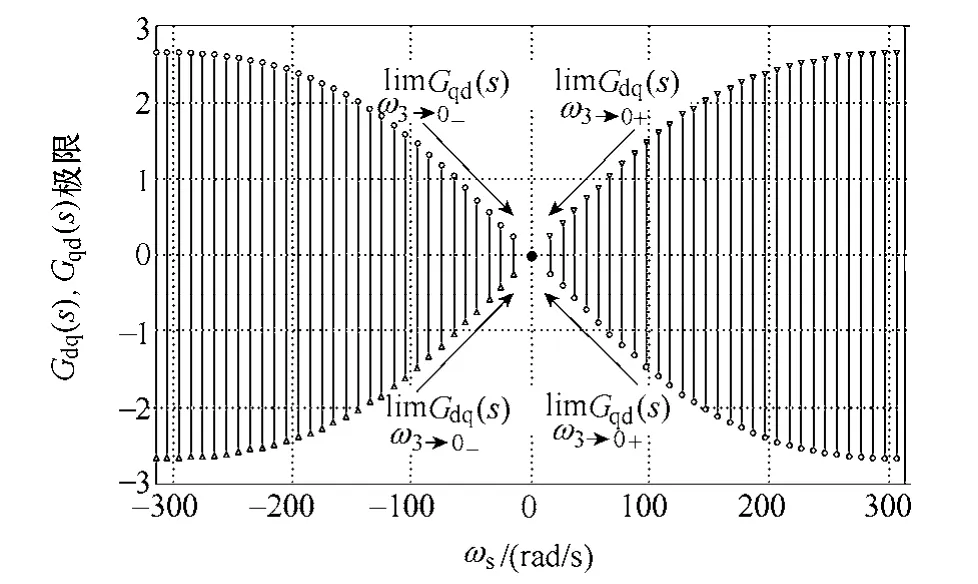
图4 当ωs→0时，Gdq(s)、Gqd(s)极限过程Fig.4 When Δω→0,the limit processofGdq(s)andGqd(s)

3 两种虚拟磁链定向方式对比分析

3.1 交叉耦合量对比分析

式（18）和式（19）为PWM 整流器上述两种不同虚拟磁链定向方式下的交流侧数学模型。其中，上标VSFO 表示虚拟定子磁链定向方式，VAFO 表示虚拟气隙磁链定向方式。

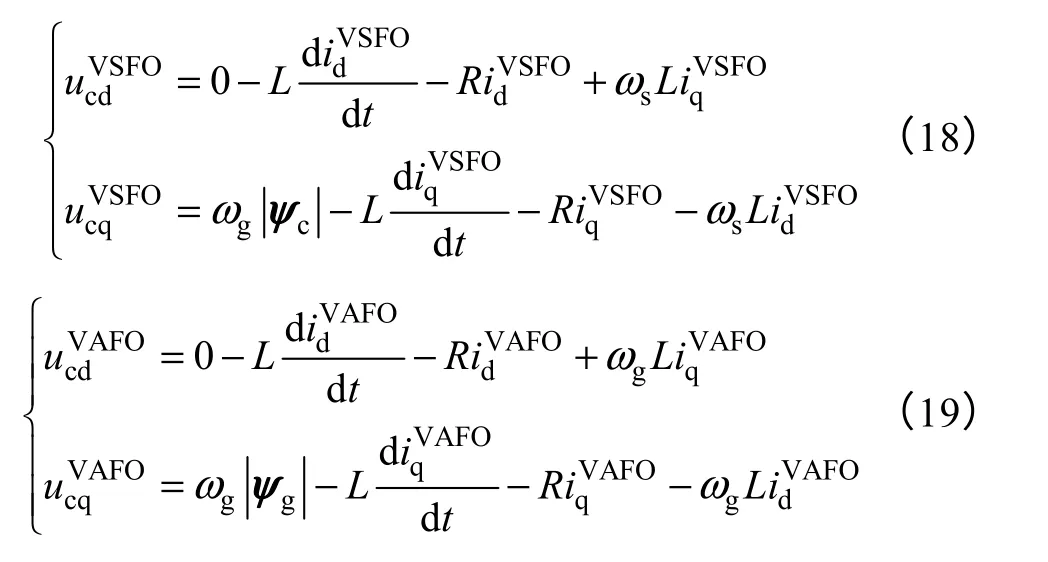
对比式（18）和式（19）可知，相比于VAFOC方式，采用VSFOC 方式时，虚拟定子磁链幅值|ψc|代替虚拟气隙磁链幅值|ψg|，同时在d、q 轴交叉耦合项中以瞬时转差角频率ωs代替电网同步角频率ωg。

根据式（6）、式（10）和式（18）可得

假设ωc的最大值为ωcmax，最小值为ωcmin。图5为虚拟定子磁链定向方式下三电平PWM 整流器大矢量V13～V18和零矢量V0所组成的电压空间矢量图。以虚拟定子磁链位于N=1 扇区（θc∈[0，π/3]）为例，有

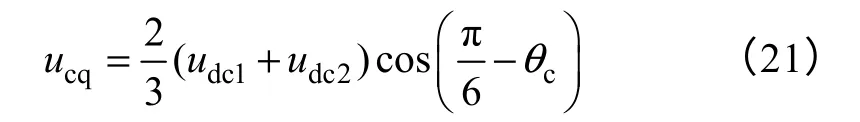
式中，udc1、udc2分别为上、下直流母线电压值。

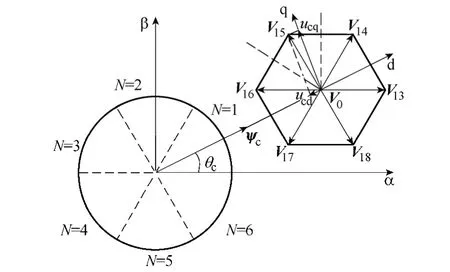
图5 三电平PWM 整流器虚拟定子磁链定向 电压空间矢量图Fig.5 Voltage space vector diagram of the three-level PWM rectifier based on virtual stator flux orientation

由式（21）可知，当θc=π/6时，ucq取得最大值ucqmax=2/3(udc1+udc2)；当零矢量V0作用时，ucq取得最小值ucqmin=0。将ucqmax、ucqmin代入式（20）可得ωc的最大值和最小值为

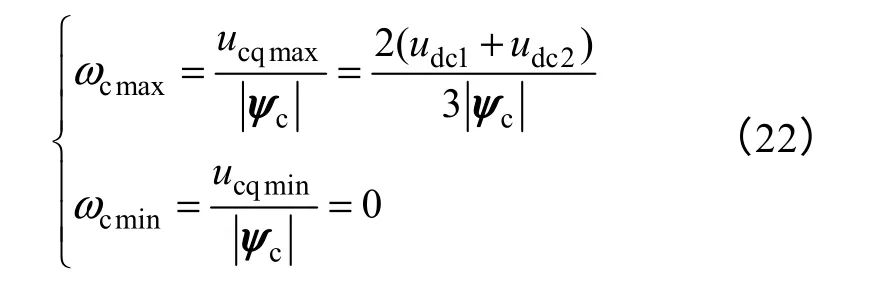
对于其他扇区，采用同样的分析方法可得同上一致的结论。结合式（20）～式（22）可得瞬时转差角频率ωs的最大值ωsmax、最小值ωsmin及取值范围为

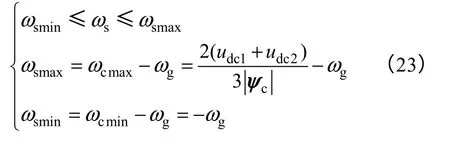
综合上述分析，PWM 整流器在VAFOC 方式下，不论系统处于稳态还是动态，d、q 轴交叉耦合量与电网旋转角频率ωg相关，并始终存在。采用VSFOC 方式，d、q 轴交叉耦合量与瞬时转差角频率ωs有关。当系统进入稳态运行阶段，ωs=0（ωc=ωg），d、q 轴交叉耦合量。在动态过程中，结合式（18）、式（19）和式（23）的分析可知，交叉耦合量与ωs相关，瞬态阶段的ωs平均值据此可知，相比于VAFOC 方式，VSFOC 方式削弱了d、q 轴间的交叉耦合。

3.2 有功电流阶跃响应对比

PWM 整流器依靠有功、无功电流的闭环控制调节有功、无功功率变化。为此，可从有功电流和无功电流的改变着手，对比分析PWM 整流器在不同虚拟磁链定向方式下的控制性能。

3.3 无功电流阶跃响应对比

4 PWM 整流器虚拟定子磁链定向控制

借鉴交流电机矢量控制思想，PWM 整流器虚拟定子磁链定向控制系统采用如图6所示的电压外环、电流内环双闭环控制方式。电压外环用来保持直流侧电压稳定，电流内环实现有功功率和无功功率的调节。

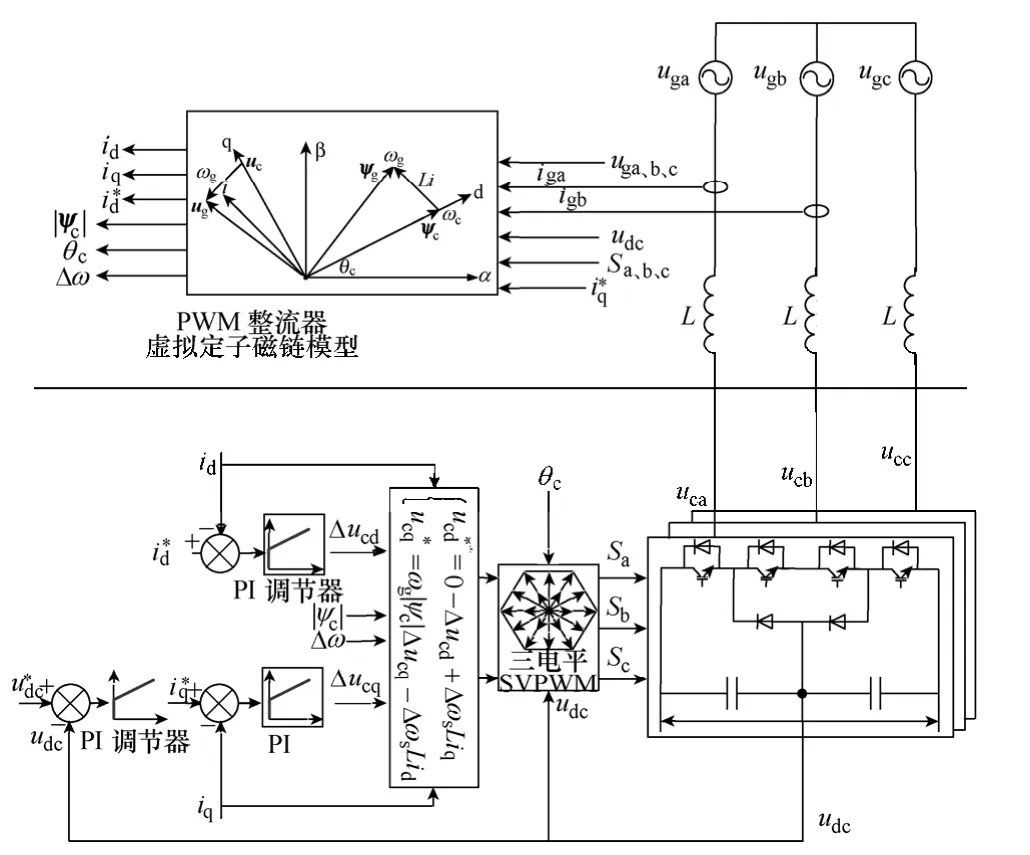
图6 PWM 整流器虚拟定子磁链定向控制Fig.6 The virtual stator-flux orientation control of PWM rectifiers

4.1 直接电流控制

在 dq 坐标系下，电流内环采用比例-积分（Proportion Integration，PI）调节器实现稳态无静差控制，根据式（10）可得VSFOC 方式下交流侧电压指令分别为

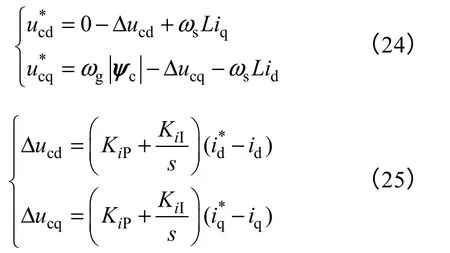
根据上述分析，可得如图7所示的PWM 整流器VSFOC 方式下直接电流控制环节。

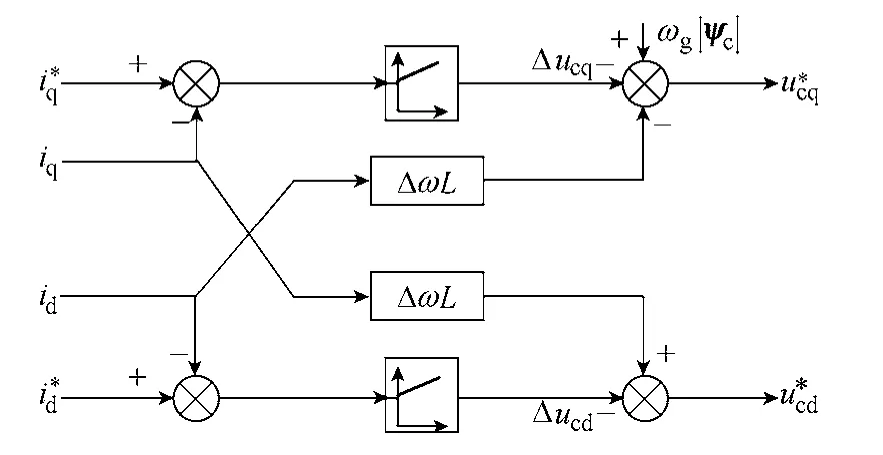
图7 PWM 整流器虚拟定子磁链定向直接电流控制Fig.7 The virtual stator-flux orientation direct-current control of PWM rectifiers

4.2 功率因数控制

从图3可知，与VAFOC 方式不同，在VSFOC方式下，无功电流id无法直接表述网侧功率因数，网侧电流在gd 轴（位于ψg方向）的分量igd则可反映网侧功率因数。在稳态情况下，网侧无功功率Q为

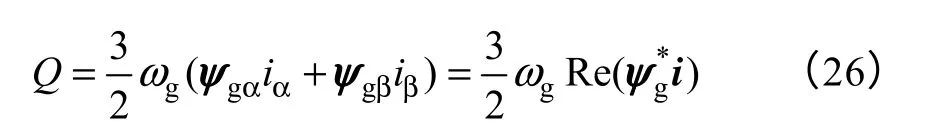
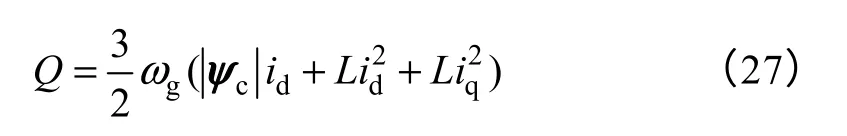
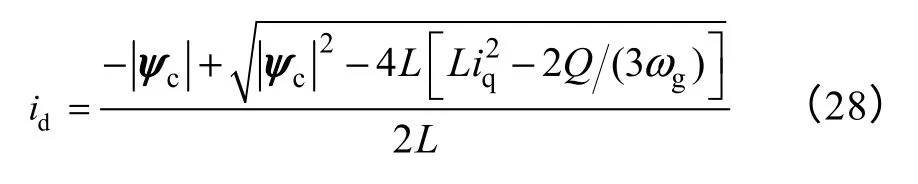
将式（28）中的Q、iq、id用其期望值Q*、、id*代替，可得VSFOC 方式下无功电流期望值为

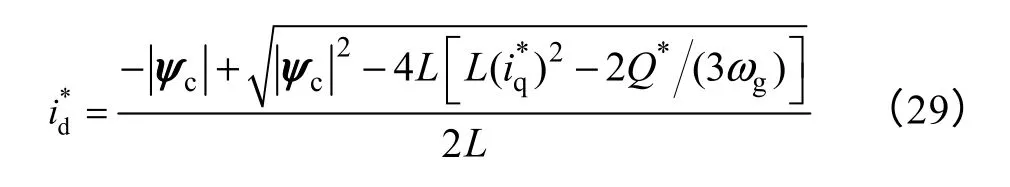
若要实现单位功率因数运行，即Q*=0，由式（29）可得为

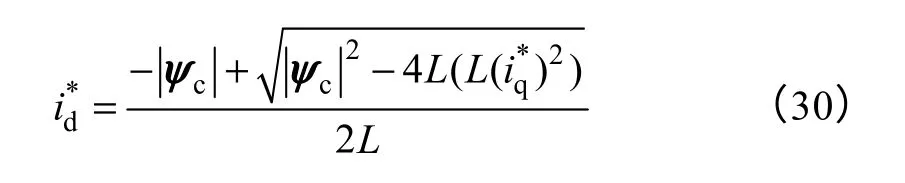
必须指出的是虚拟定子磁链定向方式采用式（30）计算无功电流期望值而引入的平方根算法将增加控制复杂性，同时表达式中引入电感参数，并与有功电流给定相关联，属于开环控制。对此，可采用无功功率闭环的方式获得无功电流期望值id*。本文为突出分析模型的耦合特性，无功电流期望值仍采用式（30）表达形式。结合图3分析，当 系统处于能馈入状态时，iq＞0，ψc滞后于ψg，ωs＜0，在单位功率因数控制作用下id＞0，igd≈0。当系统处于能量馈出状态时，iq＜0，ψc超前于ψg，ωs＞0，为实现单位功率因数控制，id＞0，igd≈0。

4.3 虚拟定子磁链频率自适应观测模型

假设电网为理想电网（ωg为恒值）。由图3和图4可知PWM 整流器实现VSFOC 的关键在于定向矢量ψc的幅值|ψc|、相位θc以及角频率ωc信息的准确获取。对此本文采用负反馈原理设计可抑制积分零点漂移的虚拟定子磁链频率自适应观测模型，其交流侧电压uc与ψc的关系为

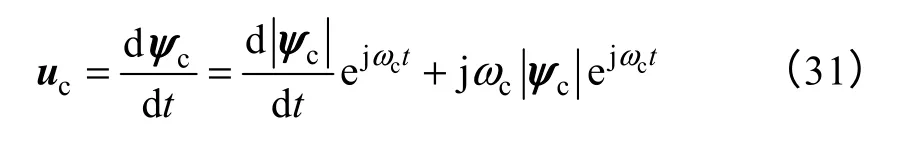
将式（31）变换到dq 坐标系下

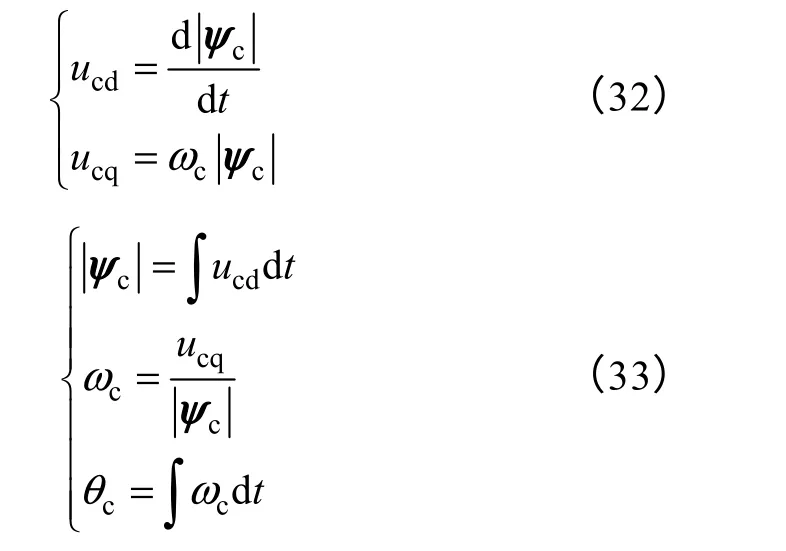
结合图3可得uc在αβ坐标系和dq 坐标系下的分量与ψc的相位θc之间满足关系

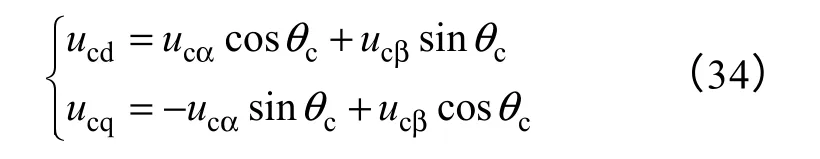
根据式（32）～式（34）可构造如图8所示的虚拟定子磁链频率自适应观测模型，模型中k为校正环节。

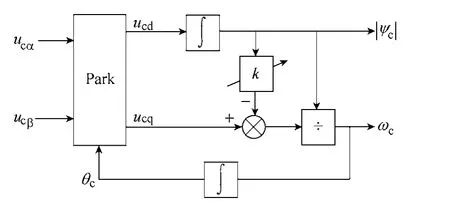
图8 虚拟定子磁链频率自适应观测模型Fig.8 The frequency adaptive observation model of the virtual stator flux

结合上述分析，虚拟定子磁链观测模型通过引入校正环节k实现θc的负反馈。由图8可知

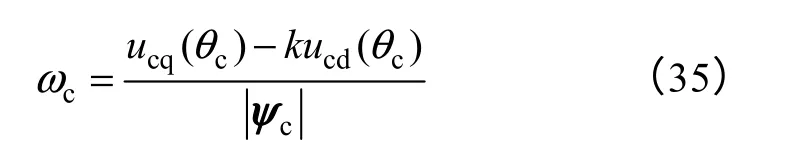
结合式（35）分析，可得虚拟定子磁链观测模型变量关系如图9所示。图9a 所示当磁场逆时针旋转（电网正序）时，ucd＜0、ucq＞0，取k＞0 可实现观测量θc的负反馈；图9b 所示当磁场顺时针旋转（电网负序）时，ucd＞0、ucq＜0，要实现θc的负反馈，必须满足k＜0。

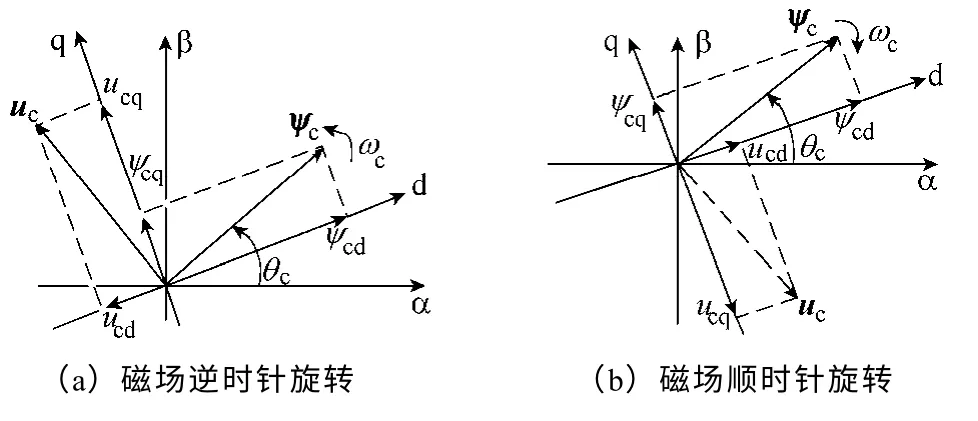
图9 虚拟定子磁链观测模型变量关系Fig.9 Relationship of variables obtained by using the virtual stator flux observer model

5 实验及结果分析

为验证本文提出的三相PWM 整流器VSFOC方案的可行性和评估这种控制方式的性能，搭建了如图10所示的双三电平功率变换器互馈实验平台。图中前端功率变换器采用双闭环控制方式，后端功率变换器以电流闭环方式运行。控制系统部分采用DSP+FPGA 架构的多核处理模式，其中DSP 为TI 公司的TMS320F28335，FPGA 为Xilinx 公司Sparten 3E。实验平台参数见下表。实验中所有观测量均经DAC 7724 转化为模拟量输出，并用安捷伦 MSO 6054A 示波器进行观测。

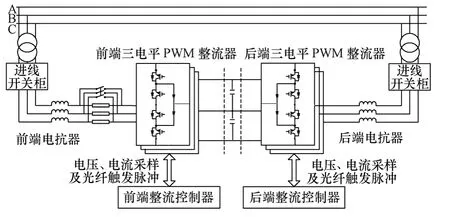
图10 双三电平功率变换器互馈实验平台Fig.10 The crossfeed testing platform of double three-level power converter

表 实验平台参数Tab. Experiment platform parameters

5.1 电流阶跃响应对比实验

为对比分析两种不同虚拟磁链定向方式下电流的响应特性，控制中未引入4.1 节所述的前馈解耦环节，同时电流内环PI 调节器参数一致。图11为 两种虚拟磁链定向方式下q 轴电流期望值阶跃变 化时系统响应对比实验波形。从图11a 可以看出，在VAFOC 方式下d 轴交叉耦合量一直存在，导致电流id需经过缓慢的调节过程才能达到期望值（=0）；图11b 所示在VSFOC 方式下，d 轴交叉 耦合量只存在于动态过程中，id只需经历短暂的调节过程便可达到稳态。实验结果与前述理论分析 一致。

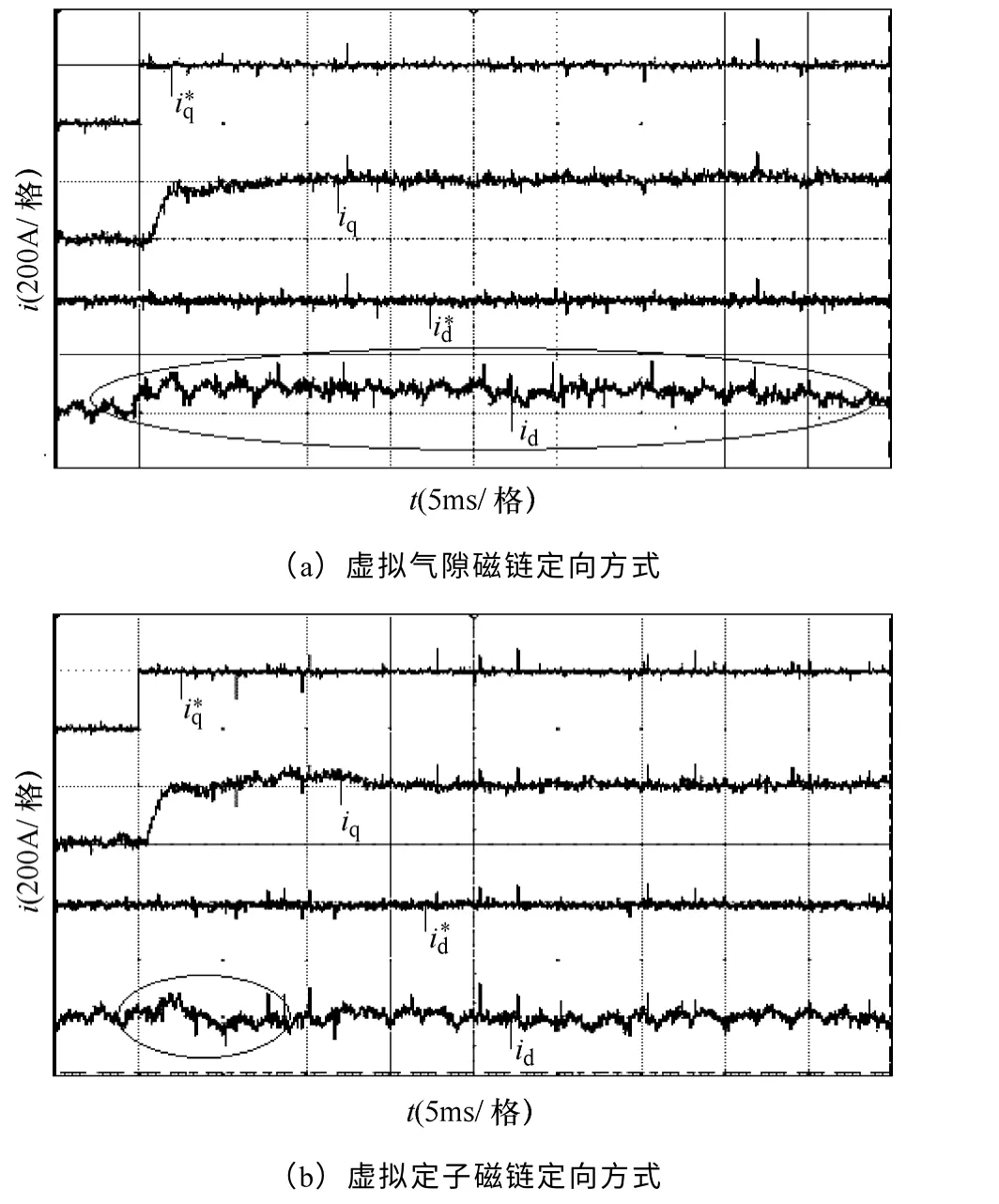
图11 q 轴电流阶跃响应对比实验波形Fig.11 The comparing experiment waveforms of current step responses in q-axis

图12为d 轴电流期望值id*阶跃变化时系统响应对比实验波形。与q 轴电流阶跃响应类似，图12a所示在VAFOC 方式下q 轴交叉耦合量一直存在，导致iq跟踪期望值（=0）的时间较为缓慢；图12b 所示在VSFOC 方式下，q 轴交叉耦合量只存在于动态过程中，iq响应迅速。

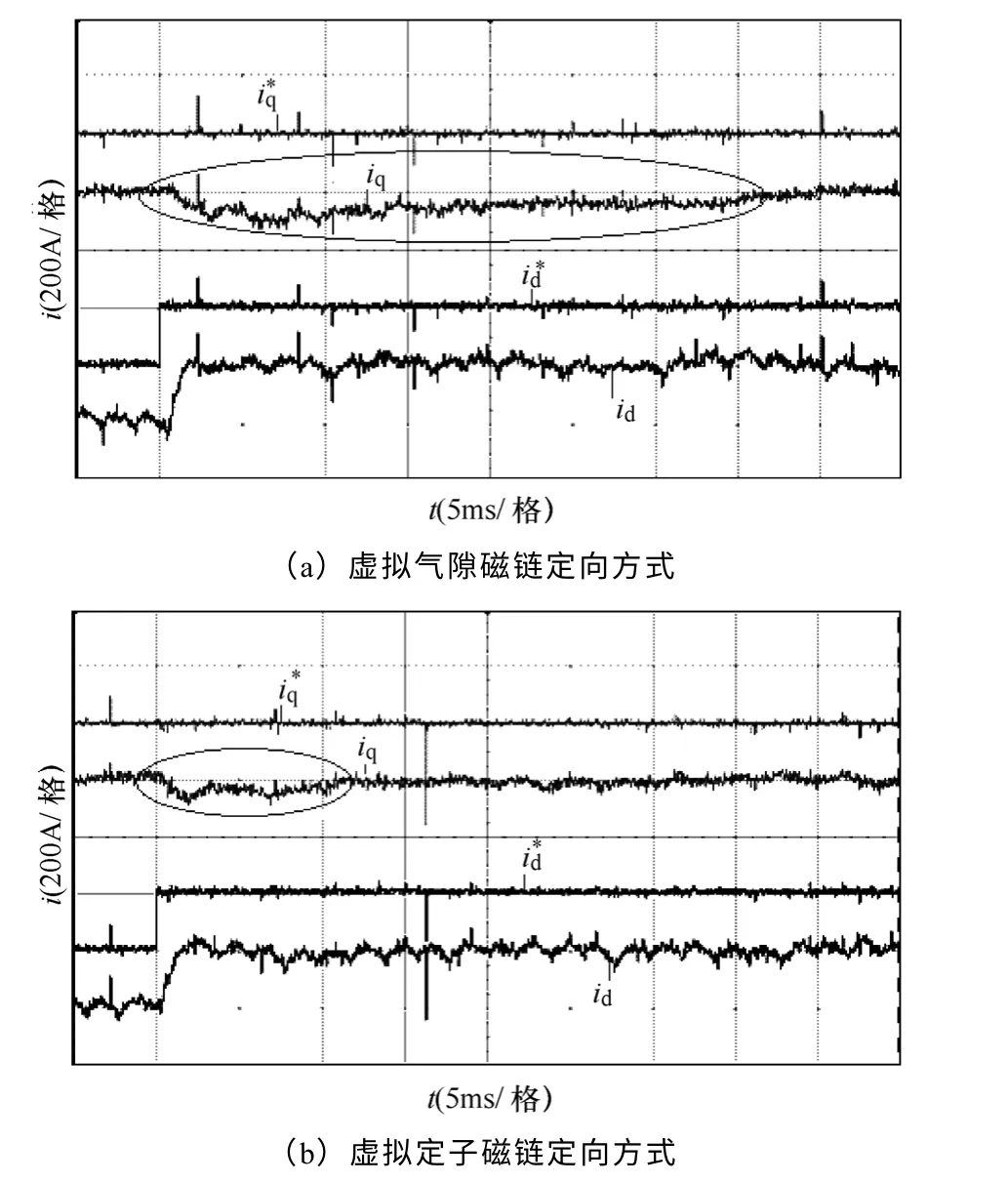
图12 d 轴电流阶跃响应对比实验波形Fig.12 The comparing experiment waveforms of current step responses in d-axis

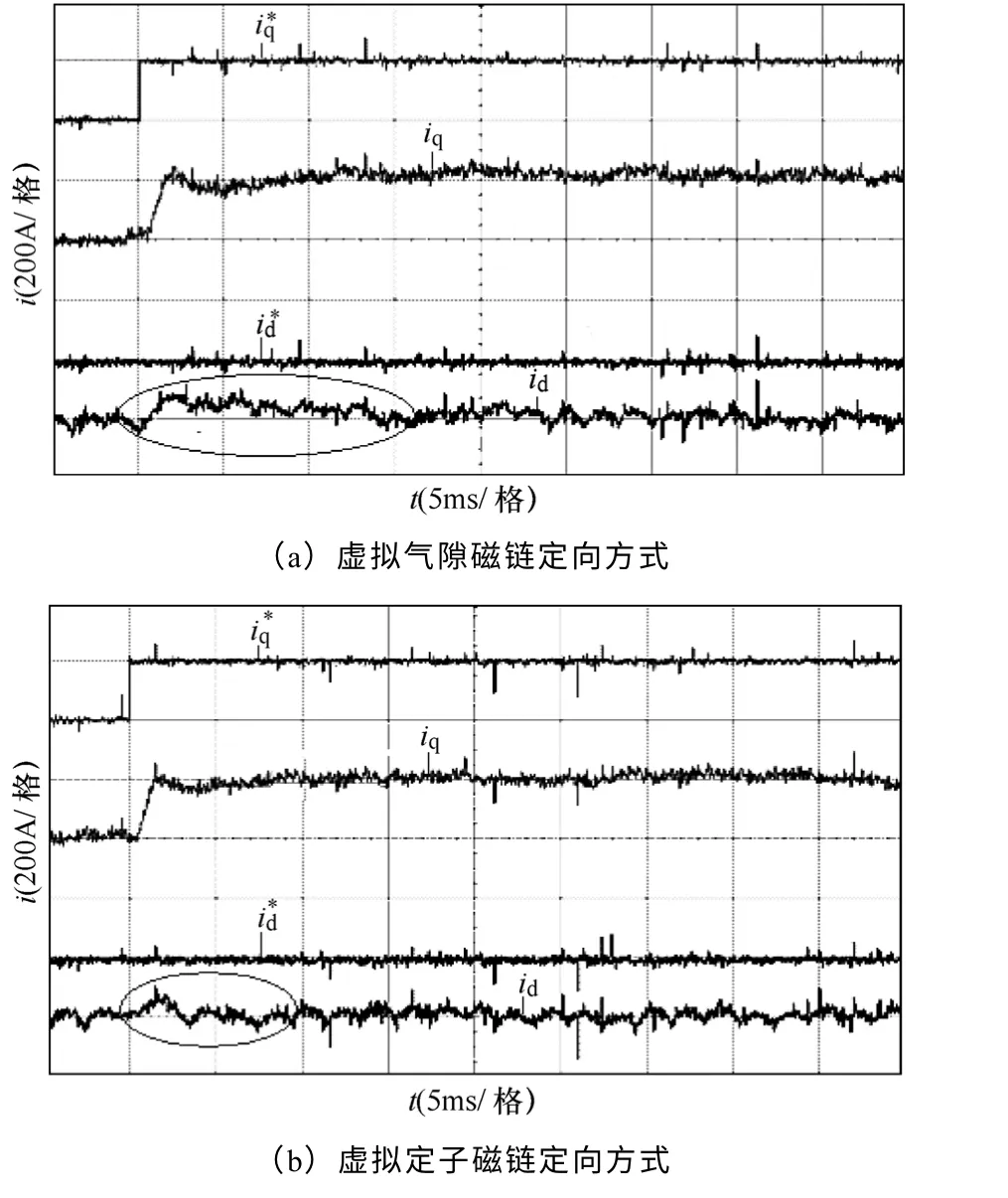
图13 加入前馈补偿q 轴电流阶跃响应对比实验波形Fig.13 The comparing experiment waveforms of current step responses in d-axis with cross-coupling feed-forward decoupling control

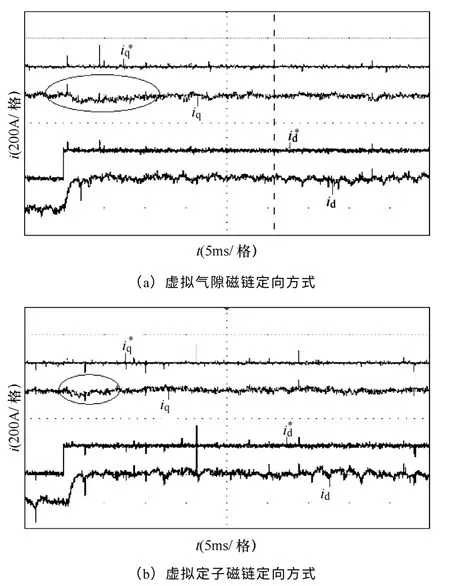
图14 加入前馈补偿d 轴电流阶跃响应对比实验波形Fig.14 The comparing experiment waveforms of current step responses in d-axis with cross-coupling feed-forward decoupling control

图13和图14为两种不同定向方式下采用图9所示的引入前馈解耦控制时d、q 轴电流阶跃响应对 比实验波形。从图中可知，两种定向方式采用前馈控制策略均可提高电流的响应速度。虚拟定子磁链定向方式的电流响应速度快于虚拟气隙磁链定向方式，这是由于在动态过程中，若采用虚拟气隙磁链定向方式，电网旋转角速度ωg保持不变，为常数，而在虚拟气隙磁链定向方式下，瞬时转差角速度Δω＜ωg，如图15所示。

5.2 虚拟定子磁链定向实验分析

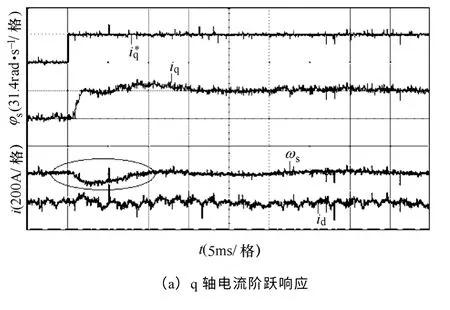
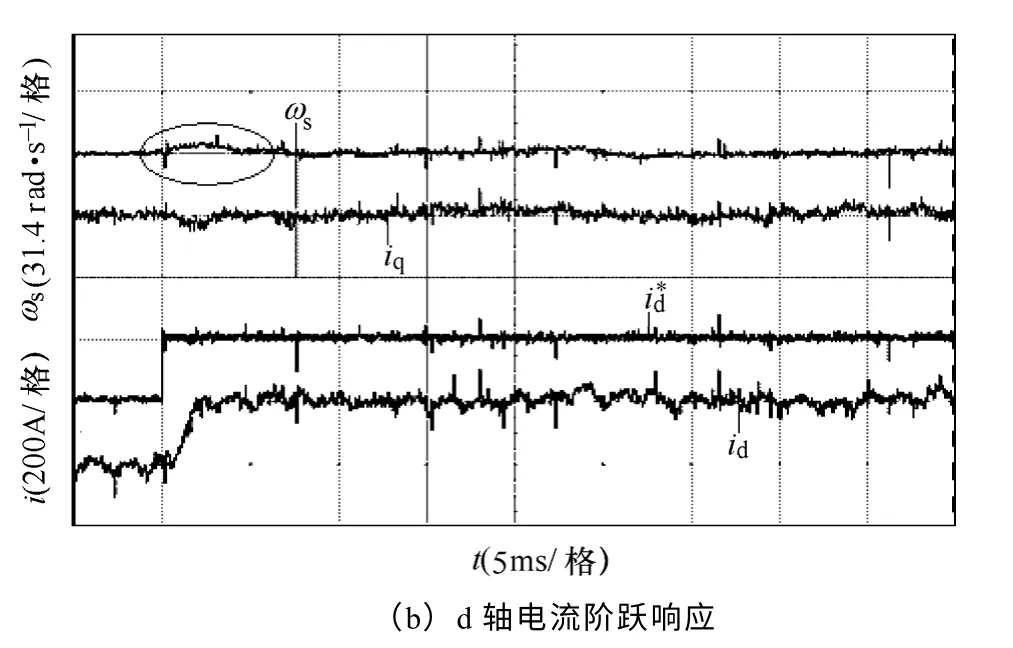
图15 电流阶跃响应瞬时转差角速度实验波形Fig.15 The experiment waveforms of instantaneous slip-angular speed with current step response

PWM 整流器采用如图6所提的基于VSFOC 策略，电流控制时引入前馈解耦环节。如图15a 和图 15b 所示，在d、q 轴电流阶跃响应动态过程中，瞬时转差角速度ωs明显小于ωg。稳态时ωs=0，d、q 轴之间的交叉耦合量为0。

综合以上的实验分析可知，相比于VAFOC 方式，VSFOC 方式可实现稳态完全解耦控制，同时可削弱动态过程的耦合，具有优异的电流响应特性，实验结果与理论分析相吻合。

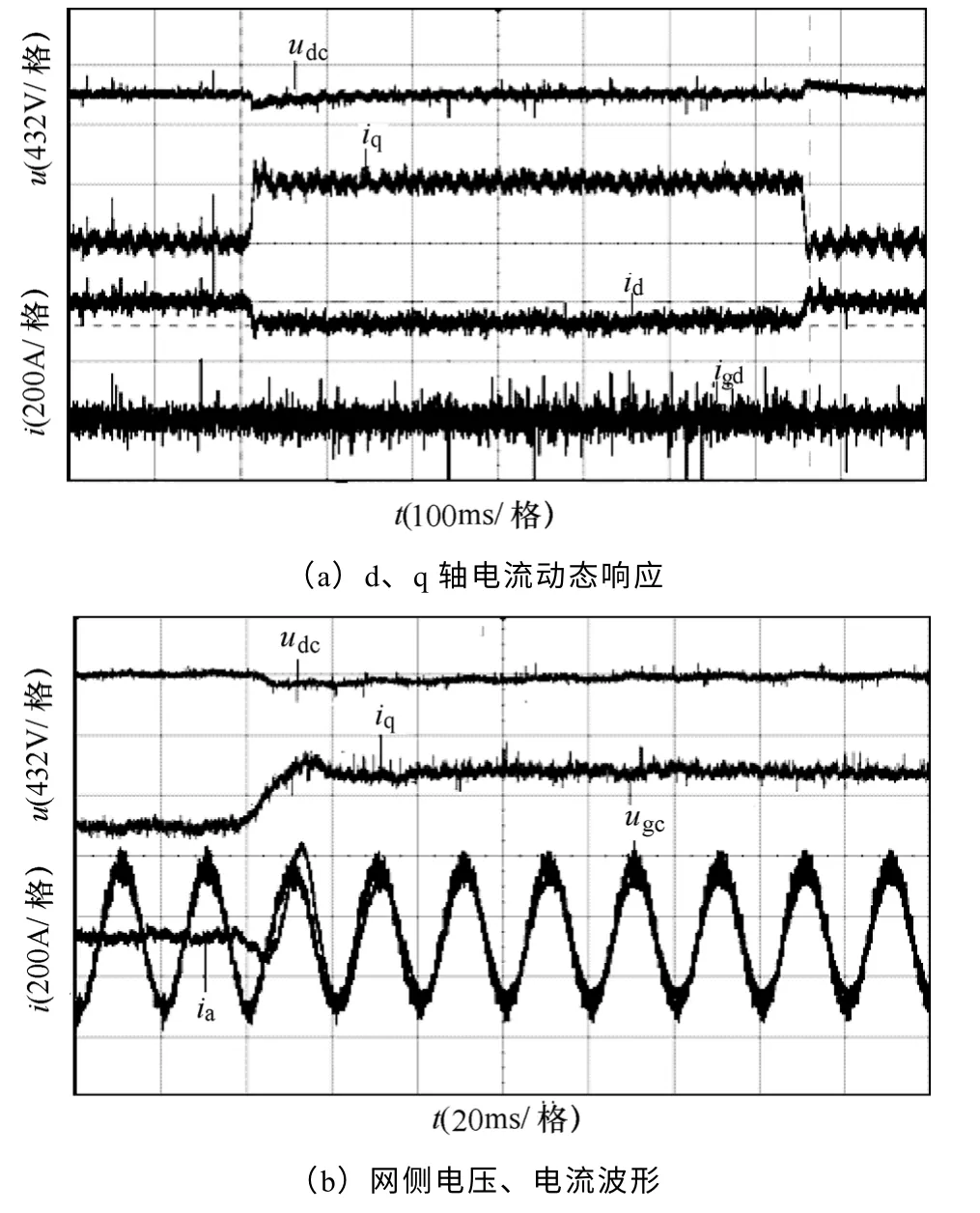
图16 功率馈入实验波形Fig.16 The experiment waveforms of power feed-in

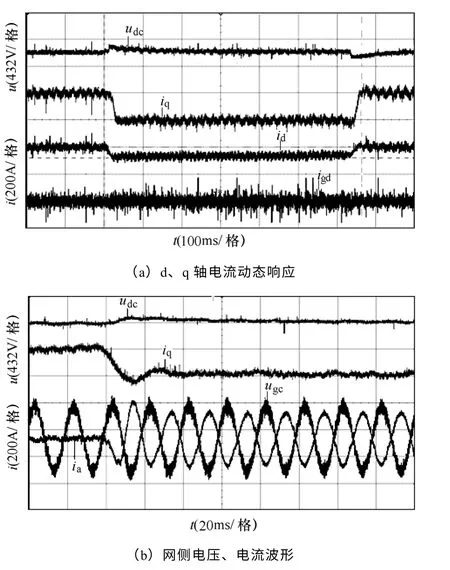
图17 功率馈出实验波形Fig.17 The experiment waveforms of power feed-out

图16和图17为采用本文所提的单位功率因数控制策略实验波形。从实验结果可以看出，采用VSFOC 方式，为满足系统单位功率因数运行，必须 调节出如图16a、图17a 所示的相应d 轴无功电流id。由图16b、图17b 网侧电压uga和电流ia可知，不论在功率馈入还是馈出工况下，采用所提控制方法均可实现网侧单位功率因数运行，电网侧电流正弦度良好，系统可满足四象限运行要求，验证了所提控制策略的有效性和优异的控制性能。

6 结论

本文引入三相电压型PWM 整流器“虚拟定子磁链”概念，提出了PWM 整流器最小耦合模型控制方法。围绕所提控制策略，建立了虚拟磁链定向方式下PWM 整流器数学模型，并与传统的虚拟电网磁链定向方式进行深入对比分析。提出了虚拟定子磁链定向下直接电流控制和功率因数控制，同时为保证控制策略的有效实施，构建了频率自适应虚拟定子磁链观测模型。实验结果分析得出以下结论。

（1）相比于传统的虚拟电网磁链定向方式，PWM 整流器采用虚拟定子磁链定向方式可实现稳态d、q 轴交叉耦合量为零，同时削弱动态过程交叉耦合影响。

（2）伴随着虚拟定子磁链的引入，d、q 轴交叉耦合量转换与瞬时转差角频率ωs相关，具有优异的电流响应特性，改善了动、静态控制性能。

（3）PWM 整流器采用虚拟定子磁链定向方式同样具有四象限运行特性，同时可实现电网侧单位功率因数运行，网侧电流正弦度良好。

（4）本文所提的虚拟定子磁链概念清晰，算法简单，便于系统设计和实现。

[1]Singh B,Singh B N,Chandra A,et al.A review of three-phase improved power quality AC-DC converters[J].IEEE Transactions on Industrial Electronics,2004,51(3):641-660.

[2]李时杰,李耀华,陈睿.背靠背变流系统中优化前馈控制策略的研究[J].中国电机工程学报,2006,26(22):74-79.

Li Shijie,Li Yaohua,Chen Rui.Study of the optimum feed-forward control strategy in back-to-back converter system[J].Proceedings of the CSEE,2006,26(22):74-79.

[3]谭国俊,吴轩钦,李浩,等.Back-to-Back 双三电平电励磁同步电机矢量控制系统[J].电工技术学报,2011,26(3):36-42.

Tan Guojun,Wu Xuanqin,Li Hao,et al.Study on vector control system of electrically excited synchro- nous motor fed by back-to-back dual three-level converter[J].Transactions of China Electrotechnical Society,2011,26(3):36-42.

[4]Buccella C,Cecati C,Latafat H.Digital control of power converters—a survey[J].IEEE Transactions on Industrial Informatics,2012,8(3):437-447.

[5]Dixon J W,Ooi B T.Indirect current control of a unity power factor sinusoidal current Boost type three- phase rectifier[J].IEEE Transactions on Power Electronics,1988,35(4):508-515.

[6]Kazmierkowski M P,Malesani L.Current control techniques for three-phase voltage-source PWM converters:a survey[J].IEEE Transactions on Industrial Electronics,1998,45(5):691-703.

[7]钟炎平,沈颂华.PWM 整流器的一种快速电流控制方法[J].中国电机工程学报,2005,25(12):52-56.

Zhong Yanping,Shen Songhua.A fast current control scheme for PWM rectifier[J].Proceedings of the CSEE,2005,25(12):52-56.

[8]赵仁德,贺益康,刘其辉.提高PWM 整流器抗负载扰动性能研究[J].电工技术学报,2004,19(8):67-72.

Zhao Rende,He Yikang,Liu Qihui.Research on improvement of anti-disturbance performance for three-phase PWM rectifiers[J].Transactions of China Electrotechnical Society,2004,19(8):67-72.

[9]赵仁德,贺益康.无电网电压传感器三相PWM 整流器虚拟电网磁链定向矢量控制研究[J].中国电机工程学报,2005,25(20):56-61.

Zhao Rende,He Yikang.Virtual line-flux-linkage oriented vector control of three-phase voltage source PWM rectifier without line voltage sensors[J].Proceedings of the CSEE,2005,25(20):56-61.

[10]吴凤江,汪之文,孙力.PWM 整流器的改进虚拟磁链定向矢量控制[J].电机与控制学报,2008,12(5):504-508.

Wu Fengjiang,Wang Zhiwen,Sun Li.Improved virtual flux oriented vector control of PWM rectifier[J].Electric Machines and Control,2008,12(5):504-508.

[11]Tan Guojun,Wu Xuanqin,Zhao Yanping,et al.Study on sensorless control strategy of multi-level PWM rectifier based on a novel virtual flux observer[C].Proceedings of the Asia-Pacific Power and Energy Engineering Conference,2010:1-4.

[12]Hadian A S R,徐殿国,郎永强.一种PWM 整流器直接功率控制方法[J].中国电机工程学报,2007,27(25):78-84.

Hadian A S R,Xu Dianguo,Lang Yongqiang.A new direct powercontrol of PWM rectifier[J].Proceedings of the CSEE,2007,27(25):78-84.

[13]王久和,李华德,王立明.电压 PWM 整流器直接功率控制系统[J].中国电机工程学报,2006,26(18):54-60.

Wang Jiuhe,Li Huade,Wang Liming.Direct power control systemof three phase Boost type PWM rectifiers[J].Proceedings of the CSEE,2006,26(18):54-60.

[14]Malinowski M,Jasin’ski M,Kazmierkowski M P.Simple direct power control of three-phase PWM rectifier using space-vector modulation(DPC-SVM)[J]. IEEE Transactions on Industrial Electronics,2004,51(2):447-454.

[15]杨兴武,姜建国.电压型PWM 整流器预测直接功率控制[J].中国电机工程学报,2011,31(3):34-39.

Yang Xingwu,Jiang Jianguo.Predictive direct powercontrol for three-phase voltage source PWM rectifiers[J].Proceedings of the CSEE,2011,31(3):34-39.

[16]尚磊,孙丹,胡家兵,等.三相电压型并网逆变器预测直接功率控制[J].电工技术学报,2011,26(7):216-226,229.

Shang Lei,Sun Dan,Hu Jiabing,et al.Predictive direct power control of three-phase grid-connected voltage-sourced inverters[J].Transactions of China Electrotechnical Society,2011,26(7):216-226,229.

[17]Kouro S,Cortes P,Vargas R,et al.Model predictive control—a simple and powerful method to control power converters[J].IEEE Transactions on Industrial Electronics,2009,56(6):1826-1838.

[18]张平化,杨贵杰,李铁才.三相 PWM 整流器的反馈线性化直接电压控制[J].中国电机工程学报,2010,30(18):39-46.

Zhang Pinghua,Yang Guijie,Li Tiecai.Direct voltage control of three-phase PWM rectifier based on feedback linearization[J].Proceedings of the CSEE,2010,30(18):39-46.

[19]邓卫华,张波,丘东元,等.三相电压型PWM 整流器状态反馈精确线性化解耦控制研究[J].中国电机工程学报,2005,25(7):97-103.

Deng Weihua,Zhang Bo,Qiu Dongyuan,et al.The research of decoupled state variable feedback linearization control method of three-phase voltage source PWM rectifier[J].Proceedings of the CSEE,2005,25(7):97-103.

[20]周鑫,郭源博,张晓华,等.基于自适应跟踪控制的三相电压型 PWM 整流器[J].中国电机工程学报,2010,30(27):76-82.

Zhou Xin,Guo Yuanbo,Zhang Xiaohua,et al.Three-phase voltage-type PWM rectifier based on adaptive tracking control[J].Proceedings of the CSEE,2010,30(27):76-82.

[21]Sato Y,Ishizuka T,Nezu K,et al.A new control strategy forvoltage-type PWM rectifiers to realize zero steady-state control errorin input current[J].IEEE Transactions on Industry Applications,1998,34(3):480-486.

[22]Malinowski M,Kazmierkowski M P,Trzynadlowski A M.A comparative study of control techniques for PWM rectifiers in AC adjustable speed drives[J].IEEE Transactions on Power Electronics,2003,18(6):1390-1396.