单相电压型全桥逆变器的反步滑模控制策略

侯 波 穆安乐 董锋斌 刘俊伟 刘宏昭

（1.西安理工大学机械与精密仪器工程学院 西安 710048 2.陕西理工学院电气工程学院 汉中 723003）

0 引言

逆变器作为一种典型的电力电子装置，已被广泛应用于交流传动、有源滤波、光伏发电和风力发电等国民经济中的各行各业[1-3]，成为生产生活中不可缺少的关键设备。电力电子装置是一类典型的开关型非线性系统，传统的线性控制方法应用于该类系统时，其快速性和精确性不能达到理想要求。因而，现代非线性控制方法在电力电子系统中的应用已成为当前电力电子控制的研究热点之一[4-6]。目前逆变器控制应用方案主要有双闭环控制、无差拍控制和重复控制等，虽然都对逆变器的性能有所提高，但也存在不同程度的问题[7]。随着对非线性控制理论的深入研究，基于微分几何理论的精确线性化方法在逆变器中得到了广泛的应用[7-12]，然而该方法建立在被控对象具有精确数学模型的基础上，未考虑实际系统不确定性问题，因而鲁棒性不强，计算表达式复杂，工程实现较为困难。反馈无源化方法从系统能量角度出发，通过保持系统的无源性，使得系统内部稳定。文献[13]采用反馈无源化方法设计了三相光伏并网逆变器的电流控制器，仿真和实验验证了其有效性，但反馈无源化方法要求系统相对阶为1，限制了反馈无源化方法在逆变器中的应用范围。H∞控制在抗干扰能力方面的性能优越，文献[14]基于H∞控制理论设计了单相电压型逆变器的H∞输出反馈控制器，但设计过程需要求解 HJD（Hamilton-Jaccohi-Issaes）不等式，目前对于 HJD不等式没有一般的求解方法，获得准确数值解十分困难，往往需要反复试凑和一定的设计经验。由上述分析可知，目前提出的各种主流非线性控制方法在电力电子中的应用并不十分完善，依然有许多问题尚待解决。

1991年，美国控制学教授Kokotovic 提出了一种全新的非线性控制方法即反步法，该方法由于设计过程简明，易为工程人员接受，在许多领域中得到了广泛的应用[15]。文献[16,17]采用反步法分别提出了三相电压型脉冲宽度调制逆变器和三相四桥臂逆变器的非线性反馈控制器，所提方法的控制性能明显优于传统的PI 控制，但在实际应用中却存在以下问题：①逆变器数学模型均建立在精确模型基础上，未考虑实际系统中存在的不确定性问题；②未考虑外界干扰对控制性能的影响。上述两个问题限制了反步法在逆变器中的应用。滑模变结构的滑动模态具有不变性，对系统数学模型依赖程度低，对于系统参数摄动以及外界干扰具有很强的鲁棒性[18]，从而在逆变器这类具有开关特性的系统中得到了大量的应用[19]。文献[20]将反步法和滑模控制相结合，利用滑模控制强鲁棒性弥补反步法缺陷，提高控制器对系统参数不确定性以及外扰的鲁棒性。文献[21]采用反步滑模控制分别设计了交流异步电机机械部分和电气部分非线性控制器，实现了系统快速的速度、转矩和磁链的渐近跟踪。文献[22]以扩张观测器、积分滑模控制和反步法相结合的方式设计了电机驱动系统非线性控制器，有效地提高了系统的动、静态性能。上述研究结果表明，反步滑模控制能够有效地减少反步法对控制对象精确建模的依赖性，然而关于此方法在通用电压型逆变器的应用研究却未见文献报道。

基于上述原因，本文提出了一种适于单相电压型全桥逆变器的反步滑模控制策略。首先采用状态空间平均法建立了单相全桥逆变器的连续数学模型。在此基础上，以逆变器的输出滤波电容电压及其导数为状态变量，建立了符合反步设计所需的严参数反馈形式的非线性数学模型，同时建立了相应的非精确数学模型。其次在反步设计的最后一步，利用滑模变结构方法，选取滑模面及指数趋近律，设计了系统的反步滑模反馈控制律。采用本文提出的反步滑模控制方法，利于通过反步法建立滑模面，利用滑模控制可有效地提高逆变器系统的鲁棒性，改善系统的稳态和动态性能。最后通过实验验证了控制方案的有效性和合理性。

1 单相电压型全桥逆变器数学模型

单相全桥逆变器主拓扑结构如图1所示。

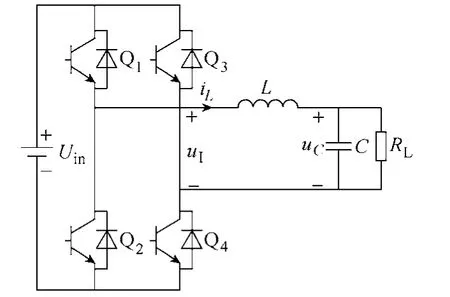
图1 单相电压型全桥逆变器电路拓扑Fig.1 Circuit diagram of the single-phase voltage source full-bridge inverter

逆变器包括电压源Uin、四个功率开关管Q1～Q4、电感L、电容C以及等效负载RL。其中，电感L电流为iL，电容C电压为uC。假设图1中的开关为理想开关，忽略开关的死区时间以及电感L和电容C的寄生电阻。依据基尔霍夫电压、电流定律可得到

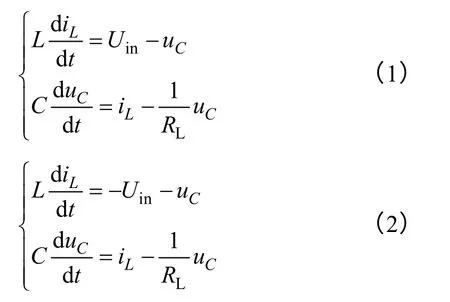
式（1）、式（2）分别对应于Q1和Q4导通时、Q2和Q3导通时。

采用状态空间平均法[23]，可得到单相全桥逆变器的连续数学模型

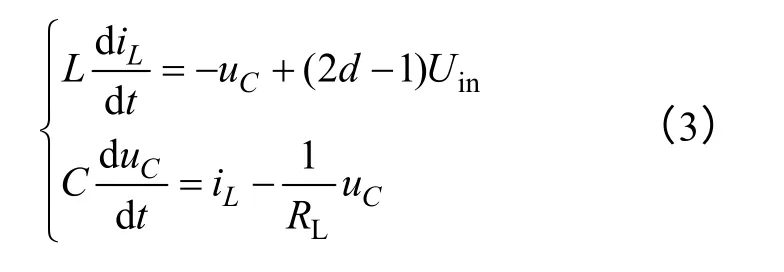
式中，d为Q1和Q4的占空比，0≤d≤1。

为了将式（3）转换为符合反步设计所需的严参数反馈形式，可作如下变换

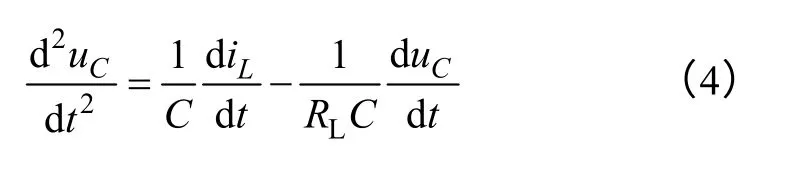
将式（3）代入式（4），并进行整理可得

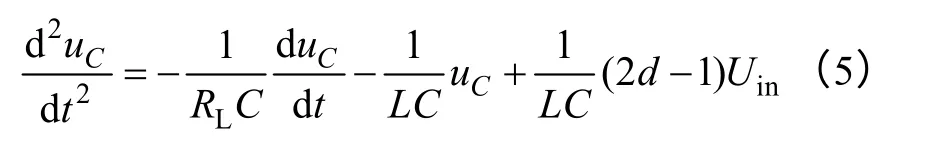
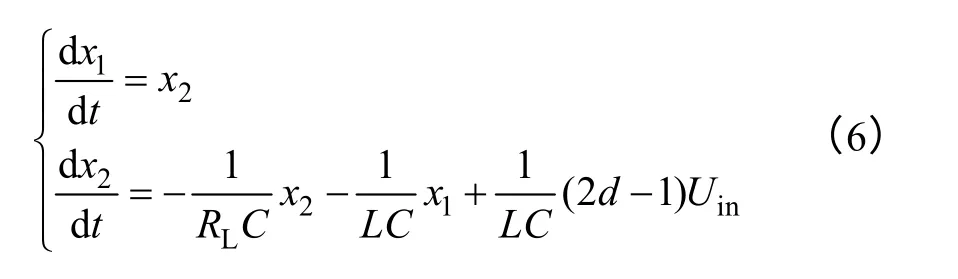
对于全桥电压型逆变器的输出滤波电容电压及其导数是可以连续测量的，式（6）完全符合实际情况。由式（6）知，其符合反步设计所需的严参数反馈形式[15]。

逆变器中存在诸多的不确定因素，如滤波电感、电容实际参数与理论参数存在偏差，滤波电感、电容的等效电阻无法精确测量，系统运行过程中滤波电感、电容的老化和负载具有时变性等。考虑到上述诸多不确定因素，式（6）重写为

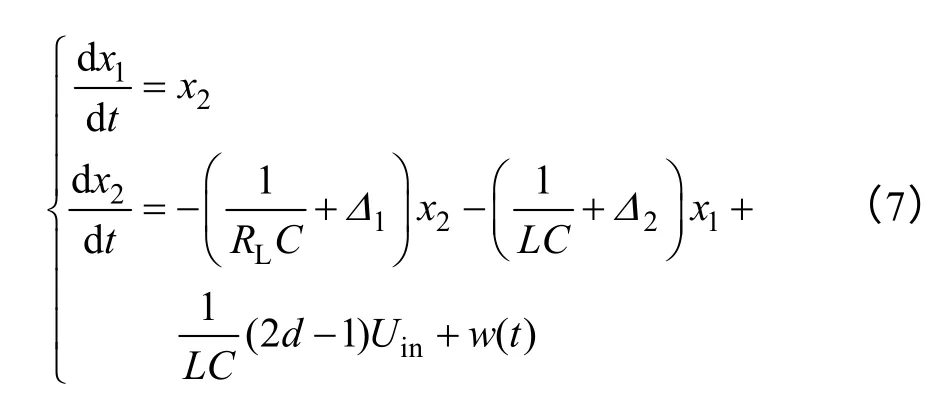
式中，1Δ和2Δ为系统参数不确定性部分；w(t)为外界干扰。令不确定项和外界干扰的总不确定性为

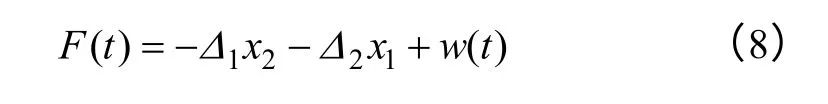
式（8）包含了逆变器中存在的所有不确定性、外部扰动等所有摄动，由式（7）和式（8）可得单相全桥逆变器的非精确数学模型为

2 单相电压型全桥逆变器反步滑模控制律

在反步法设计之前，首先需要定义跟踪误差。单相桥式逆变器控制目标为输出电压跟踪预先给定的参考电压，因此选取跟踪误差z1为电容电压uC与参考电压xd之差。

反步法将满足严参数反馈形式的非线性系统分解为不超过系统阶数的子系统，并对每个子系统设计Lyapunov 函数和中间虚拟控制量，直到“后退”到整个系统。由式（9）可知，其为二阶系统，因此系统反步设计分为两个步骤。

（1）选取Lyapunov 函数为

对式（11）求导，并结合式（10）得

取x1子系统的虚拟控制量z2为

式中，c1为可调整的控制参数，c1＞0。

由式（13）可得

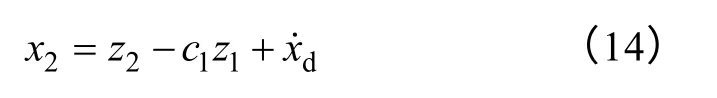
将式（14）代入式（12）得

（2）选取Lyapunov 函数V2为

对V2求导数，得

由式（13）并结合式（9）得到

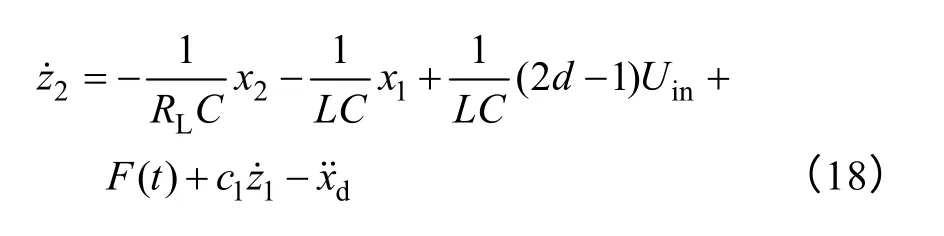
将式（18）代入式（17）得到

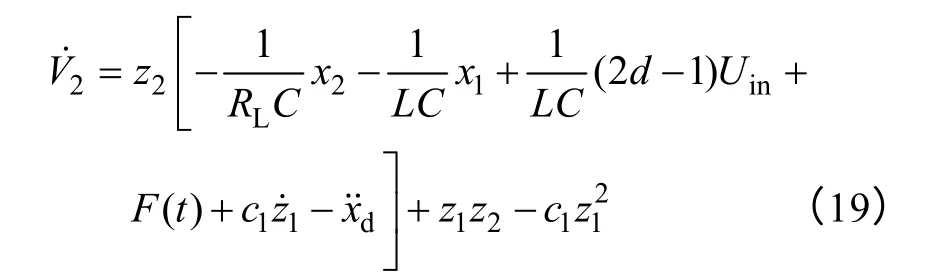
虚拟控制量z2由式（10）中的两个误差信号组成。依据滑模控制理论[24]，选择滑模面

滑模趋近律选为

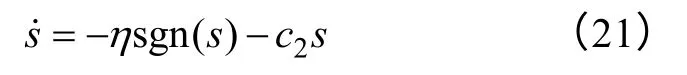
式中，η＞0，c2＞0。

利用式（20）、式（21）并结合式（19），可设计如下的控制律

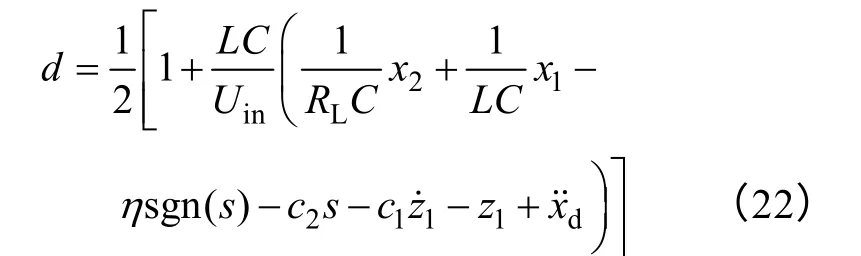
将式（22）代入式（19）得

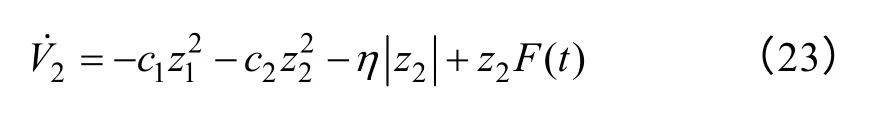
式中，存在不确定项F(t)，难以通过式（23）判别系统的稳定性。根据单相电压型逆变器的工作原理，在一个开关周期内逆变器电容电压、电感电流和直流供电电压波动有限，根据式（8），F(t)是有限的，设|F(t)|≤K，K为F(t)的上限。选取控制参数η≥K，由式（23）可得

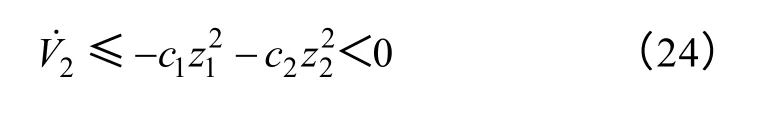
根据Lyapunov 稳定性定理，由式（24）和式（16）得闭环系统在(z1,z2)=（0,0）处是渐近稳定的，即当t→∞时，有z1→0 和z2→0。再由式（10）和式（13）得式（9）、式（22）所构成的闭环系统在（dx,dx˙）是渐近稳定的，从而实现了对参考信号xd和dx˙的跟踪控制。

为避免滑模控制中存在的“抖振”现象，本文使用式（25）函数代替式（22）中sgn(s)。

式中

综上所述，可得如图2所示的单相电压型全桥逆变器的非线性控制。

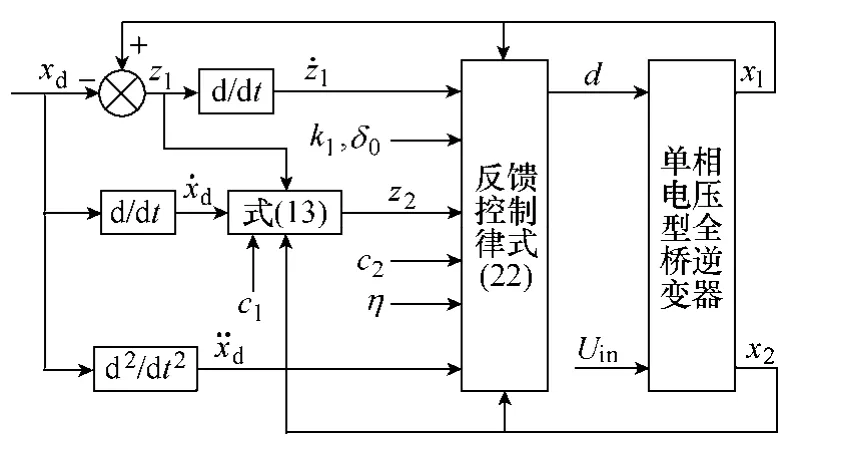
图2 单相电压型全桥逆变器非线性控制Fig.2 Nonlinear control graph of the single-phase voltage source full-bridge inverter

3 实验结果

为验证本文给出的控制策略的有效性，利用PSIM 对系统进行了仿真，同时搭建了相应的实验平台，控制算法是基于TMS320F2812DSP 实现的。系统参数分别为输入直流电压Uin=450V，输出50Hz交流电压的有效值为220V，额定负载RL=44Ω，输出LC 滤波器标定参数为L=6.4mH、C=25μF。LC参数摄动范围为L=5～7.5mH、C=22～28.2μF，反馈控制律参数选取为c1=1×106、c2=6 000、η=1×109、δ0=46 和k1=100。

在纯阻性额定负载情况下进行了仿真和实验验证，直流母线电压选取450V。图3a 为L=5mH、C=28.2μF时负载电压和负载电流仿真波形；图3b为L=6.4mH、C=25μF时实验波形，电压THD 为1.78%；图3c 为L=5mH、C=28.2μF时实验波形，电压THD 为1.93%。对其他滤波参数组合进行了实验测试，测试结果为L=5mH、C=22μF时，电压THD为2.1%；L=7.5mH、C=28.2μF时，电压THD 为1.84%。上述结果表明，本文所提控制策略对于逆变器LC 滤波参数变化不敏感，输出电压稳态误差和畸变小，能够保证输出电压准确、快速地跟踪参考信号。

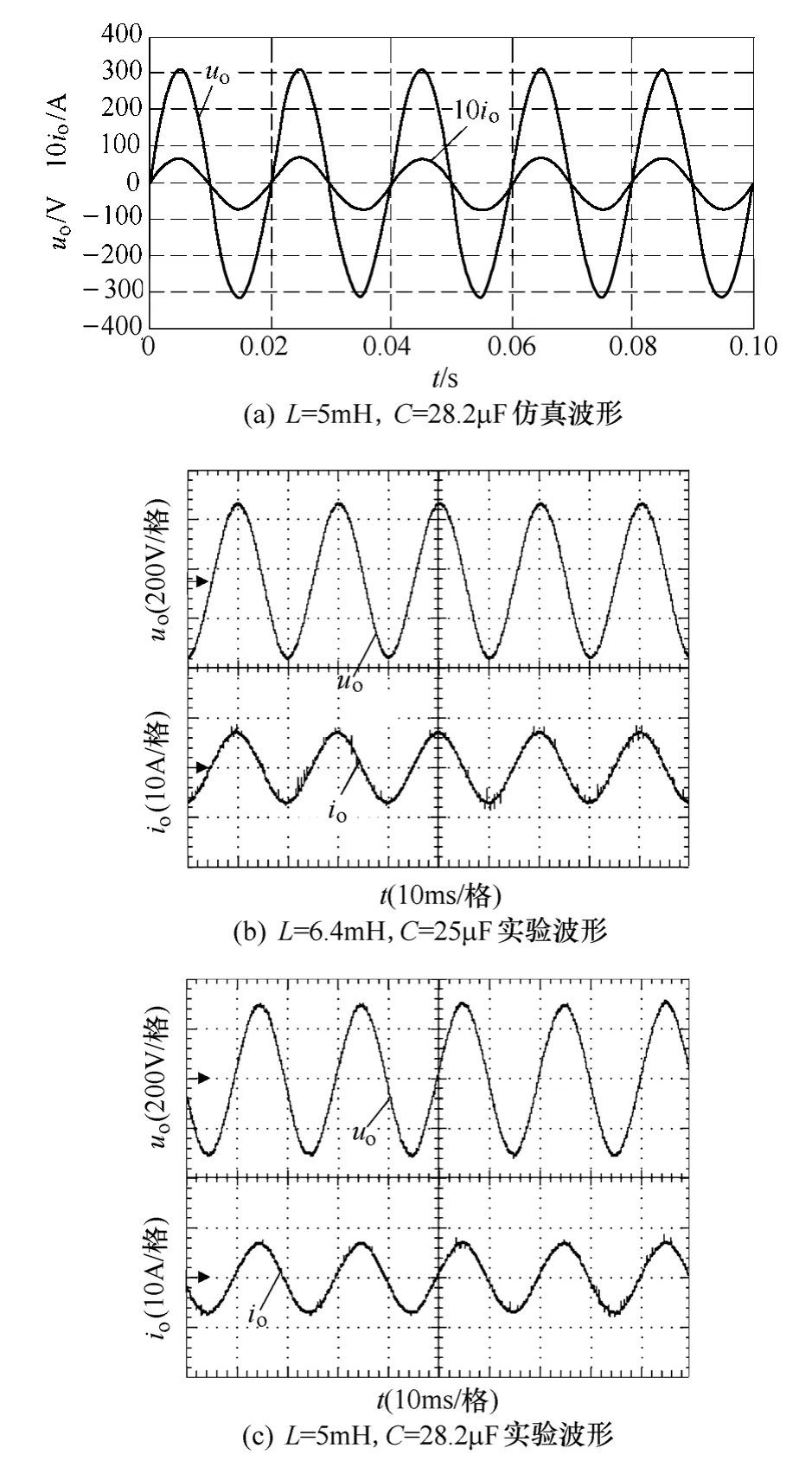
图3 改变LC 滤波参数时仿真和实验波形Fig.3 The simulation and experiment waveforms while changing the LC filter parameters

对逆变器负载抗扰动能力进行了实验验证。实验中LC 滤波参数选取为L=5mH、C=28.2μF，负载电压、电流以及逆变桥输出电压uI实测波形如图4所示。由图4可知，突加额定负载时，系统暂态过渡时间大约2ms，电流波形平滑地过渡到稳定状态，表明本文所提控制策略具有快速的动态特性，对负载电流具有良好的抗扰动能力。

非线性负载采用典型的单相桥式不可控整流电路，LC滤波参数选用标称值，整流器滤波电容为1 500μF，负载电阻为100Ω，图5为逆变器非线性负载时的实测波形。由图5知，在非线性负载情况下电压波形畸变小，输出电压THD为2.58%，完全满足国际标准IEEE 519—1992中关于THD小于5%的 要求。

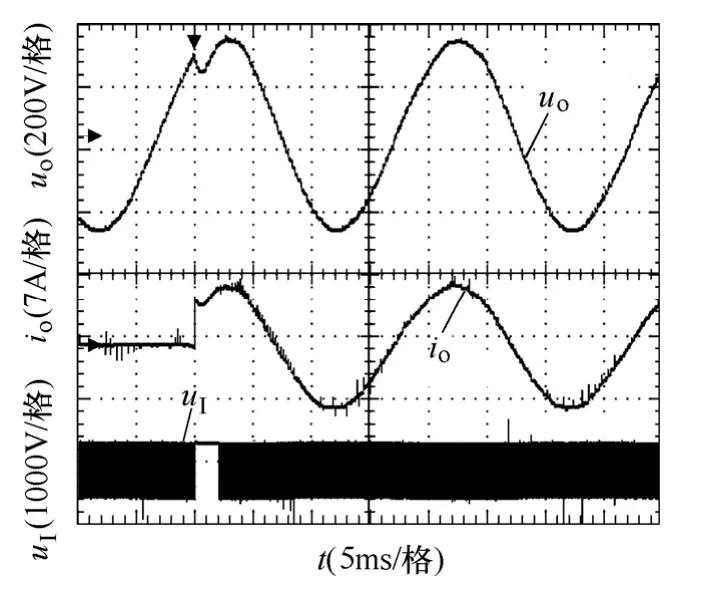
图4 突加额定负载时实验波形Fig.4 The experiment waveforms while increasing rated load

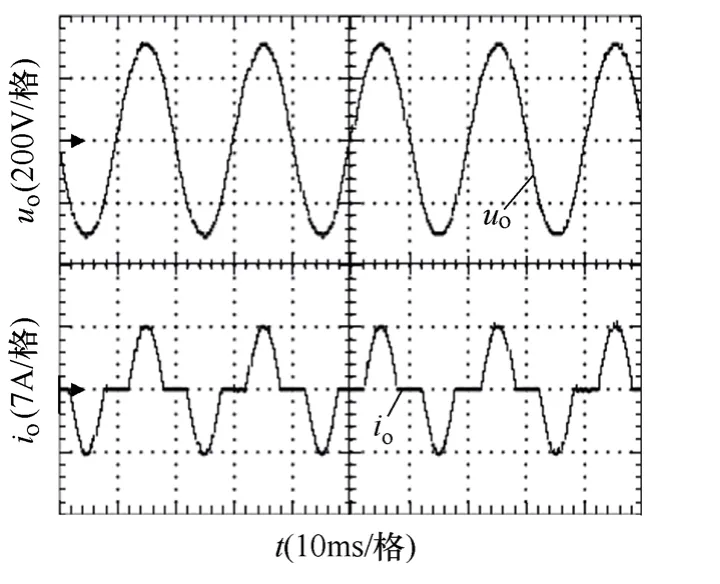
图5 整流型负载时电压和电流波形Fig.5 Voltage and current waveforms of rectifier load

将单相全桥逆变器的输入直流母线电压分别设定为420V、480V 和450V，LC 滤波参数选用标称值、额定负载时的负载电压和电流分别如图6和图3b 所示，输出电压THD分别为1.25%、1.98%和1.78%。

上述实验结果表明，负载电压和电流基本不受输入直流电压的影响，说明本文的控制方法对逆变器输入直流母线电压具有前馈作用，这是由于式（22）中含有前馈项Uin。

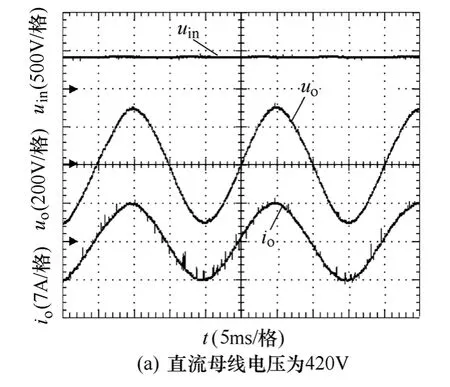
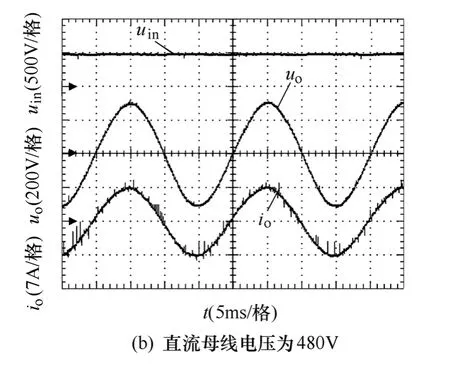
图6 直流母线电压扰动实验波形Fig.6 The experiment waveforms while DC voltage disturbing

4 结论

在单相电压型全桥逆变器主电路拓扑结构基础上，以输出电容电压及其导数为状态变量，建立了具有严参数反馈形式的二阶单输入、单输出的单相电压型全桥逆变器数学模型。在此基础上，将反步法和滑模控制相结合，推导出具有参数不确定和外界干扰情况下的单相电压型全桥逆变器的反馈控制律。实验结果表明，本文的控制策略具有良好的稳态和动态性能，不仅能够适于线性和非线性负载，而且更接近工程应用实际。提出的单相电压型全桥逆变器反步滑模控制策略可推广到其他不同类型的逆变器中，为逆变器控制系统设计提供了一种思路。所提控制策略结构简单，采用普通的微处理器即可实现，因而具有良好的工程应用前景。

[1]顾和荣,王德玉,沈虹,等.三相四桥臂逆变器控制技术研究[J].电力系统保护与控制,2011,39(24):41-46.

Gu Herong,Wang Deyu,Shen Hong,et al.Research on control scheme of three-phase four-leg inverter[J].Power System Protection and Control,2011,39(24):41-46.

[2]姚致清,张茜,刘喜梅.基于PSCAD/EMTDC 的三相光伏并网发电系统仿真研究[J].电力系统保护与控制,2010,38(17):76-81.

Yao Zhiqing,Zhang Qian,Liu Ximei.Research on simulation of a three-phase grid-connected photovoltaic generation system based on PSCAD/EMTDC[J].Power System Protection and Control,2010,38(17):76-81.

[3]赵梅花,阮毅,杨勇,等.直驱式混合励磁风力发电系统控制策略的研究[J].电力系统保护与控制,2010,38(12):19-23.

Zhao Meihua,Ruan Yi,Yang Yong,et al.Control strategy study on direct-driven type hybrid excitation wind power system[J].Power System Protection and Control,2010,38(12):19-23.

[4]张平化,杨贵杰,李铁才.三相 PWM 整流器的反馈线性化直接电压控制[J].中国电机工程学报,2010,30(18):39-46.

Zhang Pinghua,Yang Guijie,Li Tiecai.Direct voltage control of three phase PWM rectifier based on feedback linearization[J].Proceedings of the CSEE,2010,30(18):39-46.

[5]王久和.电压型PWM 整流器的非线性控制[M].北京:机械工业出版社,2008.

[6]Gensior A,Sira-Ramirez H,Rudolph J,et al.On some nonlinear current controllers for three-phase boost rectifiers[J].IEEE Transactions on Industrial Electronics,2009,56(2):360-370.

[7]姚玮,陈敏,牟善科,等.基于反馈线性化的高性能逆变器数字控制方法[J].中国电机工程学报,2010,30(12):14-19.

Yao Wei,Chen Min,Mou Shanke,et al.Digital control method for high-performance inverters based on feedback linearization[J].Proceedings of the CSEE,2010,30(12):14-19.

[8]石峰,查晓明.应用微分几何理论的三相并联型有源电力滤波器解耦控制[J].中国电机工程学报,2008,28(15):92-97.

Shi Feng,Zha Xiaoming.Decoupled control of the shunt three-phase active power filter applying differential geometry theory[J].Proceedings of the CSEE,2008,28(15):92-97.

[9]张兴,张崇巍,曹仁贤.光伏并网逆变器非线性控制策略的研究[J].太阳能学报,2002,23(6):770-773.

Zhang Xing,Zhang Chongwei,Cao Renxian.Study on nonlinear control of FV parallel feed inverter[J].Acta Energiae Solaris Sinica,2002,23(6):770-773.

[10]陈艳,周林,雷建,等.基于微分几何的微网Z 源逆变器并网控制[J].电工技术学报,2012,27(1):17-23.

Chen Yan,Zhou Lin,Lei Jian,et al.Research on the Z-source inverter grid-connected control of micro- grid system based on differential geometry[J].Transactions of China Electrotechnical Society,2012,27(1):17-23.

[11]董锋斌,钟彦儒.基于状态反馈精确线性化的三相四桥臂逆变器的控制[J].信息与控制,2012,41(5):544-552.

Dong Fengbin,Zhong Yanru.Control of three-phase four-leg inverter by sate feedback exact linearization[J].Information and Control,2012,41(5):544-552.

[12]帅定新,谢运祥,杨金明,等.基于状态反馈精确线性化单相全桥逆变器的最优控制[J].电工技术学报,2009,24(11):120-126.

Shuai Dingxin,Xie Yunxiang,Yang Jinmin,et al.Optimal control of single-phase full-bridge inverters by state feedback linearization[J].Transactions of China Electrotechnical Society,2009,24(11):120-126.

[13]王久和,慕小斌.基于无源性的光伏并网逆变器电流控制[J].电工技术学报,2012,27(11):176-182.

Wang Jiuhe,Mu Xiaobin.Current control strategy of photovoltaic grid-connected inverter based on passivity[J].Transactions of China Electrotechnical Society,2012,27(11):176-182.

[14]陈宝远,邹丽爽,吴茜,等.基于H∞控制算法的单相逆变电源控制器研究[J].哈尔滨理工大学学报,2010,15(4):14-18.

Chen Baoyuan,Zou Lishuang,Wu Qian,et al.Study on single-phase inverter controller based onH∞control algorithm[J].Journal of Harbin Universigy of Science and Technology,2010,15(4):14-18.

[15]胡跃明.非线性控制理论与应用[M].北京:国防工业出版社,2005.

[16]董锋斌,钟彦儒.反步法在三相电压型脉冲调宽逆变器控制中的应用[J].控制理论与应用,2012,29(7):928-932.

Dong Fengbin,Zhong Yanru.Control of three-phase voltage pulse-width-modulation inverters by back- stepping design approach[J].Control Theory & Applications,2012,29(7):928-932.

[17]董锋斌,钟彦儒.反向递推法在三相四桥臂逆变器 控制中的应用[J].电机与控制学报,2012,16(4):30-35.

Dong Fengbin,Zhong Yanru.Application of backstepping for three-phase four-leg inverter[J].Electric Machine and Control,2012,16(4):30-35.

[18]高为炳.变结构控制的理论及设计方法[M].北京:科学出版社,1996.

[19]张黎,丘水生.滑模控制逆变器的分析与实验研 究[J].中国电机工程学报,2006,26(3):59-63.

Zhang Li,Qiu Shuisheng.Analysis and experimental study of sliding mode control inverter[J].Proceedings of the CSEE,2006,26(3):59-63.

[20]Hsin-Jang S,Kuo-Kai S.Nonlinear slidingmode torque control with adaptive backstepping approach for induction motor drive[J].IEEE Transactions on Industrial Electronics,1999,46(2):380-389.

[21]王家军,王建中,马国进.感应电动机系统的变结构反推控制研究[J].中国电机工程学报,2007,27(6):35-38.

Wand Jiajun,Wang Jianzhong,Ma Guojin.Variable structure control with backstepping of induction motor system[J].Proceedings of the CSEE,2007,27(6):35-38.

[22]王礼鹏,张化光,刘秀翀,等.基于扩张状态器的SPMSM 调速系统的滑模变结构反步控制[J].控制与决策,2011,26(4):553-557.

Wand Lipeng,Zhang Huaguang,Liu Xiuchong,et al.Backstepping controller based on sliding mode variable structure for speed control of SPMSM with extended state observer[J].Control and Decision,2011,26(4):553-557.

[23]徐德鸿.电力电子系统建模及控制[M].北京:机械工业出版社,2006.

[24]Khalil H K.Nonlinear systems[M].New Jersey:

Pearson Education,2002.