用场路耦合模拟变压器线圈部分短路故障电流的方法

张俊杰 刘兰荣 刘东升 刘力强 张喜乐 胡启凡

（保定天威保变电气股份有限公司电工技术研究所 保定 071056）

0 引言

大型电力变压器故障状态和暂态过程复杂[1]，属于瞬态问题，解析计算复杂。但为了找出故障起因（是先变压器内部故障还是先外围故障），推导故障的演变，判断故障位置（内部线圈情况如何），以便认清责任、总结教训，避免以后类似事故的再发生，需要对短短ms 级的故障动态过程做详细的分析[2,3]。三维场路耦合（field-circuit coupling）有限元（Finite Element Method，FEM）方法使很多复杂的电磁问题得以简化，并能够得到较准确的解[4-6]，而且伴随着计算机技术的迅速提高，得到了广泛的应用。场路耦合法可自动计算故障匝数线圈内的感生电流以及对一次绕组漏感变化，直观地给出各绕组稳态参数，获得故障状态下的线端短路稳态电流。若再根据故障时刻初相角和系统参数，通过数学模型模拟短路发生后的故障波形，与实际故障波形对比，便可以判断发生该短路故障的可能性，并可验证发生短路的起始位置。

本文以模拟某台500kV 单相自耦变压器高压侧实际短路故障为例，介绍这种方法的实现过程。

1 系统等效电路

一次侧短路时刻系统等效电路如图1所示。

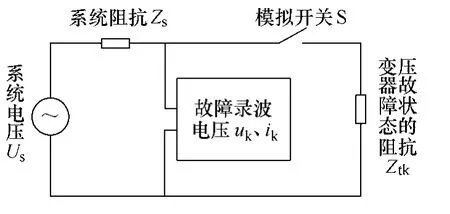
图1 分析短路电流的一次侧系统等效电路Fig.1 The schematic circuit when the transformer was faulted

交流电压源us(t)=Ussin(ωt+α)，假定t=0时，模拟突然短路的开关S闭合，短路电流的波形为[7]

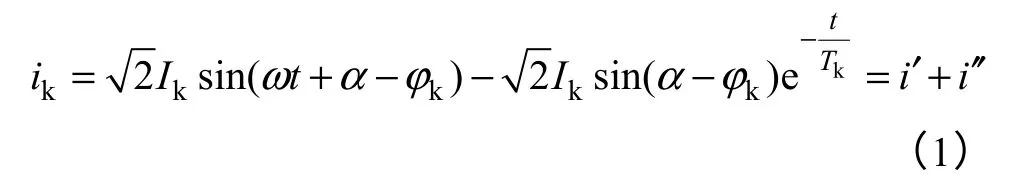
1.1 系统阻抗Zs计算

系统阻抗Zs与系统不同有关，若同一系统与其不同的运行方式有关，为了统一计算国家标准GB 1094.5 给出系统阻抗[8]。根据国家标准GB 1094.5对于电压等级为500kV 的变压器，给定500kV 系统的短路视在容量S=60 000MV⋅A，则系统线路阻抗为

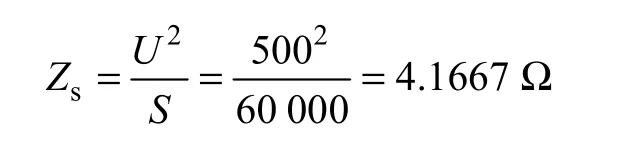
近似计算可以认为该阻抗是感性的，具体的推算如下：

按GB 1094.5 双绕组变压器短路试验的第一个峰值（kA）为

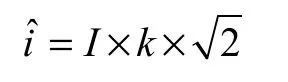
式中，I是对称短路电流；是峰值因数，与线路的X/R有关，而标准对Ⅲ类变压器（容量＞100 000kV ⋅A 以上）的峰值因数取为

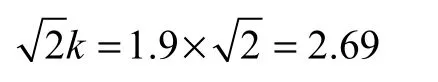
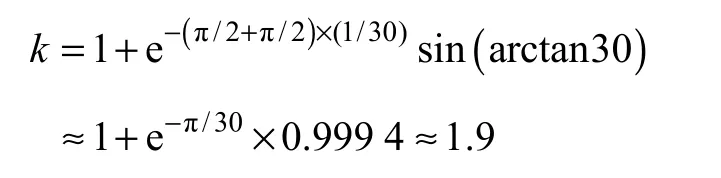
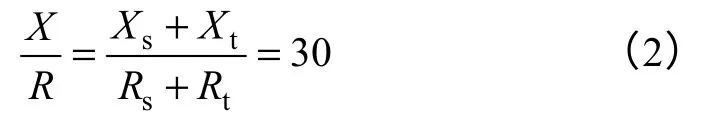
变压器正常运行状态下的短路阻抗Zt的有功分量Rt由线圈直流电阻计算得到，而无功分量Xt由阻抗电压计算得到。且有

已知Zs、Rt和Xt，代入式（2）和式（3），可以得到线路阻抗Zs的有功和无功分量

1.2 变压器故障状态下的短路阻抗Ztk计算

一个高压线圈假设有部分线匝短路，可认为短路故障线匝构成第2 个线圈，建立独立的局部短路的线圈，如图2所示sx 绕组。

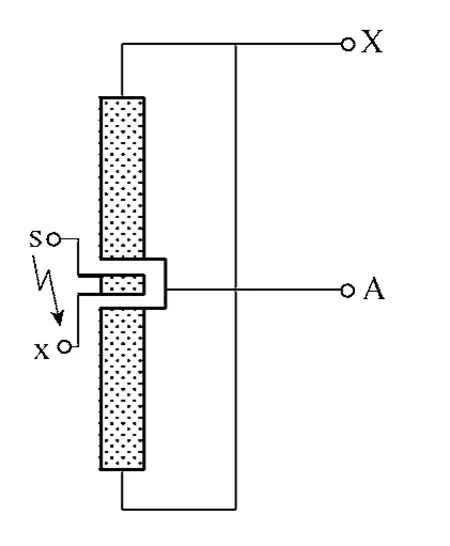
图2 一个高压线圈有短路匝的电路示意Fig.2 The schematic circuit when a local short circuit was happened in the high voltage winding

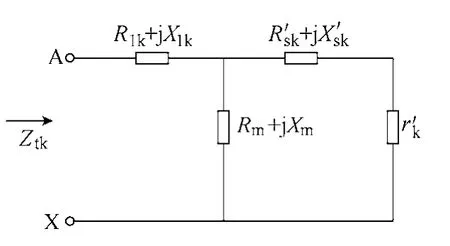
图3 单绕组有故障匝的等效电路Fig.3 The equivalent circuit when a local short circuit was happened

由于短路发生时刻变压器运行状态不尽相同，或空载运行或负载运行，加上短路时变压器自身的直流电阻和电抗都发生了复杂的变化，如果用等效电路（多个绕组形成等效网络）计算，各个线圈直流电阻需要折算到一次侧，一次电抗的计算更为复杂。

如果采用图2的线圈布置，直接计算场路耦合磁场，故障状态下的一次电抗可以方便地用能量法、磁链法或欧姆法得到。若采用欧姆法（电压和电流向量相除）还可以直接得出故障状态下变压器的短路阻抗Ztk的有功分量Rtk和无功分量Xtk。本文便是据此讨论该方法的实现过程。

1.3 故障点接触电阻rk计算

该电阻是短路导线通过短路电流熔化的原因，接触电阻是随机的，取决于短路点的接触情况，可能范围在100～10 000 μΩ，该值与短路点的发热有 关，计算中取值为1000 μΩ。

2 建模

2.1 假设条件

（1）变压器故障前后单相变压器分接状态、联结组标号、空载或负载等状态没有变化，建模时将模型电路按实际连接状态接好。

（2）因要计算故障后的稳态电流，短路故障后一次侧电网电压不变，系统接入正弦电压源。

（3）一个高压线圈假设有部分线匝短路，所占线圈高度按短路的实际线匝高度给定，建立独立的局部短路的故障线圈。

2.2 绕组直流电阻的影响

建模定义绕组时，线圈的横截面一般是按线圈的电抗高度和宽度建立的，线圈的油道、绝缘都已包含在内。一般在电磁软件设定为多股线圈类型，实际计算中绕组直阻由每匝面积决定。默认的每匝面积计算式为

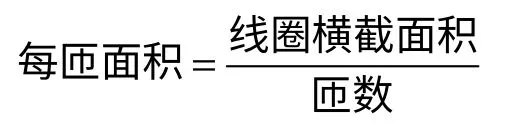
显然模型中每匝面积比实际要大，计算得到的线圈直阻也要小。由于变压器绕组感抗比绕组直流电阻大很多，所以通常情况下的变压器电磁仿真可不必准确考虑绕组的直阻，采用上述计算即可。但对于短路故障匝来讲，由于其短路电流很大（可达几十千安），直阻对电流的影响可观，所以短路匝内的直阻应计算在内。从直阻折算的角度来看，故障匝匝数较少时，虽直阻较小，但折算到一次侧要乘以匝数比的二次方，折算后数值较大，故障匝直阻不可忽略。另外，后面计算要考虑瞬态过渡过程、时间常数以及直阻和感抗的比例关系，所以除故障匝以外的绕组也要考虑线圈直阻的影响。

本文采用的是Infolytica公司的MagNet电磁仿真软件，该软件可以通过线圈属性页内的Strand Area参数来设置每匝有效净截面积，如图4所示，使较准确的直阻参与计算成为了可能。

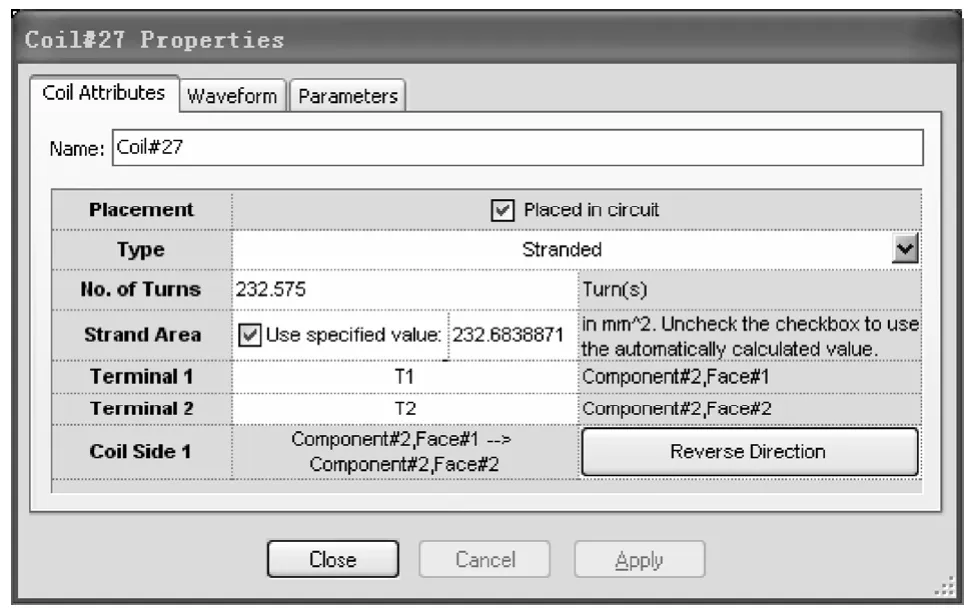
图4 MagNet 中设置每匝有效净截面积Fig.4 The setting of net cross area in MagNet

需要指出的是，对于有限元电磁仿真结果不需要再进行阻抗折算，折算是解析方法，短路匝的直阻变化直接反映到了短路匝内的电流的大小、相位，进而影响一次电流。经验证，通过解析法折算到高压的直阻同仿真直接获取的直阻相差不大。

经过上面的假设和设置后，采用时谐场（时间谐波场）场路耦合计算，自动计算由于短路故障造成的高压并联绕组的电流分配，以及高压侧系统提供的短路电流，包括幅值、相角，进而得到一次侧端口的直阻和感抗。

2.3 简化模型

因计算只需考虑线圈的阻抗和漏抗对电流的影响，所以计算模型可以将构件适当简化，忽略构件损耗对短路电流的影响。图5是在MagNet V7.0中建立的1/2三维简化模型。

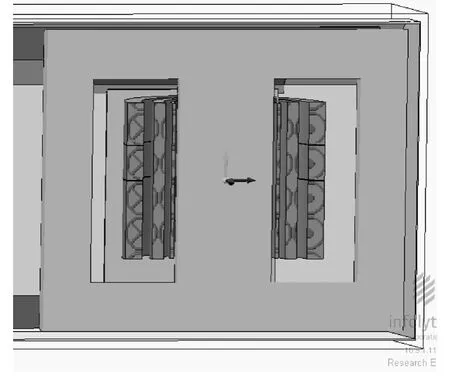
图5 MagNet 中建立的1/2 三维简化模型Fig.5 The 3D simplified model in MagNet

模型中的部件包括铁心、所有工作和故障绕组、夹件腹板、磁电屏蔽和油箱。铁心采用简化的理论圆和椭圆横截面，而不必采用分级；磁屏蔽也采用整张磁板而未分成条状；铁磁材料设为非线性、磁各向同性，铁心和磁屏蔽电导率设为零[9-12]。

3 模型验证

为验证模型和电路连接的正确性，首先计算了额定分接时短路阻抗实验工况，用于验证仿真模型的正确性。

将高压接入额定电流源，中压对地短路运行，假设线圈无短路故障匝，计算高中短路阻抗，软件中电路如图6所示。图中串联绕组为两绕组并联，再与公共绕组串联。

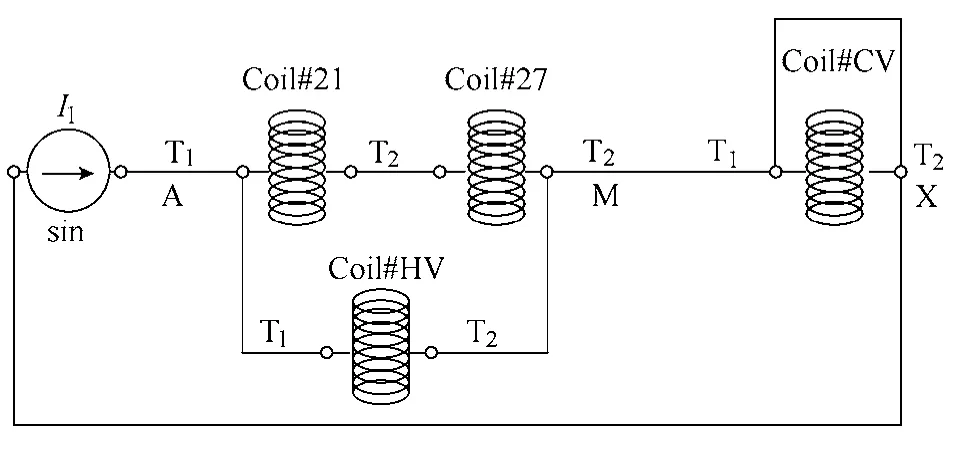
图6 中压短路运行工况电路连接Fig.6 The circuit when medium voltage winding was shorted

采用时谐场场路耦合非线性求解后，得到漏磁场分布、磁场储能及各绕组上的电流和电压。用能量法计算短路阻抗为13.42%，根据绕组电压用阻抗电压定义计算的短路阻抗也为13.42%，设计值为13.24%，误差+1.37%，而且各绕组电流计算结果接近设计值，说明模型建模正确。

4 线圈部分短路计算

采用上述模型，增加假设的短路线匝，进行设置后便可以计算一个高压线圈匝间或段间短路，首端多饼短路甚至各个分接之间短路等工况下的一次短路电流。

虽然假设一次侧电网电压不变，但由于系统阻抗的存在，变压器一次端口电压会有所降低。若实际录波图中测得了故障时间段内变压器端口电压，可以将实际的端口电压作为高压的电压源激励，仿真计算中压发生对地短路时的高压短路电流。若未知变压器一次端口录波电压，计算也可以按图1所示，在高压线路中应串入1.1节计算粗略得到的线路阻抗Zs，再接在系统额定电压上计算，但要认识到不同的电网线路阻抗的差异性。

4.1 无短路故障匝、中压短路运行工况

假设线圈无短路故障匝，施加实际端口电压，计算得到高压线端电流为4 660A。按录波图，在最后一个周期20ms中，通过正负峰值得到高压线端故障电流为4 718A。仿真电流偏差为

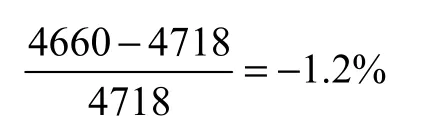
考虑到故障波形有直流衰减量，故故障波形交流分量即稳态值应略小于4 718A，计算误差会更低。仿真值已十分接近实际录波值，这表明存在单纯中压对地短路故障而线圈无短路故障匝的可能。

4.2 线圈饼间短路、中压短路运行工况

模拟假设中压发生对地短路后，引发了线圈某相邻两饼间短路故障情况。施加实际端口电压，仿真计算的高压短路电流，软件中电路连接如图7所示（Coil#20～21线圈为短路故障的两饼线圈）。

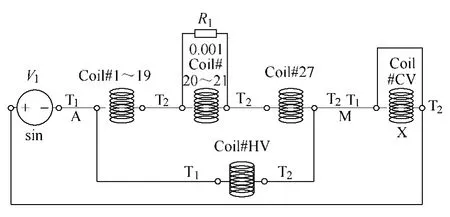
图7 假设存在饼间短路情况下的电路连接图Fig.7 The circuit if two disks was shorted in high voltage winding

采用场路耦合求解后，得到故障情况下的磁场分布如图8所示。得到各绕组的电流（RMS）计算结果包括幅值、相角，如图9所示。

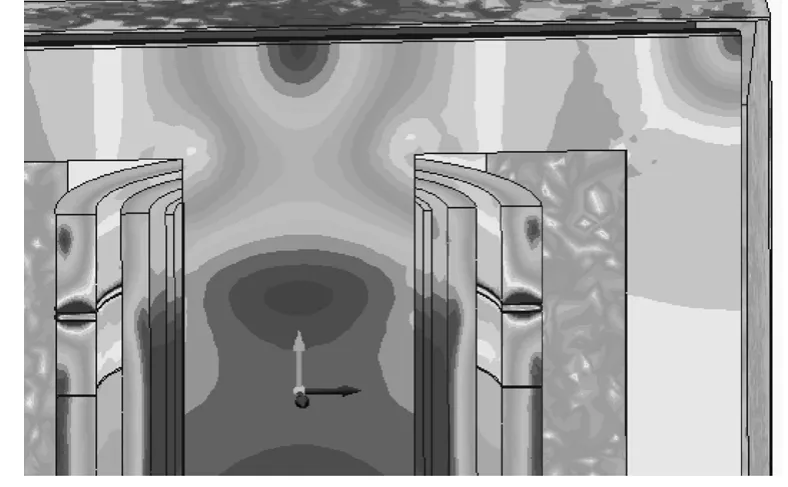
图8 发生饼间短路下的磁通密度分布云图Fig.8 The shaded plot ofBif two disks was shorted

中压绕组电流5 572A，饼间短路电流达47kA，高压线端稳态电流7 004A，与实际录波电流不符，约为实际录波电流的1.5倍。这表明存在中压对地短路故障后继而引发线圈饼间短路故障的可能性小，此故障排除。

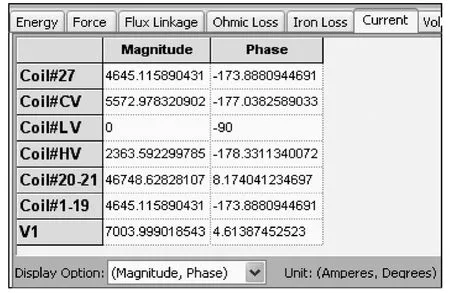
图9 发生饼间短路下的绕组电流Fig.9 The current of windings if two disks was shorted

按照此方法，又计算了其他几种假设线圈短路情形，在此不再列举。经计算对比，假设线圈有部分短路故障匝时的线端稳态电流与实际故障录波偏差较大，表明在中压出口短路的期间，高压绕组没有因短路出现明显变形和局部短路情况，只是单纯的中压对地短路故障。

5 故障匝和故障点的发热计算方法

假设在较短的故障时间内，短路故障匝的热量没有散失，则可以对故障匝内电流在实际故障时间内产生的热量进行积分，可以判断故障线匝能否熔化解裂。

首先计算短路匝电阻上消耗的有功在故障持续时间内产生的热量积分，得到能量E1；同样接触电阻聚集热量时间积分，得到能量E2；并计算出短路故障匝的铜重Wk。设100℃时铜的比热容为398.4J/(kg⋅)℃，则可以得出

（1）若故障接触点能量能使短路接触位置熔化，则温度达到铜的熔点1 084℃，即温度升高近似为1 000℃，此时熔毁的铜重WΔ

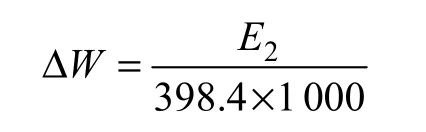
可用于判断故障点熔化情况，与现场故障点对比，从另一方面判断该故障可能性。

（2）若接触故障点未熔断，也可判断短路匝的温度升高KΔ ，以判断故障是否会扩大。

若考虑到温度升高造成的绕组直阻变化，可将直阻的温度折算计算在内，采用国标GB 1094.5中变压器承受短路耐热能力计算公式[8]

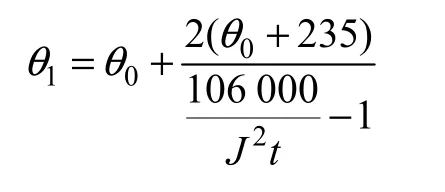
经过对产品的计算分析，故障匝和故障点的发热情况与实际不符。

6 短路瞬态波形计算

式（1）中，故障开始时A相电压的初相角约为α，由录波图得到，已知突然短路电流稳态分量的瞬时值

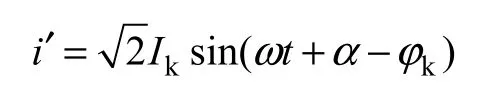
突然短路电流暂态分量的瞬时值为

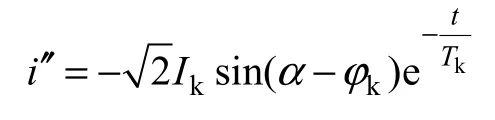
式中，Tk为暂态电流衰减的时间常数，Tk=Lk/Rk，由线路的总阻抗Zk的实部和虚部得到，由图1等效电路可知Zk=Zs+Zt。

至此，短路电流的瞬态波形ki便可以得到了。图10给出了通过数学工具绘制出的某台变压器故障初始时刻短路波形示例。

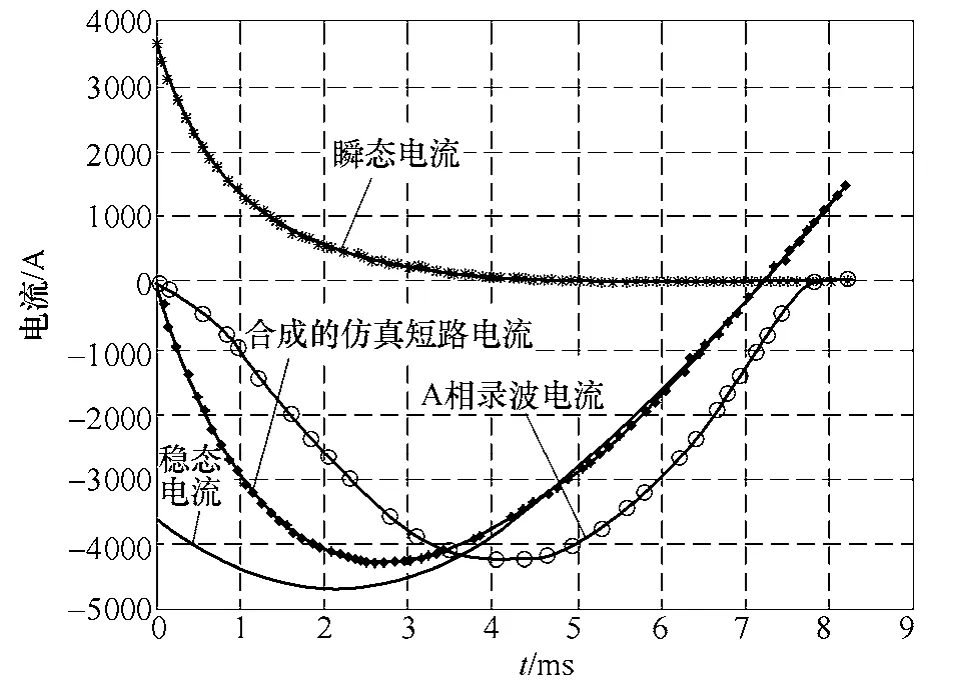
图10 突发短路电流波形Fig.10 The current waveforms of short circuit

通过仿真电流波形和实际故障电流波形的对比，从另一方面考察了故障的可能性。图10中仿真电流数值虽然幅值接近，但相位、周期不符，也从侧面排除了该假设故障。图11是通过人为调整各波形参数得到的比较吻合的波形，便可获知最可能的故障参数。

7 假设短路故障下的短路强度校算

根据4.2节计算出短路电流值，用计算机程序可以计算线圈的短路强度，下表给出了导线应力计算结果。

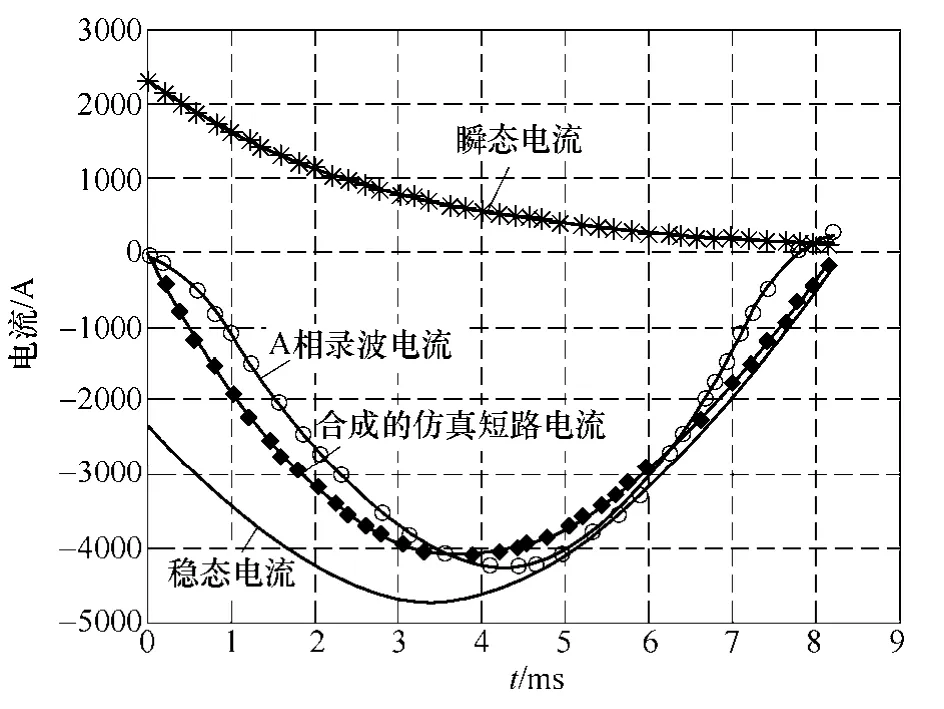
图11 调整后的突发短路电流波形Fig.11 The adjusted current waveforms of short circuit

表 导线应力计算结果Tab. Calculation results of the stress of wire

从上述结果可以看出，高压线圈短路匝导线的拉应力均远远大于导线的屈服强度，表明如果出现高压饼间短路，故障匝承受该短路应力的能力薄弱。

轴向力计算结果表明轴向力最大值201.6tf（1tf=9.8×103N），安全裕度只有0.72，说明如果出现饼间短路，轴向力也很大。

8 结论

本文提供了一种计算突发短路下稳态和瞬态电流的方法，即通过本文提出的场路耦合法模拟各种假设短路故障工况，获得故障状态下的线端短路稳态电流和阻抗参数，再根据故障时刻初相角和计算得到的系统参数，通过数学模型模拟短路发生后的故障瞬态波形，并与实际故障波形的幅值、相位和周期进行对比，同时可计算对比故障点发热熔化情况、绕组短路强度情况，可以判断发生该短路故障的可能性或起始位置及后果。

[1]Bertagnolli G.Short-circuit duty of power trans- formers 3rd revised edition[M].Switzerland:ABB Management Services Ltd Transformers,2006.

[2]陈影,卢继平,阿哈穆得⋅阿里-约瑟夫.考虑磁滞回线的变压器仿真及保护算法[J].重庆大学学报,2005,28(2):39-42.

Chen Ying,Lu Jiping,Ahmed M H Al-Yousis.Simulation and protective algorithm of power transformers considering hysteresis effect[J].Journal of Chongqing University,2005,28(2):39-42.

[3]胡冠中.变压器绕组内部短路故障的数值模拟方法研究[D].杭州:浙江大学,2006.

[4]Nakata T,Takahashi N.Direct finite element analysis of flux and current distributions under specified conditions[J].IEEE Transactions on Magnetics,1982,18(2):325-330.

[5]李琳.具有变压器功能的并联铁心电抗器特性分析与结构设计[J].华北电力大学学报,2009,36(2):1-5.

Li Lin.Analysis and design of a shunt reactor with transformer function[J].Journal of North China Electric Power University,2009,36(2):1-5.

[6]梁振光,唐任远.大型变压器三维瞬态涡流场场路耦合模型[J].电工技术学报,2003,18(5):17-22.

Liang Zhenguang,Tang Renyuan.Coupled field- circuit model of 3D transient eddy current field for large transformers[J].Transactions of China Electro- technical Society,2003,18(5):17-22.

[7]许实章.电机学[M].2 版.北京:机械工业出版社,1988.

[8]GB 1094.5—2008,电力变压器第5 部分 承受短路的能力[S].

[9]程志光.电气工程涡流问题的分析与验证[M].北京:高等教育出版社,2001.

[10]颜威利,杨庆新.电气工程电磁场数值分析[M].北京:机械工业出版社,2005.

[11]谢德馨.三维涡流场的有限元分析[M].北京:机械工业出版社,2001.

[12]张俊杰.新型镜像法杂散损耗试验装置及电力变压器屏蔽的研究[D].北京:华北电力大学,2012.