STA分析：认知多系统模型分析的新方法

邢 强，孙海龙

（1.广州大学教育学院，广东广州 510006；2.暨南大学管理学院，广东广州 510632）

STA分析：认知多系统模型分析的新方法

邢 强1，2，孙海龙2

（1.广州大学教育学院，广东广州 510006；2.暨南大学管理学院，广东广州 510632）

认知研究领域（如记忆、学习）通常通过分离效应来验证或推定存在多个加工系统，但是这种仅仅通过分离效应直接推定存在多系统的方法存在不足.状态痕迹模型分析（STA）具有更大的适应范围.所谓STA模型分析是一个可以确定影响心理变量的数目，调节一个或多个自变量对两个或多个因变量影响的方法.文章从STA模型分析的分析过程、状态痕迹分析与一般线性模型方法之间的关系，以及STA方法的适应等方面加以阐述，以期更好地探讨认知加工过程.

多系统模型；状态痕迹分析（STA）；分离；一般线性模型（GLM）

认知研究中存在许多的争论，特别是认知过程一个还是多个加工系统，即单系统与多系统之争.这种争论在学习、记忆、类别和推理、决策等许多研究领域（如：记忆系统，类别学习系统，推理系统）都可以发现.以往多重加工模型大多是在实验操作实现操作性分离的基础上提出的，通常使用基于一般线性模型（GLM）的方差分析（ANOVA）对数据进行分析，根据交互效应说明存在分离，所谓分离是指人们观察的行为指标被一个或多个变量选择性的影响，即一个自变量影响一个任务，而不影响另一个任务.但是这种分离的思路有其缺陷性，而状态痕迹分析法（State Trace Analysis，STA）具有更大的适应范围，可以克服ANOVA分析的不足，更好检验多重加工模型.

1 基于分离效应推断多系统的缺陷

认知科学最终研究目标是以一种恰当的表征来确认和描述有限数目的大脑加工系统或加工过程.以往研究通常采用操作性分离的方式验证存在多个认知加工系统，其基本研究逻辑：由于不同的因变量基于不同的加工通路，因此，单一自变量对其有不同的影响效果，但已有研究发现，存在分离效应既不是有多个加工系统的充分条件也不是必要条件，通过分离效应推论出多重系统模型只在有限的条件下成立［1］.①存在分离效应要求一个变量只对某个特定行为对象有重要影响，完全不影响其他行为对象，这是不可能的；②进行方差分析的前提是一般线性条件模型，但是数据之间的关系并非都是线性的.笔者以类别学习多系统模型检验为例进行说明.

类别学习中存在单系统与多系统之争［2］，多系统模型［3］（如COVIS模型，COmpetition between Verbal and Implicit Systems（COVIS）Model）认为类别学习系统至少存在一个外显的言语系统和内隐的程序学习系统.外显系统需要占用大量的认知资源如工作记忆、执行功能.而内隐系统主要是特定的视觉区域与特定的行为模式之间的联结，因此会受到按键转换的影响，与这2个系统相对应的是基于规则（RB）和信息整合类别结构（II）.根据多系统理论模型假设，工作记忆削弱基于规则类别学习的成绩，不影响信息整合类别结构的成绩，因此完成类别学习后再完成一个工作记忆任务会削弱基于规则类别学习结构，而不影响信息整合类别结构［4］，此外考虑到训练效应，可以假定记忆负荷与试次数通过类别学习系统多信息整合与基于规则任务产生影响（如图1）.

DUNN等［5］运用STA法对NOSOFSKY等［6］实验进行检验.NOSOFSKY等［6］通过按键来学习基于规则的类别学习或者信息整合的类别学习.对于基于规则的类别学习，学习包括8×50试验（trials），训练后，最后2个Block要求被试对反应的按键翻转，比如在学习阶段按键是类别A按F，类别B按J键，这时对于类别A按J键，类别B按F键.从图2（a）上可见，这是和COVIS预测一致的，反应任务的改变使得在2种类别结构上发生分离效应，即转换按键削弱信息整合类别结构，不影响基于规则类别结构.作者认为由此验证了类别学习多系统模型理论.但是运用STA分析可以发现，尽管存在着操作性分离，但是其结果的改变仍然是和一个潜在变量相关的，图2（b）是一个状态痕迹图（state-trace plot）.横坐标和纵坐标分别是基于规则和信息整合类别结构，从横坐标RB来看，控制组与按键转换组成绩存在显著差异，从纵坐标II看，灰色实心标记分别代表控制组和按键转换组之间成绩没有显著差异.由此可知，基于规则和信息整合类别结构之间存在操作性分离效应，但是图2（b）可见所有的成绩与单一的潜在变量相关.

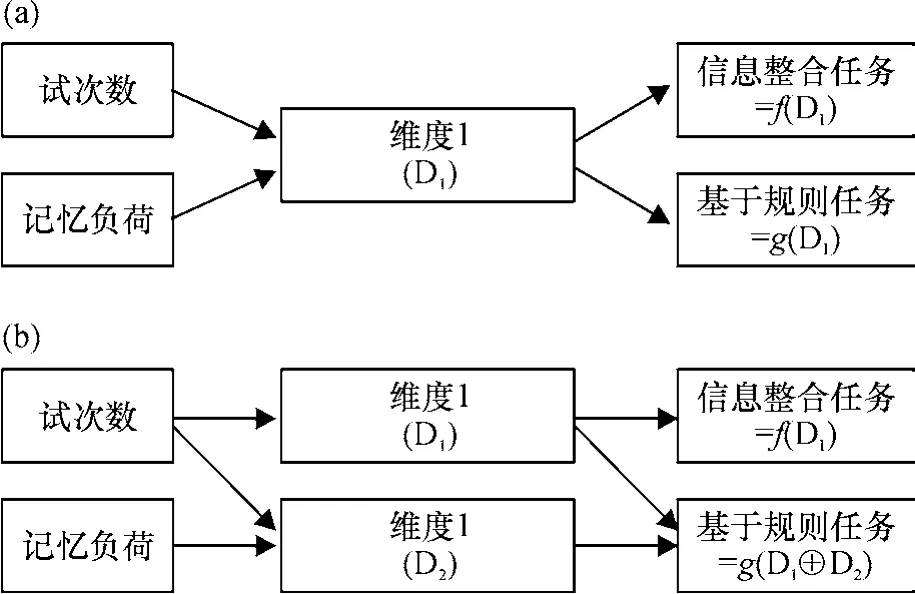
图1 单维度和双维度模型示意图Fig.1 A model for the single dimension and two dimensions

2 STA的统计程序与数理推断

状态痕迹分析是一种用来确定干预心理变量数量的方法，它可以调节一个或多个自变量对2个或多个因变量的影响［4］.操作性分离通常使用的统计方法为方差分析，状态痕迹分析法与方差分析的理论基础是不同的.方差分析涉及的是一般线性模型；STA涉及的是在结果空间上一组单调的次序结构的点.如在类别学习中，类别结构被看作是一个有2个水平的自变量（例如，RB vs.II），根据一般线性模型的假设自变量与一个单独的因变量（如类别成绩）直接是线性相关的；如果运用STA，则2个类别结构分别被定义为不同的因变量，并非与其他自变量有线性相关.DUNN等［7］初步进行了论述，而NEWELL等［8］详细描述了这种统计方法应用在类别学习等具有研究中的过程.

2.1 STA的统计程序

图2 NOSOFSKY等实验数据方差分析（a）与状态痕迹图（b）Fig.2 The experimental data of variance analysis in NOSOFSKY，et al.（a）and figure of the state trace analysis（b）

STA分析的统计过程包括2个部分：①模型拟合部分，②模型检验部分.在模型拟合阶段，主要使用2种模型拟合数据，次序受约束两维度模型（order-restricted two dimensional model）和次序受约束的单维度模型（orderrestricted one dimensional model），首先使用两维度模型加以拟合，其允许状态痕迹是2个维度的（如非单调），但是需要指定一些数据点的优先顺序［8］.通过这个模型排除违反单调性的数据，这些数据反映是由于非预期的实验或测量错误导致的.例如，双维度模型强加一个限制：被试通过训练，在基于规则和信息整合的类别任务上的分类成绩不应该是降低的.在双维度模型拟合基础上，使用次序受约束的单维度模型（order-restricted one dimensional model），其允许的状态痕迹为单维度的.但这种单维度模型会增加额外的强制条件，将数据在2个因变量上按照一定的优先顺序加以排列.在模型检验部分，使用蒙特卡罗模拟法（Monte Carlo simulation）这种实验分布测量的.

在实际操作中，状态痕迹图是运用状态痕迹分析法进行分析的重要工具.这是一些不同的实验条件与2种因变量相伴变化的散点图.通过这个图可见是否根据不同的实验条件数据落在一个单调递增或者递减的曲线上.尽管对于2个因变量的函数表达式是不清楚的（在图1中是用f和g表示）.如果2个任务依赖于相同的潜在维度，在状态痕迹图上它们相关数据应该落在相同的单调递增曲线上（图3）.从状态痕迹图上笔者发现了分离效应，但是依然属于单维度.

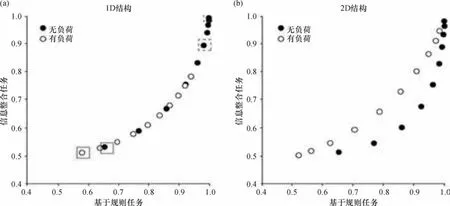
图3 理想化的STA图（单维度和双维度）Fig.3 Idealized STA figure（single dimension and two dimensions）

2.2 最大线性估计

状态痕迹分析法的数理基础主要是基于最大线性估计（MLE）和零假设统计检验（NHST）.MLE／NHST方法有自己的优势，它能够轻易的应用于当前的数据，不需要每个模型具有特定的先验概率分布.但是这种方法的缺陷是NHST只能被拒绝，与贝叶斯因素方法相反，零假设的证据（如一个单维度模型）不能直接与备择假设的证据（如一个双维度模型）相比较.

MLE／NHST方法使用强迫最大线性估计进行模型拟合.对于每个模型拟合p值的零假设估计是使用基于数据信息参数引导数据模型方法（PBCM）的蒙特卡洛程序［9］.

这里为说明数据推理过程，笔者采用记忆负荷与实验试次影响基于规则和信息整合类别学习类别的实验为例（见图1），记忆负荷主要通过经典的Stroop任务来进行操作，实验分为Stroop条件和无Stroop任务的控制条件.具体在每个条件内，假设观察的对象（如每个被试的平均正确率）是独立的，共同方差估计的正态分布是根据条件方差内的共同方差估计得到的.令xj和yj分别在不同的调节下（比如类别学习研究领域，在基于规则和信息整合任务条件），对于一个给定的模型，对于相一致的条件，令j和为预测变量．这个模型数据的拟合使用如下方程给出：

对数据拟合3个模型：痕迹模型（trace model）、单维度模型（one-dimensional model）、不重叠模型（nonoverlap model）.根据不同模型强制条件的约束，可以定义不同的模型.作为限制条件，代表两两不同的标志，其中令ujk＝为在基于规则任务上条件j和条件k的差异，令vjk＝为相应的在信息整合任务上条件j和条件k的差异．由痕迹模型在基于规则和信息整合两种任务中指定一个定序的条件，如控制组和stroop条件组内，对于两个任务来说它需要的是一个不递减的与组块相关的函数.每一个排序都是可以根据相关条件差异的信号来得到的.对于部分的j和k即信号（ujk）＝信号（vjk）＝1，对于单维度模型则是指定一个额外的限制条件，在两种任务上所有的两两差异值，即，对于所有的j 和k，信号（ujk）＝信号（vjk）．最后，则根据单维模型和状态痕迹模型之间的嵌套产生不重叠模型，即对于所有j∈控制组和k∈stroop组，信号（ujk）＝信号（vjk）＝1．目前，上述STA的分析过程可以直接通过R语言程序加以实现［10］.

3 STA与GLM的关系

虽然STA与GLM之间的理论基础不同，但是两者并非是完全没有关系的，一定条件下可以根据两者之间相互推断.根据图1，假定有3个自变量，分别为b，c，和d．即b为实验组块，c为类别类型，d为有无工作记忆任务.假设每个变量具有2个水平，即2个水平分别被编码为0和1.令y是在实验条件下的平均成绩.根据一般线性模型（GLM），可以写为

y0的点对应y1的每个联合变量．这里的b，d就被称为在变量c上的状态痕迹．那么什么条件下是单维度的呢？是否是单维度主要是由能够映射参数的函数所决定［11］，这里是b，d所决定．状态痕迹的维度是由函数矩阵的等级所决定．函数矩阵Dy是一个遵循每个参数函数的多元函数的偏导矩阵.根据A3，可以得到：

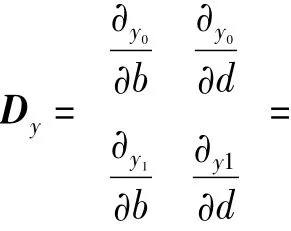
（1）b没有主效应或没有与b的交互作用，即a1＝a3＝a5＝a7＝0；

（2）d没有主效应或没有与d的交互作用，即a2＝a3＝a6＝a7＝0；

（3）b和d既没有主效应，其他变量也与c没有交互作用，即a1＝a2＝a5＝a6＝0；

（4）b和c或者d和c之间没有交互作用，即a5＝a6＝a7＝0；

（5）b和d既没有主效应，它们之间也没有交互作用，即a1＝a2＝a3＝0；

（6）所有的效应量相等，即a1＝a2＝a3＝a4＝a5＝a6＝a7．

如果对数据进行方差分析，当数据符合任何上述列出的结果时，c上相应的状态痕迹图将是一维．然而，变量与一个或多个其他变量有交互作用，不足以得出在c状态痕迹图是双维的结论，因此当方差分析存在交互作用，存在操作性分离时并不一定对应双维的状态痕迹图.

4 展 望

STA可以运用到许多认知的研究主题中，如类别学习、学习决策（JOL）、对比和视觉记忆［12］.STA的运用使得许多通过操作性分离的存在解释多重加工系统的结果受到挑战［13］.但是ASHBY［14］对于STA统计方法提出质疑，其认为STA假设状态痕迹图中分离的曲线表明基于不同的加工系统的观点是不正确的，只有一个参数变化的模型同样可以产生任何形式的状态痕迹图，状态痕迹图运用并不能直接推断出潜在的加工系统数目.此外，眼动、ERP等认知神经技术的研究中如何使用状态跟踪分析提高推论的准确性等问题还未涉及，还需要进一步探索STA的适用条件.

参考文献：

［1］ NEWELL B R，DUNN J C.Dimensions in data：Testing psychological models using state-trace analysis［J］.Trend Cogn Sci，2008，12：285-290.

［2］ ASHBY F G，O’BRIEN J B.Category learning and multiple memory systems［J］.Trend Cogn Sci，2005，9：83-89.

［3］ ASHBY F G，AlFONSO-REESE L A，TURKEN A U，et al.A neuropsychological theory of multiple systems in category learning［J］.Psy Rev，1998，105：442-481.

［4］ ZEITHAMOVA D，MADDOX W T.Dual task interference in perceptual category Learning［J］.Memory Cogn，2006，34：387-398.

［5］ DUNN J C，NEWELL B R，KALISH M.The effect of feedback delay and feedback type on perceptual category learning：The limits of multiple systems［J］.J Exper Psy：Learn，Mem，Cognit，2012，38：840-859.

［6］ NOSOFSKY R M，STANTON R D，ZAKI S R.Procedural interference in perceptual classification：Implicit learning or cognitive complexity？［J］.Mem Cogn，2005，33：1256-1271.

［7］ DUNN J C，JAMES R N.Signed difference analysis：Theory and application［J］.J Mathem Psy，2003，47：389-416.

［8］ NEWELL B R，DUNN J C，KALISH M.The dimensionality of perceptual category learning：A state-trace analysis［J］. Mem Cogn，2010，38：563-581.

［9］ WAGENMAKERS E J，RATCLIFF R，GOMEZ P，et al.Assessing model mimicry using the parametric bootstrap［J］.J Math Psy，2004，48：28-50.

［10］PRINCE M，HAWKINS G，LOVE J，et al.An R package for state-trace analysis［J］.Behav Res Meth，2012，44：644-655.

［11］DUNN J C，KIRSNER K.What can we infer from double dissociations？［J］.Cortex，2003，39：1-7.

［12］DUNN J C.The dimensionality of the remember-know task：A state-trace analysis［J］.Psy Rev，2008，115：426-446.

［13］DUNN J C，KALISH M，NEWELL B R.State-trace analysis can be an appropriate tool for assessing the number of cognitive systems：A reply to Ashby（2014）［J］.Psy Bull Rev，2014，21（4）：947-954.

［14］ASHBY F G.Is state-trace analysis an appropriate tool for assessing the number of cognitive systems？［J］.Psy Bull Rev，2014，21（4）：935-946.

The state trace analysis：A new method for analysis of multiple system model

XING Qiang1，2，SUN Hai-long2
（1.School of Eduction，Guangzhou University，Guangzhou 510006，China；2.Management School，Jinan University，Guangzhou 510632，China）

In the field of cognitive research（such as memory，learning），there is now much evidence that cognitive processes are mediated by multiple systems through the separation effect.The state trace analysis（STA）has a larger scope of adaptation.The state trace analysis is a method to determine the number of psychological variables，how one or more independent variables affect the two or more factors.This paper introduces the general statistical program and mathematical reasoning process of STA，and the relationship between the state trace analysis and the general linear model.At the end of the paper，the next stage of the research is pointed out.

multiple system model；the state trace analysis（STA）；separation；the general linear model （GLM）

G 44

A

【责任编辑：陈 钢】

1671-4229（2015）05-0083-05

2015－08－20；

2015－09－08

国家自然科学基金资助项目（31571144）；广东省教育科学规划资助项目（2013WYXM0095）；广东省高校质量工程资助项目（2014GXJK059）；广州市属高校“羊城学者”科研资助项目（1201561646）

邢 强（1973－），男，教授，硕士生导师.E-amil：Qiang_xingpsy＠126.com