关于有理函数系数微分方程的亚纯解

袁文俊，刘 芝，孟凡宁，傅懋准

（广州大学a.数学与信息科学学院；b.数学与交叉科学广东普通高校重点实验室，广东广州 510006）

关于有理函数系数微分方程的亚纯解

袁文俊，刘 芝，孟凡宁，傅懋准

（广州大学a.数学与信息科学学院；b.数学与交叉科学广东普通高校重点实验室，广东广州 510006）

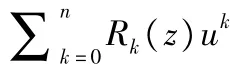
亚纯解；线性无关解；微分方程；有理系数

1 Introduction and main results

In the past 30 years，many authors have been interested in the maximum number M of distinct meromorphic solutions and about the maximum number L of linearly independent meromorphic solutions of the differential equation

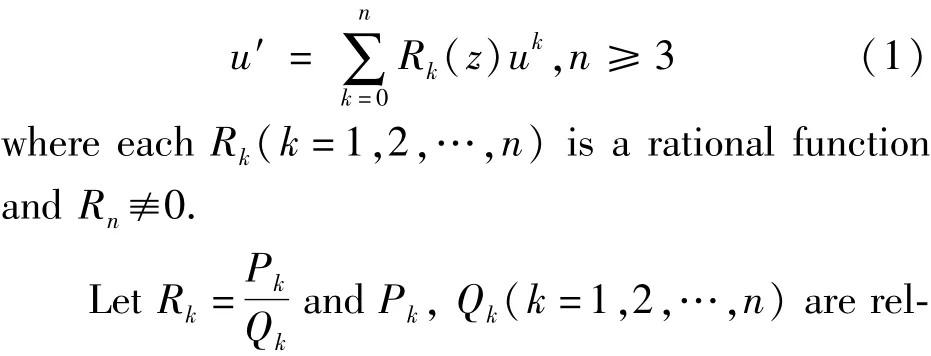
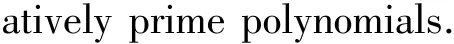
In order to state our results in the paper，we need some notations and denotations.

The number n is the highest order of Eq.（1），the number d is distinct zeros of Rn，and dkdenotes the degree of Pkfor each 0≤k≤n．Let H denote the lowest common polynomial of Q0，Q1，…，Qn－1and the number d*is distinct zeros of H.can possess at most a finite number of distinct meromorphic solutions.

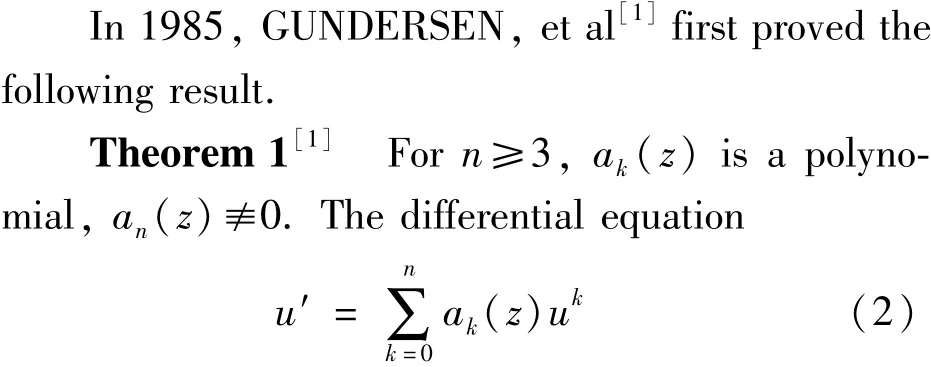
In 1987，GAO［2］had generalized the result above to Eq.（1）and had got that Eq.（1）can possess at most a finite number of distinct meromorphic.

In 1987，HE［3］gave an estimation below，which depends on n＋2 parameters.

Theorem 2［3］For n≥3，the differential Eq. （2）can have at most K distinct meromorphic solutions where K is a constant depending on n，dk，1≤k ≤n meromorphic solutions.

In 1989，ZHANG［4］generalized Theorem 2 to the rational coefficients and also got the result that Eq.（1）can have at most K distinct meromorphic solutions where K is a constant depending on n，dk，1 ≤k≤n meromorphic solutions.

Remark 3 The maximum number M of distinct meromorphic solutions and the maximum numbers L of linearly independent meromorphic solutions all depend on n and other n＋2 parameters in Theorem 2.

In 1992，YUAN［5］showed that we can estimate the maximum number M of distinct meromophic solutions of（2）in terms of n and dnonly.

Theorem 4［5］Eq.（2）can possess at most M distinct meromorphic solutions，where

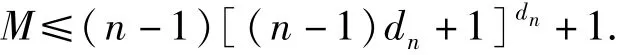
In 2008，GUNDERSEN［6］proved the following two theorems.

Theorem 5［6］The Eq.（2）can possess at most L linearly independent meromorphic solutions，where L satisfies the following：

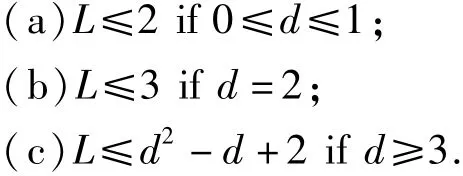
Theorem 6［6］Eq.（2）can possess at most M distinct meromorphic solutions，where

Theorem 6 maybe is the first general estimation for M in terms of d and n only.

In the paper，we generalize both Theorems 5 and 6 to Theorems 7 and 10 by using the same method and arguments of GUNDERSEN in Ref.［6］and obtain the following results.

Theorem 7 Eq.（1）can possess at most L*linearly independent meromorphic solutions，where L*satisfies the following：

This example gives equality in Theorem 7（a），because here we have d＋d*＝1 and L*＝2．

Theorem 10 Eq.（1）can possess at most M*distinct meromorphic solutions，where

where d*is the number of distinct zeros of H.

Example 11 For Example 8，we know it possesses 2n－1 distinct meromorphic solutions，namely 0，ei，ei／z（eiis an（n－1）－th root of unity，i＝1，2，…n－1）.This example also shows that Theorem 10 is sharp，because here we have d＋d*＝n and M*＝2n－1.

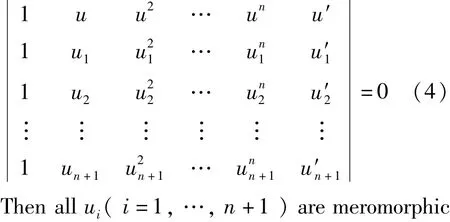
Example 12 Let u1，u2…un＋1（n≥3）be n＋1 distinct rational functions.Consider the equationsolutions of Eq.（4）with rational coefficients.So，Eq.（4）has at least n＋1 meromorphic solutions. Here we have d＋d*≥2 and n＋1≤1＋（n－1）［（d ＋d*）（d＋d*－1）＋1］.

Example 13［1］If n is a positive integer，then the equation

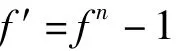
possesses n constant solutions，where the constants are the n－th roots of unity.This gives an equality in Theorem 10，because we have d＋d*＝0 and M*＝n．

This paper is organized as follows：In Section 2，the lemmas are given.The proofs of Theorems 7 and 10 are respectively given in Sections 3 and 4.

2 Lemmas

In order to prove Theorems 7 and 10，we need to improve some lemmas.

Lemma 14［7－8］Let Q1，Q2and Q3be three relatively prime polynomials which satisfy

Lemma 15 For Eq.（1），the following statements hold：

（a）if u is any meromorphic solution of（1），then u is a rational function and HPnu is a polynomial；

（b）if u1and u2are two distinct meromorphic solutions of（1），then any zero of u1－u2must be a zero of HPn.

Proof. If u is a meromorphic solution of（1），then from the classical theorem of Malmquist［9］，we know u is a rational function.Suppose that u（z）is a meromorphic solution of Eq.（1）.If z0is a pole of u（z）of multiplicity atτ，set

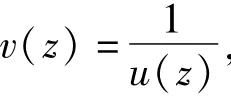
then z0is a zero of v（z）of multiplicityτ.And v（z）satisfies the equation

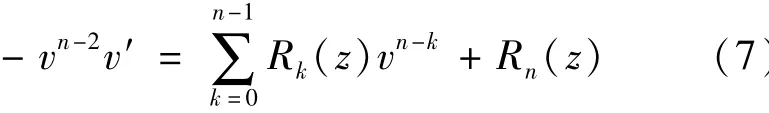
From Eq.（7），we have two cases.

Case 1.When z0is not the pole of arbitrary Rk，（k＝0，1…，n－1），so z0must be a zero of Rnof multiplicity at leastτ.

Case 2.When z0is a pole of some Rki（i＝1，2，…，m）of multiplicityτki.We have two subcases：

Subcase 2.1：we haveτki＜（n－ki）τfor all ki，and let

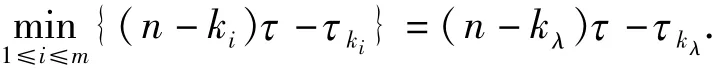
therefore，z0is a zero of Rnof multiplicity at least min ｛τ，（n－kλ）τ－τkλ｝．

Subcase 2.2：whenτkδ≥（n－kδ）τ，z0is a zero of Rnof multiplicity at leastτ［2，10］.

is a polynomial.

In fact，if z0is a pole of u（z）of multiplicityτ and not a zero of all Q1，Q2，…Qn.then z0must be a zero of H（z）P（z）of multiplicity at leastτ，and z0is not a zero of Qn.It is easy to prove that the assertion holds in Case1 and Subcase 2.2.Nevertheless，Subcase 2.1 needs to be discussed.When

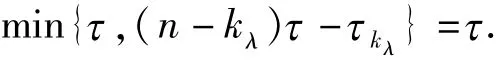
Obviously，the assertion is right.When

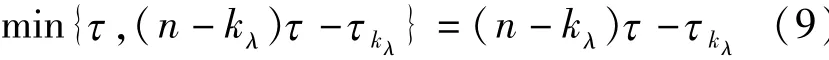
We know that H denotes the lowest common pol-ynomial of Q0，Q1，…，Qn－1，so z0is a zero of H（z）of multiplicityτh≥τkλ．Then

so，it is right when the assertion in Subcase 2.1.

If z1is a zero of Qnof multiplicity k，z1must be a zero of one or more than one of Q1（i＝0，1…，n－1）of multiplicity at least k.

Thus，the assertion is right.For the sake of convenience without loss generally，we can suppose that Qn≡1．This proves（a）.

Next，if u1and u2are distinct meromorphic solutions of（1），and z0is a zero of u1－u2，then from the uniqueness of solutions of（1），z0is a pole of both u1and u2.Then（a）implies HPn（z0）＝0，which proves（b）.This proves this lemma.

Lemma 16［6］Assumption that u1，u2，u3are three meromorphic solutions of Eq.（1），such that u1－u2and u1－u3are linearly independent.Then there exists a rational function R such that the three functions

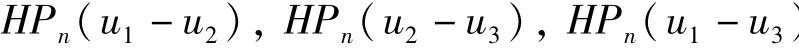
are polynomials whose zeros all occur at zeros of HPn.By dividing all three of these polynomials by another polynomial，we know that there exists a rational function R such that the three functions

Suppose that Q1and Q3are both constants，so u1－u2and u1－u3are linearly dependent，which contradicts the hypothesis.Thus，Q1，Q2，Q3are not all constants.Because

and all the zero of Q1，Q2，Q3occur at zeros of HPn，we can apply Lemmas 14 to Eq.（11），and obtain （10）.So we can prove Lemma 16.

Lemma 17 Let u1，u2，…，uk，（k≥3），be k meromorphic solutions of（1），so there are k－1 functions

Proof． Let i and j be two distinct integers satisfying 2≤j≤k and 2≤j≤k.Due to the hypothesis，u1－uiand u1－ujare linearly independent.From Lemma 16，there exists rational function S such that the three functions

are k－1 linearly independent relatively prime polynomials whose zeros all occur at zeros of HPn.

Hence，if z0is a zero of R（u1－uj）of multiplicity μ，and some j satisfying 2≤j≤k，so we can deduce that

Because HPnhas d distinct zeros，R（u1－uj）has at most d＋d*distinct zeros，2≤j≤k.Therefore，according to（14），we get

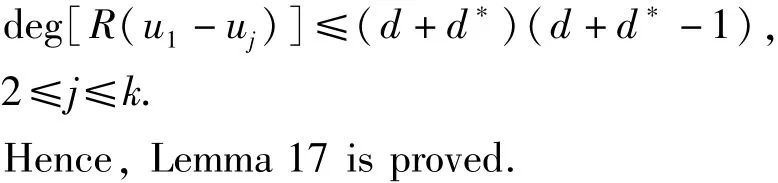
Lemma 18 Suppose that u1be a fixed meromorphic solution of Eq.（1），and R is a rational function，where R≢0，the function R（u1－u）is a polynomial，for any meromorphic solution u of（1）. If α is an integer and for any meromorphic solution u of（1），we have

which each Sk，j＋1is a rational function，and where Sn（j＋1）－j，j＋1≢0 for any j.Because T（a＋1）≡0，we obtain

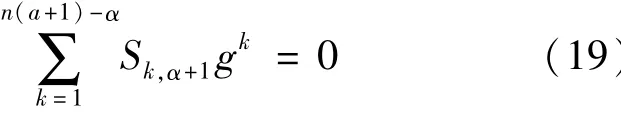
whereeachSk，α＋1isarationalfunction，and Sn（α＋1）－α，α＋1≢0．Observe that（19）is a functional equation in g with rational function coeffcients，that is satisfied by any rational g in（17），i.e.g＝uu1.Both members of Eq.（19）multiplied by a polynomial make Eq.（19）which the left side of（19）is a polynomial in g of degree n（α＋1）－α，we get basic field theory that Eq.（19）can possess at most n （α＋1）－α distinct rational solution g of the form g ＝u－u1.It follows that Eq.（1）can possess at most n（α＋1）－α distinct meromorphic solutions u.So Lemma 18 is proved.

Lemma 19［6，11］Suppose that u1，u2，…，uk，（k≥2）be k linearly independent meromorphic solutions of（1），and R is a rational function，where R≢0，so R（u1－uj）is a polynomial for all j satisfying 2 ≤j≤k.If we let

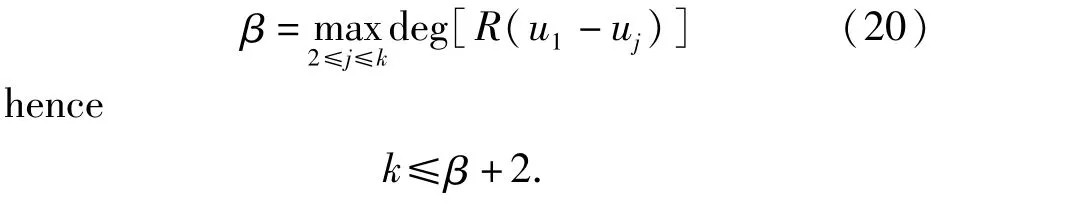
Lemma 20 Suppose that u1and u2be two distinct meromorphic solutions of（1）and for any meromorphic solution u of（1），the two functions u1－u2and u1－u are linearly dependent.Then Eq.（1）can admit at most n distinct meromorphic solutions.

Proof． Suppose that u is any meromorphic solution of（1），so there exists a constant C＝C（u）such that

Both members of the Eq.（25）multiplied by a polynomial make Eq.（25）which the right side of （25）is a polynomial in C of degree n，there exist at most n distinct meromorphic solutions.Hence Lemma 20 is proved.

3 Proof of Theorem 7

The way to prove Theorem 7 is similar to Theorem 5.

Proof． To prove part（a），we need to suppose that 0≤d＋d*≤1．So，provided that Eq.（1）possesses at most two linearly independent meromorphic solutions，so part（a）is immediately true. Therefore，the assumption is that Eq.（1）possesses three linearly independent meromorphic solutions u1，u2，u3.Hence，according to Lemma 16，there is a rational function R such that the three functions

If d＋d*＝0，so（26）is a contradiction.If d ＋d*＝1，so（26）suggests that the three rational function R（u1－u2），R（u2－u3），R（u1－u3）are all constants，which contradicts our assumption，so u1，u2，u3are linearly independent.These contradictions show that our assumption that u1，u2，u3are linearly independent，must be false.So any three meromorphic solutions of（1）must be linearly dependent，when d＋d*satisfies 0≤d＋d*≤1，which proves part（a）.

In order to prove parts（b）and（c），we assume that d＋d*≥2．We suppose that there exist k linearly independent meromorphic solutions u1，u2，…，uk，where k≥4，otherwise，there is nothing to prove.So according to Lemma 17，there is a rational function S such that

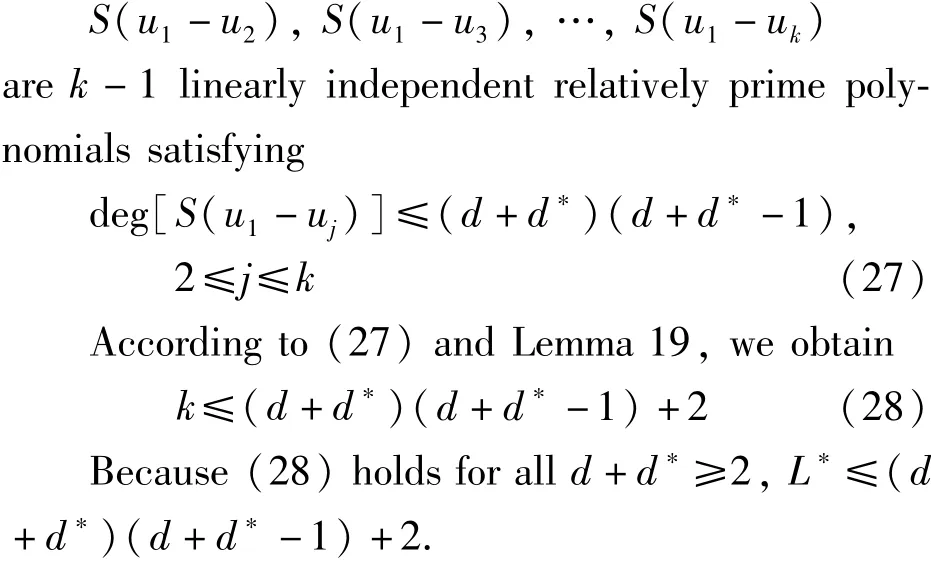
We prove part（b）.We let d＋d*＝2 and make the assumption that（1）possesses four linearly independent meromorphic solutions u1，u2，u3，u4，since otherwise，there is nothing to prove.In this case，we let k＝4 in（27），which gives

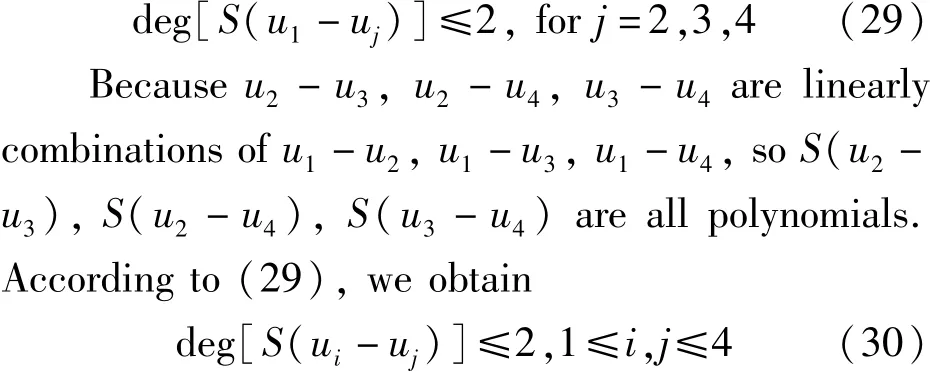
From the proof of Lemma 17，we get that all the zeros of S occur at zeros of HPn.So by Lemma 15，all the zeros of S（ui－uj）（1≤i，j≤4）occur at zeros of HPn.Because d＋d*＝2，Suppose a and b be the two distinct zeros of HPn．Then according to（30），each of the six functions

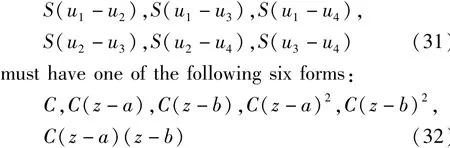
which C is a non-zero constant.Furthermore，since u1，u2，u3，u4，are linearly independent，there must be a one-to-one correspondence between the six functions in（31）and the six forms in（32）.

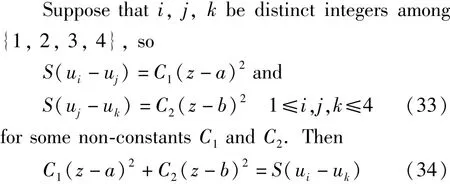
But S（ui－uk）must have one of the six forms in（32），and this contradicts（34）.This contradiction means that our assumption in（33）must be false. Hence，we can suppose without loss of generality that

But S（uj－u2）must have one of the forms in （32），which contradicts（37）.This contradiction implies that（36）cannot hold for i＝1.Analogously we obtain a contradiction in（36）when i＝2，3，or 4.Hence，we get a contradiction in all possible cases，which means that our original assumption that u1，u2，u3，u4are linearly independent，must be false.There can exist at most three linearly independent meromorphic solutions of Eq.（1），when d＋d*＝2.So it proves part（b）.This proves Theorem 7.

4 Proof of Theorem 10

The way to prove Theorem 10 is similar to Theorem 6.

Proof． First，let 0≤d＋d*≤1．So according to Theorem 5（a），there exist at most two linearly independent meromorphic solutions of（1）.We have two cases.

Case 1.1.Assume that Eq.（1）does not possess two linearly independent meromorphic solutions. In this case，if u1is a meromorphic solution of（1），where u1≢0，then any meromorphic solution u of （1）must have the form u≡Cu1，where C is a constant.Substituting u≡Cu1into（1）gives

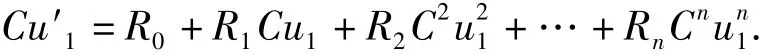
Both members of the equation above multiplied by a polynomial and choose a point z0such that HPn（z0）≠0 and u1（z0）≠0．Then

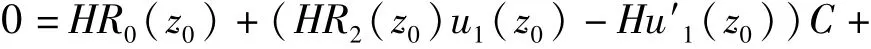
Because the right side is a polynomial of degree n in C，it has at most n possible values for C．It follows that the maximum number M of distinct meromorphic solutions of（1）satisfies M≤n．On the other side，if it does not exist a meromorphic solution u1of（1），where u1≢0，then M≤1.Therefore，Case 1.1 yields M≤n.

Case 1.2.Assume that Eq.（1）has two linearly independent meromorphic solutions u1and u2.We can suppose there exist at least three distinct meromorphic solutions of（1），since otherwise，there is nothing to prove.There are two subcases.

For the first subcase，assume that there exists a meromorphic solution u3of（1）such that u1－u2and u1－u3are linearly independent.So according to Lemma 16，there exists a rational function R such that three functions

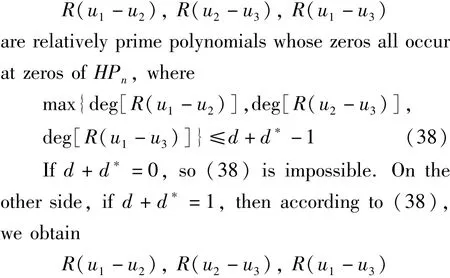
are all constants，But this suggests that u1－u2and u1－u3are linearly dependent，which contradicts our assumption.Hence，this first subcase cannot occur.

For the second subcase，it assumes that for any meromorphic solution u of（1），the two functions u1－u2and u1－u are linearly dependent.According to Lemma 20，we get that M≤n．Therefore，Case 1.2 yields M≤n．

Case 1.1 and case 1.2 show that M≤n，when 0 ≤d＋d*≤1．

Now we assume that d＋d*≥2 and（1）possesses at least three distinct meromorphic solutions，since otherwise，there would be nothing to prove. There are two cases.

Case 2.1.Assume there are two distinct meromorphic solutions u1and u2of（1），so for any mero-morphic solution u of（1），u1－u2and u1－u are linearly dependent.So according to Lemma 20，M≤n.

Case 2.2.Suppose there is k distinct meromorphic solutions u1，u2，…，uk，（k≥3）of（1），such that the k－1 functions

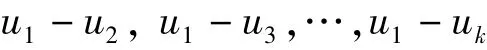
are linearly independent.We choose k to be as large as possible，so that if u is any meromorphic solution of（1），then the k functions

According to（39）and（40），it has that if u is any meromorphic solution of（1），then R（u1－u）is a polynomial satisfying

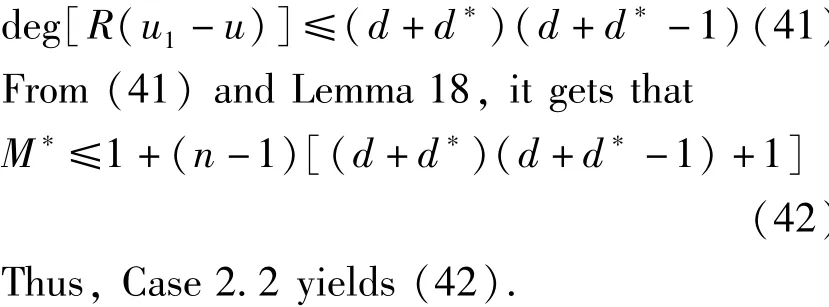
Case 2.1 and case 2.2 show that Theorem 10 hold when d＋d*≥2．Therefore，it shows that M*≤n when 0≤d＋d*≤1．Then Theorem 10 is proved.

Acknowledgment

The authors finally wish to thank Professor GUNDERSEN G G for supplying his useful reprints and suggestions.

［1］ GUNDERSEN G G，LAINE I.On the meromorphic solutions of some algebraic differential equation［J］.J Math Anal Appl，1985，111（1）：281-300.

［2］ GA0S A.On the number of meromorphic solutions of one class of ordinary differential equations［J］.Acta Math Sin，1987，30（2）：160-167.

［3］ HE Y Z.On the number of solutions of a class of ordinary differential equations［J］.Kexue Tongbao，1987，32（7）：80-85.

［4］ ZHANG X K.On the number of meromorphic solutions of some algebraic differential equations［J］.J Hunan NorUniv，1989，12（1）：16-20.

［5］ YUAN W J.On the number of meromorphic solutions of some first order algebraic differential equations［J］.J Math Anal Appl，1992，167（2）：316-321.

［6］ GUNDERSEN G G.Meromophic solutions of differential equation with polynomial coefficients［J］.Comput Math Funct Th，2008，8（1）：1-14.

［7］ LANG S.Algebra［M］.3rd ed.New York：Springer，2002：194.

［8］ NATHANSON B M.Elementary methods in number theory［M］.New York：Springer，2000：182.

［9］ MALMQUIST J.Sur les fonctions à un nombre fini des branches définies par les équations différentielles du premier ordre ［J］.Acta Math，1913，36（1）：297-343.

［10］GA0S A.On the number of meromorphic solutions of one class of ordinary differential equations［J］.Kexue Tongbao，1987，30（2）：1652-1653.

［11］GUNDERSEN G G，LAINE I.Existence of meromorphic solutions of algebraic differential equation［J］.Math Scand，1990，67（1）：35-55.

【责任编辑：周 全】

On meromophic solutions of differential equation with rational coefficients

YUAN Wen-jun，LIU Zhi，MENG Fan-ning，FU Mao-zhun
（a.School of Mathematics and Information Sciences；b.Key Laboratory of Mathematics and Interdisciplinary Sciences of Guangdong Higher Education Institutes，Guangzhou University，Guangzhou 510006，China）

meromorphic solutions；linearly independent solutions；differential equation；rational coefficients

0175.4

：A

date：2015－05－25； Revised date：2015－07－23

s：This work was supported by the Visiting Scholar Program of Department of Mathematics and Statistics at Curtin University of Technology，the support with the NSF of China（11271090）and NSF of Guangdong Province（2015A030313346，S2012010010121）.

0175.4

A

1671-4229（2015）05-0001-08

Biography：YUAN Wen-jun（1957－），male，professor，Ph.D.E-mail：wjyuan1957＠126.com