计入风重耦合效应高耸结构顺风向响应分析

钟振宇楼文娟

（1.浙江工业职业技术学院建筑工程学院，浙江绍兴，312000；2.浙江大学建筑工程学院，浙江杭州，310058）

计入风重耦合效应高耸结构顺风向响应分析

钟振宇1，2楼文娟2

（1.浙江工业职业技术学院建筑工程学院，浙江绍兴，312000；2.浙江大学建筑工程学院，浙江杭州，310058）

风重耦合效应是指高耸结构侧向变形受到风和重力共同影响而引起结构静力和动力响应发生变化的现象。为了研究风重耦合效应的作用机理，利用结构几何非线性动力方程和等效线性随机振动理论求解。计算结果表明，重刚比是影响风重耦合效应最重要的参数，其值越大，结构振动固有频率越小，结构响应越大。当结构重刚比较小时，地面粗糙度、结构固有阻尼和平均风速对风重耦合效应影响不大。当重刚比较大时，风重耦合效应随结构固有阻尼和平均风速的增大而减小。

超高层建筑；风重耦合效应；风振；非线性振动

当今高耸结构发展迅速，给结构设计提出了很多新课题，其中一个是风重耦合效应（wind-gravity coupling effect，WGCE）。它指高耸结构在风荷载作用下产生横向位移，由于重力存在，加大了侧向弯矩，从而使横向位移进一步加大。这种现象的存在改变了结构的动力特性，使结构在脉动风作用下响应发生了变化。

当代的高耸结构由于自振频率小、高度高，风荷载的影响逐渐超过水平地震荷载已经成为结构主控水平荷载，而现行结构规范对此没有比较详尽的表述。高耸结构规范中对重力二阶效应给出了简单的附加弯矩计算法［1］，不能直接反映出结构动力特性的变化所产生的影响。此外在抗震设计中是否需要考虑重力二阶效应已经纳入结构设计规范［2⁃4］，但并没有给出随机荷载作用下的计算方法。

尽管《高程建筑混凝土结构技术规程》重力二阶效应的规定非特指地震荷载，对风荷载的问题却无特殊说明。工程实例表明重刚比较大的高耸结构必须计入风重耦合效应才能满足工程计算的要求［5⁃7］，事实上结构在重力的作用下动力作用下会产生许多新的特征。本文将对这一现象进行深入分析，利用随机振动理论在统计意义上分析风重耦合效应下顺风向结构振动中产生的现象。

1 高耸结构风重耦合计算方法

高耸结构可以简化为悬臂梁模型，设结构总高度为H，在沿高某处的水平位移为u，线密度为m，弯曲刚度为kb，由弯曲引起的转角为θ，水平风荷载为p，竖向压力为N。则结构的动力方程为

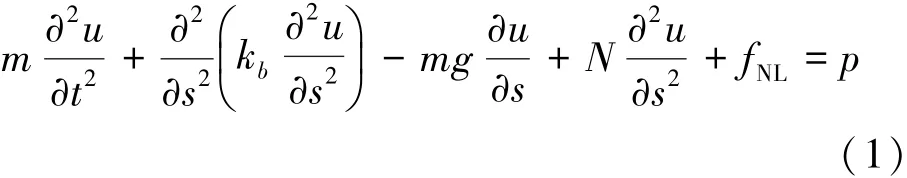
式中：fNL为非线性项。方程左边的第1项为惯性力项，第2项为结构抗力项，第3项是由于重力作用产生的线性附加项，第4项上部压力项，为第5项为非线性项，其中包含了重力作用高阶项。

方程（1）可以按平均风荷载响应和脉动风荷载响应进行分解，平均风荷载下的响应可以用非线性方程迭代求得。脉动风荷载作用下动力方程采用等效线性化，按照随机振动理论，求出振动响应值［8⁃11］，最后可以得到下式：

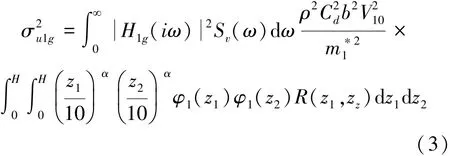
式中：z为建筑物某处高度，H1g传递函数，Sv为风速谱，Cd为高耸结构体型系数，b是迎风面宽度，V10为10 m处平均风速，R为相关系数，φ1为结构一阶模态。

2 风重耦合效应相关参数

本文研究的目的是分析风重耦合效应程度，为了有效表示风重耦合的大小，定义物理量变化系数：

式中：Wg为计入风重耦合效应的物理量，W0为不考虑风重耦合效应的物理量。

结构设计中重刚比是一个重要指标，它是反映高层结构的稳定性，对于上下均匀的结构可定义为结构的总重和高度平方的乘积与弯曲刚度之比：

式中：G为建筑物的总重，kb为结构的弯曲刚度。

3 参数对顺风向风重耦合效应影响

高耸结构的风重耦合效应与众多因素有关，风重耦合效应大小首先取决于结构刚度大小，因此与重刚比有最直接的关系。除此之外结构固有阻尼、与来流风特性以及地面粗超度都具有一定的关系。这里将对平均风荷载产生的变形、结构动力特性和结构响应一一进行分析。

3.1 平均风作用下位移的变化

在平均风荷载作用下，结构产生静力位移，因此平均风作用下的求解比脉动风作用下更为方便，方程（1）中去掉惯性项后用牛顿法即可求解。

本算例为上下均匀的高耸结构，主要参数如下：高耸结构质量刚度上下均匀，平面尺寸40 m×40 m，高度为300 m，单位长度重量2667 kN／m，地貌为B类地区，地面以上10 m处平均风速为20 m／s。

计算结果如图1所示。相同的静力荷载，不同结构重刚比条件下，考虑风重耦合效应的计算结果要大于未考虑风重耦合效应的结果，而且随着重刚比的增加，两者之间的差异逐渐扩大，也就是说随着变形增大结构刚度减弱，重力影响产生非线性变形会逐步增大。同时计算表明，一般高耸结构重刚比在现行规范规定范围内风重耦合致使结构变形增大效应呈线性变化。

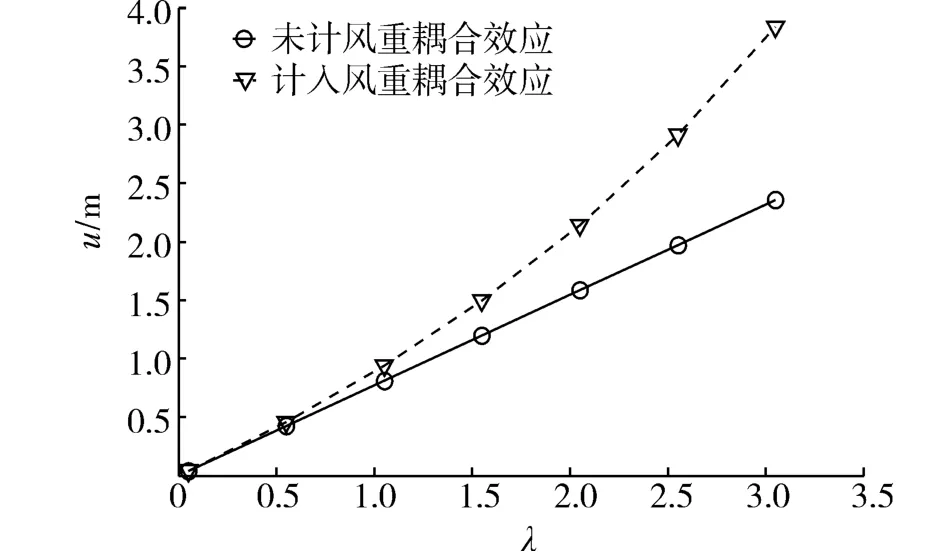
图1 不同重刚比下平均风荷载产生顶部位移变化Fig.1 Displacement on the top of the building acted by average wind load changing with gravity⁃rigidity ratio

3.2 结构体系基频的变化

在风重耦合作用下，结构的频率会发生变化，结构频率的变化和结构的重刚比密切相关。图2为脉动风荷载作用下基频对结构重刚比曲线图，算例的条件如前面，图中显示结构的基频随着重刚比增加逐步下降，但下降的趋势逐渐减缓。从图中可以看到计入风重耦合效应的曲线数值比常规计算的要小，这是因为重力存在相当于减小了结构的刚度。

图2 不同重刚比下等效结构基频的变化Fig.2 Natural fundamental frequency changing with gravity⁃rigidity ratio

进一步计算表明，由于风重耦合效应，结构的基频变化系数的绝对值随着重刚比增加而增长，并且呈线性增长。

3.3 结构脉动风响应的变化

位移响应影响的主要是传递函数，而传递函数和结构的重刚比、结构阻尼以及平均风荷载产生的位移有关。通过算例来分析结构的风重耦合效应，计算条件同前面算例，结构阻尼比为0.01。

图3为结构响应图，结构响应值随着重刚比而增加，计入风重耦合效应的曲线数值比常规计算的要大。并且随着重刚比增大2条曲线逐渐分开，即风重耦合效应随重刚比增大。图中可以看出在规范限定重刚比范围内，风重耦合效应引起计算结果差异是非常明显的。

图3 不同重刚比下结构响应的变化Fig.3 Responses of structures changing with gravity⁃ri⁃gidity ratio

表1是结构顶部位移响应变化系数随结构阻尼比和重刚比变化的数据。表格中间数据区有2条限位线，是现行结构规范对高层建筑重刚比设定的2个界限，第1条是设计时是否需要考虑重力二阶效应的界限，第2条是结构重刚比不容许大于的最低界限。表1中反映出结构固有阻尼对结构的振动起到了阻碍作用，当结构重刚比较小时阻尼抑制风重耦合效应不明显，而结构重刚比较大时阻尼的影响就较大。此外，在重刚比较大时，随着结构的固有阻尼系数的提高，风重耦合效应变化系数反而减小。

平均风速是引起结构风重耦合效应大小的另一个重要因素。表2计算条件同前面，结构的阻尼比为0.01，地面粗糙度为B类。从表中显示，当重刚比较大时，随着平均风速的增大，位移响应变化系数总体上呈减小趋势。结构响应变化系数反应了结构风重耦合效应的大小，响应变化系数减小也表明风重耦合效应的减弱。产生这种现象的原因是由于平均风荷载产生的位移存在，减小了风重耦合效应。

表1 不同重刚比和结构阻尼下位移响应变化系数Table 1 Variation coefficient of displacement with differ⁃ent damp ratio and gravity⁃rigidity ratios %

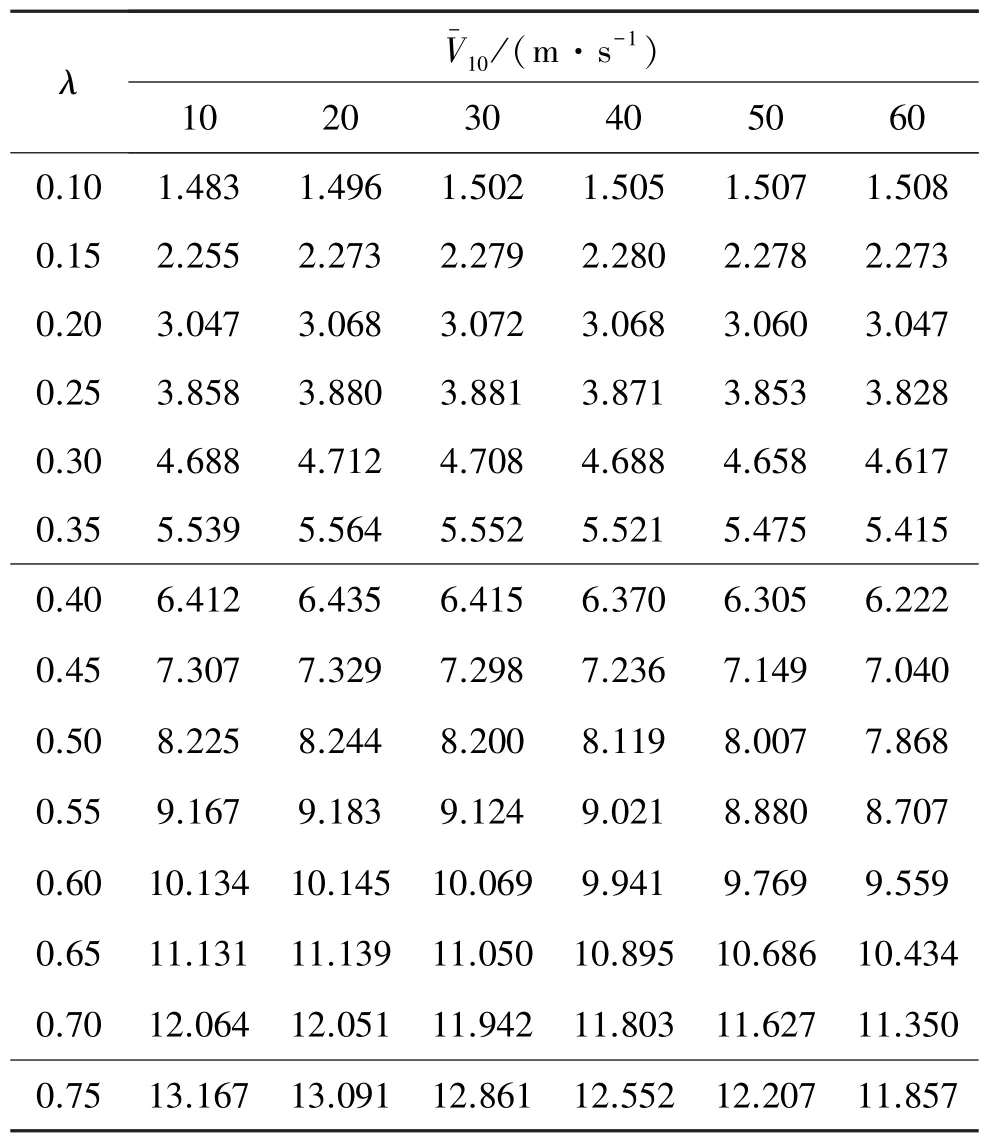
表2 不同重刚比和平均风速下位移响应变化系数Table 2 Variation coefficient of displacement with differ⁃ent average wind speed and gravity⁃rigidity ratios %

图4为不同平衡位置悬臂结构的振动受回复力情况，图中显示：当振动中心位置位于中间时，左右两边的重力刚好增大振动的幅值；但是当振动中心位置偏离中间时，振动到右边时重力增大振动的右幅值，振动到左边时重力却减小左边的幅值，由此导致脉动风作用下风重耦合效应的减小。

图4 振动中心位置变化时结构受重力情况Fig.4 The state of structure acted by gravity as center of vibration changing

最后要说明的是地面粗糙度对风重耦合效应也有影响，但计算表明影响程度不大，可以不做考虑。

4 结论

本文讨论了高耸结构风振时风重耦合效应的变化规律，计算了结构顺风向风振响应，从而得到顺风向风重效应的变化规律，得到以下结论：

1）风重耦合效应在平均风荷载作用下表现为重力使结构水平向变形增大，并且随着结构重刚比增大，其变形呈加速增大趋势。

2）风重耦合效应引起了结构刚度减小，从而使结构一阶固有频率比常规计算要小，一阶固有频率的变化系数与重刚比成正比。

3）由脉动风产生的结构的响应也是随着结构的重刚比增大而增大。结构的阻尼值和平均风速均对结构的风重耦合效应有一定的影响，尤其是重刚比较大时，结构的响应随着增大而减小。

［1］王肇民，马人乐.GB 50135-2006，高耸结构设计规范［S］.上海：中国计划出版社，2006.

［2］蔡益燕，胡庆昌，周炳章，等.JGJ 99-1998，高层民用建筑钢结构技术规程［S］.北京：中国建筑工业出版社，1998.

［3］徐培福，黄小坤，荣柏生，等.中华人民共和国住房和城乡建设部.GB50010⁃2010.建筑抗震设计规范［S］.北京：中国建筑科学研究院，2010.

［4］徐培福，黄小坤，荣柏生，等.中华人民共和国住房和城乡建设部.JGJ3⁃2010.高层建筑混凝土结构技术规程［S］.北京：中国建筑科学研究院，2010.

［5］陆天天，赵昕，丁洁民等.上海中心大厦结构整体稳定性分析及巨型柱计算长度研究［J］.建筑结构学报，2011，32（7）：8⁃14.LU Tiantian，ZHAO Xin，DING Jiemin，et al.Stability a⁃nalysis of the Shanghai tower and research on effective length of super column［J］.Journal of Building Structures，2011，32（7）：8⁃14.

［6］侯小美，宋宝东.复杂高层的整体稳定性分析［J］.结构工程师，2008，24（6）：51⁃56.HOU Xiaomei，SONG Baodong.Stability analysis for com⁃plex tall building［J］.Structural Engineers，2008，24（6）：51⁃56.

［7］马晓董，吴建华，何锦江，等.变截面单管塔考虑风荷载、重力-位移（P⁃Δ）二阶效应的半解析法［J］.制冷空调与电力机械，2008，29（3）：84⁃87.MA Xiaodong，WU Jianhua，HE Jinjiang，et al.Semi⁃ana⁃lytic method considering P⁃Δ effect for variable cross⁃section steel pole［J］.Refrigeration Air Conditioning and Power Ma⁃chinery，2008，29（3）：84⁃87.

［8］LUTES L D.Approximate technique for treating random vi⁃bration of hysteretic system［J］.The Journal of Acoustical Society of America，1970，48（1）：299⁃306.

［9］ZHU W Q，YU J S.The equivalent nonlinear system method［J］.Journal of Sound and Vibration，1989，129（3）：385⁃395.

［10］朱位秋，余金寿.预测非线性系统随机响应的等效非线性系统法［J］.固体力学学报，1989，10（1）：34⁃44.ZHU Weiqiu，YU Jinshou.Equivalent nonlinear system method for predicting response of nonlinear systems to ran⁃dom excitations［J］.Acta Mechanica Solida Sinica，1989，10（1）：34⁃44.

［11］CAI G Q，LIN Y K.A new approximate solution technique for randomly excited nonlinear oscillators［J］.International Journal of Non⁃Linear Mechanics，1988，23（5／6）：409⁃420.

Analysis of the downwind response of high⁃rise structures taking into account the wind⁃gravity coupling effect

ZHONG Zhenyu1，2，LOU Wenjuan2

（1.School of Civil Engineering and Architecture，Zhejiang Industry Polytechnic College，Shaoxing 312000，China；2.College of Civil Engineering and Architecture，Zhejiang University，Hangzhou 310058，China）

Wind⁃gravity coupling effect（WGCE）is a phenomenon that static and dynamic responses of high⁃rising structure acted by wind and gravity are changed.In order to study mechanism of WGCE，the method about nonlin⁃ear dynamic equation and equivalent linear random vibration theory is used to solve the problem.Calculated result indicates that gravity⁃rigidity ratio is an important parameter for WGCE.Natural frequency of structure decreases and response of structure increases with gravity⁃rigidity ratio of structure.Ground roughness，natural damping and average wind speed little impact on WGCE as value of gravity⁃rigidity ratio is small.While value of gravity⁃rigidity ratio is large，WGCE decreases with natural damping and average wind speed.

high⁃rising structure；wind⁃gravity coupling effect（WGCE）；wind vibration；non⁃linear vibration

10.3969／j.issn.1006⁃7043.201402017

TU312

：A

：1006⁃7043（2015）06⁃0765⁃04

http：／／www.cnki.net／kcms／detail／23.1390.u.20150428.0854.007.html

2014⁃02⁃14.网络出版时间：2015⁃04⁃28.

国家自然科学基金资助项目（51378468）.

钟振宇（1970⁃），男，教授；楼文娟（1963⁃），女，教授，博，博士生导师.

楼文娟，E⁃mail：louwj＠zju.edu.cn.