一种改进迭代误差分析端元提取算法

赵春晖，崔士玲，赵艮平，钟卫

（哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001）

一种改进迭代误差分析端元提取算法

赵春晖，崔士玲，赵艮平，钟卫

（哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001）

迭代误差分析（IEA）算法是应用比较广泛的端元提取算法之一，针对IEA端元提取算法计算量大的缺点，从减少参与迭代过程中的像元数目进行改进。根据凸面几何理论，混合像元位于其端元构成子空间内部，这部分像元到其端元正交子空间（OSP）投影值理论上为零，在迭代求下一个端元过程中，可以将这部分无用像元去除，从而减少每步迭代过程像元数目。采用模拟数据和真实高光谱数据进行实验，证明改进算法与原算法提取端元精度相同，随着端元提取个数的增多，参与迭代过程的像元数目逐次减少，比原始的IEA端元提取算法减少了计算时间。

端元提取；迭代误差分析；正交子空间投影；最小二乘算法

近年来，高光谱遥感技术快速发展［1］。目前，高光谱遥感已经在农业生产、环境监测、地质勘探、军事对抗等多个领域得到成功应用［2］。由于地面的复杂多样性及传感器空间分辨率的限制，导致混合像元在高光谱图像上广泛存在［3］。因此，如何有效地解决混合像元是高光谱图像分析的难题之一。

在混合像元分解中，端元提取是关键。自动端元提取是高光谱图像端元提取面临的一大挑战，在过去的几十年里已经提出了很多端元提取算法。有代表性的方法包括像素纯度指数（PPI）［4］、光学实时自适应光谱识别系统（ORASIS）［5］、迭代误差分析（IEA）［6］、内部最大体积（N⁃FINDR）［7］和自动形态学端元提取（AMEE）［8］，等。IEA是一种不需要对原始数据进行降维或者去冗余而直接对数据处理的端元提取算法，以误差大小作为判断端元的标准［3］。已经证明IEA端元提取算法是具有较好鲁棒性的广泛应用的端元提取算法之一。由于IEA是顺序迭代求取每个端元，随着端元数目的增大，它的计算量也随之增大。在迭代的过程中，并不是所有的混合像元都对端元的提取有帮助。针对此问题，本文在深入分析最小二乘算法与正交子空间投影之间关系的基础上，发现由已经提取端元构成凸面单形体内部的像元到已提取端元构成的正交子空间的投影理论上为零，这部分像元对下一个端元提取无用，可以剔除，以此降低每步迭代计算量。

1 迭代误差分析算法

迭代误差分析（iterative error analysis，IEA）以线性光谱混合模型的代数学描述为基础，是一种不需要对原始数据进行降维或者去冗余而直接对数据处理的端元提取算法，以误差大小作为判断端元的标准［3］。线性光谱混合模型［9］可以表示为

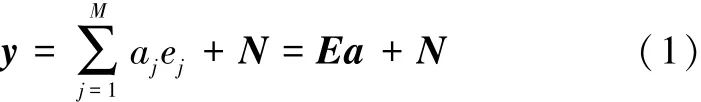
式中：y为混合像元，E是端元，a是混合系数，M是端元的数量，N表示噪声影响。

该模型有2个约束条件：

1）aj≥0非负约束；

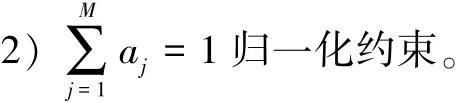
迭代误差分析端元［3］提取算法首先给定一个初始向量，然后采用全约束最小二乘方法对混合像元y进行解混，每次解混操作得到式（1）的一个估计a＾，利用已有的端元E和a＾可得到y的一个估计y＾，那么误差可表示为

对应的y'为误差向量，产生最长误差向量的像元记为新的端元，加入端元集合并开始下一次迭代，直到找到M个端元或误差向量长度足够小。需要注意的是，初始向量只参与第1个端元的选择，得到第1个端元后，初始向量不再参加后面端元提取的运算。

有时，为了减小噪声和误差，在每次迭代中允许选择误差向量最长且光谱角足够小的若干像元取平均值，得到新的端元。

2 改进的IEA端元提取算法

由第1部分IEA端元提取算法可以看出，最耗时的部分在于每次迭代过程误差向量模值的计算，如果能够减少每次迭代过程中的像元数目，那么计算量就可以降下来。误差计算过程与正交子空间投影之间存在如下联系：

式中：I为与PE同阶的单位矩阵，为端元E的正交子空间。

对于传统线性光谱混合模型，y可以表示成不感兴趣部分（已经提出端元以及由它们构成的混合像元）与感兴趣部分（剔除不感兴趣剩余的部分）的混合：

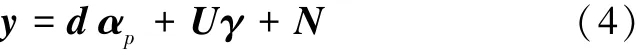
式中：d为感兴趣部分，αp为d所对应的丰度，U为不感兴趣部分，γ为U所对应的丰度，N为噪声。

通过均方根误差的计算式（3）可以分为2部分计算，先计算前一部分yTP⊥E，然后再和混合像元y相乘，求最大值得到端元。假如已经提取出m个端元EM＝(e1，e2，…eM)，构造它们的正交子空间：

由式（7）可以看出，经过将混合像元投影到已提取端元正交子空间上，背景信号（由已提取端元构成凸面单形体内部的混合像元）被消除，原始噪声也得到了投影压缩。

为了更直观的说明去除像元的过程，用提取出3个端元的几何关系为例进行说明，如图1所示，3个实黑点代表已提取的3个端元e1、e2和e3，其中圆圈代表由e1、e2和e3构成单形体内部混合像元，方形代表其他像元，圆圈代表的像元到端元e1、e2和e3正交子空间的投影为零，可以在下一步迭代过程中去掉，新的端元来源于方形代表的像元。

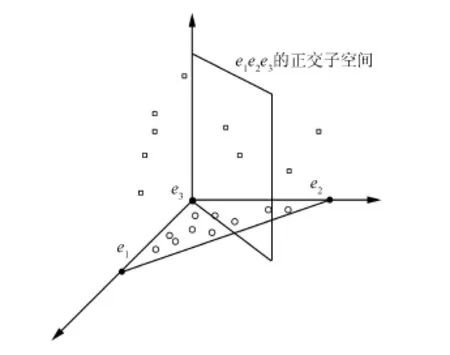
图1 3个端元混合像元去除示意图Fig.1 Mixture of three endmembers illustrating the pixels removal

改进IEA端元提取算法步骤：

1）给定一个初始向量（第1个初始端元选择的是距离原点最远的若干像元的均值），并且确定端元个数；

2）用得到的E计算均方根误差，对图像数据中每个向量通过式（3）求取均方根误差，得到误差矩阵；

3）选择误差矩阵中模值最大的点，为了减少噪声和误差，在每次迭代的过程中选择误差向量最长且光谱角足够小的若干个像元取平均值，将得到的平均值作为第1个端元e1；

4）求端元e1的正交子空间，将所有的像元投影到e1的正交子空间上，将投影值小于阈值ε的像元去掉，得到新的观测值为y1；

5）用e1对y1中每个向量通过式（3）求取均方根误差，为了提高端元提取的准确性，可以选择全约束最小二乘算法对丰度进行估计，将误差最大且光谱角足够小的若干个像元取平均值作为第2个端元e2；

重复上面步骤，直至找到规定数量的端元为止。

3 仿真实验

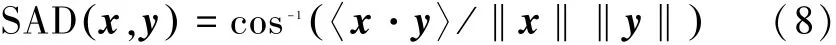
式中：〈x·y〉是2个向量x和y的内积。

3.1 模拟数据实验

仿真高光谱数据，从美国地质调查局（USGS）矿物光谱库选取8种地物光谱，分别为明矾石、铵长石、方解石、高岭石、白云母、榍石、黄钾铁矾和绿脱石，用这8种地物合成40 000个具有224波段的高光谱数据，每个像元由8种纯端元中的若干种随机混合而成，并添加8种地物的纯光谱，共40 008个像元，为模拟真

IEA端元提取算法是经典的端元提取算法之一，在文献［10⁃11］已经和其他端元提取算法进行了比较，本文对改进的算法与原始的IEA算法进行对比。为了验证改进算法的有效性，分别用合成模拟数据和真实的高光谱数据进行实验。计算机的硬件配置为：处理器为Intel Core i3，主频为2.13 GHz，内存为DDR32 GB，仿真软件为Matlab 7.11版本。

为了评价端元提取的精度，采用光谱角距离作为评价指标，光谱角距离［12］定义为实的高光谱影像，附加信噪比为25 dB的高斯噪声。

为了验证算法的有效性，做2组实验，第1组实验验证改进算法提取端元光谱与原始算法提取端元相同，并且精度相同，说明去除部分无用像元并不影响端元提取的精度；第2组实验验证在保证端元提取精度前提下，改进算法随着端元提取个数的增多，在每次迭代过程中减少的像元数目和减少像元百分比与投影阈值之间的关系以及改进算法比IEA算法减少的时间。

改进算法和原始算法都能够准确的提取出8种端元，为了更客观的评价提取出端元的准确度，表1给出改进算法与原始算法端元提取精度对比，可以看到，光谱角都很小，提取出的效果很好，并且2种算法提取出端元的精度相同，说明改进的算法并不影响端元提取的精度。

表2是在保证端元提取精度基础上，不同阈值下的每步迭代减少的像元个数及占总像元的百分比。横向来看，随着提取端元个数的增多，每步减少的像元数目逐次增多，在阈值设置从0.016～0.02时，第7次迭代减少的像元数目达到90%以上，证明该算法能够大大减少运算量。纵向来看，随着投影阈值的变化，每步迭代减少的像元数目是不同的，当阈值为0.020时，达到理想的效果，计算时间比较小。合理设置投影阈值对计算量降低十分关键。

表1 改进算法与原始IEA提取端元的精度对比Table1 Comparing the precision of improved endmember extraction algorithm with the original IEA

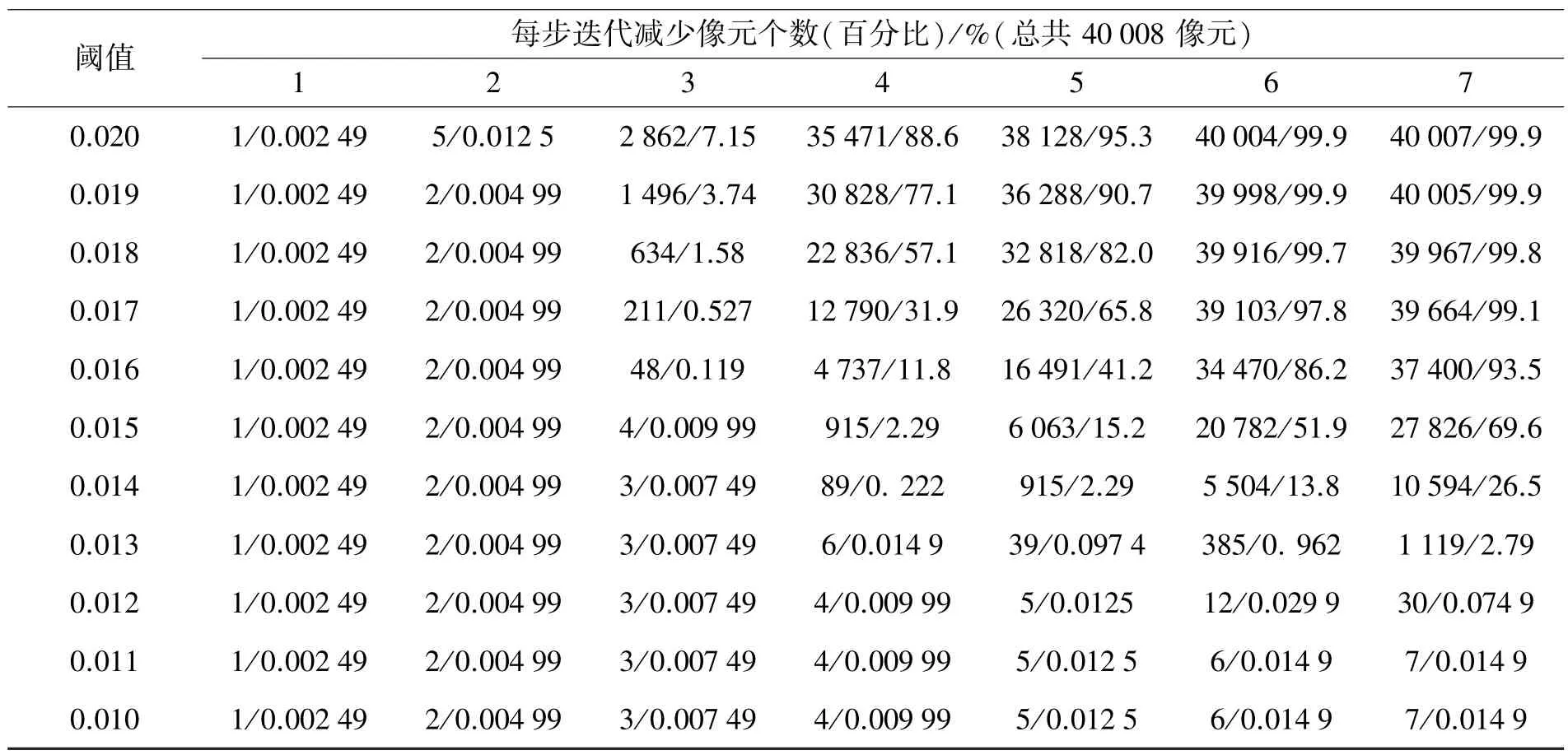
表2 不同阈值下的每步迭代减少的像元个数及占总像元的百分比Table 2 The number of removal pixels and the percent of total pixels per iteration under different thresholds

表3是改进算法在不同阈值下与原始IEA算法运行20次平均时间对比，改进算法随着投影阈值的增大，计算时间逐步降低，当阈值为0.02时，比原始算法计算时间降低了约50%，大大减小了计算时间，但是当阈值降低到0.012时，计算速度反而比原来还要慢，原因在于每次迭代减少的像元数目急速减少，而阈值的判定也需要花费时间，因此合理有效地设置阈值可以比原始IEA大大降低计算时间。

表3 不同阈值下改进算法与原始IEA算法运行20次平均时间对比Table3 Average time comparison of improved algorithm with the original IEA algorithm running 20 times under different thresholds s

3.2 真实高光谱数据实验

真实的高光谱数据采用Cuprite矿物数据，该影像由AVIRIS传感器获得，而且含有该地区对应的地质调查图。实验所用数据大小为250×191像元，光谱范围为0.369～2.480 μm，共224波段，去除因水汽吸收和传感器噪声等低信噪比波段（1～2、104～113、148～167、221～224），实验用的数据共188波段。

从Cuprite矿物数据中提取出6种端元，分别为沙漠地表、玉髓、绿脱石、明矾石、榍石和蒙脱石，提取出的端元在文献［13］中可以查到。由模拟实验得出：设置合理的阈值可以在保证提取精度的基础上，最大限度减少计算量。在真实数据中设置的阈值为0.002，在此阈值下可以获得良好的效果，提取6种端元，总共迭代5步，在保证端元提取精度的前提下，每次迭代中减少的端元数目与所占的百分比如表4所示，可以看出，随着端元提取个数的增多，每次迭代减少的像元数逐次下降。改进算法与原始算法提取出的端元光谱相同，将提取出的端元光谱与USGS光谱库进行对比，如图2所示。

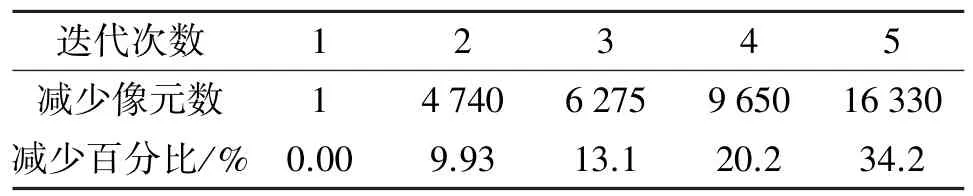
表4 每步迭代减少的像元个数及占总像元的百分比Table4The number of removal pixels and the per⁃cent of total pixels per iteration

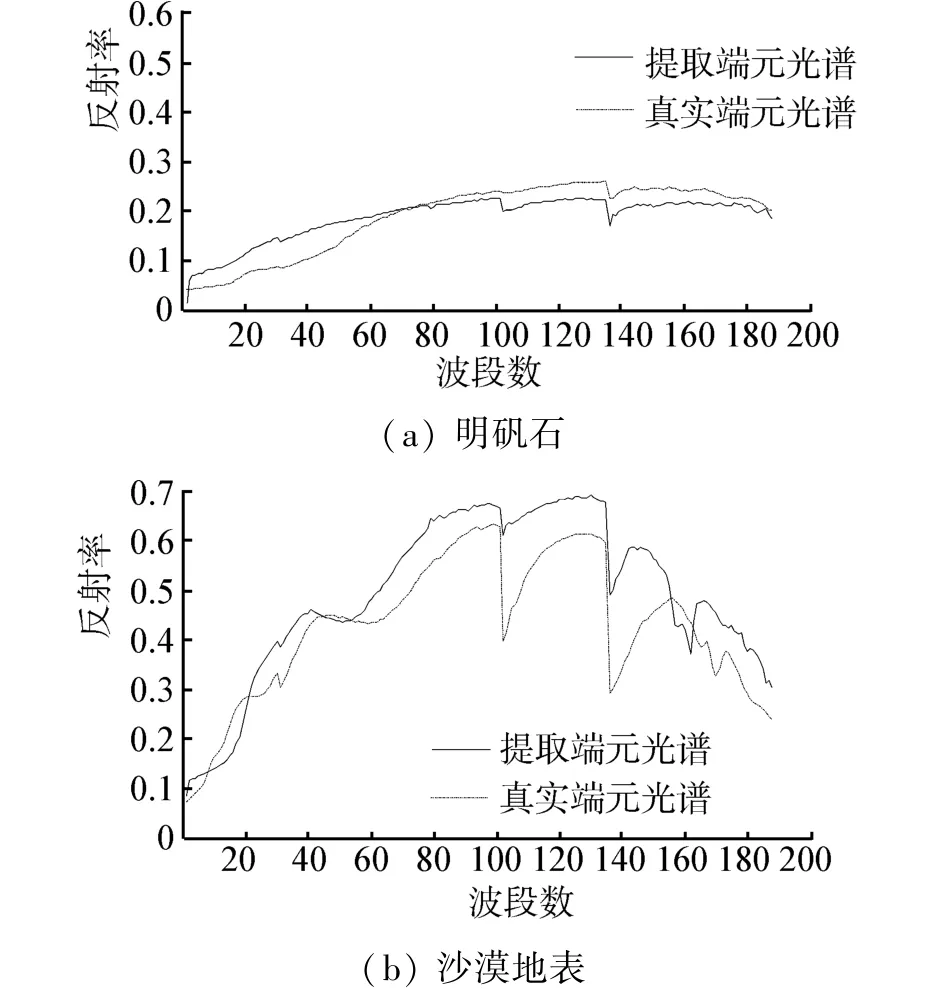
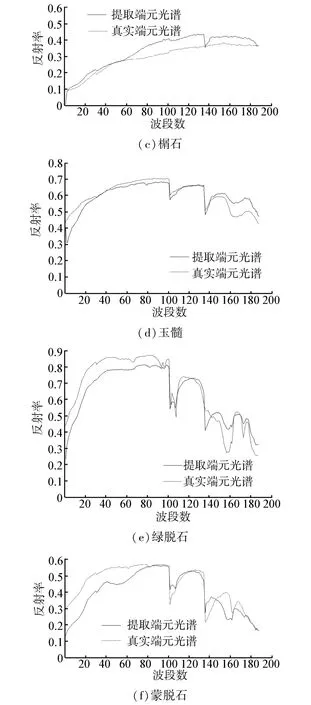
图2 提取端元光谱与真实光谱对比Fig.2 Extraction endmember spectral compared with the real spectral

从图中可以看出，提取出的端元光谱和真实光谱基本吻合。为了更客观地评价提取端元结果的精确性，采用光谱角距离进行评价，光谱角越小，精度越高，如表5所示，可以看出改进算法与原始IEA端元提取算法提取端元精度相同，但是改进算法所用的时间明显减少，表5最后一行给出的是运行20次的平均时间，改进算法所用时间比原始算法大约减少了25%。

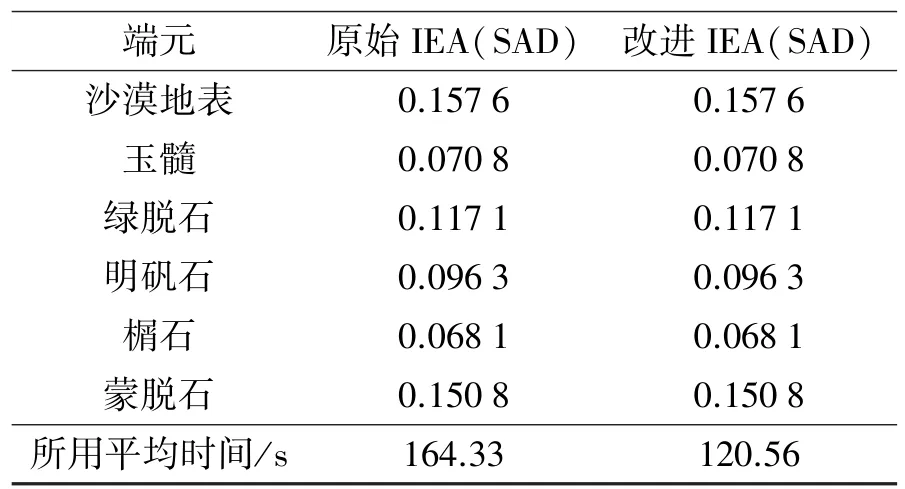
表5 改进算法与原始IEA提取端元的精度及时间对比Table5 Comparing the precision and time of im⁃provedendmemberextractionalgorithm with the original IEA

4 结束语

本文提出了一种改进的IEA端元提取算法，通过将像元到已提取端元正交子空间投影值，去除已提取端元构成单形体内部的像元，从而减少每次迭代过程中像元的个数，提高了算法的效率。实验结果证明，改进算法在保证端元提取精度的基础上，大大减少了参与每次迭代的像元数目，整体计算时间降低。由于噪声等的影响，投影阈值的设定需要根据实际情况设定，如何自动的选择阈值是下一步研究的主要问题。

［1］王立国，魏芳洁.结合遗传算法和蚁群算法的高光谱图像波段选择［J］.中国图象图形学报，2013，18（2）：235⁃242.

WANG Liguo，WEI Fangjie.Band selection for hyperspectral imagery based on combination of genetic algorithm and ant colony algorithm［J］.Journal of Image and Graphics，2013，18（2）：235⁃242.

［2］王立国，赵春晖.高光谱图像处理技术［M］.北京：国防工业出版社，2013：18⁃29.

［3］张兵，高连如.高光谱图像分类与目标探测［M］.北京：科学出版社，2011：30⁃55.

［4］BOARDMAN J W.Automating spectral unmixing of AVIRIS data using convex geometry concepts［J］.Summaries of the Fourth Annual JPL Airborne Geoscience Workshop，JPL Publication，1993，1：11⁃14.

［5］BOWLES J，ANTONIADES J，BAUMBACK M，et al.Real time analysis of hyperspectral data sets using NRL's ORASIS algorithm［J］.Proceedings of the SPIE，1997，3118：38⁃45.［6］NEVILLE R A，STAENZ K，SZEREDI T，et al.Automatic endmember extraction from hyperspectral data for mineral ex⁃ploration［C］／／Proceedings 21st Canadian Symposium Re⁃mote Sensing，Ottawa，Canada，1999：21⁃24.

［7］赵春晖，成宝芝，杨伟超.利用约束非负矩阵分解的高光谱解混算法［J］.哈尔滨工程大学学报，2012，33（3）：377⁃382.

ZHAO Chunhui，CHENG Baozhi，YANG Weichao.Algo⁃rithm for hyperspectral unmixing using constrained nonnega⁃tive matrix factorization［J］.Journal of Harbin Engineering University，2012，33（3）：377⁃382.

［8］PLAZA A，MARTINEZ P，PEREZ R，et al.Spatial／spec⁃tral endmember extraction by multidimensional morphological operations［J］.IEEE Transactions on Geoscience and Re⁃mote Sensing，2002，40：2025⁃2041.

［9］王玉磊，赵春晖，齐滨.基于光谱相似度量的高光谱图像异常检测算法［J］.吉林大学学报：工学版，2013，43：148⁃153.

WANG Yulei，ZHAO Chunhui，QI Bin.Hyperspectral anom⁃aly detection algorithm based on spectral similarity scale［J］.Journal of Jilin University：Engineering and Technology Edi⁃tion，2013，43：148⁃153.

［10］PLAZA A，MARTINEZ P，PEREZ R，et al.A quantitative and comparative analysis of endmember extraction algo⁃rithms from hyperspectral data［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42：650⁃663.

［11］WINTER M E，WINTER E M.Comparison of approaches for determining end⁃members in hyperspectral data［J］.Proceedings IEEE Aerospace Conference.Big Sky，USA，2000，3：18⁃25.

［12］丁海勇，史文中.利用卡方分布改进N⁃FINDR端元提取算法［J］.遥感学报，2013，17（1）：130⁃137.

DING Haiyong，SHI Wenzhong.Fast N⁃FINDR algorithm for endmember extraction based on Chi⁃square distribution［J］.Journal of Remote Sensing，2013，17（1）：130⁃137.

［13］JOSÉ M P，JOSÉ M N，BIOUCAS D.Vertex component a⁃nalysis：a fast algorithm to unmix hyperspectral data［J］.IEEE Transactions on Geoscience and Remote Sensing，2005，43：898⁃910.

Endmember extraction algorithm based on improved iterative error analysis

ZHAO Chunhui，CUI Shiling，ZHAO Genping，ZHONG Wei
（College of Information and Communications Engineering，Harbin Engineering University，Harbin 150001，China）

Iterative error analysis（IEA）algorithm is one of the widely used endmember extraction algorithms.As for the compute-intensive shortcoming，this paper improves it from reducing the number of pixels participated in the iterative process.According to the convex geometry theory，mixed pixel locates on its internal subspace constituted by its endmembers.The projection value of these cells to their endmember orthogonal subspace（OSP）is zero，which can be removed during the iterative process for deriving the next endmember，thereby reducing the number of pixels in every iteration step.The experiments with simulated data and real hyperspectral data were done，proving that the improved algorithm has the same precision of the extracted endmember with original algorithm，and with the increasing of the number of extracted endmembers，the number of pixels participated in the iteration decreases grad⁃ually，which reduces the computation time than the endmember extraction of the original IEA algorithm.

endmember extraction；iterative error analysis；orthogonal subspace projection；least⁃squares algorithm

10.3969／j.issn.1006⁃7043.201310094

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006⁃7043.201310094.html

TP751.1

A

1006⁃7043（2015）02⁃0257⁃05

2013⁃10⁃31.网络出版时间：2014⁃11⁃27.

国家自然科学基金资助项目（61405041，61275010），黑龙江省自然科学基金重点资助项目（ZD201216），哈尔滨市优秀学科带头人基金资助项目（RC2013XK009003）.

赵春晖（1965⁃），男，教授，博士生导师.

赵春晖，E⁃mail：zhaochunhui＠hrbeu.edu.cn