两种不同通道内周期性充分发展流动换热的模拟研究

李 凌, 主苏苏, 刘建国

(1.上海理工大学能源与动力工程学院,上海 200093;2.华能太仓电厂,太仓 215424)

两种不同通道内周期性充分发展流动换热的模拟研究

李 凌1, 主苏苏1, 刘建国2

(1.上海理工大学能源与动力工程学院,上海 200093;2.华能太仓电厂,太仓 215424)

周期性直肋通道是从不同型式的高效换热器中抽象出来的通道模型,采用非稳态数学模型,应用周期性充分发展的假设模拟了周期性矩形直肋通道(A)和半圆形直肋通道(B)内的流动换热情况,并对两种通道的换热特性及其所表现出来的非线性特性进行了对比.计算时采用低雷诺数Re、二维、层流强制对流模型.结果表明,当Re较小时,流动与换热处于稳态;当Re大于某一临界值时,流动与换热发生了非稳态振荡,系统均表现出丰富的非线性现象.在计算范围内,A通道随着Re的增大经历了稳态与周期性振荡阶段;B通道则先后经历了稳态、周期性振荡、拟周期振荡以及混沌状态.

数值模拟;流动换热;直肋形状;周期性通道;非线性特性

Key words:numerical simulation;fluid flow and heat transfer;straight rib shape; periodical channel;nonlinear characteristics

近年来,周期性通道因其广泛的工程应用而受到越来越多的关注,如波纹板通道、矩形槽通道、锯齿形通道等.对于周期性通道内的流动与换热已有较多的研究成果[1-2].近期的研究表明,周期性通道内流体的流动换热过程因为周期性的干扰而呈现出振荡等非线性特性.汪健生等应用数值模拟方法分析了以周期性方式布置不同结构通道内产生的周期性自振荡流动现象,并研究了自激振荡流对下壁面物块传热特性的影响[3].卢玫等对锯齿形周期性通道内流动与换热的振荡等特性进行了探讨[4].许多学者针对流动与换热过程中出现的非线性现象进行了大量研究,但主要是针对自然对流,如封闭圆内开缝圆自然对流的非线性特性[5]、具有对称结构的封闭方腔内竖直板自然对流换热过程中的非线性现象[6]等.本文采用强制对流模型,对周期性矩形直肋通道和半圆形直肋通道内的流动换热特性进行了模拟研究,重点对两种通道中流动与换热的非线性特性进行了讨论.

1 物理模型与数值方法

A,B为两种几何结构不同的二维周期性通道(A通道肋片形状为矩形,B通道肋片形状为半圆形),如图1所示.通道取相同几何尺寸,a为肋片高度,两种通道肋片的位置及宽度和高度均相等.

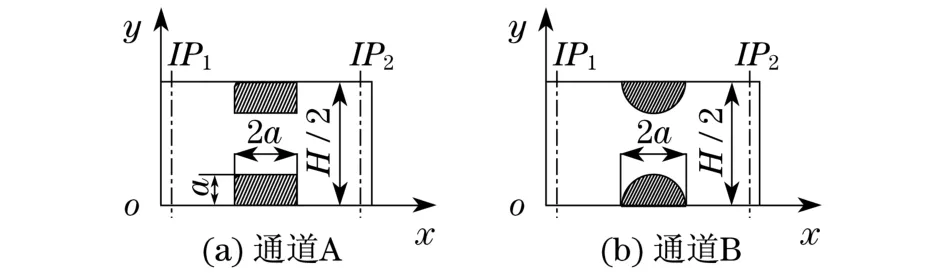
图1 A,B两种不同结构的周期性通道示意图Fig.1 Two different structures of periodic channel A and B

如图1所示的直角坐标系中,x方向取为流体主流方向,y方向与其垂直.IP1为距出口水平距离为一个几何周期的界面,IP2为距入口水平距离为一个几何周期的界面.根据水力当量直径的定义,选取两倍入口界面的高度H为无量纲参考长度,选取来流的平均速度U0为无量纲参考速度,即无量纲定义为

式中,x,y为有量纲坐标量;u,v分别为速度在x, y方向的分量.

假设流体不可压缩、无耗散,计算采用二维层流常物性强制对流模型,其无量纲化的控制微分方程组为

式中,U,V分别是x方向和y方向无量纲速度分量;P为无量纲压力;T为流体温度;TW为壁面温度;θ为过余温度,θ=T-TW;F为无量纲时间变量.本文选用空气为工作流体,普朗特数Pr=0.7,雷诺数Re和平均努塞尔数Nua分别定义为

式中,ν为流体动力黏度;θ1,θ2分别为通道入口和出口截面处的流体过余温度;A为不带肋片的通道单侧平板面积;Δtm为流体进出口过余温度的对数平均温差.

式(4)定义的平均努塞尔数Nua忽略了流体沿流动主流方向的导热.模拟采用周期性边界条件,并且采用扩大区域法来实现,即计算区域为一个几何周期并向两边各延伸两个网格,同时周期性进出口边界条件通过相互替代方法来实施.已有较多学者就肋片的几何尺寸对流动与换热的影响作过研究[7-8],而本文主要讨论不同直肋形状对流动换热特性的影响,所以,通道的长度、宽度及肋片的宽度、高度均取一固定值.计算区域无量纲长度为2.05,高度为0.5,直肋的最大宽度为0.25,最大高度为0.125.由周期性边界条件可以得到

式中,L1代表x方向上最后一个节点所在位置; IP1与IP2是为采用相互替代方法实施周期性进出口条件而引入;Θ为无量纲温度.

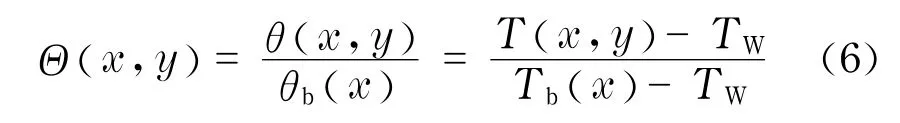
式中,θ(x,y),T(x,y)分别为坐标(x,y)位置处流体的过余温度和有量纲温度项;θb(x)代表截面流体平均过余温度;t为温度;Tb(x)为截面流体平均温度,定义为

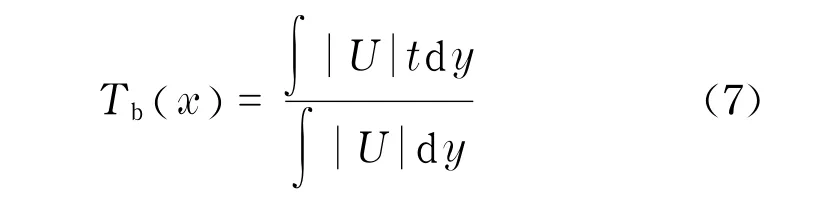
计算时采用了整体法,直肋部分附加了以下条件:U=0,V=0,θ=0,导热系数λ取一大数.利用有限容积法对上述控制方程组进行离散,对流项的离散选用具有三阶精度的QUICK[9]格式,压力与速度的耦合则采用SIMPLE算法.

对于周期性通道,已有诸多研究[10]表明,在一定的参数范围内,其通道内的流动与换热是随时间发生改变的,所以,对该问题采用非稳态模型进行模拟.无量纲时间步长取为0.005,计算的初始条件为

2 结果与讨论

首先对算法和网格数进行验证,最终选取的网格数为166×42,在此基础上模拟了Re=100,200,300, 385,400,440,600,700,800,1 000的工况.模拟结果显示,随着Re的增大,A,B两种通道中的流动换热均表现出了丰富的非线性特性.选取(84,22)为监测点,对两种通道中所呈现的振荡等非线性现象进行阐述.

2.1 A通道中流动与换热的非线性特性分析

图2为A通道中不同Re时平均努塞尔数Nua随无量纲时间F的变化曲线,图3(见下页)为相应工况下A通道中监测点的UV相图,即速度运动轨迹.

Re=200时,A通道中平均努塞尔数Nua经过一定时间的迭代之后趋于稳定,不再随时间变化,且对应工况下监测点的UV相图经过一定时间之后最终趋于一点,说明系统处于稳态.同样,利用数值逼近法进行多次模拟,得出稳态的临界雷诺数Recr= 385.在本文给定的条件下,当Re≥385时,流动和换热进入非稳态阶段.当Re=385时,Nua的分布规律呈现周期性振荡变化,且振幅基本一致,其相应工况下监测点的UV相图经过若干次迭代后形成一个闭合的曲线,即监测点U,V值周期性循环变化.此种状态下,系统处于周期性振荡阶段.模拟发现,在Re≤1 000范围内,随着Re的增大,A通道内的流动换热依然会呈现周期性振荡特性,且振荡幅度逐渐增大,相应监测点U,V值的变化幅值亦增大.

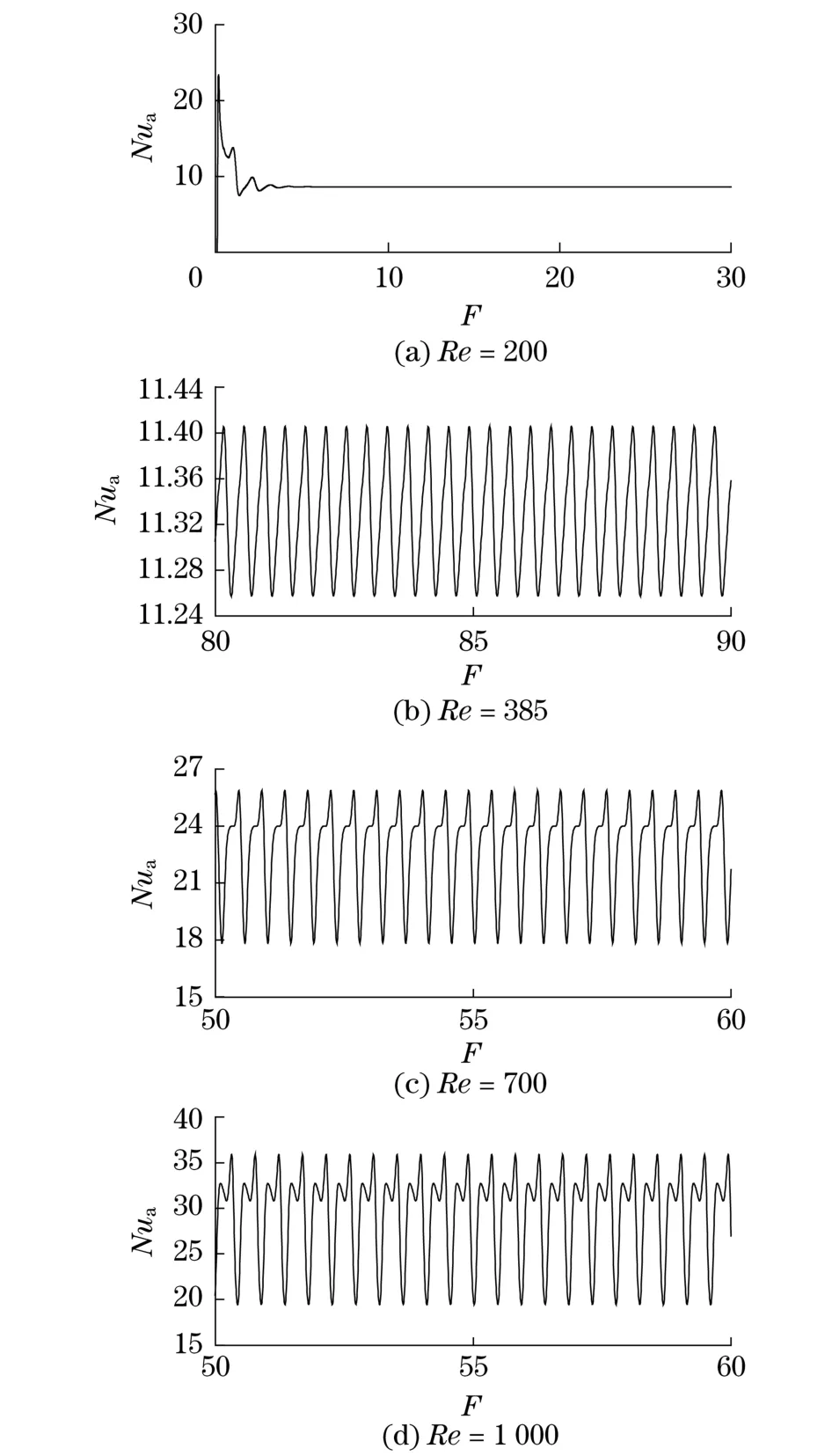
图2 A通道中不同Re时Nua随时间的变化曲线Fig.2 Curve of Nuachange with time under different Re in channel A

2.2 B通道中流动与换热的非线性特性分析

图3 A通道中不同Re时监测点的UV相图Fig.3 UV phase diagram of the selected monitoring point under different Re in channel A

图4(见下页)为B通道中不同Re工况下,平均努塞尔数Nua随无量纲时间F的变化曲线,图5为B通道中所取监测点在相应工况下的UV相图.观察发现,Re=200时,B通道也处于稳态.同样,利用数值逼近法进行多次计算,得出在Re增大到440时,系统过渡为非稳态.由此可见,A通道的稳态临界雷诺数Recr小于B通道的,即同样条件下A通道更早地进入非稳态状态.这是因为矩形直肋相比半圆形直肋对流体流动的扰动更大,对流动边界层的破坏更为剧烈.B通道在Re=440时,图中Nua的分布规律及监测点的相图表明此时系统处于周期性振荡状态.研究发现,在Re＜700的范围内,系统一直处于周期性振荡阶段,且振荡随着Re的增大逐渐加剧.Re=700时,Nua随无量纲时间F的迭代曲线具有多个波峰,较Re=440时整体振荡幅度明显增大,基本呈周期性,但波动幅值大小不一,其相应工况下监测点的UV相图由多簇互不相交却又无限靠近的封闭曲线组成,线簇间的偏离程度正比于Re的大小.此种状态下,系统已进入拟周期振荡阶段.当Re=1 000时,Nua随时间的振荡曲线呈现出强烈的非周期性振荡现象,流动与换热表现出较强的非线性特性,其相应工况下监测点的UV相图也变得杂乱无章,系统进入混沌状态.

图4 B通道中不同Re时Nua随时间的变化曲线Fig.4 Curve of Nuachange with time at different Re in channel B

2.3 不同Re下A,B两种通道中系统所处状态的比较

表1为不同Re下A,B两种通道系统所处状态的比较,其中,s代表稳态(steady),up代表非稳态周期性振荡(unsteady periodical oscillation),qp代表拟周期振荡(quasi-periodic oscillation),uc代表混沌(unsteady chaotic oscillation).对于本文所研究的通道,当Re＜385时,A,B两种通道内的流动与换热均是稳态的;当Re=385时,A通道过渡为非稳态周期性振荡,B通道仍然处于稳态;当Re增至440时,B通道也进入非稳态周期性振荡;当Re= 700时,B通道进入拟周期振荡阶段;随后Re增至1 000时,系统发展成为混沌状态.而A通道在Re=400～1 000范围内,系统始终处于周期性振荡状态.对比发现,A通道较B通道更早地进入非稳态阶段,且在较大Re范围内始终维持着周期性振荡状态,而B通道更容易从一种状态过渡到另一种状态.作者认为这与直肋的几何形状相关,矩形直肋较半圆形直肋对流体流动的扰动更为剧烈,振荡更明显(见图2和图4),所以,A通道更早进入非稳态.半圆形直肋相比矩形直肋对流体的“滞止”能力较弱,其圆弧对流体流动具有“光滑过渡”作用,因而对流场的扰动便不像矩形直肋那样强烈,也正因为如此,所以对流场的改变更为敏感,一旦流速增大,更容易从一种状态过渡到另一种状态.

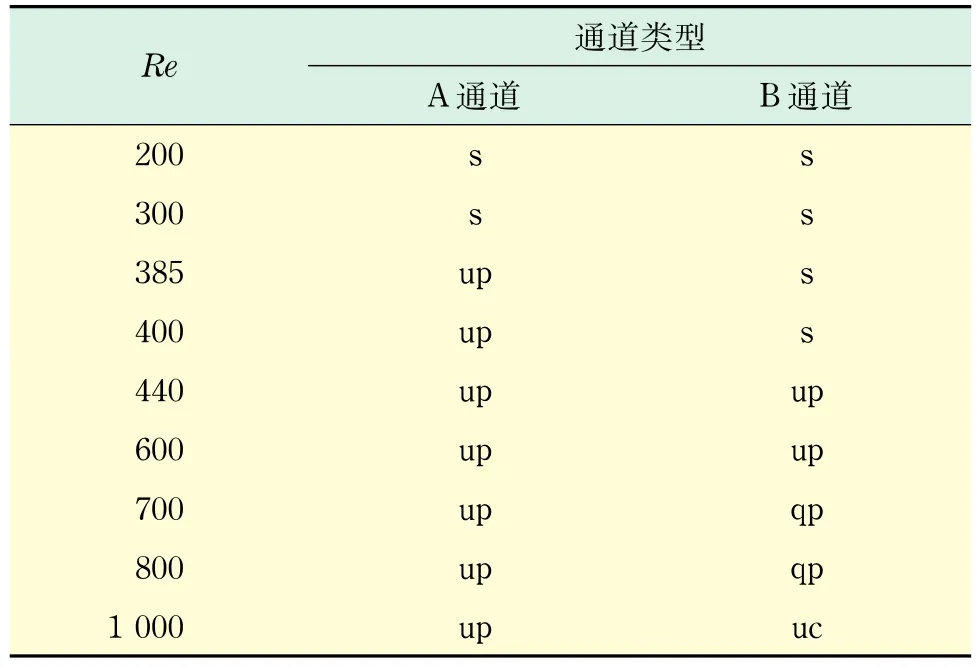
表1 不同Re数下A,B两种通道系统所处状态的比较Tab.1 Comparation of the status in channel A and channel B under different Re numbers

2.4 A,B通道的换热特性对比

研究表明,在Re较小时,A,B两种通道均具有稳态解,当Re增大到一定值时,流场和温度场呈现出周期性振荡现象.因此,在对比时,对Nu作时均化处理,即按时间进行加权平均.在一个振荡周期上的时均努塞尔数Nuavg按式(9)计算,表2给出了不同Re时A,B通道中Nuavg的数值.

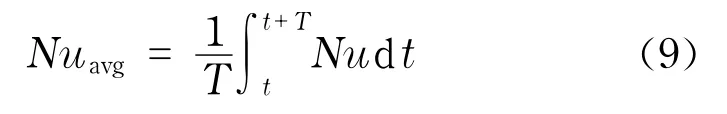
由表2可见,相同Re时,A通道的时均努塞尔数Nuavg大于B通道的,说明在一定条件下,A通道的结构类型更有利于促进强化换热.同一种类型的通道中,随着Re的增大,流动换热的Nuavg整体呈逐渐增大的趋势,进而也说明振荡有利于换热.

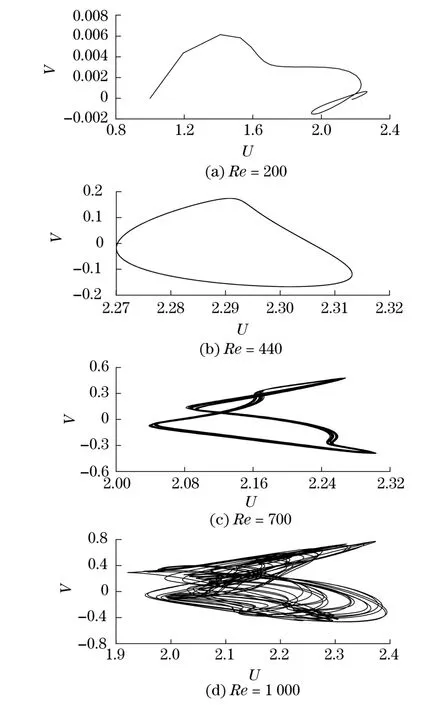
图5 B通道中不同Re时监测点的UV相图Fig.5 UV phase diagram of the selected monitoring point at different Re in channel B

表2 不同Re下A,B通道中的时均努塞尔数NuavgTab.2 Time-average Nusselt number in channel A and channel B under different Re

进一步观察发现,在Re≤400的范围内,Nuavg并没有随着Re的增大而绝对增大.具体表现为: B通道中Re在200～400范围内,其Nuavg值大小很是接近,甚至Re=200时的换热Nuavg大于Re= 300,400时的Nuavg;A,B两种通道在Re=100时的换热Nuavg均大于Re=200时的Nuavg.这与通道内的回流区域有关.图6(见下页)为Re=100,200两种工况下,A通道内换热Nu的沿程变化曲线(LX表示距离通道入口的距离);图7(见下页)则表示相应的流线图.经对比发现,通道内回流区的长度随着流动Re的增大而增长,这与Macagno等[11]的实验结果一致.由图7可以看出,两种Re工况下,矩形直肋上游的流场分布特性较相似,在图6中则表现为局部换热Nu大小及变化规律相差无几.在直肋处(流动截面最窄处),借助较强的冲刷能力,通道在Re=200时显现了较强的换热特性;而在直肋下游区域,回流区恶化了流体与壁面间的换热,使得Re=200时的换热强度要弱于Re=100时的换热强度.定量分析结果表明,正是由于上述的“一强一弱”的综合作用,造成了Re=200时通道内的Nuavg反而低于Re=100时的结果.

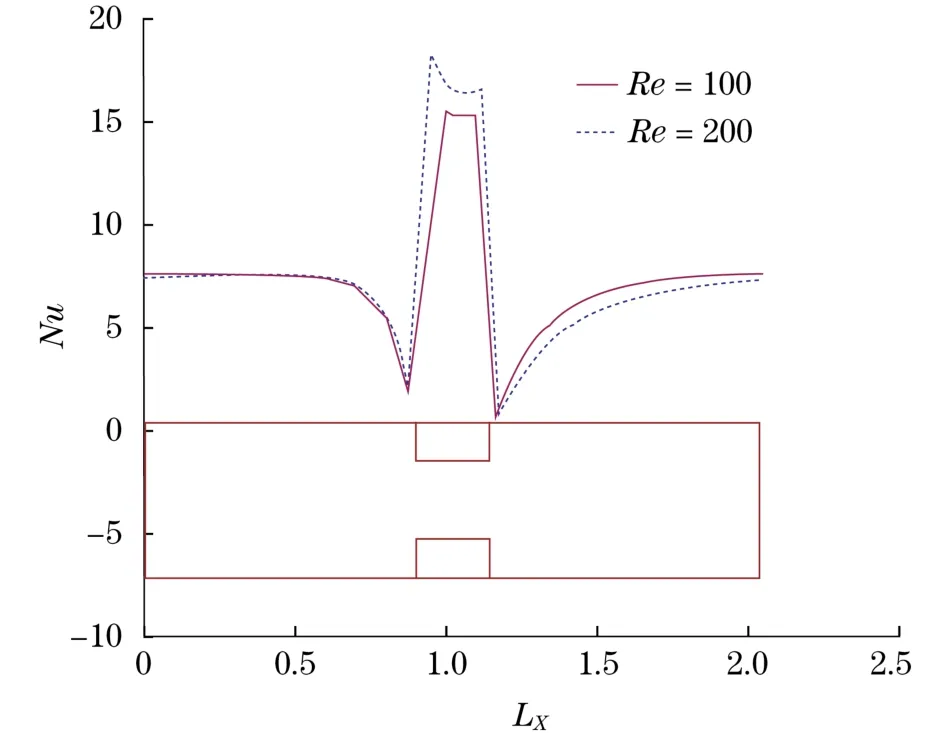
图6 A通道内Nu数的沿程变化Fig.6 Variation of Nusselt values along channel A

图7 A通道流线图Fig.7 Streamline in channel A

3 结 论

在给定条件下得出以下结论:

a.在A,B两种不同直肋形状的周期性通道内均存在丰富的非线性现象.在计算Re范围内,A通道随着Re的增大,系统出现了两种不同的数值解:稳态解和周期性振荡解;而B通道随着Re的增大,系统先后出现了4种不同的数值解,分别为稳态解、周期性振荡解、拟周期振荡解以及混沌解.

b.A通道内系统稳态的临界Re=385,B通道稳态临界Re=440,A通道更早地进入非稳态阶段且振荡幅度也更强烈,但B通道更容易从一种状态过渡到另一种状态.

c.对于一个周期上的时均努塞尔数Nuavg,相同Re时,A通道的Nuavg值大于B通道的.在同一种类型的通道中,Nuavg随Re的增大基本呈增大趋势,但在Re≤400的范围内,Nuavg并没有随着Re的增大而绝对增大.

[1] 张东升,王秋旺,陶文铨.两种渐扩渐缩通道内层流传热特性的比较[J].上海理工大学学报,2001,23(3): 252-254.

[2] Valencia A,Martin J S,Gormaz R.Numerical study of the unsteady flow and heat transfer in channels with periodically mounted square bars[J].Heat and Mass Transfer,2001,37(2/3):265-270.

[3] 汪健生,吴翠.周期性沟槽通道内自激振荡流及换热特性[J].化工学报,2012,63(2):408-415.

[4] 卢玫,董晶瑾,李凌,等.锯齿型通道流动和换热的周期性研究[J].工程热物理学报,2007,28(2):274-276.

[5] 郑建城,杨茉,黄夫泉,等.封闭圆内开缝圆自然对流的非线性特性研究[J].工程热物理学报,2012,33 (2):308-310.

[6] 张晓晖,杨茉,余敏,等.方腔内竖直板振荡的自然对流换热数值研究[J].西安交通大学学报,2004,38 (11):1132-1135.

[7] 仲剑威,卢玫.周期性环肋通道内的流动和换热[J].上海理工大学学报,2009,31(6):535-538.

[8] 董军启,陈江平,袁庆丰,等.板翅换热器平直翅片的传热与阻力性能试验[J].农业机械学报,2007,38 (8):53-56.

[9] Salazar A J,Campo A.Prediction of the thermal entry length without solving the complete entrance length problem[J].Int J Heat Fluid Flow,1990,11(1):48-53.

[10] Adachi T,Uehara H.Correlation between heat transfer and pressure drop in channels with periodically grooved parts[J].Int J of Heat and Mass Transfer, 2001,44(22):4333-4343.

[11] Macagno E O,Hung T K.Computational and experimental study of a captive annular eddy[J].JFluid Mech,1967,28 (1):43-61.

(编辑:石 瑛)

Simulation of Periodically Fully Developed Flow and Heat Transfer in Two Different Channels

LILing1, ZHUSusu1, LIU Jianguo2
(1.School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China; 2.Huaneng Taicang Power Plant,Taicang 215424,China)

Periodic channels with different shapes of straight rib are abstracted from different types of high-efficiency heat exchangers.The heat transfer and fluid flow in the periodic rectangular straight rib channel(A)and the semi-circular straight rib channel(B)were simulated based on the unsteady-state mathematical model under the assumption of periodically fully developed flow.Meanwhile,the heat transfer properties and the demonstrated nonlinear characteristics in two different channels were compared.A low Reynolds number Re,twodimension,laminar forced convection model was adopted when calculated.It is found that when Re is small,the flow and heat transfer present a steady state;when Re is larger than the critical value, unsteady oscillation occurs,and the system shows rich nonlinear phenomena.In the range of calculation,channel A has experienced steady and periodic oscillation phases with the increase of Re;channel B has experienced steady,periodic oscillations,quasi-periodic oscillations and chaos with the increase of Re.

TK 124

A

1007-6735(2015)01-0001-06

10.13255/j.cnki.jusst.2015.01.001

2014-01-04

国家自然科学基金资助项目(51006071)

李 凌(1976-),女,副教授.研究方向:数值传热、强化传热.E-mail:liling@usst.edu.cn