一种适用于嵌入式平台的Raptor码算法
梁 斌
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
一种适用于嵌入式平台的Raptor码算法
梁 斌
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
针对Raptor编/译码器在卫星通信工程应用中运算量过大的不足,提出一种新的稀疏矩阵方程求解算法。采用该算法求解Raptor编/译码方程,可简化求解步骤。与3GPP描述的Raptor码求解算法相比,该算法可有效降低基于嵌入式平台的Raptor编/译码器的运算时间,满足了实际工程中对时延限制和设备小型化的需求。
喷泉码;Raptor码;前向纠错;嵌入式
0 引言
Raptor码[1]是一种新型喷泉码[2],由shokrollahi于2006年提出。与此前Luby提出的喷LT码(Luby Transform)[3]相比,Raptor码具备更好的编译码性能[4]。因此,它被3GPP选定为多媒体组播多播服务(MultimediaBroadcast/Multicast Service,MBMS)中的前向纠错(Forward Error Correc-tion,FEC)算法[5]。在通信设备中常用的嵌入式平台上直接使用3GPP标准中的Raptor编/译码算法,由于其编译码过程的运算量大,且CPU性能有限,导致运算时间延迟过大,无法满足需求。
为解决此问题,本文提出一种新的稀疏矩阵求解算法,对3GPP标准的Raptor编/译码算法中的计算量最大的方程系数矩阵降阶过程进行优化,使其能够满足工程应用。
1 Raptor编译码原理
Raptor码编码和译码过程如图1所示。Raptor编译码运算的基本单位为符号。符号指长度为若干比特的定长数据块。

图1 Raptor码编译码过程
Raptor编码过程可分为预编码和LT编码。在预编码过程中,输入的数据块被分割为1~k个符号,并通过编码矩阵运算转化为中间符号。LT编码过程则根据中间符号和编码符号ID(Encoded Symbol ID,ESI)产生1~m个编码符号。因喷泉码为无率码,m理论上可取无穷大的整数。在实际应用中,则根据信道状况确定m的取值。
编码符号序列通过删除信道后进入Raptor译码器。Raptor译码过程同样可分为预译码和LT译码。预译码过程将收到的编码符号序列恢复成中间符号。因Raptor码为系统码,前k个编码符号与原始数据相同。LT译码过程只需根据中间符号生成1~k个编码符号,即可恢复原始数据。
Raptor预编/译码过程可等价为模2线性方程组求解。其编/译码线性方程组的系数矩阵即为Raptor编/译码矩阵。3GPP推荐的Raptor编码矩阵由LDPC[6,7]矩阵、Half矩阵、单位阵和前k个符号对应的伪随机数向量组成,其整体为一个方阵;译码矩阵则由LDPC[7,8]矩阵、Half矩阵、单位阵和n个伪随机向量组成,其整体为一个长方形矩阵。其中n为1~m个编码符号通过删除信道后,被译码器接收到的符号个数。Raptor预编/译码过程就是将编/译码矩阵转换为单位阵的过程。此操作完成后,中间符号就会被求取出来。然后,LT编码过程则根据中间符号和ESI信息,通过一系列运算和查表操作,生成该ESI对应的编码符号。
由线性代数相关知识可知,线程方程组有解的充要条件是其系数矩阵满秩。Raptor编码矩阵的产生规则可保证其必然为满秩方阵。但是Raptor译码矩阵与接收符号对应的向量相关,因而导致其不一定满秩。如译码矩阵不满秩,则Raptor译码失败。因此,Raptor译码存在失败概率。人们经过长期试验,总结出Raptor码译码失败概率为:

式中,n为译码器收到的编码符号数量;k为编码原始数据包含的符号数量。当n<k的时候,译码矩阵的行数低于列数,必然不满秩,译码失败概率为1。当n≥k的时候,译码系数矩阵行数大于等于列数,矩阵有可能满秩。随着(n-k)的增加,Raptor码的译码失败概率会降低。当(n-k)=30时,译码失败概率为10-9量级。因此,要保证译码成功率,必须确保一定的接收符号冗余量。
由此不难发现,k越大,冗余量在接收符号中所占的比例(n-k)/n就越小,Raptor码的传输效率就越高。单从这个角度看,Raptor码的k取值越大越好。但随着k的增加,编/译码矩阵也就变得越来越大,进而导致预编/译码的方程求解过程变的更加复杂。导致运算时间增加,编译码时间延迟增大,数据吞吐量降低。与之相比LT编码过程的计算量几乎可以忽略不计。因此,优化Raptor编译码过程的重点是优化预编/译码过程,而优化预/编译码过程的本质则是优化模2线性方程组的求解过程,使用尽量少的步骤求解出Raptor编/译码方程。
2 3GPP描述的矩阵求解算法
求解线性方程组的基本方法是高斯消元法。但是直接使用高斯消元法求解方程组的复杂度非常高,约为k的3次方量级。且整个过程为串行处理过程,难以使用并行处理的方法提高效率。
为了解决编译码性能和计算复杂度的矛盾,3GPP提出了一种较为高效的求解方法。它利用Raptor编/译码矩阵为稀疏矩阵,先将其降阶,然后再进行高斯消去,进而达到降低运算复杂度的目的。该处理过程如下[9]:令方程系数矩阵为A。定义行重为矩阵A某一行包含的1的个数。r为矩阵A中的非零最小行重值。如图2(a)所示,令矩阵V=A。令矩阵U为空矩阵。按照如下步骤运算,逐渐将矩阵V转换成图2(b)所示的分块矩阵状况。

图2 3GPP算法求解示意
步骤1:在矩阵V中查找r最小的行。如果r≠2,则任选一行;如果r=2,任选包含在矩阵V诱导的二分图G中的最大尺度环的1行。
步骤2:将前一部中所选的行与V中的第1行进行交换,且V中的列进行重排,重排后的非零元素除了第1个放置在首列以外,其他非零元素全部放置在V的后部。
步骤3:V中的首列非零的行与首行执行行加减操作,以使得V中除了第1行外的首列全部变成0。
步骤4:V的各行尾部元素移入矩阵U。跳回到步骤1。
此算法反复执行后,使矩阵V逐渐变小直至消失,变为图2(c)所示状况。将矩阵U的元素可划分为矩阵UU和矩阵Ul,如图2(d)所示,。Ul即为降阶产生的稠密矩阵。使用高斯消去求解出Ul,然后用该结果求解出UU。最终求解中所有的结果。
本算法在X86平台运行的效果尚可,但移植到嵌入式平台后,因嵌入式CPU的处理能力有限,导致其数据吞吐量大幅降低,编译码时间显著增加。要开发出具有实用价值的Raptor编/译码,必须对该算法进行优化改进。
3 基于分组法降阶的矩阵求解算法
线性方程组总是存在一个最优求解步骤,依照该步骤对各行进行消元操作,可以用最少的步骤求解出方程。在每一步运算中,需执行2个操作:决策和消元。3GPP算法在嵌入式平台上之所以效率明显降低,是因为其决策过程过于复杂。例如矩阵V诱导的二分图G中的最大尺度环的求取过程,涉及了大量查找和排序操作。要降低决策时间,必须设法在不进行查找及排序的情况下完成决策过程。
分组求解法正是基于此思路设计,以分组代替排序和查找。先求解出一些易于求解的变量,当求解决策代价增加到一定程度后,就放弃决策,改用高斯消元处理剩余方程。其基本步骤如下:
步骤1 如图3(a)所示,以r为依据对矩阵各行分组r=1组中的行每行只包含一个非零系数。r=2组中的行包含2个非零系数。其余各行分为2组,即设定一个界限值Min,r小于等于该界限值的行组成r≤Min组。r大于该界限值的行组成r>Min组。设置2个空组为最终组和接近最终组。
步骤2 如图3(b)所示,指定r=1组中的一行为操作行。用该行对其他各行进行行加减操作。如被处理行的r变化,则将其归入对应组。操作行归入最终组。直到r=1组中无元素。
步骤3 如图3(c)所示,指定r=2组中的一行为操作行。用该行对其他各行进行行加减操作。如被处理行的r变化,则将其归入对应组。操作行归入接近最终组。如出现r=1的行,则执行步骤2。直到r=2组中无元素。
步骤4 如图3(d)所示,指定r≤Min组中的一行为操作行。用该行对其他各行进行行加减操作。如被处理行的r变化,则将其归入对应组。操作行归入接近最终组。如出现r=1的行,则执行步骤2。如出现r=2的行,则执行步骤3。直到r≤Min组中无元素。
步骤5 如图3(e)所示,用高斯消元法求解r>Min组中的方程。
步骤6 如图3(f)所示,用步骤5的结果求解接近最终组,进而求解出全部结果。
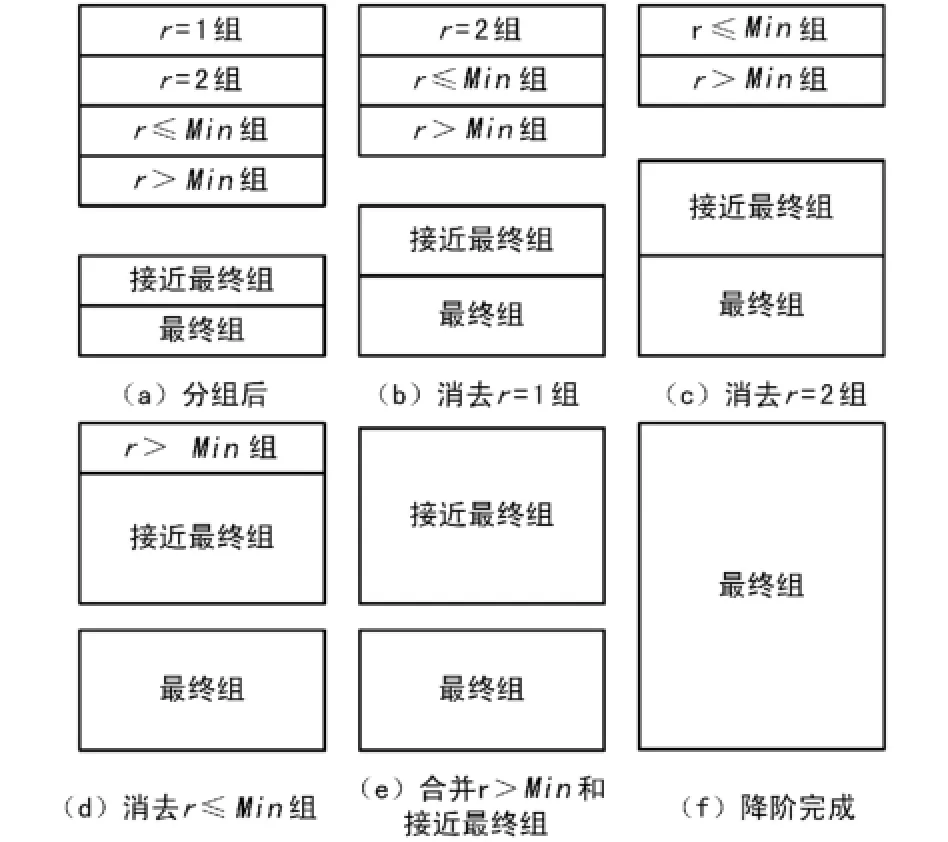
图3 分组法求解示意
4 2种求解算法的比较
因节省了查找和排序时间,分组法的矩阵降阶速度比3GPP算法快。但是分组法的产生的稠密矩阵比3GPP大。通过控制k和调整Min的取值,分组求解算法可保证其在嵌入式平台上的处理时间满足吞吐量指标和时间延迟的要求。
分组求解算法的决策代价较低,可用行加减次数来衡量算法的运算复杂度。以k=200为例,使用高斯消元法,需要执行约16 000次行加减操作,而使用分组法只需要执行5 125次行加减操作。分组法求解法较高斯消元法的计算效率明显提高。
与3GPP算法相比,由于分组求解法的决策过程简单,使得其在实际运算中的整体耗时有所降低。在计算机模拟测试中,k值取512及以下参数中,分组法的数据处理能力普遍高于3GPP算法,而在嵌入式平台上,分组求解法的优势更加明显。
分组求解法在S3C6410上运行的结果打印如图4所示。S3C6410是三星公司生产的一款基于ARM11体系结构的精简指令集处理器[10],其运算能力并不突出。采用分组法算法,k取320,编码符号长度为31 bytes,编码420个符号的情况下,S3C6410芯片可在60 ms左右时间完成Raptor码编码操作。该速度较基于3GPP算法的程序约提高了2倍左右。

图4 S3C6410计算k=320矩阵的结果
5 结束语
本文介绍的适用于嵌入式平台的Raptor码算法,有效降低了Raptor编译码算法中矩阵降阶的运算复杂度,进而降低了总运算时间,使得在嵌入式CPU上,能够实现较高速度,较低时延的Raptor编/译码运算逻辑。这使得Raptor码编译码器的硬件体积显著降低,能够方便地集成在设备中。该算法为Raptor编/译码技术的应用与推广提供了一种可行的解决方案。
[1]SHOKROLLAHI A.Raptor Codes[R].Digital Fountain,Technical Report,2003:1-37.
[2]LUBY M,MITZENMACHER M,SHOKROLLAHI A.Prac-tical Loss-resilient Codes[C]∥Proceedings of the 43rd Annual IEEE Symposium on the Foundations of Computer Science,1997:150-159.
[3]LUBY M.LT-codes[C]∥Proceedings of the 43rd Annual IEEESymposiumontheFoundationsofComputer Science,2002:271-280.
[4]LUBY M,MITZENMACHER M,SHOKROLLAHI A,et al.Efficient Erasure Correcting Codes[J].IEEE Transa-ction on Information Theory,2001,47(2):569-584.
[5]3GPP TS 26.346 V7.0.0.Technical Specification Group Services and System Aspects:Multimedia Broadcast/Mul-ticast Service:Protocols and Codes[S],2007.
[6]吴 琼,梅进杰.改进Min sum的LDPC译码算法研究[J].无线电通信技术,2012,38(2):27-29.
[7]陈远友.一种用于短猝发通信的LDPC短码设计[J].无线电通信技术,2014,40(1):32-33.
[8]赵建功,刘香玲.准循环LDPC码的部分并行译码算法[J].无线电工程,2012,42(2):55-57.
[9]3GPP TS 26.346 version 6.3.0.FEC encoder specification[S],2005.
[10]孙连文,朱正礼,马艳婷.基于S3C6410处理器的嵌入式Linux系统的构建[J].计算机与现代化,2013(11):155-157.
A Raptor Code Algorithm for Embedded Platform
LIANG Bin
(The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China)
To solve the problem that the calculations of Raptor encoder/decoder is too complex to apply in satellite communication project,a novel sparse matrix rank reduction method is proposed.The method used to solve Raptor encoding/decoding equation can sim-plify the process of solution.Compared with the algorithm recommended by 3GPP,the method can effectively reduce the running time of Raptor encoder/decoder based on embedded platform,and can meet the requirements of time delay and equipment miniaturization in practical engineering.
fountain codes;Raptor code;FEC;embedded
TP391.4
A
1003-3106(2015)10-0077-04
10.3969/j.issn.1003-3106.2015.10.21
梁 斌.一种适用于嵌入式平台的Raptor码算法[J].无线电工程,2015,45(10):77-80.
梁 斌男,(1982—),硕士,工程师。主要研究方向:卫星通信与广播电视。
2015-07-28

