梯度拉伸下锯齿型石墨烯褶皱的分子动力学模拟*

黄健彰 韩强

(华南理工大学土木与交通学院，广东广州510640)

梯度拉伸下锯齿型石墨烯褶皱的分子动力学模拟*

黄健彰 韩强†

(华南理工大学土木与交通学院，广东广州510640)

针对梯度拉伸荷载作用下正方形锯齿型石墨烯薄膜的褶皱变形进行了分子动力学模拟.研究了石墨烯表面形成褶皱的发展、演化过程，揭示了边界条件和荷载条件对石墨烯褶皱变形的重要影响，得到了褶皱波幅、波长、离面位移和褶皱方向角等随加载位移的变化规律，研究了石墨烯尺寸、温度和荷载梯度对石墨烯褶皱变形的影响.结果表明:褶皱的发展、演化过程可分为褶皱前期、中期、后期、末期4个阶段;随着加载位移增加，褶皱幅值、幅值波长比和最大离面位移逐渐增大，褶皱波长和方向角则减小;尺寸和温度对石墨烯褶皱都会产生重要影响，而荷载梯度对石墨烯褶皱影响甚微.

石墨烯;分子动力学;褶皱;梯度拉伸荷载;边界条件

石墨烯具有极为优越的力学、热学和电学性能，已成为纳米力学领域的研究热点之一［1-2］，其优异的物理学特性使它成为了重要的纳米元件［3］.石墨烯单层原子厚度和其极小的弯曲刚度导致它很容易形成褶皱.2007年Meyer等［4］首先发现石墨烯表面形成了褶皱.石墨烯的褶皱可以由不同的外界激励引起，例如官能团的影响、结构的缺陷、热涨落和机械扰动等［5］.褶皱对石墨烯的力学性能、电子学性能、热学和化学性能等具有重要影响.Zhu等［6］的研究指出褶皱会影响石墨烯的电子运输性能，能降低纳米器件的开闭比和提高整个器件的电阻.Chen等［7］通过微拉曼映射技术证明了褶皱会降低石墨烯的导热系数.Zheng等［8］的研究指出石墨烯能取代铟锡氧化物成为新型的透明导电膜，而且具有高密度褶皱的石墨烯是用于制造储氢器件、超级电容器和纳米机械元件的最佳选择.褶皱使石墨烯表面具有极高的粘附力，使得石墨烯和聚合物基体有紧密的机械锲合，从而提高石墨烯增强复合材料的力学性能［9-10］.Levy等［11］的研究表明，石墨烯上的褶皱能导致一个高达300T以上的伪磁场.同时，可以通过调控石墨烯褶皱构形、方向、波长和波幅以满足工程应用的不同需要.因此，研究石墨烯褶皱形成的物理本质，揭示石墨烯褶皱的发展演化过程具有重要的学术和工程价值.

目前，对于石墨烯褶皱的研究多集中于褶皱对石墨烯的物理性能产生的影响，鲜见对石墨烯褶皱物理本质进行解释.石墨烯褶皱的物理本质尚未清晰，石墨烯褶皱的理论尚未建立.现有的研究中，主要集中于获得石墨烯的褶皱图案、波长和波幅.在这些研究中，产生石墨烯褶皱变形的模拟多为对不同几何形状的石墨烯进行简单的拉伸、压缩和剪切，边界条件多为固定边界［12-17］，尚未有涉及梯度荷载和复杂边界条件的石墨烯褶皱变形的研究.文中基于分子动力学方法，以锯齿型正方形石墨烯为研究对象，通过对石墨烯施加边界条件和荷载条件，分析了在梯度拉伸荷载作用下石墨烯的褶皱变形机理.通过研究石墨烯的褶皱构形、褶皱参数和参考点的离面位移变化历程等，分析了石墨烯的褶皱变形的形成、发展和演化过程，得到了褶皱参数的变化规律.最后研究了石墨烯尺寸、温度和荷载梯度对石墨烯的褶皱变形的影响.

1 石墨烯薄膜的分子动力学模型

正方形单层锯齿型石墨烯尺寸为6.2392nm×6.0173nm，其碳原子质量为12个原子质量单位，C—C键长为0.142nm.边界条件和加载条件如图1所示.在石墨烯上设置截断线I，x=1.560 nm，参考点A(0.5672nm，0.0614nm).

图1 石墨烯边界、荷载与截断线IFig.1 Boundary and load condition of graphene aswell as line I

针对在梯度拉伸载荷下单层正方形石墨烯的褶皱变形进行分子动力学模拟，采用AIREBO势函数，模拟在NVT系综下进行，采用Nose-Hoover热浴法进行温度调节，温度为0.01K，时间步长为1 fs，采用LAMMPS默认的Velocity-Verlet积分算法.加载前，对石墨烯进行充分的无约束弛豫，系统完成能量最低化后，以位移形式加载，位移d从0到0.01nm线性变化.每加载一次后进行10 ps的分子动力学弛豫，共加载 250次，C—C键的截断半径设定为0.2nm.

2 石墨烯褶皱的变形及构形参数

石墨烯的褶皱是石墨烯在外载荷作用下产生的.褶皱具有特定的方向性和自相似性.当移除外载荷后这些波纹会消失，因此褶皱具有可逆性.为了描述石墨烯褶皱的特征，定义n为褶皱数量即褶皱波峰和波谷的总数，如褶皱数量n记为3(1，2)表示褶皱数量为3，其中波峰数为1，波谷数为2.褶皱波长、波幅、方向角等褶皱参数如图2所示.

为表示石墨烯整体褶皱的特征，定义参数为

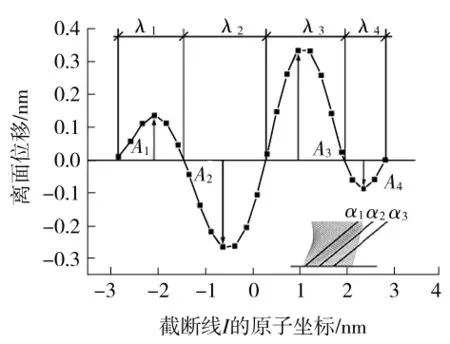
图2 dmax=1.5nm时截断线I的褶皱形状Fig.2 Wrinkling shape of line I when dmax=1.5nm

式中，η表示特定的褶皱参数，如褶皱幅值ηA，褶皱波长ηλ，褶皱方向角ηα和褶皱幅值波长比ηA/ηλ.褶皱方向角ηα为褶皱的方向与水平方向上的夹角，如图2所示.褶皱的幅值波长比ηA/ηλ能够反映褶皱的形态，幅值波长比越大，说明褶皱越高耸;反之亦然.褶皱参皱η-反映石墨烯的整体褶皱特征.

图3所示是dmax为0.5、1.0、1.5、2.0nm时的褶皱构形.石墨烯表面形成了非均匀的褶皱群.褶皱的规模从右下角到左上角逐渐增大.随着dmax的增大，在石墨烯右下角处的褶皱开始密集.左边界为自由边界，因此石墨烯左上方产生较大的离面变形.造成以上现象的原因与石墨烯的几何形状、荷载和约束条件有一定的关系.固定边界限制了其碳原子的面内自由度，从而引入压应力.固定边界引入的压应力与梯度荷载的共同作用造成石墨烯形成一系列梯度变化的褶皱.

开始加载时，石墨烯结构处于弹性阶段.dmax增加到0.5nm时，石墨烯表面出现褶皱，如图3(a)所示，褶皱倾斜而具有一定的方向角，褶皱数量为2(1，1).当dmax=1.0 nm时，在石墨烯的右上角和右下角出现较小的新褶皱，褶皱数量增加到4(2，2).当dmax=1.5nm时，褶皱方向角明显减少，褶皱显得更倾斜.当dmax=2.0nm时，简支边界已经明显变形，简支边界上的碳原子有向石墨烯中央靠拢的趋势.石墨烯右上角的C—C键已被高度拉伸濒临断裂破坏，褶皱群变得紧凑、细长，褶皱面积大.

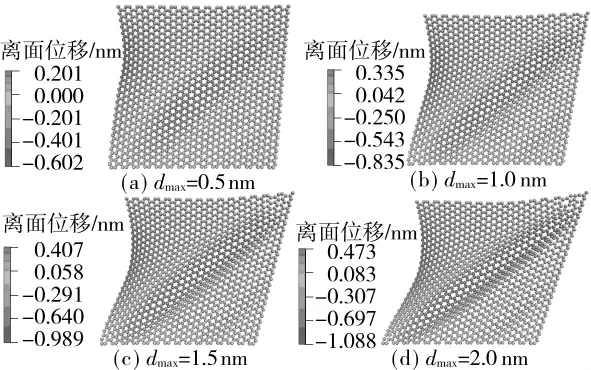
图3 石墨烯的褶皱构形Fig.3 Wrinkling configurations of graphene

图4为参考点A的离面位移变化曲线.石墨烯褶皱的变形发展过程可分为4个阶段:(Ⅰ)褶皱前期阶段;(Ⅱ)褶皱中期阶段;(Ⅲ)褶皱后期阶段; (Ⅳ)褶皱末期阶段.开始加载后一段时间内，由于弛豫过程，石墨烯表面上产生的波纹为主要特征.石墨烯表面的碳原子在离面方向振动，但未形成褶皱.这个阶段为褶皱前期阶段，以dmax=0.157 nm为终点.当0.157nm＜dmax≤0.584nm时，为褶皱中期阶段.此阶段内，褶皱已形成并以较快速度发展.褶皱发展过程中，参考点都有不同程度的颤动.褶皱发展不稳定，随着加载进行，褶皱上的原子在离面方向上往复运动.当0.584nm＜dmax≤1.305nm时，为褶皱后期阶段.这是褶皱的稳定发展阶段，石墨烯上的碳原子没有颤动，褶皱发展速度下降.当dmax到达1.305nm后，褶皱发展进入末期阶段.褶皱最终构形基本成型，随后石墨烯濒临破坏，褶皱出现不稳定的波动现象.此阶段持续至石墨烯失效破坏(dmax=2.281nm)，体现在参考点的离面位移剧烈变化上.

图4 石墨烯参考点的离面位移Fig.4 Out-of-plane displacement of key point of graphene

截断线I上的褶皱参数结果如表1所示，褶皱波幅和幅值波长比都随着载荷的增加而增大，而波长是呈减少的趋势.反映出随着载荷加载，石墨烯上有高度褶皱的趋势.同时，褶皱从2个增加到4个后，石墨烯褶皱数量不再增加，只是褶皱幅值和波长发生变化.文中假设褶皱是相互平行的，即方向角相同.表1列出了褶皱方向角ηα和最大离面位移wE.ηα随着荷载的加载而越来越小，褶皱越向加载方向倾斜;wE随着荷载的加载持续增大，直到石墨烯破坏前，wE值为1.088nm.图5所示为褶皱参数随dmax变化的曲线.曲线上有一突变处，因为次级褶皱即新的小型褶皱的产生影响了参数的平均值.总体看来，褶皱幅值和幅值波长比都是呈增长趋势;褶皱波长在新褶皱出现后剧减，后来则缓慢减少.

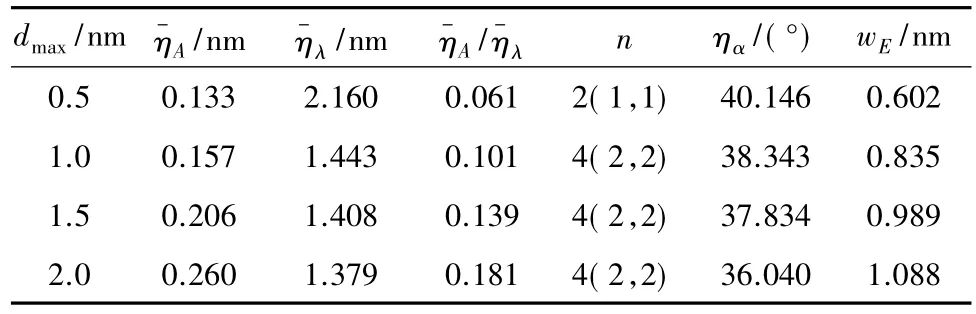
表1 不同加载位移下的褶皱参数结果Table 1 Wrinkling parameters at different dmaxvalues

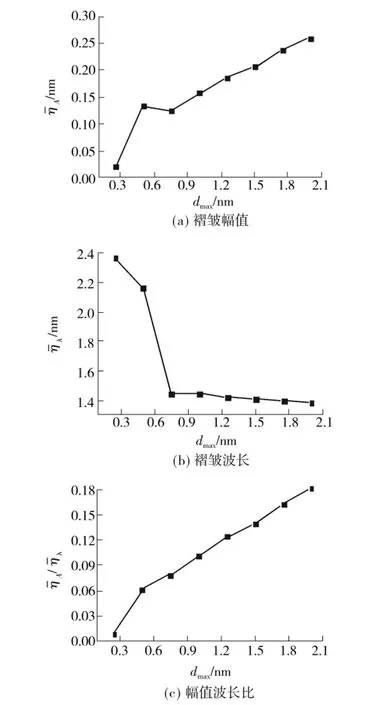
图5 褶皱参数随dmax变化的曲线Fig.5 Wrinkling parameter curves varying with dmax

3 尺寸、温度与荷载梯度对石墨烯的褶皱变形的影响

3.1 荷载梯度的影响

选取边长为6nm的石墨烯模型，设置每次加载时，荷载梯度 kd分别为1.000×10-3、1.333×10-3、1.667×10-3、2.000×10-3、2.333×10-3、2.667×10-3，控制其他条件不变，研究在相同dmax=1.0nm下的褶皱构形和参数的差别.具体的褶皱构形和褶皱参数的结果见图6和表2.从表2的结果可以看出，荷载梯度对褶皱幅值、褶皱波长和褶皱方向角褶皱参数的影响甚微，但对wE产生影响，随着荷载梯度的增加，先减少后增加.不同荷载梯度下的褶皱构形差异很小.说明在梯度剪切荷载作用下，荷载梯度对石墨烯褶皱行为影响较小.

图6 不同荷载梯度下的褶皱构形(dmax=1.0nm)Fig.6 Wrinkling configurations at different loading grads(dmax= 1.0nm)

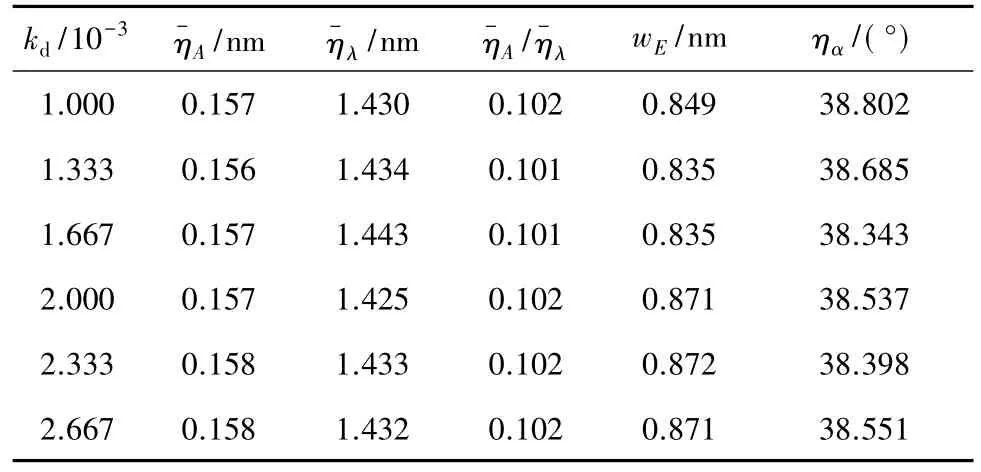
表2 不同荷载梯度下的褶皱参数(dmax=1.0nm)Table 2 Wrinkling parameters at different loading grads(dmax= 1.0nm)

3.2 温度的影响

选取以边长为6nm的石墨烯模型，分别设置温度为0.01、100、200、300、400、500K，控制其他条件不变，研究了在相同dmax(dmax=1.0 nm)下的褶皱构形和参数的差别.

褶皱参数和褶皱构形见表3和图7.根据表3，褶皱参数随着温度增加呈现不规律变化，特别是300K温度下的褶皱参数与其他温度下的参数有明显差异，说明温度对褶皱参数的影响非常大.不同温度下，尽管褶皱数量都是4(2，2)，但石墨烯的褶皱构形明显不同.温度的存在使碳原子的热振动加剧，因此对石墨烯的褶皱行为产生不可忽略的影响.除0.01K温度外的石墨烯褶皱构形都是石墨烯热效应行为和梯度拉伸荷载的共同作用产生的结果，说明温度对石墨烯褶皱行为产生了重要影响.

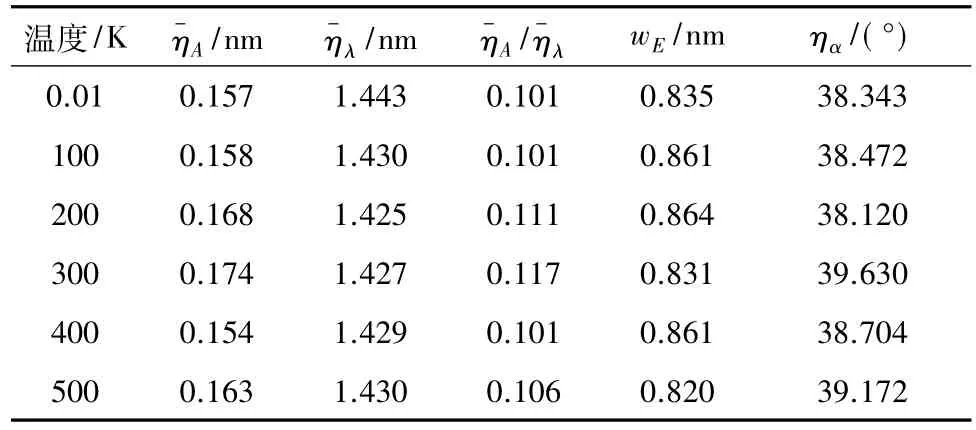
表3 不同温度下的褶皱参数(dmax=1.0nm)Table 3 Wrinkling parameters at different temperatures(dmax= 1.0nm)

图7 不同温度下的褶皱构形(dmax=1.0nm)Fig.7 Wrinkling configurations at different temperatures(dmax= 1.0nm)

3.3 尺寸的影响

选取边长为4、6、8、10nm的石墨烯作为模型，控制其他条件不变，研究了加载边界斜率k=0.192下的褶皱构形和参数的差异.对长度性质的参量进行归一化处理，例如η-/b，其中b为正方形石墨烯边长.

褶皱参数和构形见表4和图8.根据表4，总的来说，随着尺寸的增大，wE、褶皱幅值波长比和褶皱波幅都呈增长趋势;褶皱波长随着尺寸的增加而减小;褶皱方向角随着尺寸增加先减小后增大;褶皱数量增加到4(2，2)后即不再增加.这说明尺寸的增大使得石墨烯褶皱形态更细长、更高耸.如图8所示，尺寸越大褶皱数量越多，褶皱构形也发生变化.随着尺寸的增加，在靠近自由边界区域处新增一个与原靠近此区域的褶皱类型相反的褶皱，即是，若原靠近自由边界区域的褶皱为一个波峰，随着尺寸的增加，在自由边界附近区域会产生一个波谷，从而增加褶皱数量，反之亦然.也可认为，小尺寸石墨烯的褶皱构形是从大尺寸石墨烯褶皱中分离出来的.

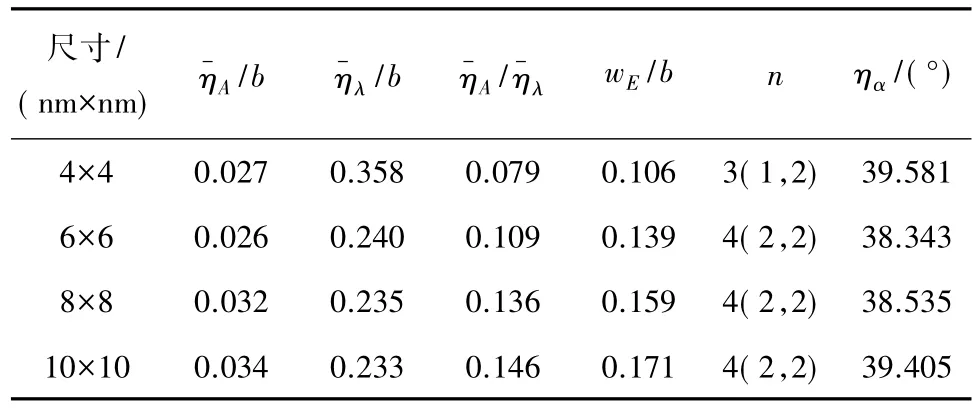
表4 不同尺寸下的褶皱参数(k=0.192)Table 4 Wrinkling parameters in different sizes(k=0.192)

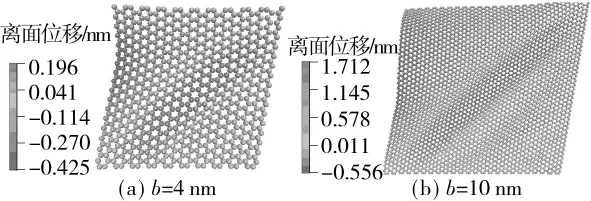
图8 不同尺寸下的褶皱构形(k=0.192)Fig.8 Wrinkling configurations in different sizes(k=0.192)

4 结论

文中运用分子动力学方法研究了包含自由边界、简支边界和固支边界的复杂边界条件的正方形锯齿型石墨烯在梯度拉伸荷载下的褶皱变形.结果表明，在石墨烯表面上形成了梯度变化的褶皱群，褶皱随着载荷位移的增大而变得密集紧凑、细长，简支边界上碳原子向石墨烯中央靠拢.上述结果与石墨烯的几何构形、约束和载荷有关.褶皱的发展、演化过程可分为4个阶段，分别为褶皱前期、中期、后期和末期阶段.总的来说，褶皱幅值、幅值波长比和最大离面位移随加载位移增加而增加;褶皱波长和方向角则随加载位移增加而减少.另外，石墨烯尺寸和温度对锯齿型石墨烯褶皱都产生很大的影响.文中还提出了褶皱随尺寸增加而增加的规律;发现了温度对褶皱的发展、演化过程产生重要影响，非零温度下石墨烯的褶皱变形是温度效应行为与梯度拉伸荷载共同作用的结果;荷载梯度对锯齿型石墨烯褶皱没有明显的影响.

［1］ 韩强，黄凌燕.石墨烯薄膜拉伸性能的分子动力学模拟［J］.华南理工大学学报:自然科学版，2012，40(2): 29-34.

Han Qiang，Huang Ling-yan.Molecular dynamics simulation of tensile properties of graphene sheets［J］.Journal of South China University of Technology:Natural Science E-dition，2012，40(2):29-34.

［2］ 黄凌燕，韩强.单层石墨烯温度效应的分子动力学模拟［J］.中国科学:物理学力学天文学，2012，42(3):319-326.

Huang Ling-yan，Han Qiang.Molecular dynamics simulation of temperature effect on mono-layer graphene sheets［J］.Scientia Sinica Physica，Mechanica＆Astronomica，2012，42(3):319-326.

［3］ Schedin F，Geim A K，Morozov SV，et al.Detection of individual gasmolecules adsorbed on graphene［J］.Nature Materials，2007，6(9):652-655.

［4］ Meyer JC，Geim A K，Katsnelson M I，et al.The structure of suspended graphene sheets［J］.Nature，2007，446 (7131):60-63.

［5］ Zheng Q，Geng Y，Wang S，et al.Effects of functional groups on the mechanical and wrinkling properties of graphene sheets［J］.Carbon，2010，48(15):4315-4322.

［6］ Zhu W，Low T，Perebeinos V，etal.Structure and electronic transport in graphene wrinkles［J］.Nano Letters，2012，12(7):3431-3436.

［7］ Chen S，Li Q，Zhang Q，et al.Thermal conductivity measurements of suspended graphene with and without wrinkles by micro-Raman mapping［J］.Nanotechnology，2012，23(36):365701.

［8］ Zheng Q，Ip W H，Lin X，et al.Transparent conductive films consisting of ultralarge graphene sheets produced by Langmuir-Blodgett assembly［J］.ACS Nano，2011，5 (7):6039-6051.

［9］ Koenig SP，Boddeti N G，Dunn M L，et al.Ultrastrong adhesion of graphene membranes［J］.Nat Nano，2011，6 (9):543-546.

［10］ Rafiee M A，Rafiee J，Wang Z，et al.Enhanced mechanical properties of nanocomposites at low graphene content［J］.ACSNano，2009，3(12):3884-3890.

［11］ Levy N，Burke S A，Meaker K L，et al.Strain-induced pseudo-magnetic fields greater than 300 Tesla in graphene nanobubbles［J］.Science，2010，329(5991): 544-547.

［12］ Wang C，Mylvaganam K，Zhang L.Wrinkling ofmonolayer graphene:a study by molecular dynamics and continuum plate theory［J］.Physical Review B，2009，80(15): 155455.

［13］ Gil A J，Adhikari S，Scarpa F，et al.The formation of wrinkles in single-layer graphene sheets under nanoindentation［J］.Journal of Physics Condensed Matter:an Institute of Physics Journal，2010，22(14):145302.

［14］ Zhang Z，Duan W H，Wang C M.Tunable wrinkling pattern in annular graphene under circular shearing at inner edge［J］.Nanoscale，2012，4(16):5077-5081.

［15］ Duan W H，Gong K，Wang Q.Controlling the formation of wrinkles in a single layer graphene sheet subjected to inplane shear［J］.Carbon，2011，49(9):3107-3112.

［16］ Min K，Aluru N R.Mechanical properties of graphene under shear deformation［J］.Applied Physics Letters，2011，98(1):013113.

［17］ Wang C，Liu Y，Lan L，et al.Graphene wrinkling:formation，evolution and collapse［J］.Nanoscale，2013，5 (10):4454-4461.

M olecular Dynam ics Simulation of W rink les in Zigzag Graphene Under Gradient Tension

Huang Jian-zhang Han Qiang
(School of Civil Engineering and Transportation，South China University of Technology，Guangzhou 510640，Guangdong，China)

This paper dealswithmolecular dynamics simulation of the wrinkling deformation of a zigzag square single-layer graphene sheet(SLGS)subjected to gradient tensions.In the investigation，the formation and evolution of the wrinkles on graphene surface are analyzed，and the effects of boundary and loading conditions on thewrinkling deformation are explored.Then，the variations of the wrinkling amplitude，the wavelength，the out-of-plane displacement and the direction angle with the loading displacement are revealed，and the effects of graphene size，temperature and loading grad on the wrinkling are discussed.It is found that(1)the formation and evolution process ofwrinkles can be divided into four stages，namely the prophase stage，the metaphase stage，the anaphase stage and the telophase stage;(2)with the increase in loading displacement，thewrinkling amplitude，the ratio of amplitude to wavelength and the maximum out-of-plane displacement all increase，while the wrinkling wavelength and the direction angle decrease;and(3)both the size and the temperature remarkably affect the graphene wrinkling，while the loading grad has little effect on the wrinkling.

graphene;molecular dynamics;wrinkle;gradient tension load;boundary condition

s:Supported by the National Natural Science Foundation of China(11272123，11472108)

TB39

10.3969/j.issn.1000-565X.2015.06.019

1000-565X(2015)06-0122-05

2014-09-29

国家自然科学基金资助项目(11272123，11472108)

黄健彰(1992-)，男，博士生，主要从事纳米力学研究.E-mail:h.jianzhang@mail.scut.edu.cn

†通信作者:韩强(1963-)，男，教授，博士生导师，主要从事非线性动力学研究.E-mail:emqhan@scut.edu.cn