一类带吸附项双重退化奇异扩散方程的解
欧阳苗
(厦门理工学院应用数学学院,福建厦门361024)
一类带吸附项双重退化奇异扩散方程的解
欧阳苗
(厦门理工学院应用数学学院,福建厦门361024)
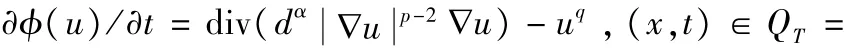
双重退化;扩散方程;存在性;唯一性
关于一般的双重退化奇异扩散方程
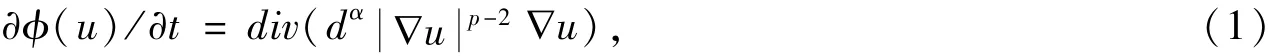
文献 [1]详细给出了解的存在唯一性.当α=0,方程 (1)为发展P-Laplace方程

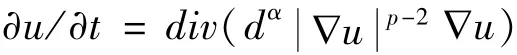

式(3)中:Ω是RN中边界∂Ω充分光滑的有界区域;d(x)=dist(x,∂Ω);p>1;q>1;α>0;φ∈C2,且存在δ>0使得φ′(s)>δ>0.
1 弱解的定义及主要结论
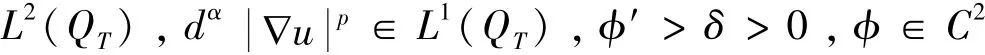

根据文献 [2],方程 (3)在边界上退化,即使在有界区域上,边值问题依赖于热扩散系数消失比率α的大小.若0<α<p-1,给齐次Dirichlet边值条件:
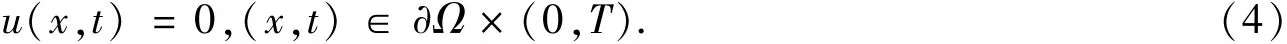
若α≥p-1,方程 (3)的热传导问题不受边界条件的限制.初值条件总是必需的:

对于方程 (1),文献 [1]得到了命题1和命题2.

命题2设α≥p-1,无需边值条件,方程 (1)(5)最多只有一个解.
本文证明带吸附项的双重退化奇异扩散方程 (3)有以下结论:

定理2设α≥p-1,无需边值条件,方程 (3)(5)最多只有一个解.
2 证明
为研究方程 (3),考虑它的正则化问题:
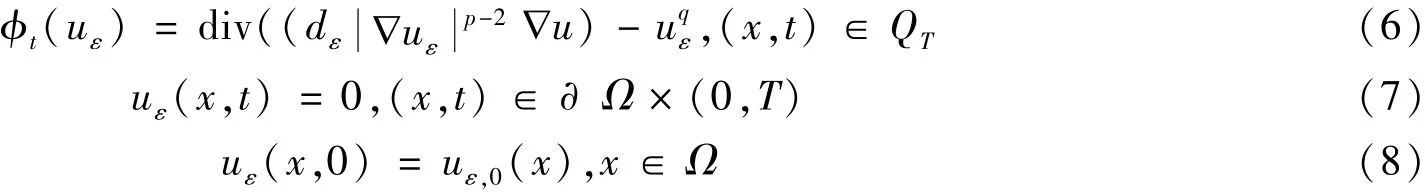
其中dε=d+ε,ε>0.解的性质与发展P-Laplace方程类似,即:
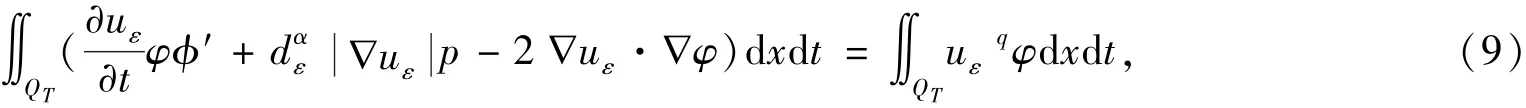
且 (8)在迹的意义下成立.



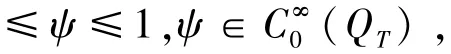
故引理得证.
2.1 定理1的证明
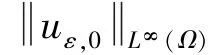
由于α/(p-1)<1,p-α>1,存在常数β∈(α/(p-1),1)使得p-α/β>1.由β<1,p-α/β>1,不难得知存在常数γ∈(1,p-α/β)使得βγ<1.故
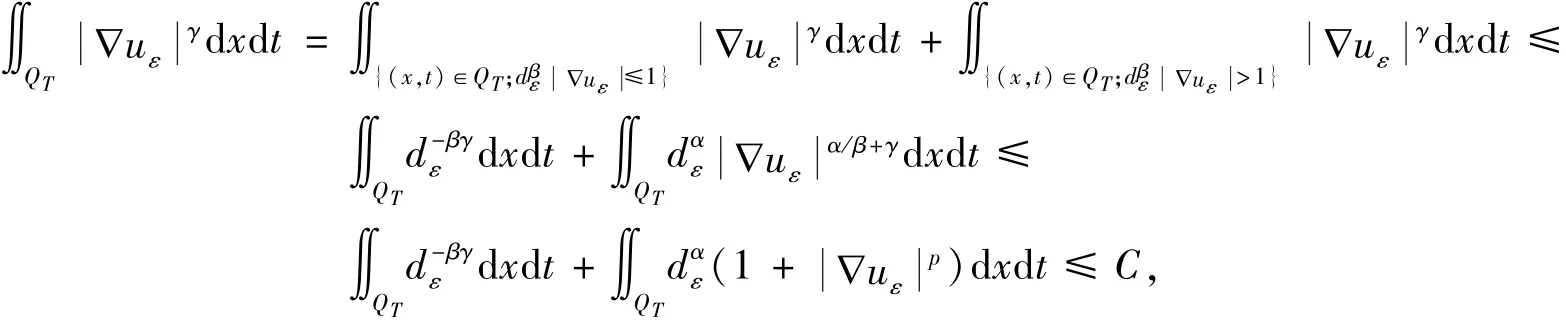
C是与ε无关的正常数.即∇uε在Lγ(QT)中一致有界,得证u满足边界条件 (4).
唯一性:设u和v均是初边值问题 (3)(4)(5)的弱解,u(x,0)=v(x,0).由弱解定义,任何φ∈(QT)应满足:
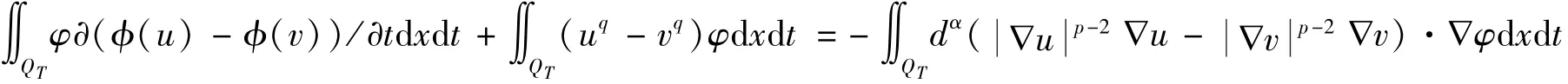
将任意固定的s∈[0,T],通过光滑化,选取X[0,s](u-v)作为以上等式的检验函数,其中X[0,s]是[0,s]上是特征函数.于是
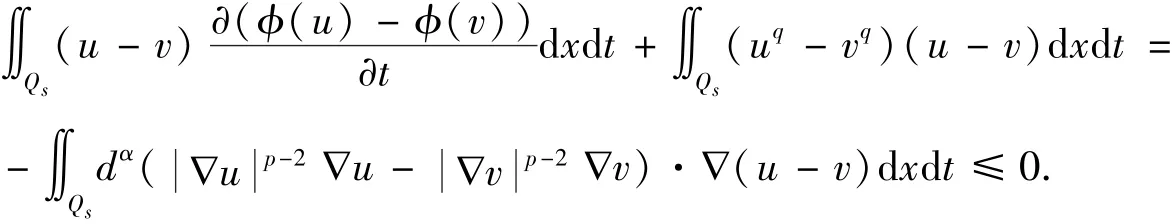


注意到φ∈C2,由微分中值定理,∃ξ∈Qs,使得φ(u)-φ(v)=φ′(ξ)(u-v).又φ′>0,由积分第一中值定理知,∃ξ0∈Qs,使得
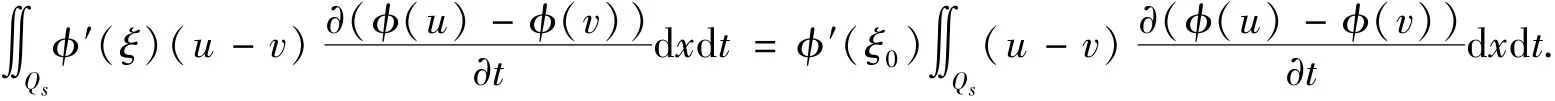
s)=v(x,s)对(x,s)∈QT几乎处处成立.
定理1得证.
2.2 定理2的证明
存在性已由引理1给出,以下证明唯一性.


成立.对任意固定s∈[0,T],通过光滑化,选取X[0,s]φ(u)-φ(v)ξε作为上式的检验函数,这里X[0,s]是[0,s]上的特征函数,即

由微分中值定理,∃ξ∈Qs,使得φ(u)-φ(v)=φ′(ξ)(u-v).又φ′>0,由积分第二中值定理知,存在ξ1,ξ2∈Qs,使得


从而
定理2得证.
[1]汤林冰.边界退化的非Newton多方渗流方程 [D].厦门:集美大学,2014.
[2]YIN J,WANG C.Properties of the boundary flux of a singular diffusion process[J].Chin Ann Math,2004,25B(2):175-182.
[3]WU Z,ZHAO J,YUN J.Nonlinear diffusion equations[M].New York:World Scientific Publishing,2001.
[4]KALASHIOKOW A S.Some problems of the qualitative theory of nonlinear degenerate second order parabolic equations[J].Russian Math Surveys,1987,42(2):169-222.
[5]谢清梅,詹华税.带有吸附项的边界扩散退化抛物方程解的性质 [J].集美大学学报:自然科学版,2012,17(1):71-74.
[6]伍卓群,赵俊宁.非线性扩散方程 [M].长春:吉林大学出版社,1996.
[7]ZHAN Hua-shui.Solution to nonlinear parabolic equation related to p-Laplacian[J].Chin Ann Math,2012,33(5):767-782.
[8]DIBENEDETTO E.Degenerate parabolic equations[M].New York:Spring-Verlag,1993.
[9]DAMBROSIO W.Multiple solutions of weakly-coupled systems with p-Laplacian operators[J].Results Math,1999,36(1/2):34-35.
Properties of Singular Solutions of the Doubly Degenerate〛Diffusion Equation with Adsorption
OUYANG Miao
(School of Applied Mathematics,Xiamen University of Technology,Xiamen 361000,China)

doubly degeneracy;diffusion equation;existence;uniqueness
O175.27
A
1673-4432(2015)05-0084-05
(责任编辑 李 宁)
2015-04-20
2015-09-21
欧阳苗 (1981-),女,讲师,硕士,研究方向为微分方程解的适定性.E-mail:mouyang@xmut. edu.cn

