基于函数驱动的随机混沌雷达波形设计

唐 骏，张 璘，袁江南

(厦门理工学院光电与通信工程学院,福建厦门361024)

基于函数驱动的随机混沌雷达波形设计

唐 骏，张 璘，袁江南

(厦门理工学院光电与通信工程学院,福建厦门361024)

针对噪声雷达信号源产生难的问题，提出一种基于函数驱动的混沌雷达波形设计方法.通过分析函数xn＝p（θTzn）和耦合不可逆变换的非线性映射之间的联系，理论上证明此类系统能产生不可预测的动力行为.据此原理可以构造出混沌系统，能产生真随机的混沌信号.仿真结果表明，该混沌信号及其频率调制信号都具有类δ的自相关函数，功率谱平坦，十分适合于宽带高分辨雷达的应用.

噪声雷达；混沌系统；波形设计；函数驱动；自相关；随机性

波形设计是雷达、声纳等探测系统的一个重要环节.波形不仅决定了系统的分辨率、测量精度、抗干扰能力以及目标跟踪性能等［1］,也影响到后续的信号处理方法.随机信号雷达具有 “图钉型”的模糊函数,距离、速度分辨率和测量精度高［2－3］,具有抗干扰能力强、截获概率低、电磁兼容性好等优点［4－5］.虽然随机噪声具有良好的相关特性,但产生、复制和控制都比较麻烦.因此,理想的噪声信号源难以获取,而常采用伪随机信号作为噪声雷达信号源.尽管混沌信号本身是确定性信号,但能表现出类噪声特性,被解释为确定性系统内在随机性的表现.混沌信号具有随机性强、样本容量大及相关性能优异等特点,与随机噪声相比,结构、参数和初值完全相同的混沌系统所产生的混沌信号完全相同,不仅易于产生,也具有更好的可控性和使用性,克服了随机码产生和存储不易、伪随机数量较少等不足.另外,由于混沌信号的初值敏感性和随机性,混沌调制雷达系统具有很强的抗干扰能力,使得混沌信号应用于雷达系统成为研究热点［6－7］.

基于现有的混沌系统已经设计出了性能优良的雷达波形,并通过混沌调制的方式得到了宽带雷达信号.但是,由于这些系统根本上是确定性的,从而决定了混沌信号的内在结构性和确定性,所设计的波形不具有严格意义的随机性,尤其经过不同方式调制之后,有些混沌信号的相关特性变得很差,甚至不能用做雷达信号.为了提高雷达波形的性能,很多研究从不同方面对现有的系统进行了改进：文献 ［8］对混沌信号进行抽取以降低样点之间的相关性；文献 ［9］将多个混沌系统进行结合；文献 ［10－11］基于对Lorenz系统参数的调节来设计波形；文献 ［12－13］通过对原有混沌系统进行修正以得到所期望的混沌序列.但是,这些改进方法既缺乏严格的系统化理论,也不具有普适性,更不是提高雷达波形性能的根本手段.以往混沌雷达波形设计是从众多的已知混沌系统中选择合适的系统,或调整系统参数以得到适于雷达应用的混沌信号,这一思路可以总结为由系统寻找混沌解.本文基于对混沌解的分析,反推混沌系统的特点,提出基于函数驱动的随机混沌雷达波形设计方法,从动力系统的构造角度出发,在统一的理论框架下构造随机混沌系统,对应的混沌信号具有随机性,克服了以往混沌系统内在确定性的缺陷.

1 确定系统的随机性

对于logistic映射

其中：n为自然数；Xn∈［0,1］,通常的做法是通过迭代来得到混沌序列.

事实上,文献 ［14－15］最先证明了

是Logistic的通解,n为自然数,θ为非零的实数.之后陆续发现许多混沌系统可以精确求解［16－18］.这些混沌解可以用式 (3)表示：

其中：P(·)是周期函数；T为周期；z为整数；P(θT)定义了初始值.由于方程描述的是一个确定性的过程,因此当z为整数时,式 (3)也是一个确定性的序列.然而,当z为非整数时,情况变得有所不同［19］.

设z是有理数,记为z＝p/q,其中p,q是互质的整数.可以证明,如果已知由方程产生的m＋1 (m为任意自然数)个点X0,X1,X2,…,Xm,不能预测下一个点Xm＋1的值.

定义由整数k参数化的序列

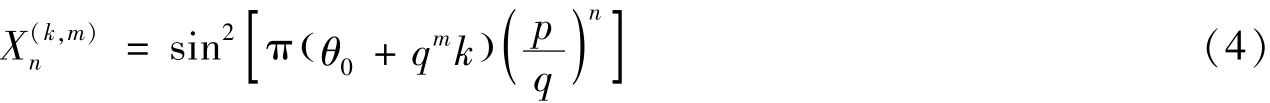
最初m＋1个点的值是相同的,这是因为

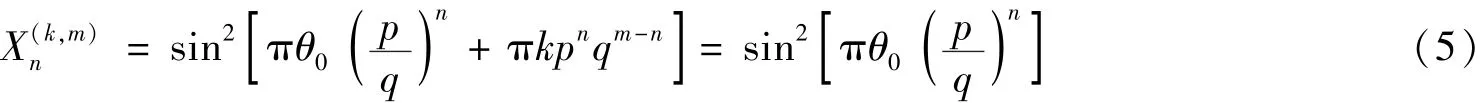
对所有n≤m成立.因此,有无穷多个序列的前m＋1个点的值相同 (因为k可以取无穷多个值,因此对应无穷多个序列).然而下一个点的值

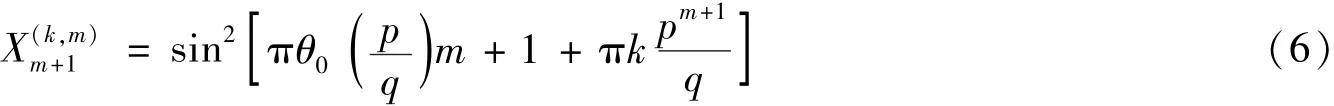
是不确定的,通常可以取q个不同的值,从而说明序列X(k,m)n是前向不可预测的.下面证明其也是后向不可预测的.

定义序列簇

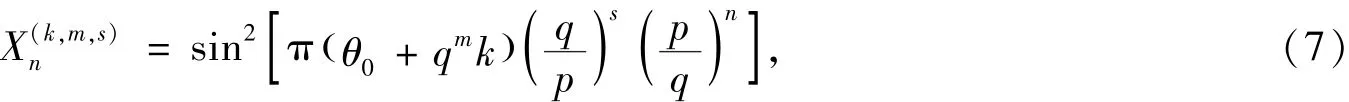
其中k,m,s都是整数.

对所有由k参数化的序列,由上述证明可知,已知m＋1个点Xs,Xs＋1,Xs＋2,…,Xs＋m的值,无法预测下一个点Xs＋m＋1的值,它可能有q种不同的取值.另一方面,从Xs,Xs＋1,Xs＋2,…,Xs＋m也无法确定Xs－1的值,因为

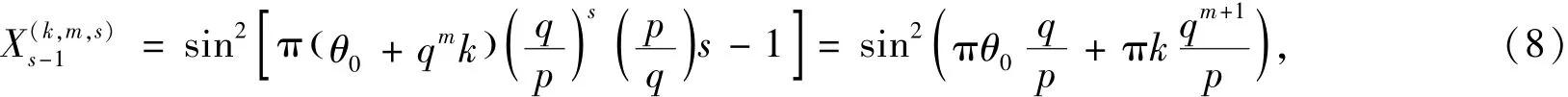
从而Xs－1有p种不同的可能取值.对于z为无理数的情况,过去和将来的点有无穷种可能的取值,因此,将来的点和过去的点的值都无法预测,这样的序列具有真随机性.

2 混沌信号的构造

通过对式 (3)产生随机行为的机理进行分析,如果写成一般形式：

则：f(n)为指数函数,h(y)为周期函数,分别对应混沌形成机理中的 “拉伸”和 “折回”,θ0为初始参数.如果f(n)为非周期函数,即使h(y)是周期的,序列Xn也不会是周期的.注意式 (3),当z＞1,zn随着n增大而增大,这给具体实现带来了麻烦.如果将n的值限定在合适的范围内,则可以通过非周期性地改变θ0的值,利用式 (9)来生成混沌序列.具体而言,在每生成N点长度的序列之后,改变θ0的值,n重新置为0.在每N点的序列之后,可以用如下的方法改变θ0的值：定义θs＝ACs,其中Cs可以由混沌系统产生,s代表θ0的序号,按这种方法,s＝1对应于第一个N点的序列段, s＝2对应于第二个N点的序列段,依此类推.系数A＞1是为了保证绝对不可预测性.这种情况下,通过观测Xn的值,不可能确定θ0的值.事实上,充分条件是θ0f(n)有界非周期振荡,在各振荡区间内具有有界的指数特性,许多混沌函数和伪周期函数都具有这些性质.

将上述思想推广到连续系统,可以构造形式上更为简单的混沌信号

其中：P(y)是周期函数；Q(t)是伪周期函数,因此,Aexp［Q(t)］满足有界非周期振荡,且在各振荡区间内具有有界的指数特性.根据式 (10),构造一个可以解析地求解Lyapuov指数的混沌函数

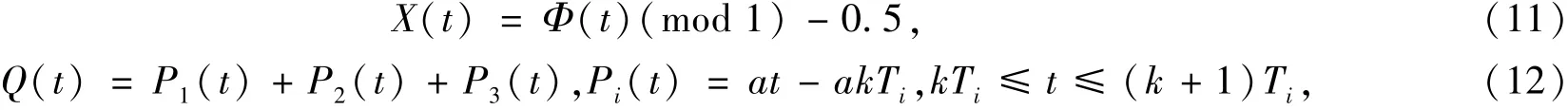
k为整数,比值T2/T1,T3/T2,T3/T1是无理数,则X(t)的Lyapunov指数理论值λ＝ln(3a).

针对式 (12),取参数a＝1,T1＝π,T2＝3＋2,T3＝3,X(t)波形如图1所示,Φ(0)分别为1.2和1.201 200 6,从图1中可以看出,随着时间的增长,初始值的微小改变,波形相差很大.用标准的数值方法计算产生的时间序列的Lyapunov指数,计算结果与理论值λ＝ln 3完全吻合.为了后续表述方便,X(t)记为Stochastic chaos信号.

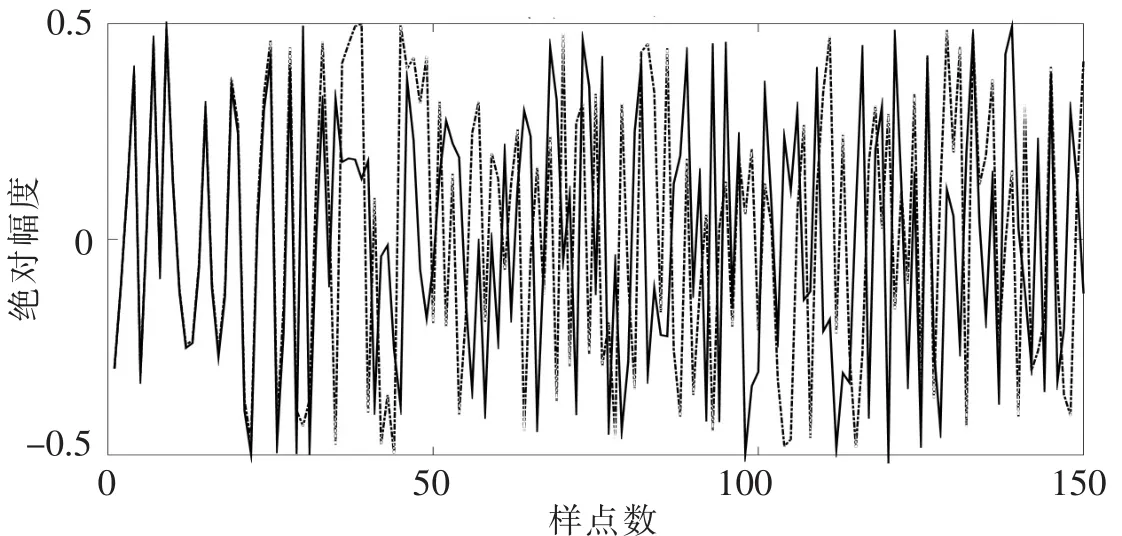
图1 随机混沌时域波形Fig.1 Waveform of stochastic chaos signal

3 雷达波形性能对比与分析

自相关函数和功率谱是雷达波形性能的重要指标,是决定雷达分辨率的主要因素.理想的雷达波形自相关函数应该是δ函数,功率谱是一条直线,实际中希望自相关函数有尽量尖锐的主瓣、尽量低的旁瓣,功率谱尽可能平坦,并以此来评价雷达波形性能的优劣.

由于混沌序列具有各态遍历性,对于一个足够长的混沌序列,可视为均值和方差为常量的随机变量,即混沌序列具有宽平稳特性,可以用时间平均来研究统计特性.对于一个具有遍历性和宽平稳的混沌序列,其自相关函数可定义为：

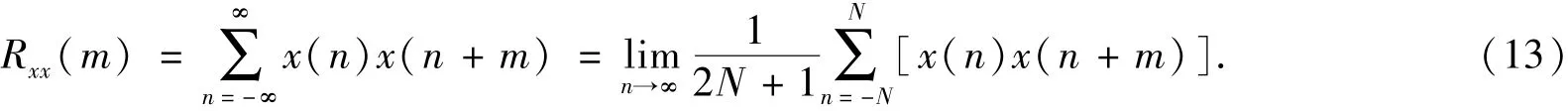
混沌序列功率谱是序列自相关函数的傅立叶变换,即

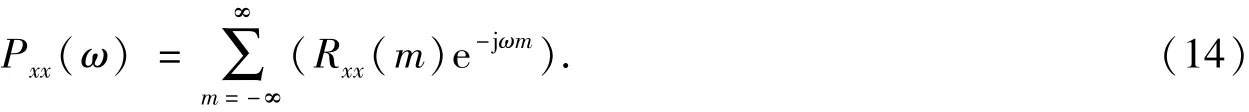
由于混沌序列的非周期性,不同初始值下的混沌序列自相关函数会略有波动,单次实现的混沌自相关不能准确反映系统的特性.因此,在分析自相关特性和功率谱时,常采用多次实现的平均值,利用基于均匀分布的M个不同初值产生的M个混沌序列的自相关函数进行平均,并由平均自相函数计算离散傅立叶变换,从而得到混沌序列的功率谱.仿真中,本文M＝200,每次实现取30 000个点.

为了全面考察和比较各雷达波形的性能,考虑了Logistic、Bernoulli和Lorenz 3类常见混沌系统,分别从原始序列及频率调制信号进行对比.各系统描述方程及仿真参数见表1.Logistic原始序列自相关及功率谱如图2所示,Logistic频率调制信号自相关及功率谱如图3所示,Bernoulli原始序列自相关及功率谱如图4所示.

表1 混沌系统及其参数Table 1 Chaotic systems and parameters

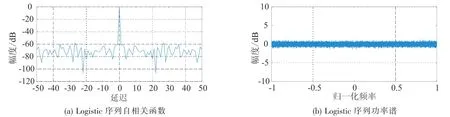
图2 Logistic原始序列自相关及功率谱Fig.2 ACF of Logistic sequence and power spectrum

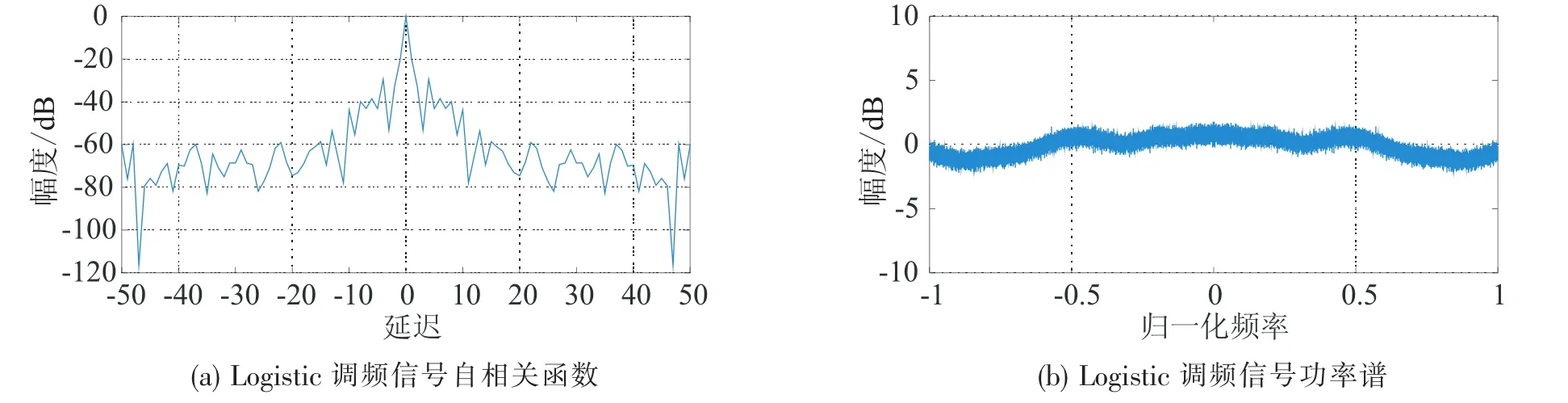
图3 Logistic调频信号自相关函数及功率谱Fig.3 ACF of Logistic FM and power spectrum

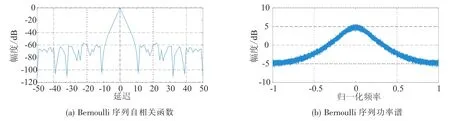
图4 Bernoulli序列自相关函数及功率谱Fig.4 ACF of Bernoulli sequence and power spectrum

Bernoulli频率调制信号自相关及功率谱如图5所示,Lorenzx(t)原始序列自相关及功率谱如图6所示,Lorenzx(t)频率调制信号自相关及功率谱如图7所示,Stochastic chaos原始序列自相关及功率谱如图8所示,Stochastic chaos频率调制信号自相关及功率谱如图9所示.

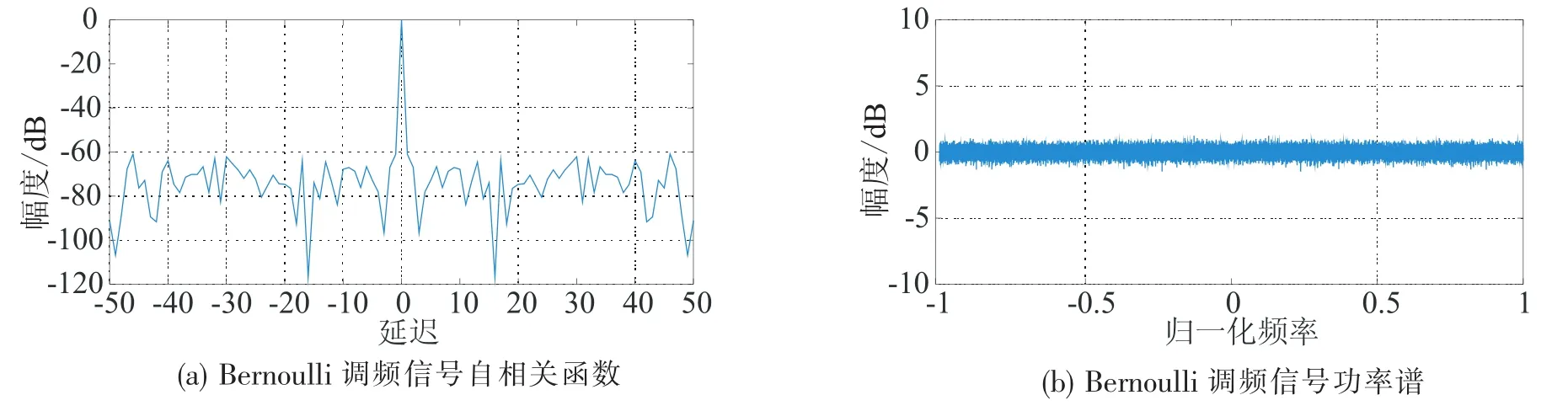
图5 Bernoulli调频信号自相关函数及功率谱Fig.5 ACF of Bernoulli FM and power spectrum

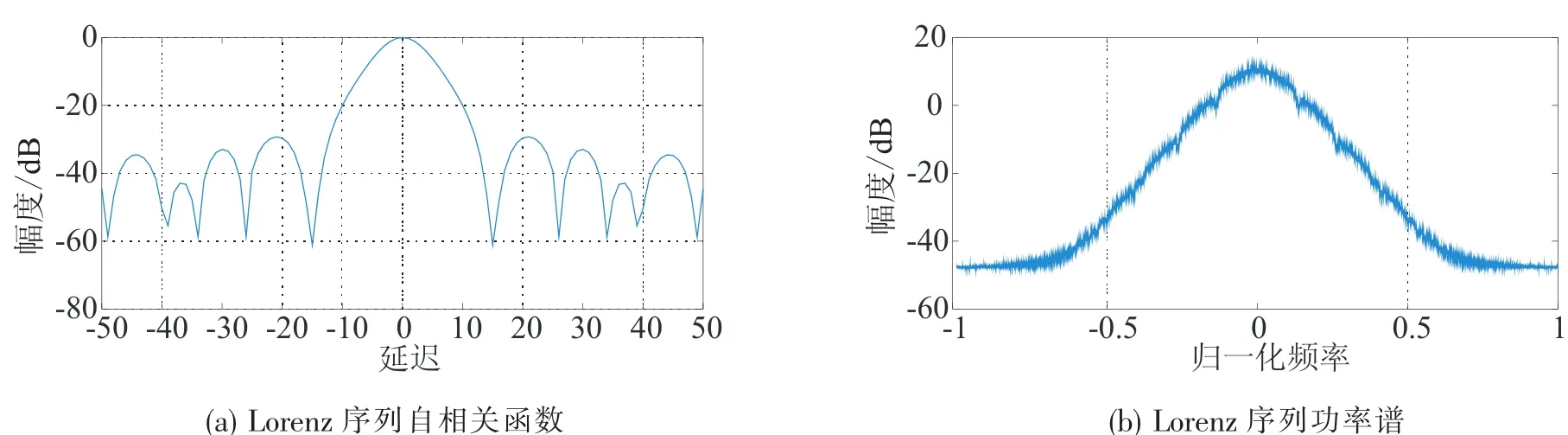
图6 Lorenz序列自相关函数及功率谱Fig.6 ACF of Lorenz sequence and power spectrum

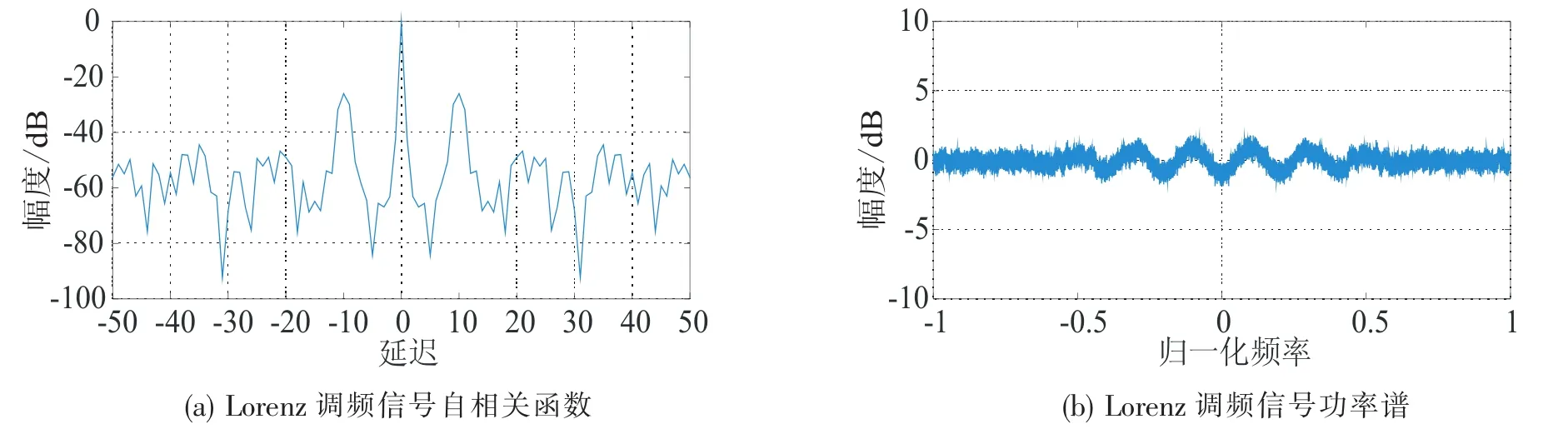
图7 Lorenz调频信号自相关函数及功率谱Fig.7 ACF of Lorenz FM and power spectrum

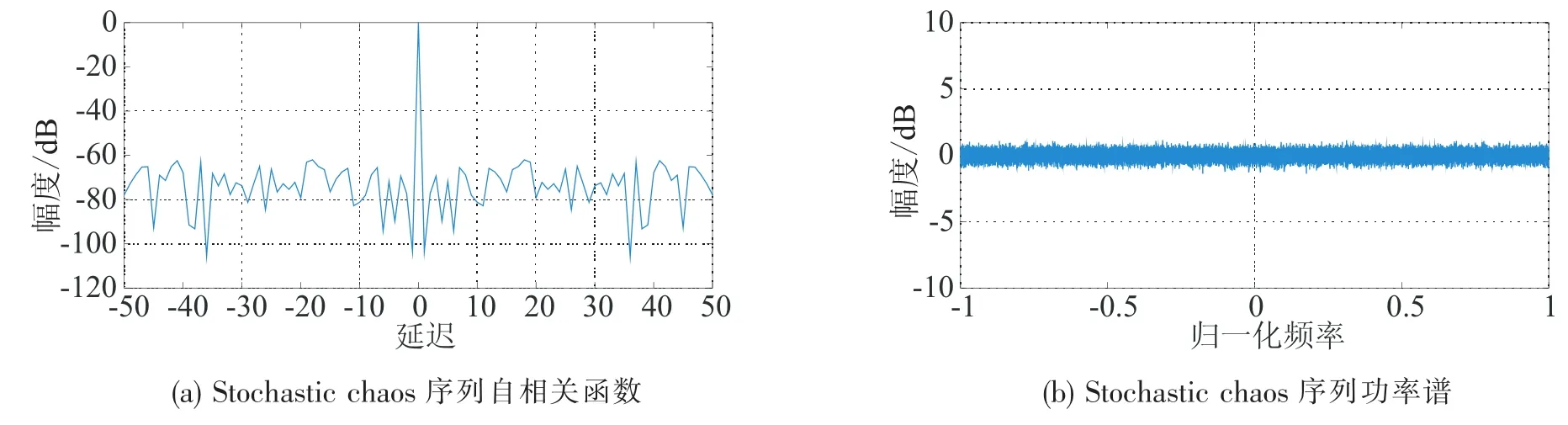
图8 Stochastic chaos序列自相关函数及功率谱Fig.8 ACF of Stochastic chaos sequence and power spectrum

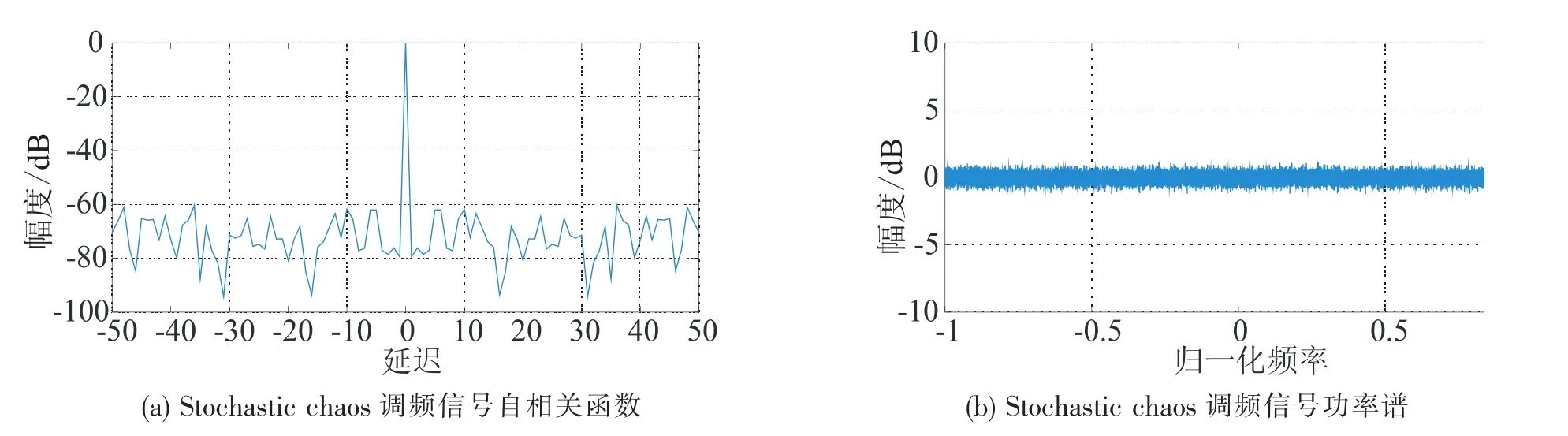
图9 Stochastic chaos调频信号自相关函数及功率谱Fig.9 ACF of Stochastic chaos FM and power spectrum

由图2和图3可以看出,Logistic原始序列的自相关函数性能较好,但经频率调制之后,自相关函数性能变差；图4和图5表明,Bernoulli原始序列的自相关特性较差,但经频率调制之后性能变好；图6和图7表明Lorenz序列自相关性能都不好；图8和图9表明,Stochastic chaos原始序列及频率调制之后都具有自相关函数尖锐、功率谱平坦的优点.

4 结语

熟知的几类混沌系统,由于解的内在确定性,基于这些系统所设计的波形不具有真正意义上的随机性,用作噪声雷达信号源时性能不尽理想,且受调制方式影响较大,因此不便于应用.本文基于已有的混沌解结构特点,从动力系统的构造角度出发,提出了基于函数驱动的随机混沌雷达波形设计方法,即用非周期函数驱动周期系统,在统一的理论框架下构造随机混沌信号,该信号具有真随机性,克服了以往混沌系统内在确定性的缺陷.随机混沌信号各样点的值具有完全不可预测性,其自相关函数近似δ函数,功率谱平坦,经调频之后,自相关函数依然具有主瓣窄、旁瓣低的优点,功率谱平坦,即波形性能不受调制方式的影响,因此,它是宽带高分辨雷达的理想信号源.

［1］HAYKIN S.Radar signal processing［J］.ASSP Magazine，1985，2（2）：2-18.

［2］LIU G S，GU H，ZHU X H.The present and the future of random signal radars［J］.IEEE Transaction on Aerospace and Electronic Systems Magazine，1997，12（10）：35-40.

［3］LIU G S，GU H，SU W M.Development of random signal radars［J］.IEEE Transactions on Aerospace and Electronic Systems，1999，35（3）：770-777.

［4］LIU G S，GU H，SU W M.Random signal radar-a winner in both the military and civilian operating environments［J］. IEEE Transactions on Aerospace and Electronic Systems，2003，39（2）：489-498.

［5］GARMATYUK D S，NARAYANAN R M.ECCM capabilities of an ultrawideband bandlimited random noise imaging radar［J］.IEEE Transactions on Aerospace and Electronic Systems，2002，38（4）：1 243-1 255.

［6］LEUNG H，LO T.Chaotic radar signal processing over the sea［J］.Oceanic Engineering，1993，18（3）：287-295.

［7］FLORES B C，SOLIS E A，THOMAS G.Chaotic signals for wideband radar imaging［C］//SPIE.International Society for Optics and Photonics.Orlando：SPIE，2002：100-111.

［8］YANG J，NIE L，QIU Z K，et al.Frequency modulated radar waveform based on sampled chaotic series［J］.Chinese Journal of Electronics，2013，22（2）：426-432.

［9］YANG Q L，ZHANG Y H，GU X.A signal model based on combination chaotic map for noise radar［J］.Progress In Electromagnetics Research，2013，28：57-71.

［10］PAPPU C S，FLORES B C.Generation of high-range resolution radar signals using the Lorenz chaotic flow［C］// SPIE.Defense，Security，and Sensing.International Society for Optics and Photonics.Orlando：SPIE，2010：12.

［11］WILLSEY M S，CUOMO K M，OPPENHEIM A V.Quasi-orthogonal wideband radar waveforms based on chaoticsystems［J］.IEEE Transactions on Aerospace and Electronic Systems，2011，47（3）：1 974-1 984.

［12］CHEN B.Improving autocorrelation and RFM autocorrelation performance of skew tent sequence［C］//NCIS.2011 International Conference on.Nanchang：IEEE，2011：298-301.

［13］XIE S B，HE Z S，HU J F，et al.Performances of improved tent chaos-based FM radar signal［J］.Journal of Systems Engineering and Electronics，2012，23（3）：385-390.

［14］STEIN P R，ULAM S M.Non-linear transformation studies on electronic computers［R］.Los Alamos：Los Alamos Scientific Lab，1962.

［15］ULAM S.John von Neumann 1903—1957［J］.Bulletin of the American Mathematical Society，1958，64（3）：1-49.

［16］UMENO K.Method of constructing exactly solvable chaos［J］.Physical Review E，1997，55（5）：5 280-5 284.

［17］GONZÁLEZ J A，PINO R.A random number generator based on unpredictable chaotic functions［J］.Computer Physics Communications，1999，120（2）：109-114.

［18］GONZALEZ J A，DE CARVALHO L B.Analytical solutions to multivalued maps［J］.Modern Physics Letters B，1997，11（12）：521-530.

［19］ GONZÁLEZ J A，PINO R.Chaotic and stochastic functions［J］.Physica A：Statistical Mechanics and its Applications，2000，276（3）：425-440.

Function-Driven Stochastic Chaotic Radar Waveform Design

TANG Jun，ZHANG Lin，YUAN Jiang-nan
（School of Opto-electronic and Communication Engineering，Xiamen University of Technology，Xiamen 361024，China）

A function-driven method was proposed of chaotic radar waveform design to solve the difficulty of noise radar signal source generation.The connections between functions of xn＝p（θTzn）and nonlinear maps coupled to non-invertible transformations were investigated.It was proved theoretically that these systems could produce unpredictable dynamics.According to this principle，we can construct chaotic system which can produce true stochastic chaotic signal.Simulation result suggested that this chaotic signal and frequencymodulated signal had-like autocorrelation function，and flat power spectrum，it is very suitable for wide band high resolution radar application.

noise radar；chaos system；waveform design；function-driven；autocorrelation；randomness

TN951

A

1673－4432（2015）05－0052－07

（责任编辑 雨 松）

2015－05－05

2015－07－13

国家自然科学基金项目 (61202013)；福建省教育厅科技项目 (JA13235)

唐骏 (1977－),男,讲师,博士研究生,研究方向为雷达信号处理.E-mail：jtang＠xmut.edu.cn