混合签密综述
俞惠芳, 杨 波, 张文政
(1. 陕西师范大学 计算机科学学院, 陕西 西安 710062;2. 青海师范大学 计算机学院, 青海 西宁 810008;3. 保密通信重点实验室, 四川 成都610041;4. 中国科学院信息工程研究所 信息安全国家重点实验室, 北京 100093)
混合签密综述
俞惠芳1,2,3,4, 杨 波1,3,4, 张文政3
(1. 陕西师范大学 计算机科学学院, 陕西 西安 710062;2. 青海师范大学 计算机学院, 青海 西宁 810008;3. 保密通信重点实验室, 四川 成都610041;4. 中国科学院信息工程研究所 信息安全国家重点实验室, 北京 100093)
混合签密中的签密KEM运用公钥技术封装一个对称密钥,DEM使用对称技术和KEM生成的对称密钥加密任意长度的消息。混合签密的安全模型允许其非对称部分和对称部分的安全需求完全独立,各自的安全性可以分别研究。和公钥签密技术相比,混合签密技术在密码学应用中具有更高的灵活性和安全性。文章对已有混合签密方案进行了深入的研究与分析,并给出了PKI环境下的混合签密、身份混合签密和无证书混合签密的算法模型、形式化安全定义和相应的实例方案。也指出了进一步研究的问题。
混合签密; PKI; 身份密码学;无证书环境
网络的飞速发展,电子商务、电子政务以及日常生活的信息化,信息安全的核心技术密码学得到很大发展。同时,在大量数据需要保密并认证通信的应用背景下,与密码学技术相伴的不同公钥认证方法下的混合签密技术具有了良好的应用前景。这说明现有公钥签密方案在很多情形下已经不能满足密码学应用需求。混合密码系统的研究最先是从混合加密方案着手的,混合加密需要考虑两种加密结构混合后加密的安全性。
混合加密起初是先用公钥加密方案加密对称密钥,再用该对称密钥加密真正的消息,此时的混合加密仅限于应用需求并没有进行形式化安全定义。直到2004年,Cramer和Shoup[1]才对混合加密的KEM-DEM结构进行了形式化安全定义。混合加密[2-6]的优势是可以实现大消息的安全保密通信。混合加密有完全独立的KEM和DEM组成[7]。KEM-DEM结构允许分别定义并研究KEM与DEM的安全需求,为了使整个混合加密达到某种安全水平,只要KEM和DEM分别达到相应的安全水平即可,这极大方便了混合结构的安全性分析。
2005年,Dent采用KEM-DEM结构提出了混合签密方案[8-9],并给出了方案的算法模型和形式化安全定义。混合签密体制中,非对称部分需要接收者的公钥和发送者的私钥作为输入,从而确保了所产生随机密钥的数据完整性,起到了签名的效果;对称部分则使用非对称部分产生的对称密钥加密任意长度的消息,保证了消息确实源自所声称的消息源。自混合签密提出以来一直是密码学界的一个重要研究方向。学者们经过研讨做了不少混合签密方面的工作[10-24],这些研究成果可以满足密码学领域的不同应用环境和应用需求。
2008年,刘志远等人[18]提出了一个RSA混合签密方案,以一种简单的方式提供了不可否认性,通信开销仅为一个RSA模长。同年,Tan[19]构造了标准模型下的签密KEM和签密tag-KEM。签密tag-KEM中嵌入了一个随机标签作为输入因子,避免了接收者直接通过密钥封装来恢复对称密钥,从而接收者不可能任意伪造所选择消息的密文。
2011年,Sun和Li[11]提出了一个具有多个接收者的身份签密KEM方案,并且在随机预言模型下给出了安全性证明。同年,Sun和Li又设计了一个仅仅使用了1次双线性对运算的无证书混合签密方案[20],虽然该方案是可否认的,但是大多数实际应用并不要求不可否认性。
2012年,Singh指出Li的身份混合签密方案[21]存在不足,它仅仅只是证明了不可区分性。在文献[25]的启示下,Singh提出了一个新的身份混合签密方案[10],也给出了详略得当的安全性证明。
2013年,Li等人[12]构造了一个内部安全的无证书混合签密方案,并且证明了方案满足适应性选择密文攻击下的保密性和适应性选择消息下的不可伪造性。同年,卢万谊等人[22]提出了一个前向安全的可公开验证的无证书混合签密方案,该方案不仅安全性强而且计算效率高。
2014年,黎忠文[23]提出了一种多方混合签密方案,比起传统方式,在有多个参与者的情况下,多方混合签密可以显著提高信息传输效率。多方混合签密适合应用于防火墙中。同年,Han等人[24]设计了一个无证书环境下的基于多变量的多接收者混合签密方案,并且在随机预言模型下给出了安全性证明。
由上面的国内外的研究成果可以看出,密码学界主要研究了基于证书的混合签密方案、身份混合签密方案和无证书混合签密方案。比起公钥签密,混合签密具有更高的效率和更好的灵活性,尤其是在需要大量数据保密并认证通信的情形下。事实上,如何设计不同公钥认证方法下的混合签密方案或具有不同特殊性质的混合签密方案以及如何证明所提方案的安全性的工作仍然没有完成,还在继续进行和完善中。可以说,针对混合签密方案及其可证明安全性理论的研究和讨论方兴未艾。
混合签密是公钥密码的一个扩展,也是一种重要的密码学技术。混合签密的思想看似简单,但是根据学者们的不同研究目的或者结合密码学中其它相关内容,混合签密的实现方式却又丰富多彩。混合签密提出至今已有十年的时间,在这段时间内,它不断地向不同方向延伸和发展。
1 PKI环境下的混合签密
1.1 算法模型
一般地,一个PKI环境下的混合签密方案的算法模型包含下面的三个概率多项式时间算法。
设置 给定一个安全参数k,私钥生成器运行该算法产生系统参数η=(G,p,q,g,n,H1,H2),并生成实体的私钥xi和公钥Pi。
签密 给定参数η、消息m、发送者的公私钥(Ps,xs)、接收者的公钥Pr,由发送者执行该签密算法,输出的是密文C。
解签密 给定参数η、密文C、发送者公钥Ps、接收者的公私钥(Pr,xr),由接收者执行该解签密算法。如果验证等式成立,接收者接受明文m。否则,接收者输出表示解签密失败的符号⊥。
1.2 安全模型定义
一个PKI环境下的混合签密方案[8]应该满足保密性和不可伪造性。可基于下面的安全模型对PKI环境下的混合签密方案的安全性给出随机预言模型下的安全性证明。在下面的安全模型中不允许进行发送者身份和接收者身份相同的询问。
为了证明PKI环境下的身份混合签密方案的保密性,我们采用适应性选择密文攻击下的不可区分性安全模型。具体的描述中,我们需要考虑下面挑战者Γ和敌手A之间进行的交互游戏。
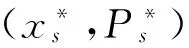
阶段1 在这个阶段,A执行如下多项式有界次适应性询问。每次的询问依赖于以前询问的应答。
签密询问 A在任何时候都能发出对消息m的签密询问。Γ从相关的“询问与应答”列表中检索到(xs,Ps,Pr),通过签密算法计算关于消息m的密文C,并将C发送给敌手。
解签密询问 A在任何时候都能发出对密文C的解签密询问。Γ从相关的“询问与应答”列表中检索到(xr,Ps,Pr),并运行解签密算法,然后将运行结果发送给敌手。
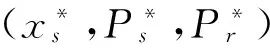
然后将挑战密文C*发送给敌手。

在敌手结束对交互游戏的执行的时候,输出一个猜测t*∈{0,1}。如果t*=t,则敌手攻击成功。敌手A获胜的优势可定义为安全参数k的函数,即
定义1.1(保密性) 如果任何多项式有界的敌手A赢得上述游戏的优势是可忽略的,则称一个PKI环境下的混合签密方案在适应性选择密文攻击下具有不可区分性。
为了证明PKI环境下的混合签密方案的不可伪造性,我们采用适应性选择明文攻击下的不可伪造性安全模型。具体的描述中,我们需要考虑下面挑战者Γ和伪造者F之间执行的交互游戏。
初始化 挑战者Γ输入安全参数k,运行设置算法得到系统参数。Γ发送系统参数给伪造者。
训练 在这个阶段,进行的“询问与应答”完全相同于定义1.1中的交互游戏的阶段1。
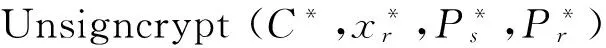
伪造者F获胜的优势可定义为它赢得交互游戏的概率。
定义1.2(不可伪造性) 如果任何多项式有界的伪造者F赢得上述游戏的优势是可忽略的,则称一个PKI环境下的混合签密方案在适应性选择消息攻击下具有不可伪造性。
1.3 实例方案
本节给出了一个PKI环境下的混合签密实例方案[8],它的三个概率多项式算法模块描述如下。
(1) 设置
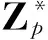
均是密码学安全的杂凑函数,在这里n是DEM的密钥长度。可信机构选择一个随机数
xs∈{1,2,…,q},
计算发送者的公钥
Ps=gxs;
另选择一个随机数
xr∈{1,2,…,q},
计算接收者的公钥
Pr=gxr。
可信机构公开系统参数(G,p,q,g,n,H1,H2)。
(2) 签密
给定消息m、发送者的公私钥(Ps,xs)和接收者的公钥Pr,发送者执行下列步骤。
(A1) 选择一个随机数t∈{1,2,…,q}。
(A3) 计算R=H1(m‖X)。
(A4) 计算S=t/(R+xs)。
(A5) 计算κ=H2(X)。
(A6) 计算c= DEM.Enc (κ,m)。
(A7) 设置C= (c,R,S)。
(A8) 输出密文C。
(3) 解签密
给定密文C、发送者的公钥Ps和接收者的公私钥(Pr,xr),接收者执行下列步骤。
(B1) 计算X= (Ps·gR)S·xrmodp。
(B2) 计算κ=H2(X)。
(B3) 计算m= DEM.Dec (κ,c)。
(B4) 检查验证等式R=H1(m‖X)是否成立?如果成立,接受明文m;否则,输出符号⊥。
2 身份混合签密
2.1 算法模型
一般地,一个身份混合签密方案的算法模型包含四个概率多项式时间算法:设置算法、密钥产生算法、签密算法和解签密算法。算法模型中涉及三个参与方:一个私钥生成器、一个身份为Ia的发送者以及一个身份为Ib的接收者。
设置 给定一个安全参数k,私钥生成器运行该设置算法产生系统参数η和主密钥x。在这里η是公开的,但是x保密的。
用户钥生成 给定(η,x,Ii),私钥生成器执行该用户钥生成算法,输出的是实体的私钥si和公钥yi。
签密 给定η、消息m、发送者的身份Ia和公私钥(ya,sa)、接收者的身份Ib和公钥yb,由发送者执行该签密算法,输出的是密文C。
解签密 给定η、密文C、发送者的身份Ia和公钥ya、接收者的身份Ib和公私钥(yb,sb),由接收者执行该解封装算法。如果验证等式成立,接收者接受明文m;否则,接收者输出表示解签密失败的符号⊥。
2.2 安全模型定义
一个身份混合签密方案[10]应该满足保密性和不可伪造性。可基于下面的安全模型对身份混合签密方案的安全性给出随机预言模型下的安全性证明。在下面的安全模型中不允许进行发送者身份和接收者身份相同的询问。
为了证明身份混合签密方案的保密性,我们采用适应性选择密文攻击下的不可区分性安全模型。具体的描述中,我们需要考虑下面挑战者Γ和敌手A之间进行的交互游戏。
初始化 挑战者Γ输入安全参数k,运行设置算法得到系统参数η和主密钥x。Γ发送η给敌手,但是保密x。
阶段1 在这个阶段,A执行如下多项式有界次适应性询问。
私钥询问 A在任何时候都能发出对身份Ii的私钥询问。Γ运行用户钥生成算法,然后将作为结果的私钥si发送给敌手。
签密询问 A在任何时候都能发出对消息m、发送者身份Ia和接收者身份Ib的签密询问。Γ从相关的“询问与应答”列表中检索到(sa,Pa,Pb),计算
C← Signcrypt (η,Ia,Ib,m,sa,Pa,Pb),
然后将密文C发送给敌手。
解签密询问 收到密文C、发送者身份Ia和接收者身份Ib的解签密询问时,Γ从相关的“询问与应答”列表中检索到(sb,Pa,Pb),计算
m/⊥ ← Unsigncrypt (η,Ia,Ib,C,sb,Pa,Pb),
然后将运行结果发送给敌手。

然后将密文C*发送给敌手。
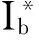
在敌手结束对交互游戏的执行的时候,输出一个猜测t*∈{0,1}。若t*=t,则敌手攻击成功。敌手获胜的优势可定义为安全参数k的函数,即
定义2.1(保密性) 如果任何多项式有界的敌手A赢得上述游戏的优势是可忽略的,则称一个身份混合签密方案在适应性选择密文攻击下具有不可区分性。
为了证明身份混合签密方案的不可伪造性,我们采用适应性选择明文攻击下的不可伪造性安全模型。具体的描述中,我们需要考虑下面挑战者Γ和伪造者F之间执行的交互游戏。
初始化 挑战者Γ输入安全参数k,运行设置算法得到系统参数η和主密钥x。Γ发送η给伪造者F,但是保留x。
训练 在这个阶段,进行的“询问与应答”完全相同于定义2.1中的交互游戏的阶段1。

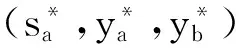
伪造者F获胜的优势可定义为它赢得交互游戏的概率。
定义2.2(不可伪造性) 如果任何多项式有界的伪造者F赢得上述游戏的优势是可忽略的,则称一个身份混合签密方案在适应性选择消息攻击下具有不可伪造性。
2.3 实例方案
本节给出了一个身份混合签密实例方案[10]。下面是它的四个概率多项式算法模块组成。
(1) 设置
设q是一个k比特的大素数,G1是阶为q的加法循环群,G2是相同阶的乘法循环群,P∈G1是群G1的一个生成元,e:G1×G1→G2是一个双线性映射。函数
H1: {0,1}*→ G1,H2: G2→ {0,1}n,H3: {0,1}*×G2→ Zq,
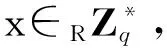
最后,私钥生成器保密主密钥,但公开系统参数
η=(G1,G2,e,P,Pput,n,H1,H2,H3)。
(2) 用户钥生成
已知(η,s),私钥生成器计算身份是Ia的发送者的公钥ya=H1(Ia)和私钥sa=xya,并计算身份是Ib的发送者的公钥yb=H1(Ib)和私钥sb=xyb。
(3) 签密
已知(η,m,Ia,Ib,sa,yb),发送者通过执行下面的步骤生成密文C。
(C2) 计算yb=H1(Ib)。
(C3) 计算κ1=e(P,Ppub)u。
(C4) 计算κ2=H2(e(Ppub,yb)u)。
(C5) 计算κ= (κ1,κ2)。
(C6) 计算c= DEM.Enc (κ2,m)。
(C7) 计算r=H3(m,κ1)。
(C8) 计算S=uPpub-rsa。
(C9) 输出密文C= (c,r,S)。
(4) 解签密
已知(η,C,Ia,Ib,sb,ya),接收者执行下列步骤。
(D1) 计算ya=H1(Ia)。
(D2) 计算κ1=e(P,S)e(Ppub,ya)r。
(D3) 计算κ2=H2(e(S,yb)e(ya,sb)r)。
(D4) 计算κ= (κ1,κ2)。
(D5) 计算m= DEM.Dec (κ2,c)。
(D6) 验证等式r=H3(m,κ1)是否成立?如果成立,接受明文m;否则,输出符号⊥。
3 无证书混合签密
3.1 算法模型
一个无证书混合签密方案的算法模型[17]可以通过以下六个概率多项式时间算法来定义。
设置 由密钥生成中心完成该设置算法。已知一个安全参数k,这个算法输出的是系统参数ρ和主密钥x。在这里ρ是公开的,但是x是保密的。
用户钥产生 由身份为Ii的用户完成该用户钥生成算法。已知用户身份Ii,这个算法输出的是该用户的秘密值xi和公钥Pi。
部分钥产生 由密钥生成中心完成该部分私钥生成算法。已知(ρ,x,Ii),这个算法输出的是身份为Ii的用户的部分私钥di。
私钥提取 由身份为Ii的用户完成该私钥提取算法。已知身份为Ii的用户的部分私钥di和秘密值xi,这个算法输出的是该用户的完整私钥
si=(xi,di)。
签密 由身份为Ia的发送者完成该签密算法。已知(ρ,Ia,Ib,m,Pa,sa,Pb),这个算法输出的是一个密文C。
解签密 由身份为Ib的接收者完成该解签密算法。已知(ρ,Ia,Ib,C,Pa,sb,Pb),接收者根据验证等式是否成立决定输出明文m还是表示解签密失败的标志⊥。
3.2 安全模型定义
无证书混合签密方案的安全模型[17]中不允许进行发送者身份和接收者身份相同的询问。可基于下面的安全模型对无证书混合签密方案的安全性给出随机预言模型下的安全性证明。
为了证明无证书混合签密方案的安全性,需要考虑两种类型的攻击者。在这里第1类攻击者AI或FI不知道密钥生成中心的主密钥,但是AI或FI能自适应地替换任意用户的公钥。第2类攻击者AII或FII知道密钥生成中心的主密钥,但是AII或FII不具备替换任意用户公钥的能力。
定义3.1(保密性)[17]如果任何多项式有界的敌手AI(相应的AII)赢得游戏I(相应的游戏II)的优势是可忽略的,则称一个无证书混合签密方案在自适应选择密文攻击下具有不可区分性。
游戏I 这是挑战者Γ和敌手AI之间进行的一个交互游戏。
初始化 Γ运行Setup(1k)得到系统参数ρ和主密钥x。Γ将ρ发送给敌手Ai,但是保留x。
阶段1 在这个阶段,AI执行如下多项式有界次适应性询问。
公钥询问 AI在任何时候都可以请求身份Ii的公钥。Γ运行用户钥生成算法,然后把生成的公钥Pi发送给敌手。
部分私钥询问 AI在任何时候都可以请求身份Ii的部分私钥询问。Γ运行部分钥生成算法,然后把得到的部分私钥di发送给敌手。
私钥询问 AI在任何时候都可以请求身份Ii的私钥询问。Γ从相关的“询问与应答”列表中查找到含有关于身份Ii的秘密值xi和部分私钥di的条目,然后返回完整私钥si=(xi,di)给敌手。如果身份Ii的公钥已经被替换了,那么敌手不能询问该身份的秘密值。
公钥替换 AI可以在合适的范围内选择任意值替换任意身份的公钥。
签密询问 AI在任何时候都可以执行关于消息m、发送者身份Ia和接收者身份Ib的签密询问。Γ从相关的“询问与应答”列表中查找到(sa,Pa,Pb),计算
C← Signcrypt (ρ,Ia,Ib,m,sa,Pa,Pb),
然后返回密文C给敌手。
解签密询问 AI在任何时候都可以进行关于密文C、发送者身份Ia和接收者身份Ib的解签密询问。Γ从相关的“询问与应答”列表中查找到(sb,Pa,Pb),计算
m/⊥ ← Unsigncrypt (ρ,Ia,Ib,C,sb,Pa,Pb),
然后返回运行结果给敌手。

然后将密文C*发送给敌手AI。
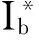
敌手AI结束对交互游戏的执行的时候,输出一个猜测γ*。如果γ*=γ,说明AI攻击成功。我们定义敌手AI的获胜优势为
游戏II 这是挑战者Γ和敌手AII之间进行的一个交互游戏。
初始化 Γ运行Setup(1k)得到系统参数ρ和主密钥x。Γ将(ρ,x)发送给敌手AII。
阶段1 在这个阶段,AII执行如下多项式有界次适应性询问。在这里敌手知道系统主密钥x,可以自己计算出用户的部分私钥。
公钥询问 AII在任何时候都可以请求身份Ii的公钥询问。Γ运行UserGen(Ii),然后返回生成的公钥Pi给敌手。
私钥询问 AII在任何时候都可以请求身份Ii的私钥询问。Γ从相关的“询问与应答”列表中查找到含有关于身份Ii的秘密值xi和部分私钥di的条目,然后返回完整私钥si=(xi,di)给敌手。
签密询问 AII在任何时候都可以进行关于消息m、发送者身份Ia和接收者身份Ib的签密询问。Γ从相关的“询问与应答”列表中查找到(sa,Pa,Pb),计算
C← Signcrypt (ρ,Ia,Ib,m,sa,Pa,Pb),
然后返回密文C给敌手。
解签密询问 AII在任何时候都可以进行关于密文C、发送者身份Ia和接收者身份Ib的解签密询问。Γ从相关的“询问与应答”列表中查找到(sb,Pa,Pb),计算
m/⊥ ← Unsigncrypt (ρ,Ia,Ib,C,sb,Pa,Pb),
然后返回运行结果给敌手。

然后将密文C*发送给敌手。
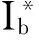
敌手AII结束对交互游戏的执行的时候,输出一个猜测γ*。如果γ*=γ,说明AII攻击成功。我们定义敌手AII的获胜优势为
定义3.2(不可伪造性)[17]如果任何多项式有界的伪造者FI(相应的FII)赢得游戏I′(相应的游戏I′)的优势是可忽略的,则称一个无证书混合签密方案在自适应选择明文攻击下具有不可伪造性。
游戏I′ 这是挑战者Γ和伪造者FI之间进行的一个交互游戏。
初始化 Γ运行Setup(1k)获得系统参数ρ和主密钥x,然后返回ρ给攻击者FI,但是保留x。
训练 在这个阶段,FI执行多项式有界次适应性询问。FI所进行的询问以及相关应答和游戏I的阶段1相同。
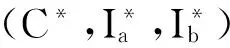
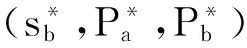
我们定义伪造者FI获胜的优势为FI赢得游戏I′的概率。
游戏II′ 这是挑战者Γ和伪造者FII之间进行的一个交互游戏。
初始化 Γ运行Setup(1k)得到系统参数ρ和主密钥x,然后将(ρ,x)发送给伪造者FII。
训练 在这个阶段,FII执行多项式有界次适应性询问。FII所进行的询问以及相关应答和游戏II的阶段1完全相同。
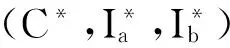
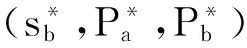
我们定义伪造者FII获胜的优势为FII赢得游戏II′的概率。
3.3 实例方案
本节给出了一个无证书混合签密实例方案[17]。下面是它的六个概率多项式算法模块组成。
(1) 设置
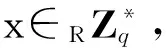
密钥生成中心选择三个密码学安全的杂凑函数
在这里n是DEM的对称密钥长度。
最后,密钥生成中心保密主控钥x,但公开系统参数
ρ=(G1,G2,e,P,Ppub,n,H1,H2,H3)。
(2) 部分钥产生
已知(ρ,x),密钥生成中心计算身份为Ii的用户的部分私钥di=xFi,在这里Fi=H1(Ii)。然后发送(Ii,di)给用户。
(3) 用户钥产生
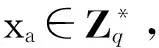
(4) 私钥提取
已知身份为Ii的用户的部分私钥di和秘密值xi,那么该用户的完整私钥是si←(xi,di)。
(5) 签密
已知ρ、消息m、发送者的身份Ia和公私钥(Pa,sa)、接收者的身份Ib和公钥Pb,发送者执行下面的步骤生成密文C。
(E2) 计算R=rP。
(E3) 计算y=e(Ppub,Fb)r。
(E4) 计算z=e(Pb,Fb)r。
(E5) 计算κ=H2(y,z,R)。
(E6) 计算c= DEM.Enc (κ,m)。
(E7) 计算f=H3(Ia,Ib,m,R,Pa,Pb)。
(E8) 计算S=rFa+xaf+da。
(E9) 输出C= (c,R,S)。
(6) 解签密
已知ρ、密文C、发送者的身份Ia和公钥Pa、接收者的身份Ib和公私钥(Pb,sb),接收者执行下面的步骤。
(F1) 计算y=e(R,db)。
(F2) 计算z=e(R,Hb)xb。
(F3) 计算κ=H2(y,z,R)。
(F4) 计算m= DEM.Dec (κ,c)。
(F5) 计算f=H3(Ia,Ib,m,R,Pa,Pb)。
(F6) 如果成立
e(P,S)=e(R,Fa)e(Pa,f)e(Ppub,Fa),
则接受明文m;否则,输出符号⊥。
4 后续工作展望
混合密码系统不仅是对称密码和公钥密码的简单组合,而且可以看作是公钥密码系统的一个分支。混合签密是新兴起的混合密码学技术。虽然目前我们取得了一些混合签密方面的研究进展,但是应该说研究工作还远远没有停止,尤其离在现实场景中的实践应用还存在着很大的差距。不同公钥认证方法下的混合签密以及具有特性的混合签密的方案设计、形式化安全定义和相关的可证明安全性理论研究还需要进一步完善和继续深入研究。实际应用环境中的解决方案更加需要继续深入研究。
(1) 椭圆曲线混合签密方案研究
这类方案的设计是混合密码学的研究重点,因为这类方案可以解决有限资源环境(比如,无线传感器网络、ad hoc网络、mesh网络或智能卡)中传输的数据的安全性问题。
(2) 没有随机预言机的混合签密方案研究
现有混合签密方案绝大多数都是基于随机预言模型的。但是随机预言模型下的安全性在真实环境中不一定能得以保证。虽然普遍认为标准模型下的密码方案计算效率比较低,但是在真实环境下标准模型中的安全性能得以保证。因此,设计标准模型下的可证明安全的混合签密方案是下一步的重要研究内容。
(3) 通用可复合安全的混合签密方案研究
复合安全需要保证某个密码方案在独立计算情况下是安全的,在复杂的网络环境中这个密码方案运行的多个实例仍然是安全的,这个密码方案作为其他方案的组件,通过复合操作构成的大型方案仍然安全的。然而,在通用可复合安全框架下提出的通用可复合安全的混合签密方案目前很少见到相关报道,而实际的情况是,在复杂的网络和分布式环境下许多在孤立模型中安全的单个密码方案与其他密码方案组合后,根本无法保证组合以后形成的复杂方案的安全性。构造通用可复合安全的混合签密方案的的理想功能并且通过理想功能设计通用可复合安全的相应密码方案是很重要的研究内容。
(4) 网络编码环境下的混合签密方案研究
在无线ad-hoc网络、无线传感器网络等环境中,采用网络编码可以极大地节省网络资源和提高网络传输速率、吞吐量和可靠性。但作为一种有着广泛应用前景的新技术,网络编码发展不得不面临污染和窃听等安全威胁。攻击者可以通过节点蓄意地篡改或伪造消息,这些被篡改或伪造的消息与其它消息进行线性组合后,会污染其它消息;而且攻击者通过窃听网络中的部分或者全部信道来获取网络中传输的消息。这些不安全因素在很大程度上限制了网络编码的应用范围,阻碍了网络编码在实践中的应用和推广。
针对网络编码应用中存在的污染和窃听攻击降低网络编码传输效率的问题,设计高效实用的网络编码混合签密方案对于网络编码发展显得尤为重要。目前编码环境下的混合签密方案甚少。鉴于混合签密技术在信息安全领域中的广泛应用,在双线性映射、离散对数和椭圆曲线及其安全假设的理论基础上,设计不同真实场景的网络编码混合签密是下一步研究的重要内容。
5 结束语
本文回顾了关于混合签密的国内外研究情况,给出了PKI环境下的混合签密、身份混合签密和无证书混合签密的算法模型、安全模型定义和相应实例方案。进而给出了将来的研究计划。
[1] Cramer R, Shoup V. Design and analysis of practical public-key encryption schemes secure against adaptive chosen ciphertext attack[J]. SIAM Journal on Computing, 2004, 33(1): 167-226.
[2] Abe M, Gennaro R, Kurosawa K. Tag-KEM/DEM: a new framework for hybrid encryption[J]. Journal of Cryptology, 2008(21): 97-130.
[3] Kurosawa K, Desmedt Y. A new paradigm of hybrid encryption scheme[C]//Proceedings of the 24th Annual International CryptologyConference. Santa Barbara, California, USA, 2004: 426-442.
[4] Fujisaki E, Okamoto T. Secure integration of asymmetric and symmetric encryption schemes[C]//Proceedings of CRYPTO’99, Lecture Notes in Computer Science Volume 1666, 1999: 537-554.
[5] Huang Q, Wong D. Generic certificateless encryption secure against malicious-but-passive KGC Attacks in the Standard Model[J]. Journal of Computer Science and Technology, 2010, 25(4): 807-826.
[6] 李继国, 杨海珊, 张亦辰. 带标签的基于证书密钥封装机制[J]. 软件学报, 2012, 23(8):2163-2172.
[7] 赖欣. 混合密码体制的理论研究与方案设计[D]. 西安: 西安交通大学, 2005.
[8] Dent A. Hybrid signcryption schemes with insider security[C]//Proceedings ofthe 10th Australasian Conference on Information Security and Privacy,Lecture Notes in Computer ScienceVolume 3574, Brisbane, Australia, 2005: 253-266.
[9] Dent A. Hybrid signcryption schemes with outsider security[C]//Proceedings ofthe 8th International Information Security Conference,Lecture Notes in Computer ScienceVolume 3650, Singapore, 2005: 203-217.
[10] Singh K. Identity-based hybrid signcryption revisited[C]//Proceedings of the 2012 International Conference on Information Technology and e-Services, Washington, 2012:34-39.
[11] Sun Y X, Li H. ID-based signcryption KEM to multiplerecipients[J]. Chinese Journal of Electronics, 2011, 20(2): 317-322.
[12] Li F G, Shirase M, Takagi T. Certificateless hybrid signcryption[J]. Mathematical and Computer Modelling, 2013, 57(3/4):324-343.
[13] Li X X, Qian H F, Yu Y, et al.. Constructing practical signcryption KEM from standard assumptions without random oracles[C]//Proceedings of Applied Cryptography and Network Security, Lecture Notes in Computer ScienceVolume 7954, 2013: 186-201.
[14] 赖欣, 黄晓芳, 何大可. 基于身份的高效签密密钥封装方案[J]. 计算机研究与发展, 2009, 45(6): 857-863.
[15] 张串绒, 张玉清. 可证明安全签密方案及其混合结构[J]. 西安电子科技大学学报:自然科学版, 2009, 36(4): 756-760.
[16] Yu H F, Yang B, Zhao Y, et al. Tag-KEM for self-certified ring signcryption[J]. Journal of Computational Information Systems, 2013, 9(20): 8061-8071.
[17] 俞惠芳, 杨波. 可证安全的无证书混合签密[J]. 计算机学报, 2015, 38(4): 804-813.
[18] 刘志远, 王小非, 崔国华, 等. 一种基于RSA的混合签密方案[J]. 华中科技大学学报:自然科学版, 2008, 36(1): 49-51.
[19] Tan C. Insider-secure signcryption KEM/Tag-KEM schemes without random oracles[C]//Proceedings of the third International Conference on Availability, Reliability and Security-ARES 2008, Barcelona, Spain, 2008: 1275-1281.
[20] 孙银霞, 李晖. 高效无证书混合签密[J]. 软件学报, 2011, 22(7): 1690-1698.
[21] Li F G, Masaaki S, Tsuyushi T. Identity-based hybrid signcryption[C]// Proceedings of the 2009 International Conference on Availability, Reliability and Security, 2009: 534-539.
[22] 卢万谊, 韩益亮, 杨晓元, 等. 前向安全的可公开验证无证书混合签密方案[J]. 小型微型计算机系统, 2013, 34(12): 2814-2817.
[23] 黎忠文, 黎仁峰, 钟迪, 等. 一个高效的多方混合签密方案[J]. 科学技术与工程, 2014, 14(17): 83-87.
[24] Han Y L, Yue Z L, Fang D Y, et al. New multivariate-based certificateless hybrid signcryption scheme for multi-recipient[J]. Wuhan University Journal of Natural Sciences, 2014, 19(5): 433-440.
[25] Libert B, Quisquater J J. New identity based signcryption schemes from pairings[C]//Proceedings of the IEEE Information Theory Workshop,IEEE Information Theory Society, 2003: 155-158.
[责任编辑:陈文学]
A survey of hybrid signcryption
YU Huifang1,2,3,4, YANG Bo1,3,4, ZHANG Wenzheng3
(1. School of Computer Science, Shaanxi Normal University, Xi’an 710062, China; 2. School of Computer, Qinghai Normal University, Xining 810008, China; 3. Communication Security Laboratory on Science and Technology, Chengdu 610041, China; 4. State Key Laboratory of Information Security, Chinese Academy of Sciences, Beijing 100093, China)
In hybrid signcryption, a signcryption key encapsulation mechanism (KEM) employs the public key technique to encapsulate a symmetric key, while a data encapsulation mechanism (DEM) makes use of the symmetric technique and symmetric key to encrypt arbitrary message. The security model of hybrid signcryption does have the advantage of allowing the security requirements of the asymmetric part and symmetric part to be completely independent, hence, we can study their security respectively. Compared with signcryption technique in public key setting, hybrid signcryption technique has higher flexibility and better security in cryptographic applications.We research and analyze the existing hybrid signcryption schemes, and then give the algorithm models, formally secure definitions and instance schemes for PKI-based hybrid signcryption, identity-based hybrid signcryption and certificateless hybrid signcryption. Moreover, we point out some possible future work.
hybrid signcryption, public key infrastructure, identity-based cryptography, certificateless
2015-04-12
国家自然科学基金资助项目(61363080, 61272436); 中国科学院信息工程研究所信息安全国家重点实验室开放课题资助项目(2015-MS-10);保密通信重点实验室基金资助项目(9140C110206140C11050)
俞惠芳(1972-), 女, 博士研究生, 副教授,从事密码学与信息安全研究。E-mail:yuhuifang@qhnu.edu.cn 杨波(1963-),男, 博士,陕西省“百人计划”特聘教授,博士生导师,从事密码学与信息安全研究。E-mail:byang@snnu.edu.cn
10.13682/j.issn.2095-6533.2015.03.001
TP309
A
2095-6533(2015)03-0001-10

