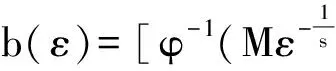独立同分布序列部分和之和精确渐近性的一般形式

邹广玉

(长春工程学院 理学院，吉林 长春 130012)

独立同分布序列部分和之和精确渐近性的一般形式

邹广玉

(长春工程学院 理学院，吉林 长春 130012)

利用独立同分布序列部分和之和的渐近性质,得到其精确渐近性的一般形式，丰富了独立同分布序列精确渐近性的结果。

独立同分布序列；部分和之和；精确渐近性

“部分和之和”的极限理论起源于Resnick[1]和Arnold等[2]对记录值分布的研究，在时间序列分析、破产理论等领域有着广泛应用，很多学者对其极限性质进行了研究。如文献[3]研究了独立同分布随机变量序列部分和之和的大数定律和中心极限定理，文献[4]研究了同分布NA随机变量序列部分和之和的强大数定律，文献[5]讨论了独立同分布序列部分和之和的完全收敛性等等,文献[6]研究了NA序列部分和之和大数定律和重对数律的精确渐近性。本文给出独立同分布序列部分和之和精确渐近性的一般形式，主要结果如下：

(1)

其中N为标准正态分布随机变量。

注：(1)当1/3≤p

(2)

φ(n)=(logn)α+1,则有

(3)

式中logx=ln(x∨e)

式(2)和式(3)分别是文献[6]中定理1和定理3在独立情形时的结论。

1 两个引理

在定理1的条件下有下面两个引理:

2 定理1的证明

命题1

证明：

命题2

证明：记

则由引理2知△n→0,n→∞,结合Toeplitz引理[7]有:

命题3 关于0<ε<1一致地有

证明：

命题4 关于0<ε<1一致地有

证明：由马尔可夫不等式和引理1，有

由命题1～4并结合三角不等式可知式(1)成立。

[1]ResnickSL.LimitLawsforRecordValues[J].StochasticProcessesandTheirApplications，1973，1(1):67-82.

[2]ArnoldBC，VillasenorJA.TheAsymptoticDistributionsofSumsofRecords[J].Extremes，1998，1(3):351-363.

[3] 江涛，林日其.I.I.D.随机变量部分和之和的极限定理[J].淮南工业学院学报，2002，22(2):73-75.

[4] 宇世航.同分布NA序列部分和之和的强大数定律[J].山东大学学报:理学版，2008，43(4):62-66.

[5] 兰冲锋,吴群英.I.I.D序列部分和之和的完全收敛性探讨[J].吉林大学学报: 理学版，2012,50(3):507-510.

[6] 邹广玉，吕阳阳.NA序列部分和之和的大数定律和重对数律的精确渐近性[J].吉林大学学报:理学版，2015,53(1):54-58.

[7] STOUT W F.Almost Sure Convergence[M].New York: Academic Press, 1995:120.

(责任编辑：张英健)

General Law of Precise Asymptotics for the Sum of Partial Sums of Independent and Identically Distributed Sequences

ZHOU Guangyu

(School of Science, Changchun Institute of Technology, Changchun Jilin 130012, China)

Applying the asymptotic properties for the sum of partial sums of independent and identically distributed sequences, the author obtained a general law of precise asymptotics for the sum of partial sums of independent and identically distributed sequences, which enrich the results of precise asymptotics for independent and identically distributed sequences.

independent and identically distributed sequence; sum of partial sums; precise asymptotics

10.16018/j.cnki.cn32-1650/n.201504004

2015-06-15

国家自然科学基金资助项目(11401190)；吉林省教育厅资助项目(120120113)；长春工程学院青年基金资助项目(320130019)

邹广玉(1982-)，男，吉林通化人，讲师，博士，主要研究方向为概率极限理论。

O211.4

A

1671-5322(2015)04-00015-02