基于对角稀疏拟牛顿技术的非单调曲线搜索的记忆梯度算法

刘丽敏, 吴玉敏

(中国石油大学胜利学院 基础科学学院,山东 东营 257000)

基于对角稀疏拟牛顿技术的非单调曲线搜索的记忆梯度算法

刘丽敏, 吴玉敏

(中国石油大学胜利学院 基础科学学院,山东 东营 257000)

基于对角稀疏拟牛顿技术,结合曲线搜索步长规则、Gu N.Z.非单调技术,建立一种新的求解无约束最优化问题的记忆梯度算法,同时,给出了算法的全局收敛性分析。数值例子表明:算法是有效的,适合求解大规模问题。

非线性规划;对角稀疏拟牛顿算法;非单调技术;曲线搜索;记忆梯度算法;收敛

1 技术手段

20世纪60年代末,Miele和Cantrell首先提出的记忆梯度法[1]可以有效利用前面迭代点的信息。2006年,时贞军[2]基于拟牛顿方程,通过限制Hk为对角稀疏正定矩阵,提出了对角稀疏拟牛顿算法,算法存储量降为O(n),使其利于求解大规模问题。根据目标函数f(x)的Taylor展开式,Wei Z X[3]给出了非拟牛顿方程,并且给出了Ak的两种取法:

(1)

(2)

其中,vk=2(fk-fk+1)+(gk+1+gk)Tsk。2012年,孙清滢[4]给出了另外一种新的取法:

(3)

同时,提出Hk如下修正形式:

设Hk为对角稀疏正定矩阵,令Hk+1=Hk+ΔHk,其中,ΔHk为对角矩阵。这时Hk+1为对角矩阵且要求近似满足非拟牛顿条件:

(4)

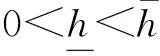
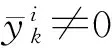
近年来,曲线搜索技术应用到优化算法中,使算法在曲线上搜索下一个迭代点,在确定步长的同时确定下降方向,得到了一些收敛效果好的算法[5]。非单调线搜索技术具有使算法快速收敛和便于求解全局最优解的优点,最近,Gu和Mo[6]提出了一种新的非单调线搜索技术,在新的非单调线搜索技术中改进了传统非单调技术中的参考值的选取。

本文在修正拟牛顿方程的基础上,结合了对角稀疏拟牛顿技术、记忆梯度算法的思想,用前一次迭代方向去修正-Hkgk得到算法的迭代方向,结合Gu N.Z.非单调技术和曲线搜索步长规则,建立求解无约束最优化问题的新的记忆梯度算法,并给出了算法的全局收敛性分析。给出数值例子验证算法的有效性,确实适合求解大规模问题。

2 算 法

基于稀疏对角拟牛顿技术的Gu N.Z.非单调曲线搜索的记忆梯度算法(NMDSMG):

步骤2令

(5)

步骤3令xk+1=xk+αkdk(αk),选取步长αk为{1,ω,ω2,…}中满足下式的最大者

(6)

其中,

(7)

其中,Hk由式(4)确定。

步骤4通过某种规则给出ηk∈[ηmin,ηmax],令

Dk+1=ηkDk+(1-ηk)f(xk+1).

(8)

令k:=k+1,转步骤1。

证明 由dk的定义和Hk的取法易证。

证明 由式(7)和Hk的构造知

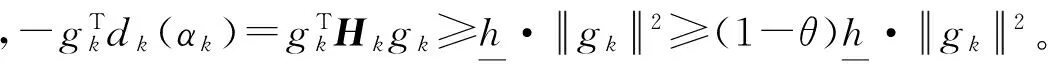
引理3 设{xk}是由算法NMDSMG产生的序列,则有

1)f(xk+1)≤Dk,∀k;

2)f(xk)≤Dk,∀k;

3){Dk}是单调不增序列。

证明 见文献[4]中引理3的证明。

3 全局收敛性

设算法NMDSMG产生的点列为{xk},如果存在某个k使得f(xk)=0,那么xk就是问题(p)的稳定点。下面假设算法中产生的点列{xk}为无穷点列,全局收敛结果如下:

定理1 假设目标函数f(x)在水平集L0={x∈Rn|f(x)≤f(x0)}上有下界,算法产生无穷点列{xk},如果目标函数f(x)的梯度f(x)在包含L0的某开凸集上一致连续,那么点列{xk}的任一极限点都是问题(p)的稳定点。

由式(6)和式(8)知

Dk+1=ηkDk+(1-ηk)f(xk+1)≤

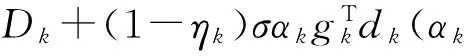
(9)

由ηmin<1、式(9)和引理2知

(10)

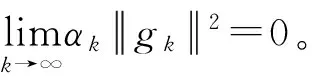
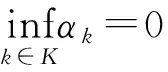
由引理3知

(11)

根据中值定理,可得

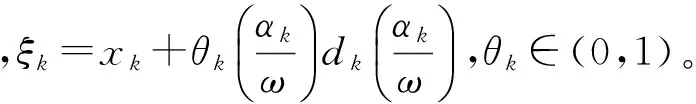
(12)

由Cauchy-Schwarz不等式、引理1、引理2及式(12)可得

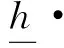
(13)

因为{xk}k∈K有界,g(x)连续,因而{gk}k∈K有界,设其界为M>0,则由式(13)可知

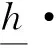
(14)

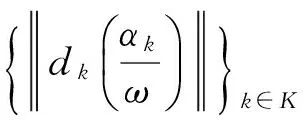
(15)

4 数值实验

从文献[5,7]中选择2个数值例子,利用Matlab7.0在电脑上编制程序对本文算法进行数值实验,同时与其单调算法进行比较。

当Ak取式(1)、式(2)、式(3)及Ak=0时,算法NMDSMG对应的算法为NMDSMG(1)、NMDSMG(2)、NMDSMG(3)及NMDSMG(0);当ηk≡0时,算法NMDSMG(1)、NMDSMG(2)、NMDSMG(3)及NMDSMG(0)分别对应其单调算法,记为MMG(1)、MMG(2)、MMG(3)及MMG(0)。当Bk≡In时,记为NGM;当ηk≡0时,算法NGM对应其单调算法,记为GM。当Bk用DFP公式修正时,算法记为DMMG;当Bk用BFGS公式修正时,算法记为BMMG;在算法DMMG、BMMG中取η≡0时,分别对应其单调算法,分别记为MDMMG、MBMM。

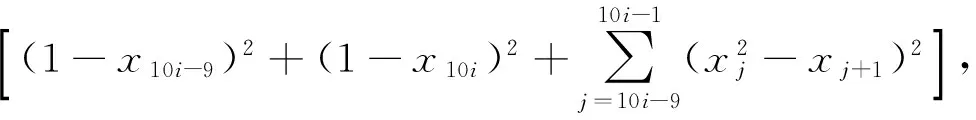
初始点x0=(-2,-2,…,-2)T,最优值。

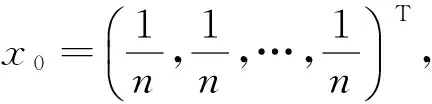
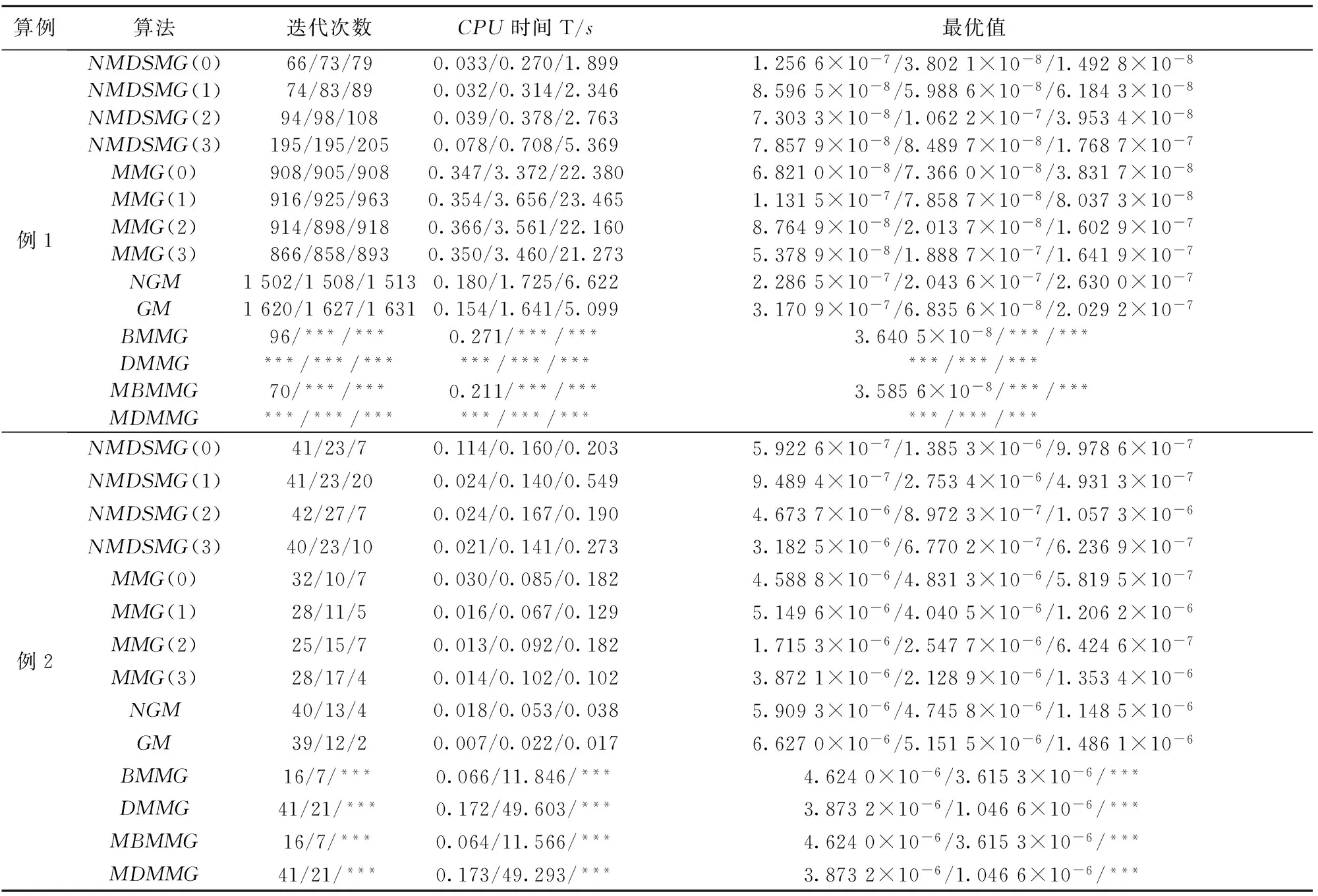
表1 例1、2的计算结果

5 结束语

本文在对角稀疏拟牛顿技术的基础上,结合了Gu和Mo非单调曲线搜索规则,建立了求解无约束最优化问题的新的记忆梯度算法,给出了算法的全局收敛性。数值例子表明算法是有效的,确实适合求解大规模问题。在传统算法中,Hk是用BFGS公式和DFP公式校正,而在新算法中,Hk是用公式(4)校正。新算法更适用于计算大规模问题,因为它的存储量小、计算量小,并且迭代时间短、迭代次数少,目标函数值更接近于最优值,而且所要解决问题的规模越大、维数越高,新算法优势就越明显。对有些数值例子来说,非单调算法的数值表现要优于单调算法。

[1] MIELE A,CANTRELL J W.Memory gradient method for the minimization of functions[J].Journal of Optimization Theory and Applications,1969,3(6):459- 470.

[2] 时贞军,孙国.无约束优化问题的对角稀疏拟牛顿法[J].系统科学与数学,2006,26(1):101-112.

[3] WEI Z X, LI G Y, QI L Q. New quasi-Newton methods for uncon- strained optimization problems[J].Applied Mathematics and Computation,2006,175(2):1156-1188.

[4] 孙清滢,徐琳琳,刘丽敏,等.基于稀疏对角拟牛顿方向的非单调超记忆梯度算法[J].工程数学学报,2012,29(3):375-385.

[5] SHI Z J,SHEN J.A new descent algorithm with curve search rule[J].Applied Mathematics and Computation,2005,161(3):753-768.

[6] GU N Z,MO J T.Incorporating nonmonotone strategies into the trust region method for unconstrained optimization[J].Computers and Mathematics with Applications,2008,55(9):2158-2172.

[7] TOUATI-AHMED D,STOREY C.Efficient hybrid conjugate gradient techniques[J].Journal of Optimization Theory and Applications,1990,64(2):379-397.

[责任编辑] 蓝若水

2015-06-06

刘丽敏(1987—),女,山东潍坊人,中国石油大学胜利学院基础科学学院助教,硕士,主要从事数学教学与研究。

10.3969/j.issn.1673-5935.2015.03.009

O224

A

1673-5935(2015)03- 0028- 04