基于联合时频滤波的多目标回波信号分离算法*

张 栋，冯存前，贺思三，罗亚宗，罗 骁

（空军工程大学防空反导学院，西安 710051）

基于联合时频滤波的多目标回波信号分离算法*

张 栋，冯存前，贺思三，罗亚宗，罗 骁

（空军工程大学防空反导学院，西安 710051）

针对弹道中段多目标回波信号分离的问题，提出了基于联合时频滤波的多目标信号分离算法。该算法先对多目标回波信号进行自相关处理和峰值提取，得到目标信号的周期，接着用该周期对回波信号的Gabor变换和PWVD变换结果进行分段，然后将各段时频图相乘，获得新的时频支撑域，最后用新的时频支撑域对回波信号进行时频滤波，克服了交叉项的干扰和时频聚集性不高的缺点，分离出了不同周期的目标信号。仿真结果证明了该方法的有效性和先进性。

微多普勒，联合时频滤波，信号分离

0 引言

微动特征反映了目标的电磁散射特性、几何结构特性和运动特性，近年来基于微动特性的弹道目标识别受到广泛关注［1-3］。Chen V.C.以理想点散射模型为基础，推导了振动、旋转、锥旋、摆动等基本微动的运动学模型［4-6］。张群根据旋转类微动信号为正弦调频信号的性质，引入图像处理中的Hough变换曲线检测方法，构建了基于TFD-Hough的参数化微动信号处理框架［7］。牛杰用经验模式分解算法对弹头回波数据进行了分解，得到了各散射中心对应的多普勒信息［8］。王璐等人提出了一种基于时频图的微动目标参数提取方法［9］。雷腾提出了一种基于时间——距离像的进动目标微动特征提取方法［10］。

但是在弹道中段，导弹周围将存在碎片以及诱饵甚至是多弹头等伴随飞行物，会形成威胁目标群，一个雷达波束将覆盖多个目标，从而导致多目标回波信号混叠在一起。现有中段目标特征提取算法都是针对单目标回波而言的，无法对群目标回波进行处理。本文提出了一种新的联合时频滤波算法，实现了中段多目标回波信号的分离。

1 模型分析

中段目标主要包括旋转和进动两种典型的微动模型，下面对这两种模型进行分析。

图1 旋转模型示意图

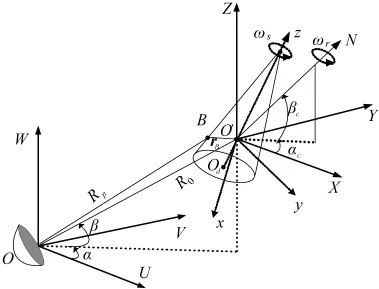
图2 进动示意图

1.1 旋转模型分析

分析弹道目标锥顶A，建立坐标系如图2所示，雷达位于O点处，O'N为旋转轴，散射中心A绕O'N以角速率ωr做旋转运动。OO'在雷达坐标系中的方位角和仰角分别为α和β，旋转轴O'N在参考坐标系（X，Y，Z）中的方位角和俯仰角分别为αr和βr，其中Tr为推导得到的t时刻目标的旋转矩阵，A在参考坐标系得初始位置为：

t时刻A点相对雷达的径向距离为：

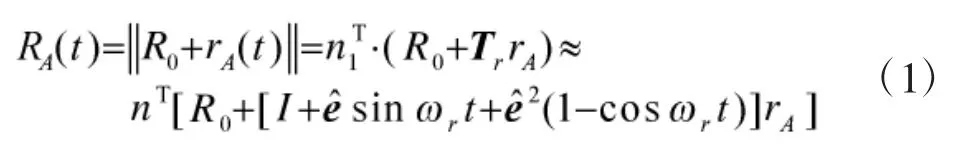
其中

LA、KA、φA均为与雷达视角，散射点位置及其在参考坐标系的视角有关的常数。

对于单频信号而言，忽略目标上各散射点散射强度随微动的变化时，单频信号回波为调频信号，对其进行时频分析即可得到目标微多普勒的变化规律。第i个散射点的微多普勒可表示为：

由式（2）和式（3）可见，理想散射中心作旋转微动时，其微多普勒呈正弦规律变化。

1.2 进动模型分析

同旋转模型下类似，建立坐标系如图2，分析弹道目标上的一进动散射点B，其中Tc和Ts为推导得到的t时刻目标的锥旋和自旋矩阵，则t时刻B点的微距离为：

对其进行时频分析即可得到目标微多普勒的变化规律。第i个散射点的微多普勒可表示为：

同理，由式（4）和式（5）可知，其微多普勒曲线不再符合简单的正弦调制规律而是几种正弦曲线的叠加。

2 时频分析方法

Gabor和PWVD是两种常用于非平稳信号分析的时频表示方法。下面对这两种方法进行介绍。

2.1 Gabor变换原理

Gabor展开先建立非平稳信号的时频函数，然后通过在时频面上采样划分，将时频面（t，f）转换成两个离散参数m和n的平面，最后在二维平面（m，n）上表示出非平稳信号［12］。信号x（t）的Gabor展开为：

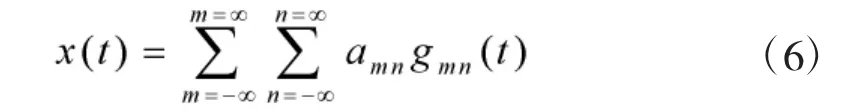
式中，gmn（t）称为基函数，表达式为：

式中：F为频率长度；T为时间长度；amn为Gabor系数，表达式为：

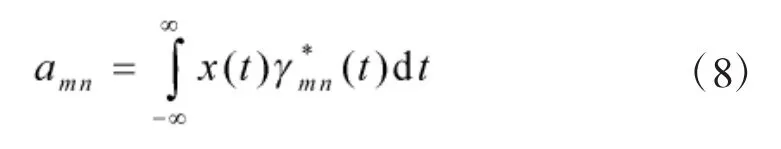
式中，γmn（t）是gmn（t）的对偶函数。

Gabor变换属于线性时频表示，因此，从根本上克服了交叉项问题，不存在交叉项干扰，但是时频分辨率低。

2.2PWVD原理

信号x（t）的WVD定义式为：

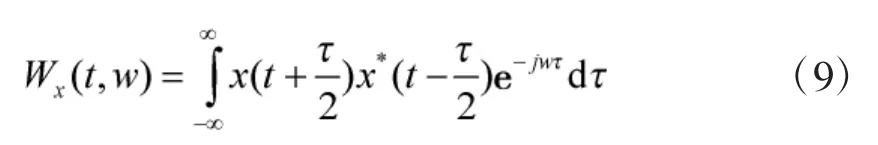
它表示的是信号的时频能量密度，令x（t）=x1（t）+ x2（t），得到：

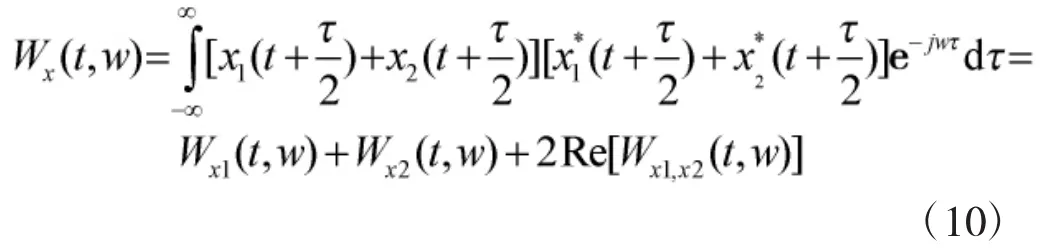
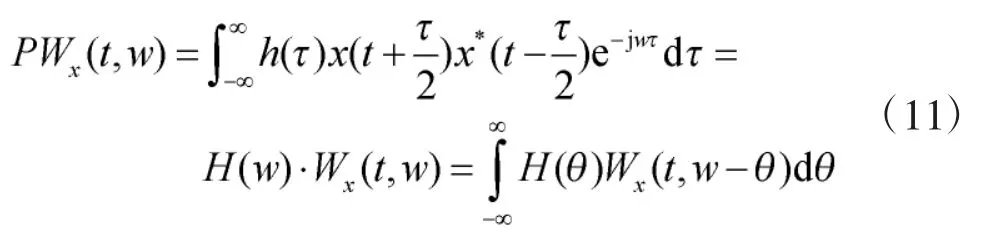
PWVD具有很好的时频聚集性，但是它不再服从线性叠加原理，存在非线性失真和严重的交叉项，而且信号分量越多，交叉项就越多，这是PWVD分布的一个重大缺点。

3 目标分离算法

由前面第1节的分析可知，中段不同的微动目标服从不同的运动规律，在时频图上有不同的分布形式。但是它们都是具有周期性，不同目标所对应的微动周期不一致。微动的周期性对应了回波变化的周期性，因此，首先可通过对回波信号的周期性分析估计出目标的个数及对应周期。该类算法已十分成熟，本文采用回波信号自相关以及峰值提取法求得目标个数以及对应的周期。

在估计出某一周期Tr后，对时频分析结果以Tr为单位划分为多个时间段：对周期为Tr的信号分量而言，在各时间段内其对应回波信号在时频面上所对应的强能量区域是一致的，而其他信号分量不具有此特性。因此，可通过对时频图上多个时间段进行分析，提取出具有相同周期Tr的信号分量在时频面上的支撑域，从而进一步根据支撑域对群目标信号进行时频滤波得到具有相同周期特性的信号，也就分离出了不同的目标信号。

由第2节分析可知，Gabor变换不存在交叉项干扰，但是时频分辨率低。PWVD具有很好的时频聚集性，但是存在非线性失真和严重的交叉项。这两种时频分析方法均有各自的优缺点，单独采用其中一种方法效果不理想，因此，本文采取两种方法相结合的手段。

综合以上分析，基于联合时频滤波的弹道中段多目标回波信号分离算法的具体步骤如下：

Step 1：假设雷达发射单载频信号，对回波信号进行自相关处理以及峰值提取，根据提取的结果确定目标数目和目标微动周期；

Step 2：对回波信号分别进行Gabor变换和PWVD变换，得到两种不同的时频分布图；

Step 3：根据提取的周期对两种时频分布图进行分段，对分段后的结果进行二值化处理，得到时频支撑域；

Step 4：将两种方法的各段时频支撑域进行点乘得到综合的时频支撑域；

Step 5：用新的时频支撑域对目标回波信号进行滤波，分离出想要的目标信号。

分段时所用的周期不同，就可以得到对应周期的目标回波信号，需要指出的是，上述方法所分离后的信号将具有相同的微动特性。对同一个目标上具有不同运动模式的散射中心而言，将辨识为两个目标。如对带尾翼的弹头而言，由于弹体具有旋转对称性弹体与尾翼的运动模式不同，分离后将弹体和弹翼所对应信号辨识为不同的目标。这对后续的特征提取是有利的。

流程图如图3所示。

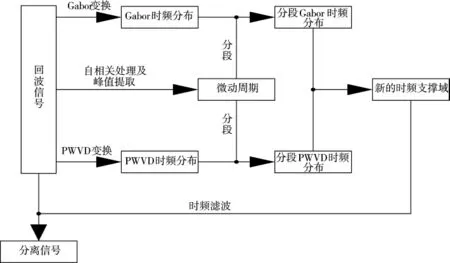
图3 算法流程图

4 仿真实验

信号仿真参数设置：单频脉冲信号雷达载频f=5 GHz，脉冲重复频率为2 KHz。参考坐标系原点O'到雷达的径向距离为1 000 m，假设存在两个旋转目标和一个进动目标。

旋转模型仿真参数设置：两个旋转点在参考坐标系中的初始坐标均为（0，0，1.5），单位为m。旋转角速度分别为ωr=2π rad/s和rad/s。旋转轴的方位角和俯仰角分别为60°和45°。

进动模型仿真参数设置：假设在本体坐标系（x，y，z）中进动点的坐标分别为（0.3，0.4，0.5），单位为m。本体坐标系（x，y，z）相对于参考坐标系（X，Y，Z）的初始欧拉角为（45°，30°，20°）。锥旋轴O'N在（X，Y，Z）中的方位角和高低角分别为60°和45°，自旋角速度ωs和锥旋角速度ωc分别为和。

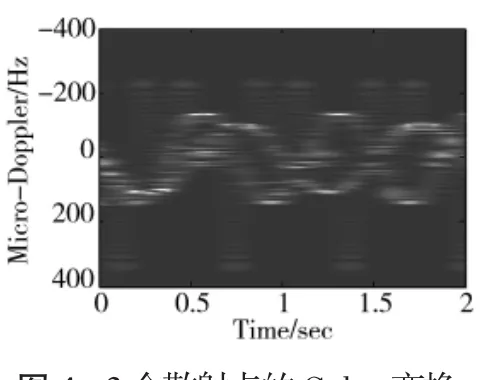
图4 3个散射点的Gabor变换

图5 3个散射点的PWVD变换

图4和图5分别为3个目标回波的Gabor变换和PWVD变换，3个目标信号交叠在一起。可以看出Gabor变换不存在交叉项但是时频聚集性不高，PWVD变换时频聚集性高但是存在交叉项。

经过信号自相关处理以及峰值提取，可知信号中含有3个目标，而且3个目标周期分别为0.75 s、0.675 s、1 s。

图6～图8分别为散射点1的Gabor支撑域、PWVD支撑域和联合支撑域，可以看出单纯由Gabor变换经分段融合处理得到的时频支撑域聚集性不好，单纯由PWVD变换经分段融合处理得到的时频支撑域包括交叉项的影响。而经过两种方法综合处理得到的联合支撑域拥有更好的聚集性，而且降低了交叉项的干扰。

图6 散射点1的Gabor支撑域

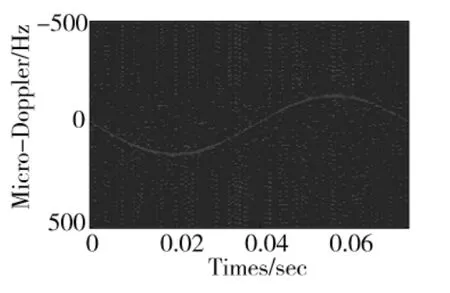
图7 散射点1的PWVD支撑域

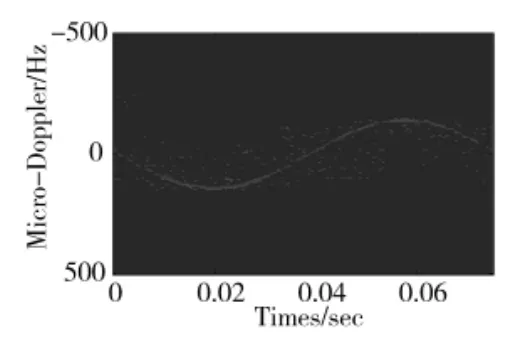
图8 散射点1的联合支撑域

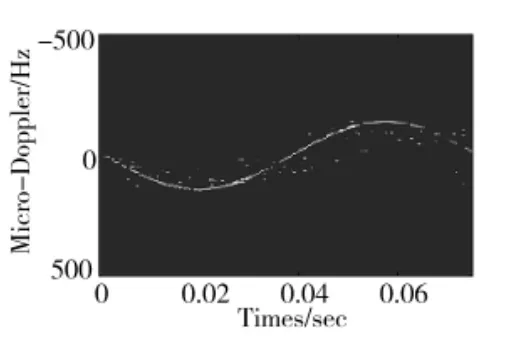
图9 分离得到的散射点1信号

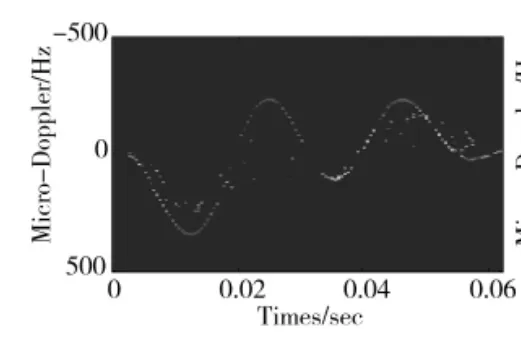
图10 分离得到的散射点2信号

图11 分离得到的散射点3信号

图9～图11分别为经过分离得到的3个散射中心回波信号在时频域上的表示。可以看出该方法可以很好地分离不同周期的目标信号。而且分离得到的目标信号拥有很高的时频聚集性，不存在交叉项的干扰。

5 结束语

弹道目标微动特征提取及其应用已成为当前研究的一个热点，但是大多数研究均未考虑到中段的多目标问题。本文针对弹道中段多目标回波信号分离的问题，提出了基于联合时频滤波的多目标信号分离算法，克服了单一时频滤波存在的时频聚集性不高以及交叉项干扰的缺点，分离出了不同周期的目标回波信号，为下一步的微动特征提取打下了基础。

［1］Chen V C，Li F Y，Ho S S，et al.Micro-Doppler Effect in Radar Phenomenon Model and Simulation Study［J］.IEEE Trans on AES，2006，42（1）：2-21.

［2］Luo Y，Chi L，Zhang Q，et al.A Novel Method for Extraction of Micro-Doppler Signal［C］//IEEE 2007 International Symposium on Microwave Antenna Propagation and EMC Technologies for Wireless Commu Nications.Hangzhou：IEEE Press，2007：1458-1462.

［3］Chen V C.Spatial and Temporal Independent Component Analysis of Micro-Doppler Features［C］//IEEE International Radar Conference Arlington.Virginia：IEEE press，2005：348-353.

［4］Chen V C.Doppler Signatures of Radar Backscattering from Objects with Micro-motions［J］.IET Signal Processing，2008，2（3）：291-300.

［5］Chen V C，Li F.Analysis of Micro-doppler Signatures［J］. IEEE Proc Radar Sonar Navig，2003，150（4）：271-276.

［6］Chen V C.Analysis of Radar Micro-Doppler Signature with Time-frequency Transform ［C］//Proceedings of IEEE Workshop on Statistical Signal and Array Processing.IEEE press，2000：463-466.

［7］张群，罗斌凤，管桦，等.基于微Doppler提取的具有旋转部件雷达目标成像［J］.自然科学进展，2007，17（10）：1410-1417.

［8］牛杰，刘永祥，秦玉亮，等.一种基于经验模态分解的锥体目标微动特征提取方法［J］.电子学报，2011，39（7）：1712-1715.

［9］王璐，刘宏伟.基于时频图的微动目标运动参数提取和特征识别的方法［J］.电子与信息学报，2010，32（8）：1812-1817.

［10］雷腾，刘进忙，余付平，等.基于时间-距离像的弹道目标进动特征提取新方法［J］.信号处理，2012，28（1）：73-79.

Multi Targets Echo Signal Separation Algorithm Based on Joint Time-ferquency Filtering

ZHANG Dong，FENG Cun-qian，HE Si-san，LUO Ya-zong，LUO Xiao
（Air and Missile Defense College，Air Force Engineering University，Xi’an 710051，China）

In view of the problem of multi targets echo signal separation in the ballistic midcourse，the separation algorithm is put forward.Firstly，the signal period is got by the autocorrelation and peak extraction to the multi targets enho signal.Then using the period to cut the signal's Gabor and PWVD transform results into segments.Then the new time-frequency support region is got by the multiplication to the segments.Lastly，the differnet signals can be separated by filtering to the echo signal though the new time-frequency support domain.It overcomes the interference of the cross terms and the shortcoming of low time-frequency concentration.Simulation results validate the effectiveness and advance of the proposed algorithm.

micro-doppler，joint time-frequency filtering，signal separation

TN957

A

1002-0640（2015）07-0012-04

2014-04-05

2014-07-20

国家自然科学基金资助项目（61372166）

张 栋（1990- ），男，河北辛集人，硕士。研究方向：目标微多普勒信息提取研究。