一类二阶四点p-Laplacian边值问题的3个正解

吴红萍，周韶林

(西北师范大学数学与统计学院，甘肃兰州730070)

一类二阶四点p-Laplacian边值问题的3个正解

吴红萍，周韶林

(西北师范大学数学与统计学院，甘肃兰州730070)

利用不动点定理，讨论二阶四点p-Laplacian非线性边值问题

其中:α，β＞0，0＜ξ＜η＜1．得到了3个正解存在的充分条件，并给出了1个实例.

多点边值问题;p-Laplacian算子;正解

考察二阶四点p-Laplacian非线性边值问题

其中:φp(s)=|s|p-2s，p＞1，α，β＞0，0＜ξ＜η＜1．f:［0，1］×［0，∞］×ℝ→［0，∞］连续.

过去的二十多年里，多点边值问题的研究受到极大的关注并取得了许多成果［1-7］.这些研究主要集中于以下边值条件:

其中:α，β＞0，0＜ξ＜η＜1．当α，β≠1，ξ=0，η=1，式(2)表示Dirichlet边值条件，式(3)和(4)表示混合边值条件，式(5)表示Nuemann边值条件.

对于带以下边界条件的Sturm-Liouville二阶边值问题

其中:α，γ，β，δ＞0且αγ+αδ+βγ＞0，也取得了许多正解存在结果［8-9］.然而，现有的文献考虑以下四点边值条件的很少，

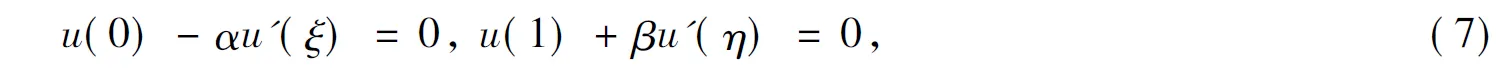
其中:0＜ξ＜η＜1．

Lian和Ge［10］讨论了以下类似于Sturm-Liouville型的二阶四点边值问题

通过使用锥上的不动点定理，获得了以上边值问题1个正解和2个正解的存在性结果.

受上述文献的启发，本文进一步讨论二阶四点p-Laplacian边值问题(1)，通过使用一个新的不动点定理，获得了该问题3个正解存在的新结果，尚无人涉及.

以下总假定:

1 预备与引理

引理1［10］假设e∈L1［0，1］，e(t)≥0，在［0，1］的子区间上e(t)≠0，则边值问题

有唯一一个解:u∈C［0，1］∩C1(0，1)，并且这个解可表示为

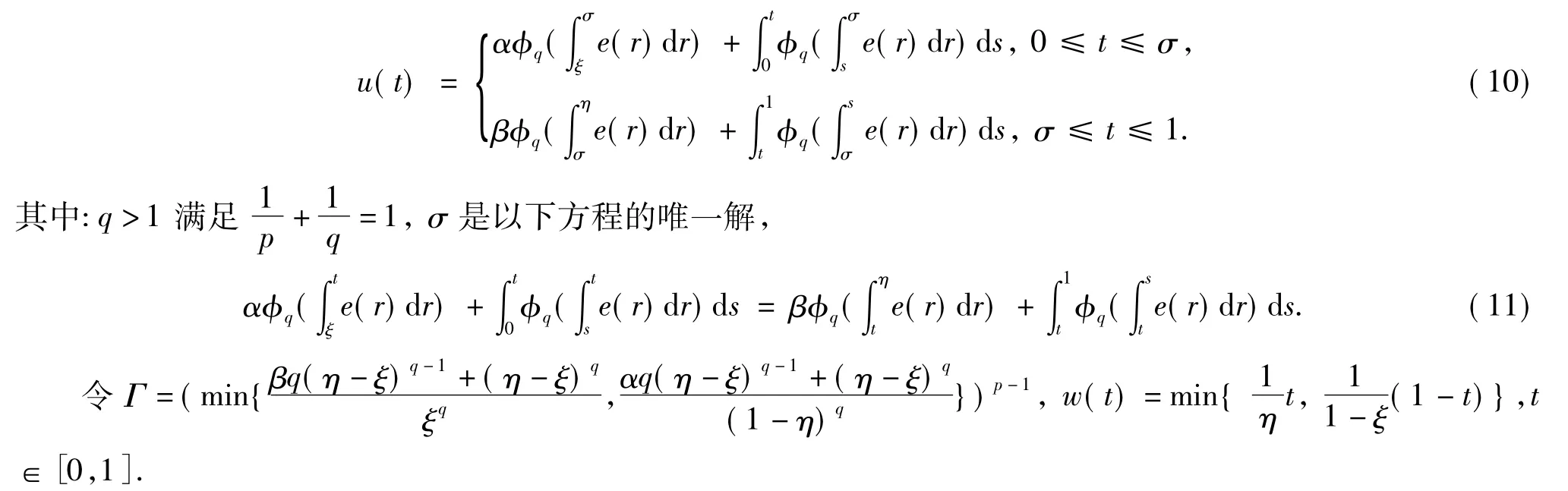
引理2［10］设e∈C［0，1］满足引理1的条件，进一步假定maxt∈［0，ξ］∪［η，1］e(t)≤Γmint∈［ξ，η］e(t)，则边值问题(9)的解u必然是非负凸的，且在［0，ξ］上递增，［η，1］上递减，满足u(t)≥w(t)‖u‖，t∈［0，1］．

考虑Banach空间E=C1［0，1］，定义其范数为‖u‖=max{max0≤t≤1|u(t)|，max0≤t≤1|u'(t)|}．在E中定义锥P．

P={u∈E，u(t)≥0，u(t)是凸的且在［0，ξ］上递增，在［η，1］上递减，t∈［0，1］}．

注记如果u∈P∩C1(0，1)，必然存在σ∈［ξ，η］使得u'(σ)=0，这对于u(t)的正解存在性非常重要，与此同时当u∈P，t∈［0，1］时，u(t)≥w(t)‖u‖成立．

引理3［10］T:P→P全连续.

假设φ，ω:P→［0，∞)是2个非负连续凸泛函，满足

其中:M＞0是一常数，令

结合式(12)和(13)知Ω是P中的1个有界非空开子集．

定义1设r＞b＞0，L＞0，φ，ω:P→［0，∞)是2个非负连续凸泛函，满足式(12)和(13)，ψ是P上的非负连续凹泛函，定义以下有界凸集

引理4［11］设E是一个Banach空间，P⊂E是一个锥，r2≥d＞b＞r1＞0，L2≥L1＞0，φ，ω是P上的2个非负连续凸泛函，满足式(12)和(13)，ψ是P上的非负连续凹泛函，使得当x∈¯P(φ，r2;ω，L2)时，ψ(x)≤φ(x)，T:¯P(φ，r2;ω，L2)→¯P(φ，r2;ω，L2)是全连续算子．假设以下条件满足:

(A1){x∈¯P(φ，d;ω，L2;ψ，b)|ψ(x)＞b}≠∅，ψ(Tx)＞b，x∈¯P(φ，d;ω，L2;ψ，b).

(A2)φ(Tx)＜r1，ω(Tx)＜L1，∀x∈¯P(φ，r1，ω，L1)．

(A3)ψ(Tx)＞b，∀x∈¯P(φ，r2;ω，L2;ψ，b)时φ(Tx)＞d．

则T至少有3个不动点x1，x2，x3∈¯P(φ，r2;ω，L2)，且x1∈¯P(φ，r1;ω，L1)，x2∈{¯P(φ，r2;ω，L2;ψ，b)|ψ(x)＞b}，x3∈¯P(φ，r2;ω，L2)(¯P(φ，r2;ω，L2;ψ，b)∪¯P(φ，r1;ω，L1))．

2 主要结果

注记w*＜1．

定义函数

则φ，ω，ψ:P→［0，∞)均为非负连续函数，取‖u‖=max{φ(u)，ω(u)}，则式(12)，(13)成立;φ(u)，ω(u)是凸的，ψ是凹的且有ψ(u)≤φ(u)，∀u∈P．

则边值问题(1)至少有3个正解u1，u2，u3，满足max0≤t≤1u1(t)＜r1，max0≤t≤1|u'1(t)|＜L1，b＜minu2(t)＜maxt∈［0，1］u2(t)≤r2，max0≤t≤1|u'(t)|≤L2，mint∈u(t)＜b，maxu(t)≤，max0≤t≤1|u3(t)|≤L2．

证明以下证明引理4的所有条件均成立．

首先，如果u∈P¯(φ，r2;ω，L2)，则φ(u)≤r2，ω(u)≤L2，(B3)隐含f(t，u(t)，u'(t))≤φp(mr2)．因此

∀u∈P，有Tu∈P，由于Tu在［0，1］上是凸的，且maxt∈［0，1］|Tu'(t)|=max{|(Tu)'(0)|，|(Tu)'(1)|}．故

其次，同样的方法，如果u∈P¯(φ，r1;ω，L1)，条件(B1)满足，即f(t，u，v)＜min{φp(mr1，φp(L1)}，0≤t≤1．由此可得T:P¯(φ，r1;ω，L1)→P¯(φ，r1;ω，L1)，即引理4中的(A2)满足．

最后，证明引理4的条件(A3)也是满足的．设u∈P¯(φ，ω，L;ψ，b)，φ(Tx)＞则依据ψ的定义2及Tu∈P的事实，我们有

故引理4的条件(A3)也满足.

运用引理4，边值问题(1)至少存在3个正解，使得u1∈(φ，r1;ω，L1)，u2∈{P¯(φ，r2;ω，L2;ψ，b)| ψ(u)＞b}，u∈P¯(φ，r;ω，L)(P¯(φ，r;ω，L;ψ，b)∪P¯(φ，r;ω，L))．由于u满足φ(u)≤ψ(u)，故u(t)＜3

3 举例

以下给出实例来验证我们的结果.考虑二阶四点边值问题

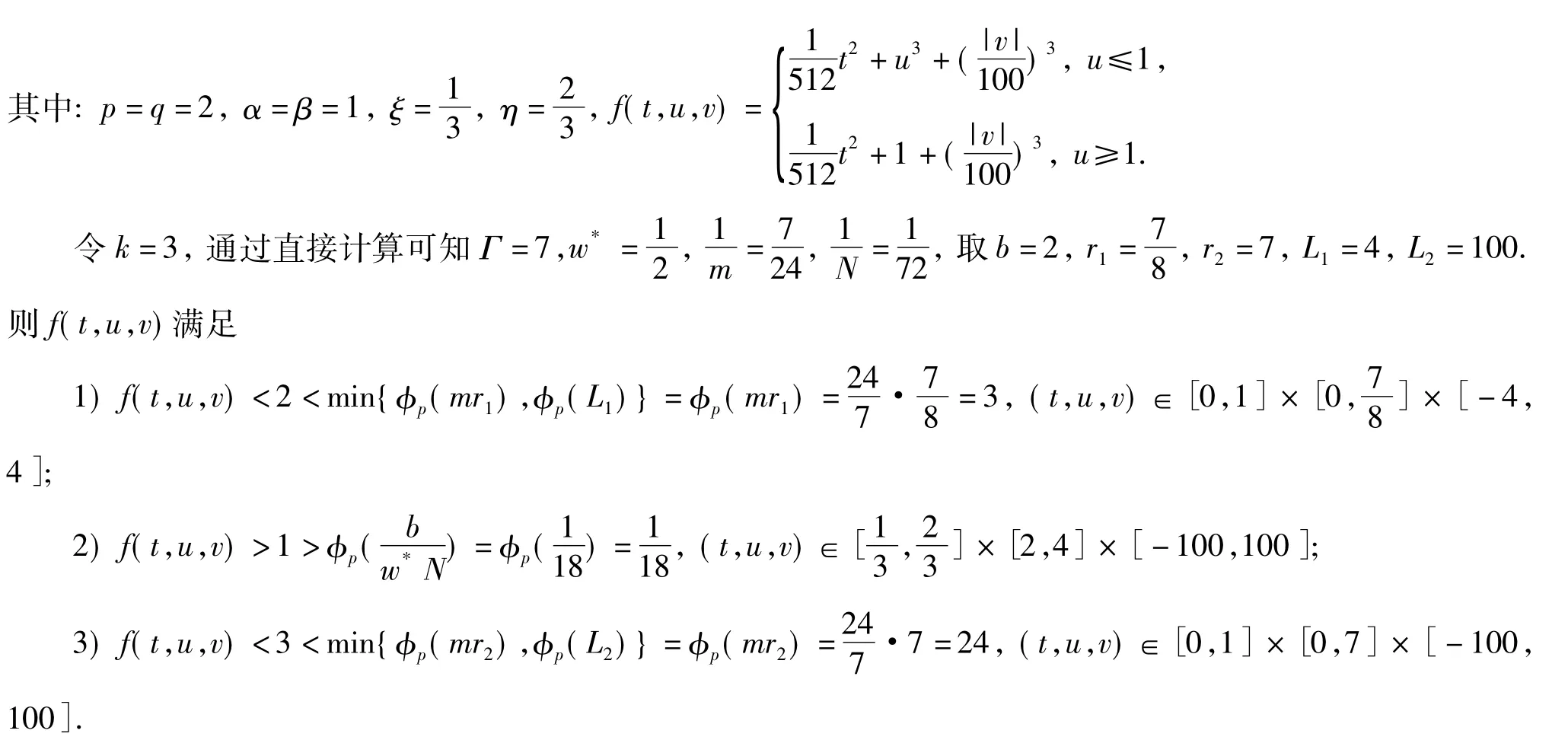
故定理1的全部条件满足，因此边值问题(14)至少存在3个正解u，u，u，且有mau(t)≤，

1231|u1'(t)|≤4，2＜2(t)＜ma(t)≤7，ma|u2'(t)|≤100，mau3(t)≤4，|u3'(t)|≤100．

［1］Bai Chuanzhi，Fang Jinxuan.Existence of multiple positive solutions for nonlinear m-point boundary value problems［J］.Appl Math Copmut，2003，140:297-305.

［2］Bai Zhanbing，Ge Weigao，Wang Yifu.Multiplicity results for some second-order four-point boundary value problems［J］.Nonl Anal，2005，60:491-500.

［3］Gupta C P，Trofimchuck S.A prior estimates for the existence of a solutions for a multi-point boundary value problem［J］.J Inequal Appl，2000，5:351-365.

［4］Liu Bing.Positive solutions of a nonlinear four-point boundary value problem［J］.Appl Math Copmut，2004，155:179-203.

［5］Su Hua，Wei Zhongli，Wang Baohe.The existence of positive solutions for a nonlinear four-point sigular boundary value problem with a p-Laplacian operator［J］.Nonl Anal，2007，66:2204-2217.

［6］Wong P J，Agarwal R P.Generalized multi-point conjugate engenvalue problem［J］.Math Comput Modelling，2000，32:733-745.

［7］Wang Youyu，Hou Chengmin.Existence of multiple positive solutions for one-dimensional p-Laplacian［J］.J Math Anal Appl，2006，315:144-153.

［8］Erbe L H，Wang Haiyan.On the existence of positive solutions of ordinary differential equations［J］.Proc Amer Soc，1994，120:743-748.

［9］Ge Weigao，Ren Jingli.New existence of positive solutions for Sturm-Liouville boundary value problems［J］.Appl Math Copmut，2004，148:631-644.

［10］Lian Hairong，Ge Weigao.Positive solutions for a four-point boundary value problem with the p-Laplacian［J］.Nonl Anal，2008，68:3493-3503.

［11］Bai Zhanbing，Ge Weigao.Existence of three positive solutions for some second-order boundary value problems［J］.J Comp Math Appl，2004，48:699-707.

Three Positive Solutions for a Second-order Four-point Boundary Value Problem with the p-Laplacian

WU Hong-ping，ZHOU Shao-lin
(College of Mathematics and Statistics，Northwest Normal University，Lanzhou 730070，China)

multi-point boundary value problem;p-Laplacian operator;positive solution

O175.8

A

(责任编辑 李春梅)

1004-8820(2015)02-0079-05

10.13951/j.cnki.37-1213/n.2015.02.001

2014-09-22

国家自然科学基金资助项目(11261053);甘肃省自然科学基金资助项目(1308RJZA125).

吴红萍(1970-)，女，甘肃庆阳人，副教授，硕士，主要研究方向:常微分方程边值问题.