V-BLAST系统的低复杂度改进裁剪QRD-M算法

王新忠，杨昕欣，李连合

(1.北京航空航天大学 电子信息工程学院，北京 100191；2.河南财经学校，河南 郑州 450012)

V-BLAST系统的低复杂度改进裁剪QRD-M算法

王新忠1，杨昕欣1，李连合2

(1.北京航空航天大学 电子信息工程学院，北京 100191；2.河南财经学校，河南 郑州 450012)

V-BLAST系统中，信号的检测是关键环节，传统的算法难以同时保证较好的系统性能和较低的复杂度。提出一种低复杂度改进的QRD-M算法，算法基于QRD-M树搜索原理，路径扩展仅扩展候选集中的点，同时在每层更新SIC结果并用其度量作为自适应搜索半径，采用SE搜索策略在每层搜索幸存路径以避免不必要节点的访问与排序。性能和复杂度分析表明，所提算法在基本不损失性能的条件下，能有效降低V-BLAST系统的检测复杂度，更易于实现。

V-BLAST；QRD-M；搜索半径限制；SE搜索策略

的t值可以更好地在算法性能与复杂度之间做折中。仿真结果表明，所提算法在较小性能损失的情况下复杂度明显减少。

1 V-BLAST系统模型

典型的未编码V-BLAST系统如图1所示，假设系统发射天线数为Nt，接收天线数为Nr(Nr≥Nt)。

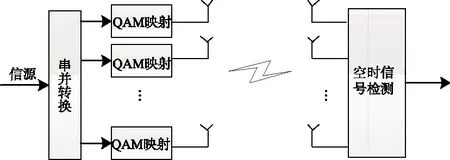
图1 V-BLAST系统框图

考虑一个时隙的离散复基带模型，则接收向量为

rc=Hcsc+Nc

(1)

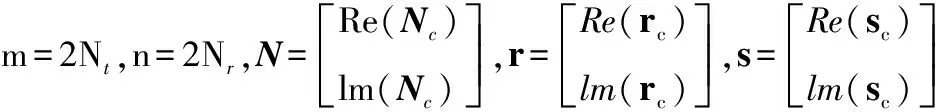
r=Hs+N

(2)

2 相关的V-BLAST系统检测算法

2.1 ML及串行干扰消除(SIC)算法

V-BLAST信号的检测算法就是采用某种准则利用接收信号r和信道矩阵H对发射信号s进行估计。发送信号s的ML估计为

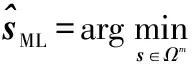
(3)

干扰消除算法(SIC)的实质是利用多天线分集增益提高了检测性能，SIC算法在检测时，将已检测并判决的层的信号从待检测信号中消除，从而消除已检测层信号的干扰。将信道矩阵直接进行QR分解可以得到ZF-QR-SIC算法。这里H=QR，其中n×m维矩阵Q满足QTQ=Im，m×m维的矩阵R为上三角矩阵。式两边同乘矩阵QT可得

y=QTr=Rs+v

(4)

式中：v=QTN为新的噪声向量。所以ZF-QR-SIC算法可以描述为

(5)

式中：Q[·]表示量化到最近的星座点操作。

SIC算法受检测顺序和误差传播等因素的影响，性能与ML检测的性能仍有较大差距。

2.2 传统的QRD-M树搜索检测算法

ML检测等价为

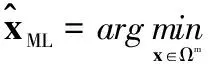
(6)

于是可以将ML检测问题描述为对一个加权树的最小路径搜索问题。完整的树模型如图2所示。

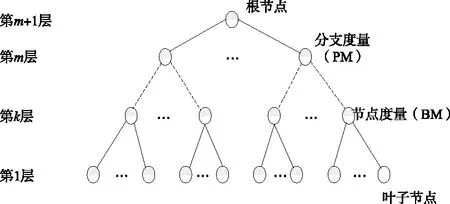
图2 V-BLAST信号检测的完整树模型

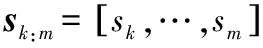
(7)

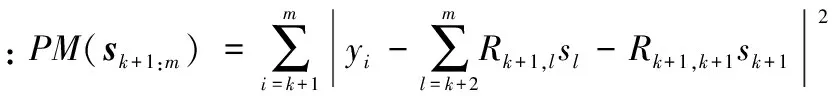
所以

(8)

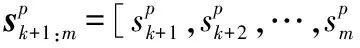
3 本文提出的低复杂度算法

常规的QRD-M算法的M值是固定的，M值影响着算法复杂度和性能。根据文献[5]建议，M取值需要不小于调制阶数，以获得接近ML的检测性能，此时算法具有较高的复杂度。QRD-M算法树扩展后候选路径数为cM。算法的主要复杂度就在于这cM个候选路径度量的计算和排序操作。所以降低复杂度可以从3方面出发：1)减少M，即在上一层保留较少的幸存路径；2)减少c；3)选择恰当的访问候选路径，以避免路径度量排序操作。

文献[5-6]两种算法分别从减少M和减少c两个方面降低算法复杂度，这里分别称为SIC-SQRDM，NP-SQRDM。SIC-SQRDM算法利用SIC的解计算每层的门限值，然后利用此门限值控制该层的幸存路径数。NP-SQRDM算法通过扩展在QRD算法解的周围固定的候选集而不是整个星座集来减少计算量。但是每种算法都有局限性，NP-SQRDM在高信噪比时性能有损失，SIC-SQRDM算法的复杂度在低信噪比时依然偏高。另外，二者都需对候选的节点度量进行排序操作。文献[7]将二者结合，但依然需要访问多余节点和排序操作。

SE策略[9-10]因较高的搜索效率被广泛应用在SD算法的检测中。同样，SE策略也可以用在QRD-M算法中。SE策略对于每个父节点首先展开其“最好”的子节点，即估计的中心点，也是路径度量增量最小的子节点，称为第一个子节点(First Child，FC)，然后按照之字形(Zig-Zag)方式沿星座图搜索其相邻节点(Next Child，NC)。不用排序就可以得到同一个父节点下各子节点度量(PM)的大小顺序。采用SE搜索策略仅需扩展少量需要保留的路径，其余路径不需扩展，避免了多余路径的度量与排序计算大大减少了算法复杂度。关于SE搜索策略的原理可以参考相应文献[9-10]，这里不做详细描述。

本文提出一种低复杂度算法，算法的模型为实数模型，算法有3个关键点：

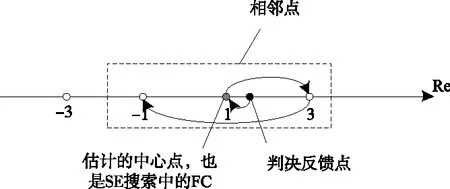
图3 中心点和两个邻节点构成的候选集

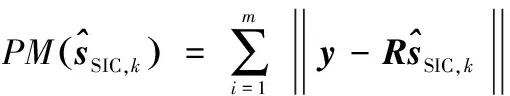
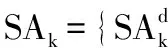
算法的具体描述如下：

1)采用MMSE-SQRD方式对信道矩阵进行QR分解。并初始化参数：R，y，M，t，sm+1:m=Φ，PM(sm+1:m)=0，k=m。

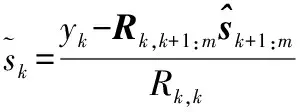
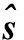
3)k=k-1，重复2)，直到k=1，检测完所有层之后，具有最小度量PM的路径即为最终检测结果。

该算法在每层保留路径数M基础上，使用了对信噪比敏感的SIC检测结果限制分支度量，并限制搜索范围为估计中心点周围的候选集，采用SE搜索策略使得算法在信噪比较高时可以有效减少路径扩展数，避免多余路径的访问与排序，降低了复杂度。

4 算法的复杂度及性能分析

通过蒙特卡罗仿真对算法性能及复杂度进行评估。系统为4×4 V-BLAST(即m=8)系统，收发两端天线互不相关，调制方式为16QAM，星座图映射方案采用3GPP LTE的调制映射方案。信道为平坦瑞利衰落，且接收端完全已知。算法性能以误码率(BER)作为衡量标准。信噪比SNR=E(‖Hs‖2)/E(‖N‖2)。

4.1 复杂度分析

本文中所有算法都是基于QR分解的，SIC算法的复杂度相对于QRD-M算法较小，故分析时不考虑二者的复杂度。本文用检测每一发送向量所需访问的节点数BN表示算法的复杂度。

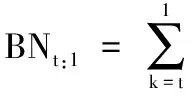
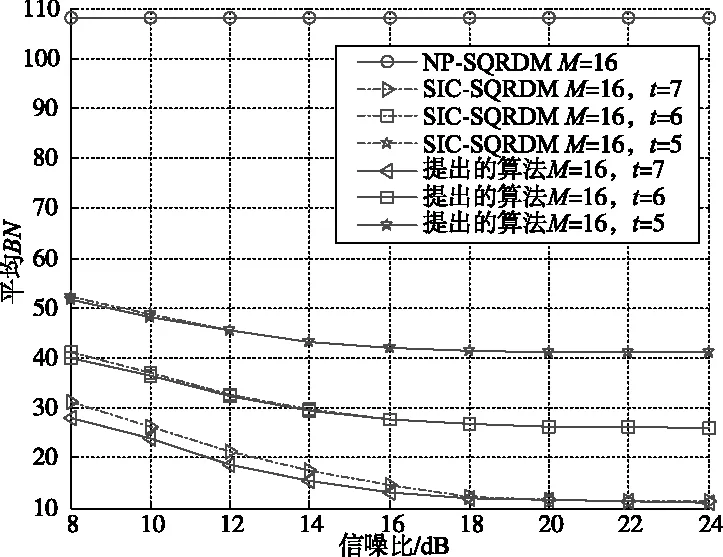
图4 不同算法访问点数

传统SQRD-M算法树搜索时访问的节点数是固定的，当M=16时，访问节点数为BN=4+4×4+16×4×6=404，如果采用SE搜索策略则BN=4+16×7=116。观察图4，在t=7时，所提算法访问节点数BN在M取不同数值时均小于SQRD-M算法的访问点数，另外所提算法的BN随着信噪比(SNR)的增加呈下降趋势，并最终在11附近。取M=16，在SNR=20dB时，所提算法的平均BN不到12，访问节点数大大减少。低信噪比时所提算法比SIC-SQRDM的BN要少约10%。在t取不同值时，算法将访问不同数量的节点，t越大，访问的节点越少，算法复杂度越低。

4.2 性能分析

图5为不同算法性能对比曲线。这里所提算法中的t=m-1=7，即仅在第m层采用SQRD-M算法，在后续各层采用限制半径的SQRD-M算法。由图可以看出，在同为M=16的条件下，所提算法与SIC-QRDM性能较为接近，与传统SQRD-M算法性能相比有一些性能损失，但损失很小，在M=16，BER=10-4时性能约差0.4dB。随着t的减小，即采用所提算法树搜索半径限制开始越晚，算法性能越好，在t=5时，所提算法与SQRD-M算法性能基本重合。

图5 16QAM 4×4 模式下算法性能

对比仿真结果，可以得出结论，在t值选择恰当时，所提算法能在几乎不降低性能的前提下，有效降低算法复杂度。而M的取值越大，算法性能越好，复杂度降低越明显。

5 小结

V-BLAST系统中，信号的检测是关键，传统的算法难以在性能和复杂度两方面进行有效的折中。本文提出的低复杂度改进算法采用将路径扩展限制在估计的中心点附近，同时用SIC的解限制扩展半径，结合SE搜索策略避免访问不必要的节点和排序操作，同时引入变量t以在复杂度和性能做折中。该算法在预处理阶段采用MMSE排序的QR分解。性能和复杂度分析表明，所提算法能在性能几乎不损失的条件下有效减少了访问节点数，避免了排序运算，降低了算法的复杂度。

[1]MURUGANAD,GAMALHE,DAMENMO,etal.Aunifiedframeworkfortreesearchdecoding:rediscoveringthesequentialdecoder[J].IEEETrans.InformationTheory, 2006,52(3):933-953.

[2]DAIYongmei,SUNSumei,LEIZhongding.AcomparativestudyofQRD-MdetectionandspheredecodingforMIMO-OFDMsystems[C]//Proc.IEEE16thInternationalSymposiumonPersonal,IndoorandMobileRadioCommunications(PIMRC2005).Berlin:IEEEPress,2005:186-190.

[3]熊春林,刘伟,王德刚,等.VBLAST系统中的裁减QRD-M树搜索检测算法[J].系统仿真学报, 2009,21(11):3378-3380.

[4]MAOX,CHENGY,XIANGH.PartialnoisevalueaidedreducedK-Bestspheredecoding[C]//Proc.IEEE78thVehicularTechnologyConference(VTCFall).LasVegas,NV:IEEEPress,2013:1-5.

[5]JEON K, KIM H, PARK H. An efficient QRD-M algorithm using partial decision feedback detection[C]//Proc. 40th Asilomar Conference on Signals, Systems and Computers (ACSSC ′)06). Pacific Grove, CA: IEEE Press,2006:1658-1661.

[6]KIM B, CHOI K. A very low complexity QRD-M algorithm based on limited tree search for MIMO systems[C]//Proc. Vehicular Technology Conference(VTC Spring 2008). Singapore: IEEE Press, 2008:1246-1250.

[7]XIN Xue, LI Xiaohui, HEI Yongqiang, et al. A modified QRD-M algorithm based on layer branch pruning for MIMO systems[C]//Proc. 24th IEEE International Conference on Advanced Information Networking and Application(AINA).Perth, WA: IEEE Press,2010:461-464.

[8]吴军，吴云龙，黄雅兰. 基于排序QR分解的VBLAST解码算法研究[J].电视技术，2014，38(7):149-152.

[9]DAMEN M O, GAMAL E, CAIRE G. On maximum-likelihood detection and the search for the closest lattice point[J].IEEE Trans. Information Theory,2003,49(10):2389-2402.

[10]GUO Z, NILSSON P. Algorithm and implementation of the K-best sphere decoding for MIMO detection[J].IEEE Journal on Selected Areas in Communications,2006,24(3):491-503.

王新忠(1989— )，硕士生，主研无线通信技术、LTE；

杨昕欣(1974— )，硕士生导师，主研通信信号处理、嵌入式系统、智能监控等；

李连合(1974— )，讲师，主研通信信号处理、机械电子。

责任编辑：薛 京

Modified QRD-M Algorithm with Low Complexity in V-BLAST System

WANG Xinzhong1, YANG Xinxin1，LI Lianhe2

(1.SchoolofElectronicandInformationEngineering,BeihangUniversity,Beijing100191,China; 2.HenanFinanceandEconomicsSchool,Zhengzhou450012,China)

Detection is the key to V-BLAST system. Traditional algorithm could not achieve high performance with low complexity. In the paper, a modified low complexity QRD-M algorithm is proposed. The algorithm reduce the complexity of tree searching by restricting the candidates to a set consists of QRD-based detection symbol and its neighboring symbols and branches trimming with adaptive search radius set by SIC result. SE searching strategy is also used to avoid visiting unnecessary branches and ordering operation. Performance and complexity analysis show that the proposed algorithm can reduce the complexity of the V-BLAST detection system without large loss of performance and could be implemented easily.

V-BLAST; QRD-M; search radius limit; SE search strategy

TN911.3

A

10.16280/j.videoe.2015.05.024

国家自然科学基金项目(61371077)

2014-08-27

【本文献信息】王新忠，杨昕欣，李连合.V-BLAST系统的低复杂度改进裁剪QRD-M算法[J].电视技术,2015，39(5).

无线通信中多天线技术(MIMO)的引入极大地提高了系统的吞吐量，而其中贝尔实验室提出的分层传输结构(V-BLAST)因简单有效而被广泛使用，也已成为3GPP的标准之一。V-BLAST系统中，检测是关键环节。在对该系统检测算法的研究主要体现在算法性能与复杂度两个方面。研究表明，误符号率最优的检测算法为最大似然(ML)算法[1]，但是因算法复杂度过高而在实际系统中难以实现。线性算法有迫零(ZF)和最小均方误差(MMSE)，复杂度低但性能较差。干扰消除算法(SIC)性能虽比线性算法好，但与ML算法有较大差距。球形译码算法(SD)能在接近ML检测性能的同时大大降低复杂度，但其复杂度与球半径和信噪比等参数有关，复杂度不可控，不利于硬件实现。QR分解后M算法(QRD-M)因为固定且较低的复杂度和近似ML算法的性能而成为研究热点。但QRD-M算法要求保留较多的路径，在高信噪比时，复杂度有可能比SD算法更高[2]，此外，QRD-M算法需要对保留路径按照度量值进行排序，排序的复杂度也增加了算法实现的难度。QRD-M也存在检测层顺序的问题，研究人员针对QRD-M算法的优缺点提出了很多改进的算法[3-8]。

本文结合文献[5-6]中算法的优点，并对其进行改进，提出一种低复杂度易于实现的QRD-M搜索算法。通过限制路径扩展点为候选集中的点，在每层扩展时，动态更新SIC检测结果，并将其度量值作为QRD-M树搜索的半径，将SIC的半径限制从反馈机制改为预先设置半径模式，用SE(Schnorr Euchner)搜索策略每层仅搜索在搜索半径内的节点，这样不仅可以避免搜索半径外的节点，同时也可省去排序操作，降低了复杂度。引入可变参数t，即第m层至第t+1层的检测采用SE搜索策略的QRD-M算法，在第t层至第1层采用两种方法共同限制半径的SE搜索策略的QRD-M算法检测，通过选择恰当