基于实时电价预测的智能家居器具优化调度

刘 真，李文竹，任丹萍，刘 心

(河北工程大学 信息与电气工程学院，河北 邯郸056038)

基于实时电价预测的智能家居器具优化调度

刘 真，李文竹，任丹萍，刘 心

(河北工程大学 信息与电气工程学院，河北 邯郸056038)

针对家庭器具优化调度中电价预测误差高和用户舒适度衡量偏差大的问题，提出了一种基于小波、微粒子群和自适应神经网络模糊推理系统(Wavelet-PSO-ANFIS，WPA)电价预测的家庭器具优化调度算法。并在该算法中针对器具运行时长不同的问题，提出了一种新颖的相对量化舒适度的方法。仿真结果表明，此电价预测方法在不牺牲计算复杂度的基础上提高了预测精度，不仅可以权衡用户的用户支付和不满意度，还可以降低系统的峰均比。

实时电价预测；WPA；器具优化调度；相对量化舒适度

1 家庭器具调度系统

需求响应(DR)作为智能电网的重要组成部分，为用户和供应商提供了更多选择，是解决能源价格浮动和能源消耗上涨的一种有效方法[1-2]。DR是通过用户响应电价变化或激励支付，改变其固有的消费模式，减少了用户电力支付，并且保证了系统稳定性[3-5]。用户使用的平均电价模式并不能反应实际的消耗价格，因此，针对平均电价的这种不足，提出了实时电价(RTP)、分时电价(TOU)和尖峰电价(CPP)[6-7]。分时电价和尖峰电价一个季度进行一次管理，电价值是提前设定，但为了真实地反映用户实际消耗和公共事业单位的电价水平，需要每小时进行电价的更新与管理，实时电价具有更高的灵活性，每小时对电价进行更新，符合智能家居[8-9]中通过电价的高低进行器具调度的要求。因此，本文中以实时电价为基础，对家庭器具进行优化调度，家庭器具调度系统如图1所示。

优化调度的前提是预测提前一天的实时电价。电价预测的方法有很多种，主要包括时间序列法，神经网络法和组合方法[10-11]。在文献[12-13]中，采用时间序列法(ARIMA)对电价进行了预测，这种方法需要的历史数据少，计算速度快，但是相比于其他方法预测误差较大；在文献[14]采用神经网络(NN)对实时电价进行电价预测，虽然神经网络方法相比于时间序列法预测精度得到了提高，但是当每个小时电价值的变化相差较小时，仍会影响预测效果。本文为了更加精确地预测实时电价，以西班牙的历史电价为基础[15]，采用小波、微粒子群和自适应神经网络模糊推理系统(Wavelet-PSO-ANFIS，WPA)组合的方法预测实时电价。通过与其他电价预测的方法(ARIMA， W-ARIMA， NN)比较，表明了本文采用的这种电价预测方法在不牺牲计算复杂度的前提下，大大提高了电价预测精度。

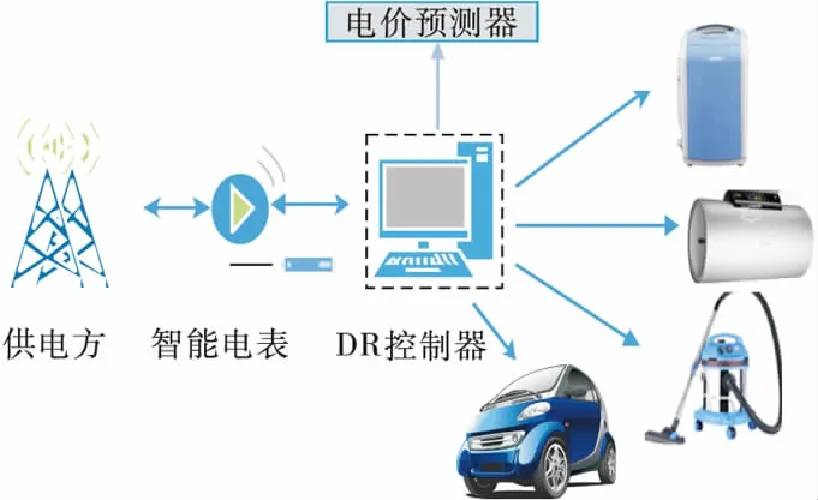
图1 智能家居系统

其次，关于家庭器具的优化调度，学者也在不断的研究。文献[16-17]中通过不同的优化调度方法，减少了用户的电力支付，把保证了系统的稳定性，但是忽略了对用户舒适度的考虑；文献[18]中通过结合可再生能源的可用性预测和市场电价预测技术，为家用电器分配动态优先权，实现智能家居能源消耗的有效管理和调度，但是缺乏节能与体验质量的均衡性考虑与分析；文献[5，19]提出的优化调度算法权衡了用户的电力支付与用户的舒适度。但是以上的研究中均没有考虑器具的特殊性，没有针对家庭中不同器具的特性，考虑用户对不同器具延迟或者提前的影响。

针对器具的工作时长不同，文中提出了一种相对量化用户舒适度的方法，采用该方法解决了用户对不同器具延迟或者提前产生不同敏感度的问题，应用数学方法衡量了用户对不同器具的满意度。本文建立了关于用户电力支付和用户舒适的线性规划模型，通过优化调度有效地权衡了用户的电力支付与用户的舒适度，降低了系统的峰均比，保证了供电方系统的稳定性。

2 实时电价预测

准确的电价预测对于供应商和用户都存在重大意义。供应商利用预测的电价来策略投标，风险评估和制作投资计划等；用户则根据预测的电价重新安排器具。

2.1 利用WPA进行实时电价的一般步骤

WPA方法是一种混合方法，在电价预测中小波、PSO和ANFIS对于提高预测精度各有不同的用途。其中，小波转换将价格序列转换为一系列基本序列，这些基本序列比原始的价格序列表现出更好的性质，因此，可以更加精确地预测。它用在电价预测的第一阶段和最后一阶段。ANFIS结合了NN的自我学习能力和模糊推理的语言表达能力，应用于非线性预测，利用过去的样本来预测未来的样本，而PSO用于提高ANFIS的性能，调整隶属函数来实现低的错误。电价预测的具体步骤如图2所示。

图2 WPA电价预测流程图

第一步：价格序列的分解。对价格序列按照小波分析法进行分解，得到高频序列和低频序列。

第二步：高频和低频序列的预测。对每个序列进行预测时，首先确定PSO的种群大小，用初始化的种群代替ANFIS的前件参数，根据前件参数计算后件参数的值，从而计算网络误差，将该网络误差作为粒子群的适应度值。接着更新粒子的速度和位置从而得到ANFIS的各参数。最后利用ANFIS对这些序列逐步训练以确定最佳模型，通过该模型预测所有序列。

第三步：将预测的序列重构为原来序列的预测值。

2.2 利用WPA预测西班牙的实时电价

本节选取西班牙2013年3月到5月的电价作为训练数据，预测出2013年6月1日07：00到6月2日06：00的24小时的电价。PSO的参数设置如表1所示。图3是利用文中提出WPA方法预测的电价与实际电价的对比图。

表1 PSO的参数设置

PSO参数数值种群大小20加速常数C1和C22迭代次数800初始惯性权重1最终惯性权重05

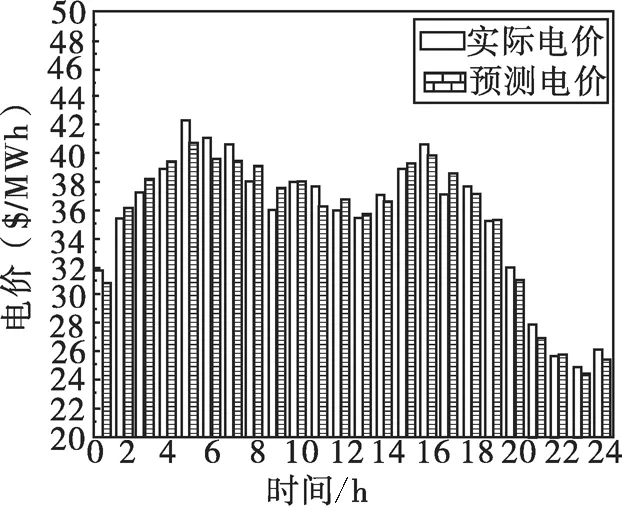
图3 2013年6月1日的实时电价和预测电价

2.3 不同的实时电价预测方法

根据式(1)计算了ARIMA、W-ARIMA、NN和WPA的平均绝对百分比误差(MAPE)。由表2数据可知，文中提出的WPA的预测效果优于其他几种方法。

(1)

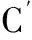
表2MAPE计算结果

预测方法MAPEARIMA667Wavelet-ARIMA611NN591WPA437

2.4 电价模式

为了防止用户在低电价时段开启大量器具，本文中采用实时电价与斜坡块率(IBR)结合的电价模型

(2)

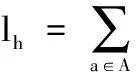
3 优化调度模型

根据器具自身特性和用户的行为习惯，将家庭器具进行分类：非实时器具和实时器具。为了满足用户需求器具运行时间不能延时，当器具到达运行时间后必须马上开启，这类器具被指定为实时器具，例如：电视、电脑、电灯等；而热水壶、洗衣机、电饭煲等家庭器具可以根据所接收到的电价信息调度操作时间，减少电力支付，这类器具被称为非实时器具。将家庭器具的优化调度范围设定为一天(2013年6月1日07：00到6月2日06：00)，利用H表示优化调度空间，则调度时隙 h∈[1，2，…， H]。A表示非实时器具，对于每个器具a∈A，在时隙h的能耗是ea，h。

3.1 目标函数

目标函数的目的是最小化用户的支付成本，包括电力成本和用户舒适度成本。

3.1.1 用户电力支付

在所预测的实时电价基础上，用户的电力成本被公式化为

(3)

3.1.2 用户不满意度

由于家庭中不同器具的工作时长不同，为了权衡用户对不同器具的满意度问题，我们提出了一个量化舒适度的方法，即在用户可以容忍器具的工作时段内，利用优化调度后器具的工作时隙和用户最满意器具的工作时隙的相对距离与用户可容忍器具工作时隙总数之比来表示用户的满意度

(4)

(5)

式中：ψa是器具a优化调度后的实际开启时隙；γa是用户最满意器具a的开启时隙；la是器具a工作完成需要的总时隙数；λa是器具a在舒适度成本中所占的权重，λa=w/la；Za表示用户对器具a的不满意度；Z表示用户的不满意度。

3.2 约束条件

为了满足目标函数，达到最小的用户电力支付成本与用户的舒适度成本，需要满足以下约束条件。

3.2.1 能耗约束

在调度过程中为了保证器具a可以完成操作，所需的能源是

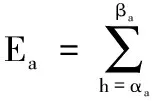
(6)

式中：αa和βa分别表示用户能够容忍的器具a运行的开始时隙和结束时隙；Ea表示器具a完成操作需要的总能耗。

为了保证系统的稳定，每个时隙器具的能耗有限，假设Emax，h为时隙h的最大能耗上限

(7)

3.2.2 舒适度约束

为了保证用户的舒适度，每个器具的不满意度需要小于用户对该器具的最大不满意值m

Za≤m

(8)

3.3 线型规划模型

结合式(3)和式(5)，本文中提出的用户支付的目标函数为

(9)

由于式(9)是不可微分的，所以将目标函数(9)进行优化。结合式(2)，每个时隙的电力支付被重新公式化：

当h时隙家庭器具的能耗0 ≤lh≤Emax，h时，用户的电力支付Pa为

(10)

(11)

因此

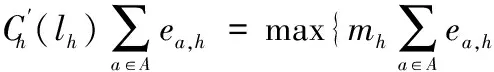
(12)

引入二进制决策变量xa，h，当xa，h= 0表示器具a在时隙h开启；xa，h= 1表示器具a在时隙h关闭。则式(11)被重新公式化为

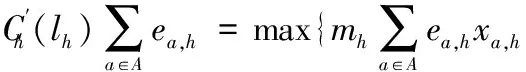
(13)

通过上述变换，所提出的最小支付的调度问题被公式化为如下整数线性规划模型

(14)

式中：w1，w2分别为电力成本与舒适度在成本支付中的权值，w1+w2=1。

4 仿真验证

这一部分，利用计算机软件MATLAB和CPLEX仿真验证来评估提出的基于电价预测的家庭器具优化调度方法的性能。假设住宅在仿真过程中器具的参数设定如表3所示。时隙长度为10min，则时隙t∈T=[1，2，3，…，144]。假设本文中所有器具的运行时间均为用户能够容忍的器具的工作范围。

表3 各种器具开始时间的参数

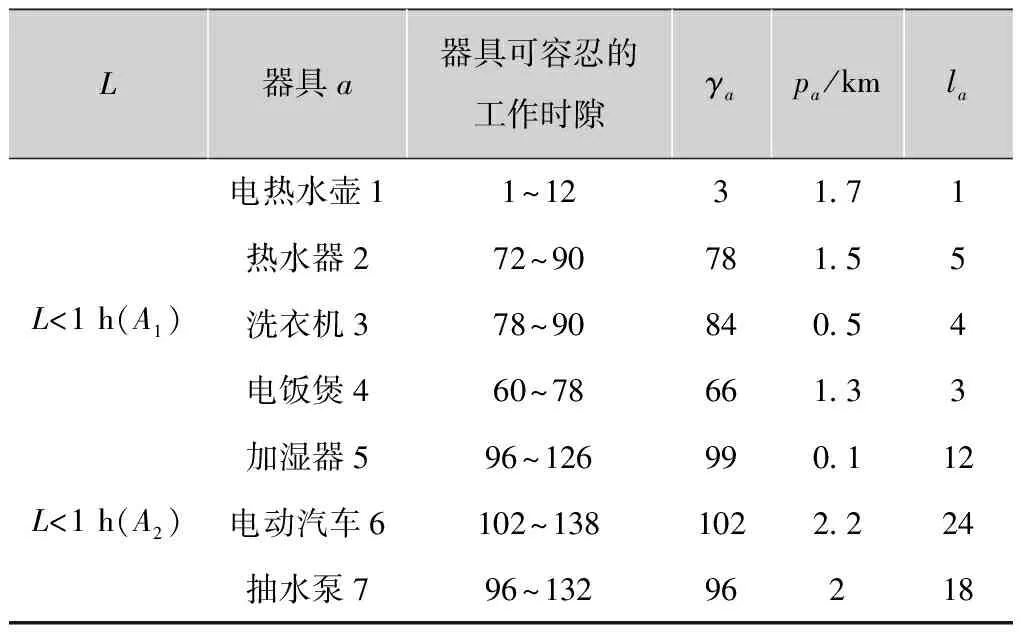
L器具a器具可容忍的工作时隙γapa/kmlaL<1h(A1)电热水壶11～123171热水器272～9078155洗衣机378～9084054电饭煲460～7866133L<1h(A2)加湿器596～126990112电动汽车6102～1381022224抽水泵796～13296218

4.1 电力成本与不满意度的关系

通过表4中的3种案例来说明用户不满意度与电力成本的关系。案例1：首先假设用户对器具的不满意度上限m=2，考虑用户的电力成本，即w1=1，w2=0时，对家庭器具进行优化调度。图4是经过优化调度后器具的实际操作时隙。然后将表3与图4中数据带入式(4)可以得出每个器具的不满意度值，如表5所示。此时，用户的不满意度Z=3.072，用户的电力支付Pa=50.95 cents；案例2：只考虑用户的最小电力成本，不考虑其他两个因素，即w1=1，w2=0时，m可以无限大，则用户不满意度Z=5.357，用户的电力支付Pa=41.39 cents；案例3：不考虑m与Pa，只考虑用户的不满意度，即w1=0，w2=1，此时不满意度Z=0，用户的电力支付为65.89 cents。

表4 案例研究总结

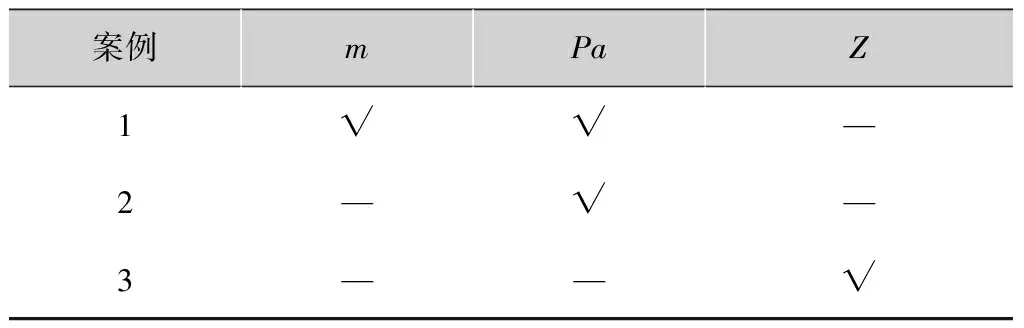
案例mPaZ1√√—2—√—3——√

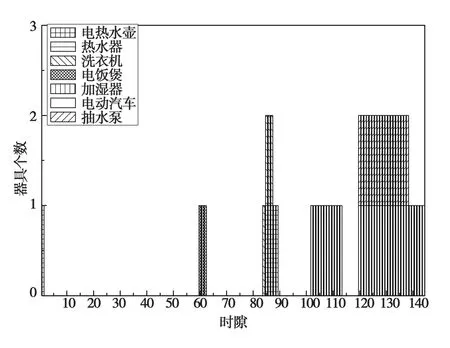
图4 优化调度后器具的工作时隙

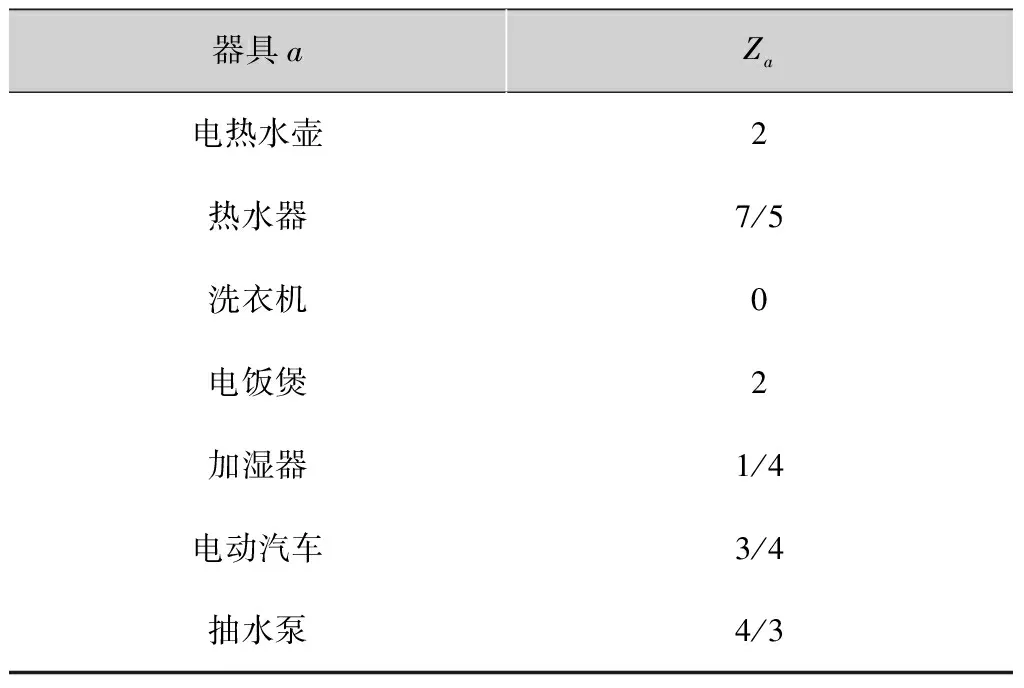
器具aZa电热水壶2热水器7/5洗衣机0电饭煲2加湿器1/4电动汽车3/4抽水泵4/3

通过比较以上3种案例，发现用户的电力支付与用户的不满意度成反比。因此，可以通过对器具的优化调度来权衡用户的电力支付与用户的不满意度。

4.2 量化舒适度的影响

以上一节中案例1为对象说明本文中所提出的相对量化舒适度的性能。根据表 3中的数据可知，电饭煲的实际开启时间比用户最满意的开始时间提前了6个时隙，而电动汽车的实际开启时间比用户最满意的开启时间延后了18个时隙。通过文献[5]中的方法，单从时隙方面来看，电动汽车对用户造成的影响较大。但是，电动汽车的工作时长相比于电饭煲要长，只采用这种方法无法准确衡量用户的满意度。所以采用本文中提出的相对量化方法，可以得出电动汽车的不满意度是3/4，而电饭煲的不满意度为2，如表 5所示。因此，电饭煲开启时间的改变相比于电动汽车对用户的影响较大。

这种针对不同的器具特性，采用相对量化的方法，可以更加准确的衡量出器具延迟或者提前对用户造成的影响，提高用户的舒适度。

4.3 用户的支付成本

以上一节中案例1为例，说明优化调度对系统性能的影响。本节通过用户的电力支付评估文中提出的优化调度方案的性能。图5中显示出优化调度前与优化调度后用户的电力支付从65.89美分降低到50.95美分，降低了22.67%。图6中表明了一个月内用户每天优化调度前与优化调度后的电力支付，一个月内用户的电力支付从20.32美元降低到 15.98美元。

利用式(15)计算系统的分均比可知，通过使用优化调度算法系统的平均PAR从5.65降低到4.57，降低了19.1%。

(15)

仿真结果表明利用文中所提出的优化调度算法不仅可以减少用户的电力支付，还可以降低系统的峰均比，保证系统的稳定性。

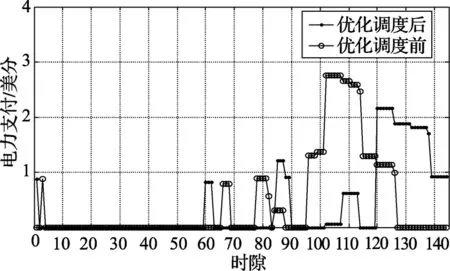
图5 优化调度前与优化调度后用户的电力支付

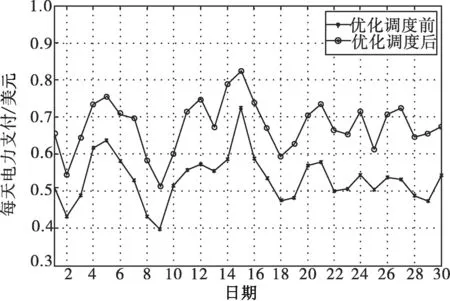
图6 一个月中用户每天的电力支付

5 结束语

本文将WPA电价预测方法应用到智能家居中的实时电价预测。这种方法不仅保证了电价预测的预测精度，还保证了所预测电价的实时性。在预测的实时电价基础上，提出了一种家庭器具的优化调度算法，权衡了用户的电力支付与用户的舒适度问题，并且在文中提出了一种相对量化舒适度的方法，解决了器具由于工作时长不同，造成的用户对不同器具延迟或者提前工作产生不同影响的问题。

[1] TRIPLET M. The market for demand response-the DR maturity model perspective[J]. Power Engineering， 2013， 117(5)： 14-14.

[2] Smart Grid[EB/OL].[2015-04-12].http：//energy.gov/oe/technology-development/smart-grid.

[3] YI P， IWAYEMI A. Real-time opportunistic scheduling for residential demand response[J]. IEEE Trans. Smart Grid，2013，4(1)：227-234.

[4] PALENSKY P， DIETRICH D. Demand side management： demand response， intelligent energy systems， and smart loads[J]. IEEE Trans. Industrial Informatics， 2011， 7(3)： 381-388.

[5] SETLHOLO D， XIA XiaoHua， ZHANG JiangFeng. Optimal scheduling of household appliances for demand response[J]. Electric Power Systems Research， 2014(116)：24-28.

[6] 田世明，王培培，张晶.智能电网下的需求响应关键技术[J].中国电机工程学报，2014，34(22)：3576-3589.

[7] 罗达， 付蔚， 蔡林沁，等. 一种智能家居系统的集群识别调度的研究[J].电视技术， 2012， 36(19)： 8-10.

[8] 朱敏玲，李宁. 智能家居发展现状及未来浅析[J].电视技术，2015，39(4)：82-96.

[9] 马晓槟.智能家居，智慧生活[J].电视技术，2014，38(SI)：54-66.

[10] 张显，王锡凡.短期电价预测综述[J].电力系统自动化，2006，3(3)：92-101.

[11] 邓佳佳，黄元生，宋高峰.基于非参数GARCH的时间序列模型在日前电价预测中的应用[J].电网技术，2012，36(4)：190-196.

[12] NOGALES F J， CONTRERAS J， CONEJO A J. Forecasting next-day electricity prices by time series models[J]. IEEE Trans. Power Systems， 2002， 17(2)：342-348.

[13] CONEJO A J， PLAZAS M A， ESPINOLA R. Day-ahead electricity price forecasting using the wavelet transform and ARIMA models[J].IEEE Trans. Power Systems， 2005， 20(2)：1035-1042.

[14] CATALAO J P S， MARIANO S J P， MENDES V M F. Short-term electricity prices forecasting in a competitive market： a neural network approach[J]. Electric Power Systems Research， 2007， 8(6)：1297-1304.

[15] Market operator of the electricity market of mainland spain[EB/OL].[2015-04-12]. http：//www.omel.es/.

[16] CHAVALI P，YANG P，NEHORAI A. A distributed algorithm of appliance scheduling for home energy management system[J]. IEEE Trans. Smart Grid， 2014，5(1)：282-290.

[17] LIU Xin， IVANESCU L， KANG R， et al. Real-time household load priority scheduling algorithm based on prediction of renewable source availability[J]. IEEE Trans. Consumer Electronics， 2012， 58(2)：318-326.

[18] MOHSENIAN-RAD A H， WONG V W S， JATSKEVICH J. Autonomous demand side management based on game theoretic energy consumption scheduling for the future smart grid[J]. IEEE Trans. Smart Grid， 2010， 1(3)：320-331.

[19] MOHSENIAN-RAD A H， GARCIA A L. An optimal power scheduling method for demand response in home energy management system[J]. IEEE Trans. Smart Grid， 2013， 4(3)：1391-1400.

责任编辑：时 雯

Optimal Scheduling Method of Appliances Based on Real-time Electricity Price Forecasting in Smart Home

LIU Zhen，LI Wenzhu，REN Danping， LIU Xin

(School of Information and Electric Engineering， Hebei University of Engineering，Hebei Handan 056038， China)

Aiming at the problem of the high error of price forecasting and the low accuracy of user satisfaction in optimal scheduling of appliances， an optimal scheduling algorithm of appliances based on a novel hybrid approach is presented， combining wavelet transform， particle swarm optimization， and adaptive-network-based fuzzy inference (Wavelet-PSO-ANFIS， WPA) system. In addition， according to appliances’ different length of operation time， a relative quantitative method of user comfort is proposed to measure user satisfaction of different appliances. Simulation results show that the proposed electricity price forecasting method presents better forecasting accuracy with an acceptable computation time. The proposed optimal scheduling method of household appliances can benefit both users， by balancing their electricity cost and user satisfaction， and utility companies， by reducing the peak-to-average ratio.

real-time electricity price forecasting； WPA； optimal appliances scheduling； relative quantitative method of user’s comfort

国家自然科学基金项目(61440001)；教育部新世纪优秀人才支持计划项目(NCET-13-0770)；河北省高等学校高层次人才科学研究项目(GCC2014062)；河北省高等学校科学技术研究项目(ZH2012020；QN20131064)

TP273

A

10.16280/j.videoe.2015.20.011

刘 真(1990— )，女，硕士生，主要研究方向为智能电网；

李文竹(1979— )，女，硕士，助教，主要研究方向为智能电网、宽带接入；

任丹萍(1984— )，女，讲师，博士，主要研究方向为光纤无线混合接入网络；

刘 心(1980— )，教授，博士后，主要研究方向为智能电网、下一代光网络与宽带接入。

2015-05-15

【本文献信息】刘真，李文竹，任丹萍，等.基于实时电价预测的智能家居器具优化调度[J].电视技术,2015，39(20).