新分数阶混沌系统的线性反馈控制及投影同步分析

王宝贤, 张艳杰

(1. 三峡大学 理学院，湖北 宜昌 443002；2. 国网技术学院，山东 济南 250002)



新分数阶混沌系统的线性反馈控制及投影同步分析

王宝贤1, 张艳杰2

(1. 三峡大学 理学院，湖北 宜昌 443002；2. 国网技术学院，山东 济南 250002)

为探求分数阶混沌系统的混合投影同步的实现机理，基于一类新的分数阶混沌系统和Lyapunov稳定性理论，采用线性反馈控制方法将系统的混沌运动状态控制到稳定态，系统达到控制目标时，控制增益只需要满足线性矩阵不等式，且控制策略简洁易于实现。并将结论应用到投影同步中，得到了分数阶混沌系统实现混合投影同步的控制增益的必要条件。通过Matlab数值仿真，分析了不同的投影因子矩阵情形下的混沌同步，验证了控制策略与同步方法的可行性。

反馈控制；分数阶混沌系统；混合投影同步；Lyapunov稳定性；渐近稳定

王宝贤,张艳杰.2015.新分数阶混沌系统的线性反馈控制及投影同步分析[J].东华理工大学学报：自然科学版，38(4)：454-457.

Wang Bao-xian, Zhang Yan-jie.2015.Linear feedback control and projective synchronization of a new fractional-order chaotic system[J].Journal of East China Institute of Technology (Natural Science), 38(4)：454-457.

混沌现象是现实世界中普遍存在的非线性现象，在物理学、生物学、经济学等领域均发现了混沌现象，由于混沌系统在保密通信、信号处理等领域的广泛应用，近年来对混沌系统的研究达到顶峰。至今已发现多种经典整数阶混沌系统，如Lorenz系统，Rossler系统等。随着分数阶微积分理论的发展，分数阶微积分模型能更好地描述自然界中的物理机制及其变化规律，众多学者发现了一系列更具丰富混沌现象的分数阶混沌系统。如多涡卷混沌系统均具有两个或两个以上的涡卷，比单涡卷系统具有更加复杂的拓扑结构及更丰富的动力学行为，已经成为混沌研究领域的新热点。文献Wang(2009)提出了每项微分方程均包含一个二阶非线性项的一个新的三维自治多涡卷混沌系统，选取不同参数可产生单涡卷，双涡卷，三涡卷及四涡卷混沌吸引子。Chen等(2013)在此基础上推广到分数阶系统，发现当阶数低于3时，该系统同样存在与整数阶系统类似的动力学行为。混沌同步由于在保密通信领域(吕冰等，2012)有着潜在的应用价值，成为非线性科学领域研究热点之一。Zhou等(2011a)提出了一类新型混合函数投影同步，其中投影因子为与驱动系统状态相关的有界函数。刘景琳(2014)基于分数阶系统稳定性理论，该文通过设计自适应控制器和参数更新率，提出了一种自适应混合函数投影同步方案。Wu等(2012)研究了一类新的分数阶超混沌系统动力学行为，同时研究了相应的修正投影同步。混合投影同步(Chang et al.,2010; Zhang et al.,2012；Zhou et al.,2011b;吴耿等，2008；王亚民等，2013；Kengne et al.,2013; Monje et al.,2010)在混沌保密通信中有着更好的抗破译功能，于是研究分数阶混沌系统的同步是有意义的。

1 分数阶微积分

分数阶算子是整数阶算子的推广，至今分数阶微分算子通常有三种定义：Grunwald-Letnikov定义，Riemann-Liouville定义与Caputo定义。考虑如下分数微分方程：

Dqx(t)=f(x(t))

(1)

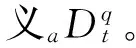
引理1 对分数阶系统(1)，当分数阶数q≤1，若存在实对称正定矩阵P，使得对任意状态变量x，函数J=xTPDqx≤0恒成立，则系统(1)渐近稳定(Zhao et al.,2010)。

2 新分数阶混沌系统模型

考虑如下新分数阶混沌系统模型(Chen et al.,2013)：

(2)

本文中仿真均采用预估-校正法(Zhou et al.,2005)。当参数取a=1.46,b=9,c=5,d=0.06及分数阶阶数q=0.95，系统(2)存在混沌现象。

3 线性反馈控制

设计采用线性反馈控制器如下：

(u1u2u3)=(k1x1k2x2k3x3)

(3)

相应受控系统为

(4)

定理1 若存在线性反馈控制增益K=diag(k1,k2,k3)，使得

(5)

成立，则受控系统(4)是渐近稳定的。

xTPDqx=(x1,x2,x3)P(Dqx1,Dqx2,Dqx3)T=

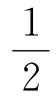
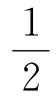
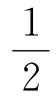
由(5)知xTPDqx=xTΦx≤0成立，所以根据引理1，知系统(4)是渐近稳定的。

这里采用的方法可以推广到其他类似类型中，如分数阶Newton-Leipnik系统(Zhangetal.,2012)。

4 投影同步

形如(1)的分数阶系统都可以写成如下形式：

Dqx=Ax+g(x)

(6)

其中A为系统的线性部分矩阵，g(x)=(g1(x),…,gn(x))T∈Rn为其系统的非线性部分。考虑(6)作为驱动系统，则其对应的响应系统为：

Dqy=Ay+g(y)+u(x,y),

(7)

其中，u(x,y)=(u1(x,y),…,un(x,y))∈Rn为实现全状态的混合投影同步的控制器。定义误差为e=y-Λx∈Rn，其中Λ称为投影同步的投影因子矩阵，则误差系统为

Dqe=Dqy-ΛDqx=Ay-ΛAx+g(y)-Λg(x)+u(x,y).

根据误差的定义，上式可以简化为如下形式：

(8)

若矩阵Λ=I，I为单位矩阵，则该同步称为完全同步；若Λ=-1，称为反相同步；若Λ=al,a≠±1且非零实数，称为投影同步；若Λ=diag(λ1,λ2,…,λn)，且λ1,λ2,…,λn是不相同的非零常数，称为修正投影同步。上述同步定义均是该文混合投影同步的特例。

推论1 若选取控制器

u(x,y)=(ΛA-AΛ)X-g(y)+Λg(x)+g(e)+Ke,

(9)

其中K=diag(k1,k2,k3)为常实数矩阵。若反馈控制增益K满足(5)，则驱动系统(6)与响应系统(7)实现混合投影同步。

证明：将控制器(9)代入误差系统(8)得

Dqe=Ae+g)(e)+Ke

(10)

5 数值仿真

仿真中初始值为x(0)=(7.4777,-4.1685,-5.3684)T，y(0)=(0.5,0.5,0.5)T，且控制器均为K=diag(-2,2,3)。系统参数均取为a=1.46,b=9,c=5,d=006。对受控系统(4)，控制增益K作用下其混沌状态均快速收敛到稳定态(图1)。

图1 驱动系统与响应系统的混合投影同步误差曲线Fig.1 Synchronization error between drive system and response system

针对混合投影同步，若选取投影因子矩阵分别为=Λdiag(0.3,0.3,0.3)与=Λdiag(2,0.5,1)，则其对应的驱动系统与响应系统的相图如图2-3所示。

图2 驱动系统与响应系统相图Fig.2 Phase portrait of drive system and response system

图3 驱动系统与响应系统相图Fig.3 Phase portrait of drive system and response system

6 结论

本文通过构造一类特殊的矩阵，基于Lyapunov稳定性理论，采用线性反馈控制方法实现新的分数阶系统的稳定化，得到了系统达到控制目标时控制增益所满足的条件。同时得到了系统实现混合投影同步的控制增益的必要条件。最后通过Matlab仿真研究了不同的投影因子矩阵情形下投影同步，验证了所采用的控制策略的可行性。

刘景琳. 2014. 不确定参数分数阶Lorenz混沌系统的混合函数投影同步[J]. 华南师范大学学报：自然科学版, 46(2): 38-41.

吕冰, 朱长江. 2012. 分数阶超混沌系统的耦合广义投影同步及其在保密通信中的应用[J]. 河南大学学报：自然科学版, 42(3): 302-308.

王亚民, 朱鑫铨, 姬天富, 等. 2013.不同阶异结构分数阶混沌系统的广义投影同步[J]. 扬州大学学报:自然科学版, 16(4): 22-25.

吴耿, 丰建文, 张维强. 2008. 分数阶Genesio系统的混沌同步[J]. 三峡大学学报：自然科学版, 30(4): 106-109.

Chang C M, Chen H K.2010. Chaos and hybrid projective synchronization of commensurate and incommensurate fractional-order Chen-Lee systems[J]. Nonlinear Dynamic, 62: 851-858.

Chen F, Xia L, Guo D Q, et.al. 2013. A Fractional-order Multi-scroll Chaotic System[J]. Journal of Information & Computational Science 10(4): 1203-1211.

Kengne R, Tchitnga R,Tchikankou A N,et.al. 2013. Dynamical Properties and Finite-Time Hybrid Projective Synchronization Using Fractional Nonsingular Sliding Mode Surface in Fractional-Order Two-Stage Colpitts Oscillators[J]. Journal of Chaos, Article ID 839038.

Monje C A,Chen Y Q, Vinagre B M, et.al. 2010. Fractional-order Systems and Controls: Fundamentals and Applications[M], London: Springer:218.

Wang L. 2009. 3-scroll and 4-scroll chaotic attractors generated from a new 3-D quadratic autonomous system[J]. Nonlinear Dynamics, 56(4): 453-462.

Wu X J,Wang H,Lu H T. 2012. Modified generalized projective synchronization of a new fractional-order hyperchaotic system and its application to secure communication[J]. Nonlinear Analysis: Real World Applications, 13: 1441-1450.

Zhang K, Wang H,Fang H. 2012. Feedback control and hybrid projective synchronization of a fractional-order Newton-Leipnik system[J]. Commun Nonlinear Sci Numer Simulat, 17: 317-328.

Zhao L D, Hu J B,Liu X H. 2010. Adaptive tracking control and synchronization of fractional hyper-chaotic Lorenz system with unknown parameters[J]. Acta Physica Sinica, 59: 2305-2309.

Zhou P, Yang X Y.2011a.A Novel Hybrid Function Projective Synchronization between Different Fractional-Order Chaotic Systems[J]. Discrete Dynamics in Nature and Society, Article ID 496846.

Zhou P,Zhu W.2011b. Function projective synchronization for fractional-order chaotic systems[J]. Nonlinear Analysis: Real World Applications, 12: 811-816.

Zhou T S,Li C P. 2005. Synchronization in fractional order differential systems[J]. Physica D: Nonlinear Phenonmena, 212(1/2): 111-125.

Linear Feedback Control and Projective Synchronization of a New Fractional-order Chaotic System

WANG Bao-xian1, ZHANG Yan-jie2

(1. China Three Gorges University, College of Science, Yichang HB, 443002, China; 2. State Grid of China Technology College, Jinan SD, 250002, China)

The mechanism of the hybrid projective synchronization of a new fractional-order chaotic system on the basis of the Lyapunov stability theory is explored. By the method of linear feedback control, chaotic states are controlled to the stable states and the crita for control gain are derived. The control gain matrix only needs to statisfy the condition of the linear matrix inequality and the method is easy to implement. The results are also applied to the projective synchronization of a new fractional-order chaotic system and a necessary condition for control gain to achieve the hybrid projective synchronization is obtained. Finally, the chaotic synchronization with different projective matrix is analyzed and the feasibility of control strategy and synchronization method is verified via MATLAB numerical simulation.

feedback control; fractional-order chaotic system; hybrid projective synchroniztion; Lyapunov stability; asymptotic stability

2015-03-24

国家自然科学基金项目(61304162)；三峡大学科研启动基金(KJ2012B075)

王宝贤(1981—), 女, 博士, 讲师, 主要从事非线性控制、性能分析等研究工作。E-mail: bxwang2012@126.com

10.3969/j.issn.1674-3504.2015.04.019

TP13

A

1674-3504(2015)04-0454-04