考虑分布式电源随机性的配电网最大供电能力

张李明，齐先军

(合肥工业大学电气与自动化工程学院，合肥市230009)

考虑分布式电源随机性的配电网最大供电能力

张李明，齐先军

(合肥工业大学电气与自动化工程学院，合肥市230009)

随着分布式电源(distributed generation，DG)越来越广泛地应用，逐渐接入到配电网中，对配电网影响举足轻重，而目前配电网最大供电能力(load supplying capability，LSC)的计算方法均未计及DG接入带来的随机性影响。针对这一问题，首先建立LSC求解模型，在蒙特卡罗模拟的概率潮流计算中考虑DG随机性，利用改进的负荷倍数法和计及电压与支路功率约束的LSC逼近法来计算配电网最大供电能力；然后通过配电网IEEE-33算例验证该模型和算法的有效性，模拟多种情景下LSC的变化，仿真结果表明DG接入配电网可提升网络静态安全裕度，且DG随机性出力影响LSC的分布特征；最后分析制约LSC提升的薄弱环节，并建议在节点电压较低处增加调压装置或无功自动补偿装置。

分布式电源；随机性；最大供电能力；改进的负荷倍数法；电压和支路功率约束

0 引 言

配电网最大供电能力是指在配电网中任意设备均不过负荷条件下，网络所能供应的最大负荷[1]。一般可从2种角度来定义和评价配电网最大供电能力，一是“基于主变互联、满足N-1准则和实际约束”的区域最大供电能力(total supply capability，TSC)；另一是“基于当前实际配电网结构和负荷分布”的最大负荷供应能力(load supplying capability，LSC)。

目前，大多数文献[2-6]对配电网最大供电能力的研究主要集中在TSC这一层面，并提出了具体求解的模型及相关指标的定义[4-6]，该层面的方法可以在负荷未知条件下计算满足N-1安全约束的配电网最大供电负荷，从整体上把握区域供电能力，但其对局部网络(具体到每条馈线)最大供电能力的求解并不是基于现有负荷分布和实际配电网结构，不能真实反映最大供电能力大小。而LSC是从负荷角度反映配电网供电能力是否充足，可作为衡量网络静态安全裕度的指标，能确定性分析当前局部网络的最大供电能力，然后通过叠加得出该区域综合最大供电能力。LSC源于Loadability[7-9]，但LSC对应整个研究区域的Loadability。大多数文献对Loadability的概念描述均是从transmission loadability(或line loadability)方面考虑，主要研究如何提高输电线路的载荷能力，一般是基于热稳定特性和系统安全约束(如电压水平、线路电流、传输损耗、稳定性和温升)对Loadability进行计算分析。目前已有文献研究了无功补偿能力[10]及分布式电源(distributed generation，DG)接入对Loadability的影响。如文献[11-12]分析了DG出力对节点电压的影响，并作出典型节点的PV(有功功率-电压幅值)曲线，以此反映DG配置对Loadability的作用效果，但并没有文献直接对含有DG的LSC进行求解。

常见求解LSC方法有内点法、尝试法以及最大负荷倍数法等[13-15]，但其结果精确性不高。文献[14]提出改进的负荷倍数法使求解LSC模型的节点负荷按照各自的发展速度增长，贴合实际，提高了精度，文献[15]则更加细化，提出将负荷按照其特性(居民区、办公大楼、商业区等)进行分类，各类别服从不同的增长模型；文献[16]提出基于直流潮流的线性规划模型，但该模型仅适用于城市高压配电网且不需精确计算的情况，对中低压配电网不适用；而文献[14-16]均未计及DG的影响。文献[17]虽考虑了含DG的配电网最大供电能力计算，但它是基于主变互联求得各馈线总负荷值(即TSC)，然后将各馈线总负荷值均匀分配到各负荷点进行N-1安全校验逼近，同时假设DG输出功率可控，并没有计及各负荷点的负荷增长特性和DG出力的随机性特征等。

潮流计算是求解LSC的基础，由于DG出力的不确定性，需考虑随机变量带来的复杂变化，常采用概率潮流方法。本文在已有文献[13-17]研究的基础上引入各负荷点负荷分类增长机制，并考虑DG出力随机性，以馈线侧配电网满足负荷最大增长年限为目标，蒙特卡罗抽样模拟的概率潮流计算为基础，并利用改进的负荷倍数法以及计及电压和支路功率约束条件计算LSC。文中设置了多种情景模式，通过对比分析各种情景下的结果，探讨DG位置、类型和出力随机性等对LSC的分布影响，发现限制LSC提升的薄弱环节，并提出合理性建议。

1 配电网最大供电能力模型

1.1 TSC与LSC的联系与区别

TSC与LSC均可作为配电网最大供电能力指标，其联系与区别见表1。

表1 TSC与LSC的对比Table 1 Relation and difference between TSC and LSC

1.2 LSC模型

传统的最大负荷倍数法是假设所有负荷按照同一速度增长，准确性受到影响，本文LSC计算模型引入文献[14-15]提出的改进负荷倍数法。因为对于实际电网而言，各节点当前负荷是已知的，且可以通过历史数据预测各自增长速度。

考虑到配电网各负荷节点一般装有无功补偿装置，因而LSC值以最大供应负荷的有功功率表示，LSC模型计算公式如下:

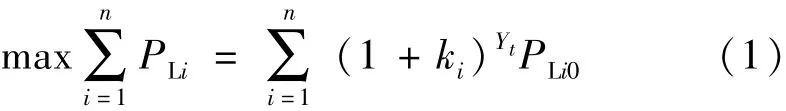
式中:PLi为节点i的有功负荷；ki为节点i的负荷年增长率；PLi0为节点i的初始有功负荷；Yt为负荷增长年限。

由于负荷的波动性，其值可看成是一个随机变量，通过各节点负荷服从的概率分布采用蒙特卡罗抽样可得到其确定的负荷初值，对式(1)进行优化，可以将目标函数转化为求解所有节点负荷同时增长的最大年限为变量的单变量优化目标，即求max Yt。

约束条件:

(1)系统功率平衡约束。

式中:PS、PG、PL分别为研究区域内配电系统中大电网侧有功功率、分布式电源有功出力及负荷总的有功功率；QS、QG、QL分别为大电网侧无功功率、分布式电源无功出力及负荷总的无功功率。

(2)节点电压和支路功率约束。

式中:Ui、Ui.max及Ui.min分别为节点i的电压及电压上下限；Bl、Bl.max分别为支路l的潮流及支路容量。

(3)DG出力约束。

由于DG出力具有不确定性，在接入配电网进行供电能力计算时无法获得准确的出力信息，本文采用概率形式的最大值约束来反映DG的不确定性，即

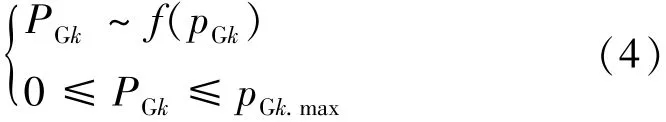
式中:PGk为第k个DG的随机变量，其服从f(pGk)的概率分布；pGk.max表示第k个DG出力最大值。

2 LSC计算

2.1 分布式电源建模

2.1.1 光伏系统的概率模型

在给定光照强度情况下，光伏总的输出功率可以用式(5)表示:

式中:PPV表示光伏(photovoltaic，PV)系统出力，W；r为光照强度，W·m-2；A为光伏系统的总面积，m2；η为光伏系统的转换效率。

据统计，在一段时间内太阳光照强度可以近似看成Beta分布[18]，因而根据光照强度与光伏有功出力的函数关系，推导得到光伏系统有功出力的概率密度函数为

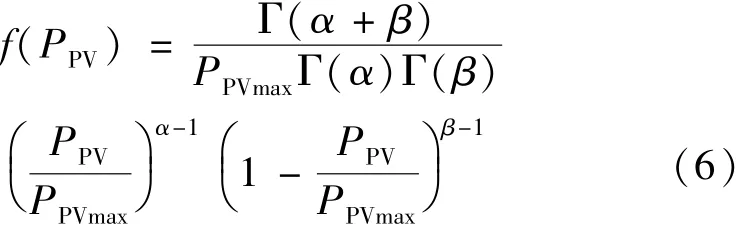
式中:PPVmax＝Aηrmax为光伏发电的最大输出功率；rmax为最大光照强度；α、β为分布参数；Γ为Gamma函数。

为简化计算，考虑DG电源点无功自动补偿装置，可忽略配电网功率因数的变化，将光伏发电看作是注入功率的PQ节点，而无功功率QPV通过接入点恒定的配电网功率因数cosφPV得到，即QPV＝

2.1.2 风电系统的概率模型

风电系统模型的建立离不开对风速的统计，而反映风速统计特性的一个重要形式是风速的频率分布[19]。普遍认为双参数Weibull分布适用于风速统计的描述，因为其形式简单且与实际风速分布能较好拟合。

设某风电场的风速序列(v1、v2，…，vN)服从双参数Weibull分布，推导得到双参数Weibull分布的概率密度函数为

式中:v为给定风速，m·s-1；k为形状参数；c为尺度参数。运用逆变换法可以生成Weibull分布的随机数。

通常根据风机制造商提供的功率特性曲线或者利用公式(8)可以推算出对应风速下的风机出力，即

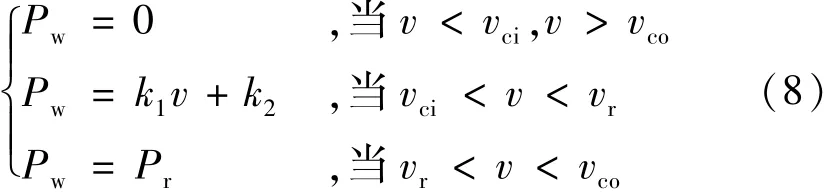
式中:Pw为风机实际出力，kW；Pr为风机额定功率，kW；vr为风机额定风速；vci为风机切入风速；vco为风机切出风速；k1＝Pr/(vr-vci)；k2＝-k1vci。

目前，接入电网的风电机组要求其具备协调控制机组和无功补偿装置的能力，能够保证无功功率有一定的调节容量，所以风电系统能够按恒功率因数cosφw运行，其无功功率Qw可以表示为

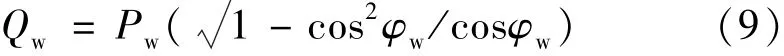
2.1.3 负荷概率模型

配电负荷具有时变性，多数有关概率潮流的文献均将负荷预测结果看成一个随机变量，并采用正态分布近似反映负荷的不确定性，这一点在长期的实践中也得到了验证[19]。设负荷的有功和无功参数分别是μP、σP和μQ、σQ，其值可采用负荷预测方法来确定，则负荷有功和无功的概率密度函数分别为:

2.2 LSC计算步骤和程序流程图

本文采用基于概率潮流计算的LSC逼近法，其在优化问题上具有对目标值试探性逼近和对约束条件的后验式满足的典型特点[20]。该方法计及了电压和支路功率约束对LSC的影响，由于结合了当前实际配电网结构和负荷值，相对于其他模型比较精确，计算步骤如下。

步骤1:读入数据。

步骤2:DG出力、负荷初值的抽样。

根据DG出力和负荷的概率分布，进行蒙特卡罗模拟抽样[21]，通过产生服从上述概率分布的随机数来模拟DG输出功率和负荷大小，形成一个既定网络下确定的DG出力和负荷初值。

步骤3:负荷增长的计算。

利用改进的负荷倍数法，按各负荷点负荷分类的不同增长机制设置负荷增长率，同时设置负荷增长年限步长h。为了计算精确，需考虑负荷无功对潮流计算的影响，则通过式(12)计算各负荷点增长后的负荷大小，即

式中:为节点i增长后的负荷大小(复功率)；为节点i负荷初值(复功率)。

步骤4:采用计及电压和支路功率约束的LSC逼近法计算最大供电能力。

在负荷增加的同时，对全网进行潮流计算，判定各节点电压和支路功率是否越限，若不越限，则继续增加负荷值，若越限，则适当减少负荷的增加，然后重新进入潮流循环计算，直至满足各约束条件(包括节点电压约束、支路功率约束、增长年限精度值约束)为止，此时Yt即为该次抽样下负荷最大增长年限值。另本文中确定性潮流计算采用改进牛顿法[20]，编程简便，收敛速度快，且处理环网能力强。

步骤5:重复步骤2～4，计算得到各次抽样下LSC样本值。

步骤6:对LSC样本进行统计分析，求取均值和均方差，并将其作为随机变量LSC的数学期望和均方差估计。Matlab编写的程序流程如图1所示。

3 算例分析

3.1 算例

本文采用图2所示的IEEE-33节点配电网结构(虚线表示联络线)作为算例(详细参数见附录)，按深度优先搜索算法[20]进行节点编号，假设各负荷点均装有无功就地补偿装置，负荷符合正态分布的随机变量，以各节点负荷PLi、QLi为均值，以0.1PLi、0. 1QLi为均方差。其中基准电压为12.66 kV，基准容量为10 MVA，假设各分布式电源点的功率因数恒为0.90，节点电压上下限分别为1.05 pu和0.85 pu，支路功率最大允许值为7 MVA。

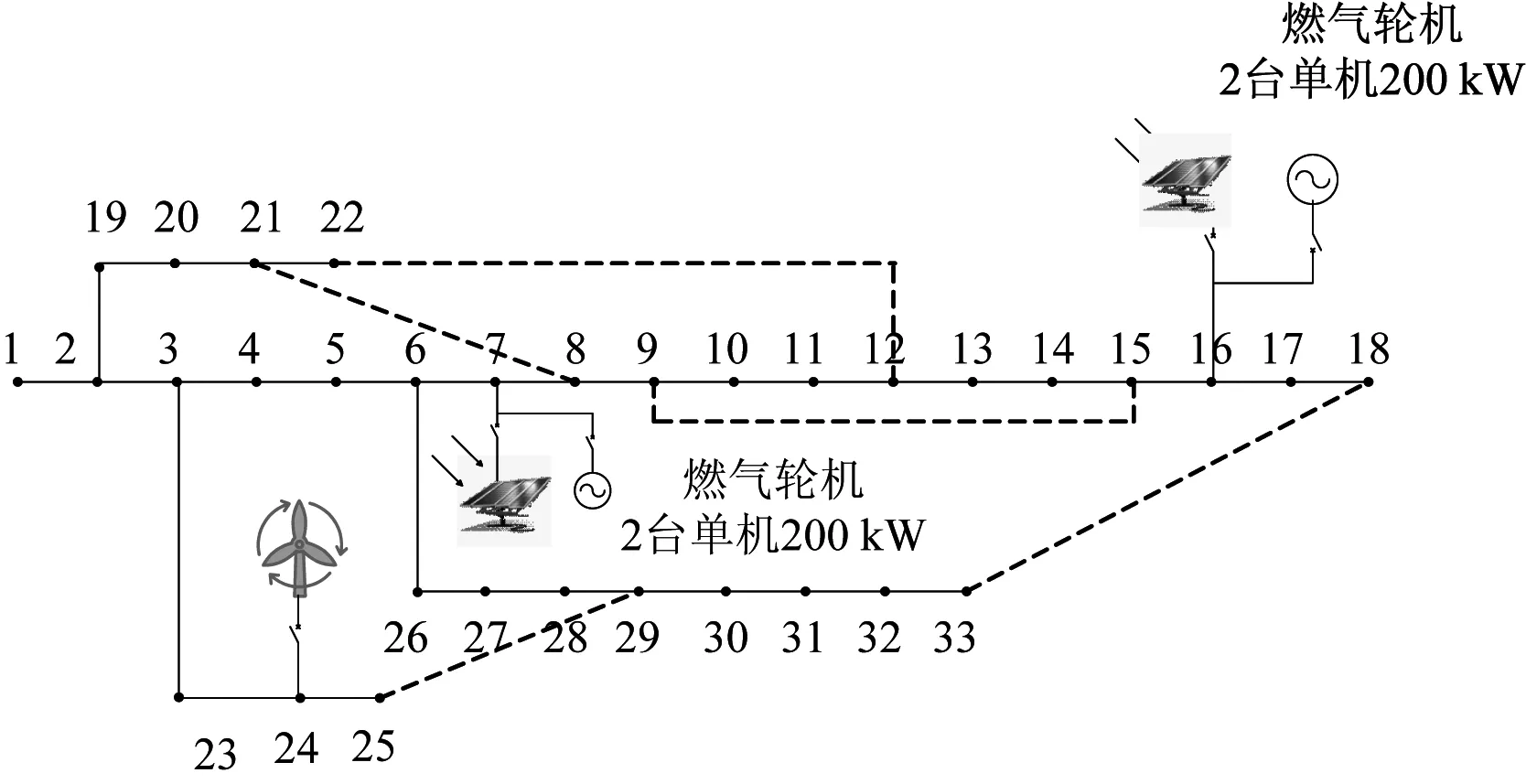
图2 算例结构示意图Fig.2 Schematic diagram of example structure

设1～10号节点的负荷年增长率为10%，11～25号节点为12%，26～33号节点为15%。

另根据文献[19，20，22]的研究成果，DG一般安装在负荷较大点或者靠近馈线中末端比较合适，本文选择在节点7、24和节点16处分别安装光伏发电系统及风力发电系统，表2、3分别列出了光伏系统和风电系统的数据，为了便于比较，在节点7，16各安装2台单机200 kW出力稳定的微型燃气轮机作为对此，对以下几种情景模式分别探讨。

Case 1:该配电网系统不接入DG；

Case 2:仅节点7接入微型燃气轮机发电系统；

Case 3:仅节点16接入微型燃气轮机发电系统；

Case 4:仅节点7接入光伏发电系统；

Case 5:节点7，16接入光伏发电系统，节点24接入风力发电系统。

3.2 结果与分析

本文中蒙特卡罗抽样次数为10 000次，改进牛顿法潮流计算的迭代精度为10-5，负荷增长年限Yt初值及迭代步长h分别设为0和0.5，负荷最大增长年限精确到10-3。5种情景模式下负荷最大增长年限和LSC值大小见表4，LSC概率密度分布如图3所示。

表3 风电系统数据Table 3 Data of wind power system

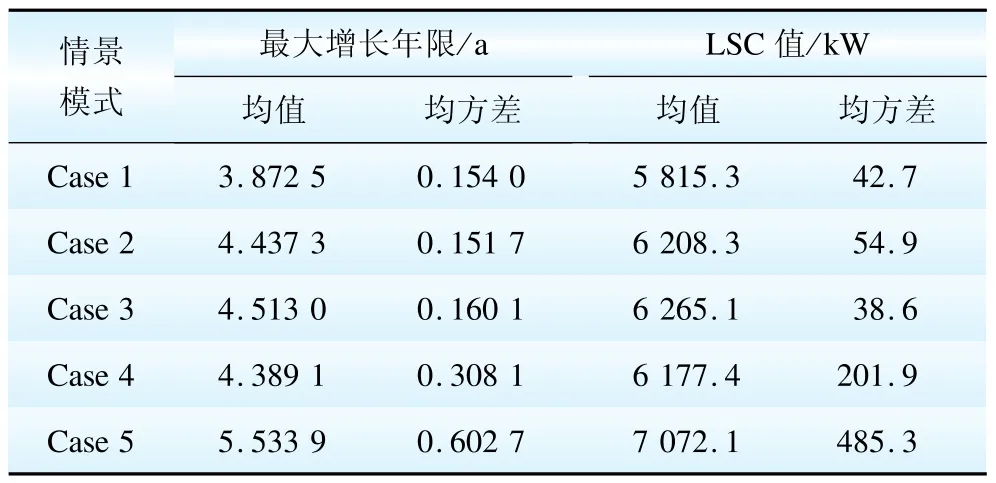
表4 各情景下负荷最大增长年限和LSC值Table 4 Maximum load growth years and LSC value in different scenarios

图3 各情景下LSC概率分布图Fig.3 Probability distribution chart of LSC in different scenarios

据抽样统计，当前配电网结构下总负荷(有功功率)均值、均方差分别为3 715.4 kW和83.91 kW，与表4中LSC相比，整个网络属于轻载状态，其静态安全裕度分别达到约56.5%、67.1%、68.6%、66.3%、90.3%，这说明当前的配电网架构对主网的消纳吸收仍有潜力，而DG对网络静态安全裕度的提升作用较大。对比图3中5种情景的LSC概率分布可知DG接入使得LSC分布在较大值区间的概率增大，且通过表4计算得到Case2～Case5中LSC较Case1(未接入DG)分别提升约6.8%、7.7%、6.2%、21.6%，这表明DG接入能有效提高配电网供电能力；采用非参数假设检验的Jarque-Bera法对LSC数据进行正态分布校验，结果显示LSC近似服从正态分布特点，正好与配电负荷分布特征相匹配。因此，针对含随机性DG的配电网在接入负荷时，需考虑负荷变化与LSC分布特征相统一的原则，以保证供电能力得到充分利用和保持较大的网络静态安全裕度。

以上5种情景方案中，Case 2接入的是稳定出力的微型燃气轮机，Case 4则是出力随机性较强的光伏系统，Case 5则是光伏和风电系统的混合型DG，Case 2、Case 4及Case 5数据结果的均方差对比可知混合型DG波动性最大，其次是光伏系统，微型燃气轮机最小，原因是由于微型燃气轮机出力均衡，其波动主要是由于配电负荷的时变性引起的，而混合型DG因为是多种电源组合叠加，所以波动性由叠加的电源类型所决定。综上可知，DG随机性会影响LSC波动，随机性越强，波动幅度越大，但LSC分布特征仍与负荷分布特性保持一致。

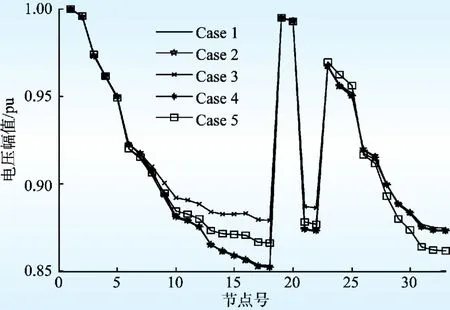
图4 各情景下达到LSC时节点电压均值图Fig.4 Node voltage amplitude mean of LSC in different scenarios

图4给出了各情景下LSC时节点电压的均值分布。比较图4和表4中Case 2、Case 3的结果可知，在7、16这2个节点中，DG接入节点16时效果更明显，这是因为配电网一般为辐射型线路，越到馈线末端，其电压降越大，越难满足电压约束条件，而DG能有效稳定和提升接入点电压。图4所示Case 3和Case 5的10～18节点电压提升较明显，也说明DG安装在电压降较大处合适。

当负荷增长超过一定极限后，配电网不能继续承担增长的需求，则需找出其制约因素，重新规划和改造。表5列出了各情景下LSC时的典型支路功率，除出口馈线支路(1-2，2-3)功率将达到约束功率外，其他典型支路功率裕度均宽松，所以只需升级出口馈线容量就能达到增大供电能力的效果。如将出口馈线(支路1-2，2-3)容量更换成8 MVA，在Case 5下LSC均值约为7 286.4 kW，较之前提升了3.0%，提升范围不大，即使将全部支路容量升至8 MVA，Case 5下均值约为7 348.1 kW，提升也仅3.9%，因此此时影响LSC的最大因素还是节点电压约束，图4可以看出馈线中末端节点电压明显低于前端，说明该配电网的薄弱在于中末端节点电压降上，需要在电压较低的节点处增加调压装置或无功自动补偿装置来提高电压的大小，以此来提升配电网最大供电能力，同时对于节点电压的稳定也起到关键作用。

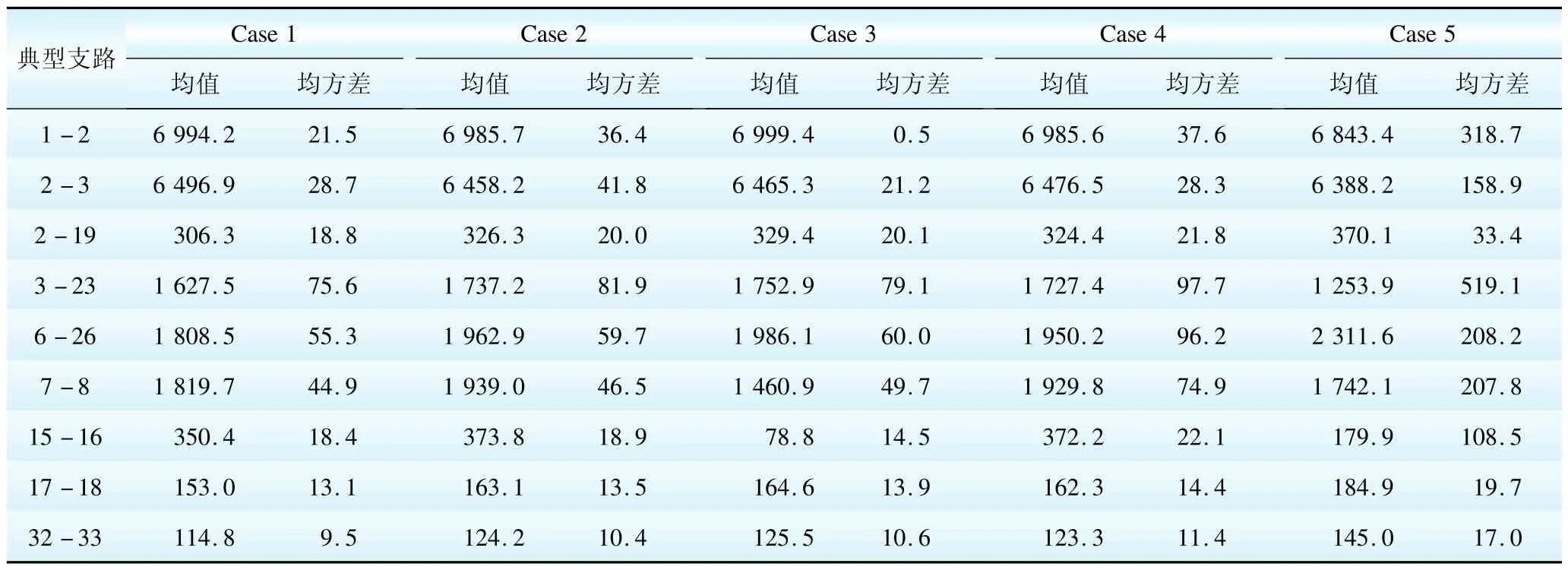
表5 各情景下达到LSC时典型支路视在功率Table 5 Typical branch power of LSC in different scenarios(apparent power)kVA

4 结 论

(1)DG接入配电网可提升网络静态安全裕度，增强现有网络结构对主网电力的消纳吸收作用。

(2)DG和负荷的随机性分布特性影响LSC分布，DG随机性越强，LSC波动幅度越大，且LSC近似服从正态分布，在接入配电负荷时应考虑负荷时变性与LSC分布特性相统一的原则。

(3)限制LSC提升的关键点在于负荷节点的电压降约束，在电压较低的节点处增加调压装置或无功自动补偿装置可提高节点处电压大小及起到稳定电压的作用，进而提升LSC。

[1]陈浩.配电网供电能力的计算方法研究[D].上海:上海交通大学，2009.

[2]王成山，罗凤章，肖峻，等.基于主变互联关系的配电系统供电能力计算方法[J].中国电机工程学报，2009，29(13):86-91.

Wang Chengshan，Luo Fengzhang，Xiao Jun，et al.An evaluation method for power supply capability of distribution system based on analyzing interconnections of main transformers[J].Proceedings of the CSEE，2009，29(13):86-91.

[3]肖峻，张婷，张跃，等.基于最大供电能力的配电网规划理念与方法[J].中国电机工程学报，2013，33(10):106-113.

Xiao Jun，Zhang Ting，Zhang Yue，et al.TSC-based planning idea and method for distribution networks[J].Proceeding of the CSEE，2013，33(10):106-113.

[4]肖峻，谷文卓，郭晓丹，等.配电系统供电能力模型[J].电力系统自动化，2011，35(24):47-52.

Xiao Jun，Gu Wenzhuo，Guo Xiaodan，et al.A supply capability model for distribution system[J].Automation of Electric Power System，2011，35(24):47-52.

[5]谷文卓.配电网最大供电能力的定义、模型与计算方法[D].天津:天津大学，2012.

[6]郭晓丹.配电网最大供电能力的性质与影响因素[D].天津:天津大学，2012.

[7]Li Shenghu，Ding Ming，Du Shaowu.Transmission loadability with field current control under voltage depression[J].IEEE Transactions on Power Delivery，2009，24(4):2142-2149.

[8]Diaz G.Maximumloadabilityofdroopregulatedmicrogridsformulation and analysis[J].IET Generation，Transmission＆Distribution，2013，7(2):175-182.

[9]Michael E K，Nicholas G M，Costas D V.Maximizing powersystemloadabilityinthepresenceofmultiplebinding complementarity constraints[J].IEEE Transactions on Circuits and Systems Society，2007，54(8):1775-1787.

[10]Wang Yanling，Han Xueshan，Zhou Xiaofeng，et al.Line loadability analysis including var supply capability and load voltage characteristics[C]//Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies. Nanjing:IEEE，2008:1132-1136.

[11]Lomi A，NguyenCH，MithulananthanN.Applicationof distributed generation to enhance loadability of distribution system，a case study[C]//2009 IEEE PES/IAS Conference on Sustainable Alternative Energy(SAE).Valencia:IEEE，2009:1-7.

[12]Nuri M，Miveh M R，Mirsaeidi S，et al.Distributed generationplacement to maximize the loadability of distribution system using geneticalgorithm[C]//Proceedingsof 17thConferenceon Electrical Power Distribution Networks(EPDC).Tehran:IEEE，2012:1-5.

[13]汪卫华.现有配电模式下配网供电能力研究[J].继电器，2007，35(14):13-16.

Wang Weihua.Research on supply capability of distribution network under present distribution mode[J].Relay，2007，35 (14):13-16.

[14]陈浩，张焰，俞国勤，等.配电网最大供电能力计算方法[J].中国电力，2009，42(8):20-23.

Chen Hao，Zhang Yan，Yu Guoqin，et al.A new algorithm to evaluate maximum load supplying capability of distribution network [J].Electric Power，2009，42(8):20-23.

[15]Fan Tianrong，ChenXingying，LiaoYingchen，etal.The maximum power supply capacity calculation based on the actual load characteristics[C]//TENCON 2013-2013 IEEE Region 10 Conference(31194).Xi’an:IEEE，2013:28-32.

[16]邱丽萍，范明天.城市电网最大供电能力评价算法[J].电网技术，2006，30(9):68-71.

Qiu Liping，Fan Mingtian.A new algorithm to evaluate maximum power supply capability of urban distribution netwrok[J].Power System Technology，2006，30(9):68-71.

[17]李振生.智能电网背景下含分布式电源配电网的最大供电能力研究[D].天津:天津大学，2013.

[18]王成山，郑海峰，谢莹华，等.计及分布式发电的配电系统随机潮流计算[J].电力系统自动化，2005，29(24):39-44.

Wang Chengshan，Zhen Haifeng，Xie Yinghua，et al.Probabilistic power flow containing distributed generation in distribution system [J].Automation of Electric Power System，2005，29(24):39-44.

[19]王敏.分布式电源的概率建模及其对电力系统的影响[D].合肥:合肥工业大学，2010.

[20]王守相，王成山.现代配电系统分析[M].北京:高等教育出版社，2007.

[21]段玉兵，龚宇雷，谭兴国，等.基于蒙特卡罗模拟的微电网随机潮流计算方法[J].电工技术学报，2011，26(1):274-278.

Duan Yubing，Gong Yulei，Tan Xingguo，et al.Probabilistic power flow calculation in microgrid based on monte-carlo simulation[J]. Transaction of China Electrotechnical Society，2011，26(1): 274-278.

[22]秦立军，马其燕.智能配电网及其关键技术[M].北京:中国电力出版社，2010.

Load Supplying Capability for Distribution Network Considering Distributed Generation Randomness

ZHANG Liming，QI Xianjun
(School of Electrical Engineering and Automation，Hefei University of Technology，Hefei 230009，China)

Distributed generation(DG)is more and more widely used and gradually connected to the distribution network，whose influence on the distribution network is significant.However，current calculation methods of load supplying capability (LSC)for distribution network do not consider the randomness effects of DG.To solve this problem，LSC model was proposed firstly.With considering the randomness of DG in the probabilistic power flow calculation of Monte Carlo simulation，the improved load factor method and the LSC approximation method with considering voltage and the branch power constraints were applied to calculate the LSC of distribution network.Then the IEEE-33 example of distribution network was used to validate the effectiveness of the proposed model and algorithm，and the LSC variations in different scenarios were simulated.Simulation results show that the DG connected to distribution network can promote the network static safety margin，and the randomness of DG affects the LSC distributed characteristics.Finally the weak link that restricted the LSC promotion was analyzed.It is suggested to add voltage regulator or automatic reactive compensator at low level voltage nodes.

distributed generation；randomness；load supplying capability；improved load factor method；voltage and branch power constraints

TM 76

A

1000-7229(2015)11-0038-07

10.3969/j.issn.1000-7229.2015.11.006

2015-09-16

2015-10-26

张李明(1989)，男，硕士研究生，研究方向为电力系统规划与可靠性；

(编辑：张媛媛)

国家自然科学基金项目(51007017)。

Project Supported by National Natural Science Foundation of China (51007017).

齐先军(1977)，男，博士，副教授，硕士生导师，研究方向为电力系统规划与可靠性、概率统计方法和人工智能在电力系统的应用等。