变电容载比与下一级中压配电网络关系的量化分析

肖峻，刘柔嘉，龙梦皓

(智能电网教育部重点实验室(天津大学)，天津市300072)

变电容载比与下一级中压配电网络关系的量化分析

肖峻，刘柔嘉，龙梦皓

(智能电网教育部重点实验室(天津大学)，天津市300072)

变电容载比是配电网规划的重要指标，现有导则指出，下级配电网络较强时容载比可取低，但未提供量化分析方法，为此提出了一种基于最大供电能力(total supply capability，TSC)的容载比与下级中压配电网络关系的量化分析方法。在同时考虑变电站内主变转带和下级网络转带的情况下，TSC理论能够计算一个配电网满足“N-1”安全准则条件下的最大负荷供应能力。研究了网络不同强弱时的容载比数据，并通过改变馈线容量、联络位置和联络规模来探究容载比与网络强弱的关系以及容载比的变化范围，得到了容载比取低的量化结论与推荐建议，丰富和发展了现有的规划导则。

配电网；导则；容载比；最大供电能力

0 引 言

配电网是城市的基础设施，对城市供电安全具有重大影响。中国经过十几年的城市电网建设，很多城市配电网得到了跨越式的发展，同时一些新的问题和挑战也逐步凸显出来。容载比是指变电容量与最高负荷之比，反映了容量备用情况，是影响电网规划的重要的指标。2006年修订颁布的国家电网公司《城市电网规划设计导则》指出，下级配电网较强时容载比可取低[1]，但未提供量化计算依据。如何衡量网络强弱以及对应的合理容载比范围，是规划工作中迫切需要解决的问题。

目前容载比的相关研究主要集中于容载比在变电站容量规划的应用、分区域计算容载比和多电压等级容载比等方面。文献[2-3]提出了基于单个变电站的容载比定义，并在此基础上对容载比各参数的合理取值进行了探讨。文献[4]提出把整个地区划分为若干个片区，分区计算变电容载比。文献[5]在综合考虑配电网容载比选取的技术性和经济性基础上，建立了求解多电压等级配电网最优容载比的模型以及离散粒子群优化算法。但是，现有研究均未解决下级网络较强时容载比如何取低这一问题。

最大供电能力(total supply capability，TSC)是指一定供电区域内配电网满足“N-1”安全准则[6]，并考虑实际运行约束条件下的最大负荷供应能力[7]，是反映配电系统安全与效率的关键指标。TSC同时计及了变电站内主变间和下级网络的负荷转移，因此本文利用TSC来解决容载比与下级网络的关系。

本文首先计算TSC，再根据主变容量与TSC计算配电网达到TSC时的容载比；然后在不改变主变容量的情况下，改变网络结构，通过对比研究容载比与网络强弱的量化关系。

1 基本概念

1.1 容载比的概念与选取原则

容载比是指某一供电区内变电设备总容量与供电区最大负荷之比[1]，反映了电网的容量备用情况，是反映电网供电能力的重要技术经济指标之一，也是宏观控制变电总容量和规划安排新增变电容量的依据。

由容载比的定义可知，当容载比取值增加时，在相同负荷水平下，变压器总容量将增加，导致电网建设投资增加，也会使电网运行成本增加，从而使电费增加，或使电网企业经济效益降低。因而容载比取值不宜过大。相反，若容载比取值减小，可能导致电网的适应性变差，使调度不够灵活，甚至发生卡脖子现象。因而，容载比取值也不宜过小。

规划导则指出，下级配电网较强时容载比可取低。同时，还明确规定了应加强和改善网络结构，使其既可满足供电可靠性要求又可降低容载比。并提出了降低容载比的措施，如变电所增加主变台数、次级电网增加转移负荷能力、提高功率因数、提高自动化程度等。

1.2 最大供电能力TSC的概念

1.2.1 TSC的定义

配电网供电能力定义为所有馈线“N-1”校验和变电站主变“N-1”校验均满足时，该配电网所能带的最大负荷。“N-1”校验时要考虑主变间和馈线间的负荷转带、网络中主变间以及馈线间的联络关系、主变和馈线的容量、主变过载系数等配电网实际运行约束。除了配电网总体TSC外，TSC模型和计算还给出达到TSC时各主变和馈线上的负荷分布情况。

1.2.2 基于馈线互联的TSC模型

采用基于馈线互联关系的模型[7]，能完整地计及馈线“N-1”和主变“N-1”故障，还能给出馈线负荷分布结果。

以满足馈线“N-1”和主变“N-1”校验作为约束条件，将配电网所带负荷最大作为目标函数，得到基于馈线互联的TSC模型如下[7]:

目标函数:

约束条件:

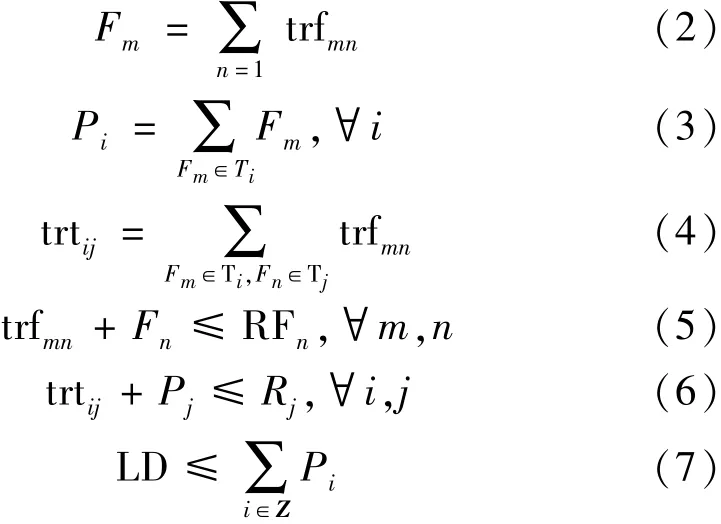
式中:Pi表示第i号主变所带的负荷；Fm表示第m号馈线所带的负荷；trfmn表示馈线m发生“N-1”时转带给馈线n的负荷量；trtij表示主变i发生“N-1”转带给主变j的负荷量；RFn表示馈线n的容量；Ri表示主变i额定容量；Ti表示主变i；Fm∈Ti表示馈线m出自主变i对应的母线；LD表示某个重载区负荷[8]的下限；Z为重载区所有主变的集合。

式(1)为目标函数，表示TSC为所有主变负荷之和的最大值；式(2)为馈线负荷分段等式约束，表示馈线m可能分为多段，其中每一段可转带给不同的馈线，所有转带出去的负荷之和等于该馈线的负荷；式(3)为主变-馈线负荷等式约束，表示主变i所带的负荷等于其母线上所有馈线负荷之和；式(4)为主变-馈线负荷转带等式约束，表示主变i发生“N-1”时转带给主变j的负荷是通过与2台主变相连馈线间的负荷转带完成的；式(5)为馈线“N-1”约束，表示馈线m发生“N-1”后，其负荷通过馈线联络转带给其他馈线，负荷转带后其他馈线不能过载；式(6)为主变“N-1”约束，表示主变j接受故障主变i转移负荷后长时间运行的负荷不超过其额定容量；式(7)为区域负载约束，含义是若存在某个区域负载很大，该区域内的主变负载之和大于给定负载LD，如有多个重载区，则增加不等式。

上述模型可利用文献[8]方法进行变形后采用线性规划软件(如Lingo)来求解即可得到TSC。

2 容载比与下级电网关系研究方法

2.1 描述网络强弱的方法

网络强弱主要由2方面因素决定，联络规模和联络位置。联络规模是指联络数多少，联络规模不同一般会导致网络强弱不同；联络位置是指某条馈线与哪条或哪几条馈线构成联络关系，不同馈线间的联络又构成了不同主变间的联络关系，联络位置不同一般会导致网络强弱不同。

2.1.1 联络规模

定义1:联络度(CD)指网络中实际站间联络数与可能的最多站间联络数之比。计算公式为

式中:QF表示实际站间联络数；QFmax表示可能的最多站间联络数。

联络度取值范围为0～1，联络度可以作为衡量网络强弱的指标，当联络度为0时网络最弱，为1时网络最强。当只有站内联络，不存在站间联络时取值为0；当所有主变均两两互联，即达到全联络时取值为1。

2.1.2 联络位置

馈线联络位置是指某条馈线与哪条或哪几条馈线构成联络关系，不同馈线间的联络又构成了不同主变间的联络关系，联络位置不同一般会导致TSC不同。采用文献[9]定义的联络均衡度指标来描述不同联络位置带来的影响。

定义2:加权联络均衡度(BD)指各联络通道间联络线的数量与各联络通道两端主变的平均容量R-ij的匹配程度[9]。计算步骤如下:

(1)计算联络通道L两端主变的平均容量Rij:

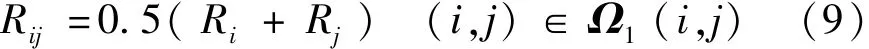
式中:Ri和Rj分别为主变Ti和Tj的容量；Ω1(i，j)为所有不同变电站的主变编号(i，j)两两组合的集合。

(2)计算联络基准度kij，联络通道Lij的联络基准度kij是在所有平均容量总和中所占的比例，即

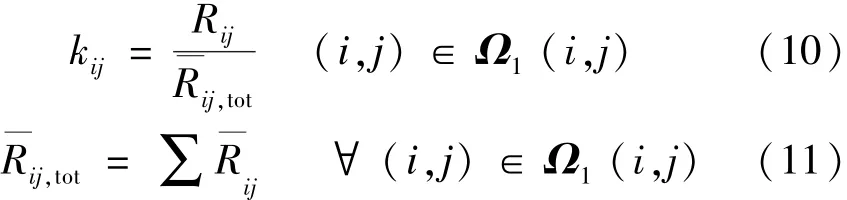
(3)计算联络基准差Dij，设M条联络线中，联络通道Lij内的联络线数量为Xij条，则有

(4)计算BD:

其中，Dsmax由主变容量、联络线规模和单台主变的最大馈线数决定，且Dsmax≥Ds。经上述公式计算，本文算例的Dsmax取值为2.8。BD的取值范围为[0，1)，当联络线分布非常均衡时BD趋近于1；当联络线分布十分不均衡时BD＝0。

2.2 基于TSC的容载比取值

本文提出利用TSC来确定容载比，首先计算TSC，然后以TSC对应的负荷为最大负荷来计算容载比，如下所示:

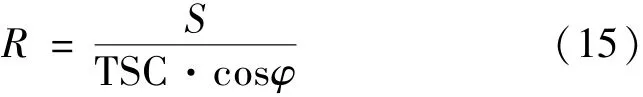
式中:R为容载比(MVA/MW)；S为变电容量(MVA)；cosφ为功率因数。

由式(15)可知，在变电容量不变的条件下，容载比与TSC成反比关系。当TSC最大时，容载比最小；当TSC最小时，容载比最大。所以，求出TSC的最大值、最小值便可得到变电容载比的变化范围。当所有主变两两互联，即系统达到全联络且联络容量足够大时，TSC是不增加变电容量可扩展到的最大TSC，称为全联络供电能力(maximum supply capability，MSC)[10]，此时容载比取得最小值；当只有站内联络，无任何站间联络时，TSC最小，称为变电站供电能力(substation supply capability，SSC)[10]，此时容载比取得最大值。

2.3 基于TSC的容载比研究方案

下面利用2.1、2.2节所述内容，设计研究步骤如图1所示。

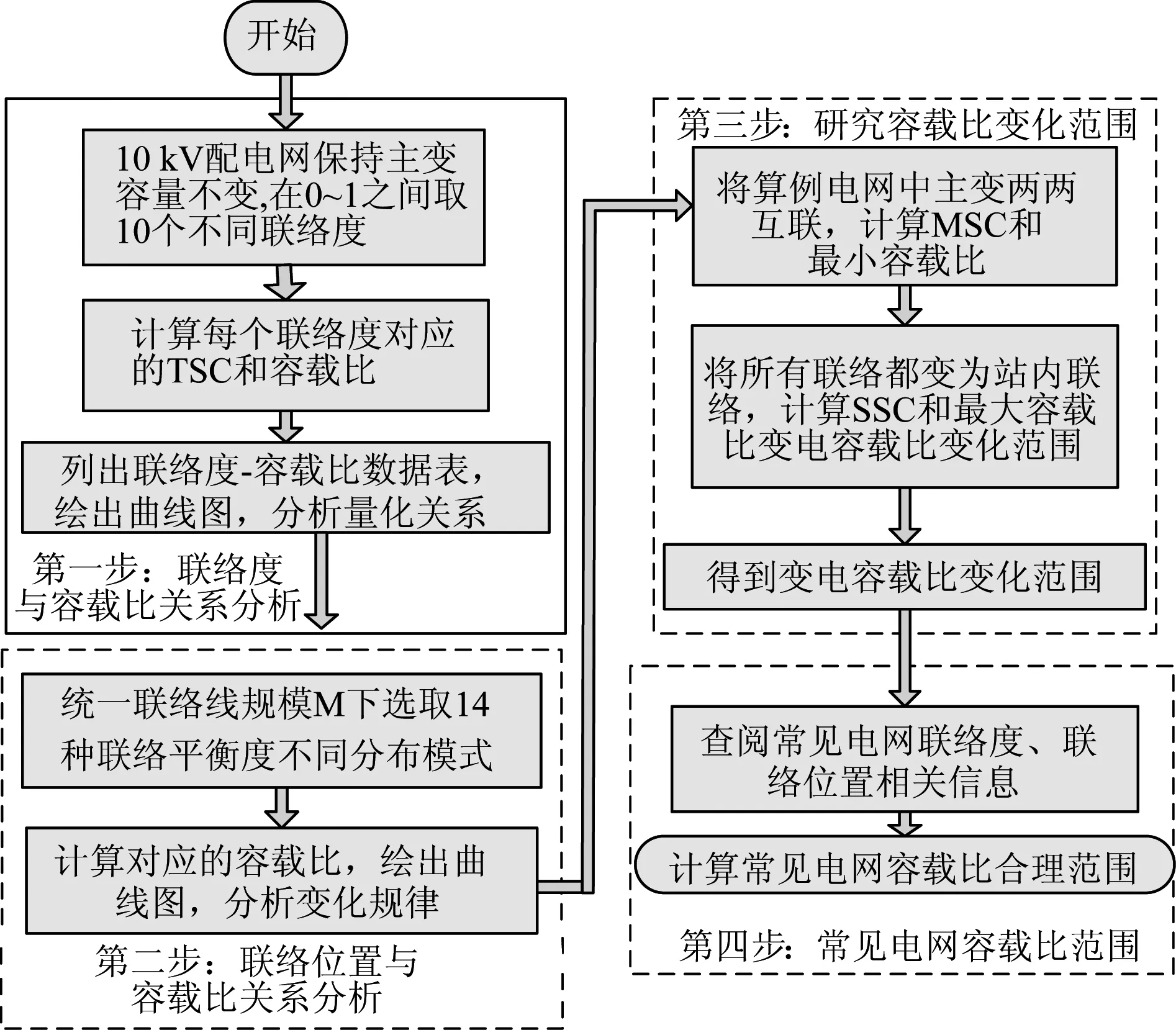
图1 容载比研究流程图Fig.1 Flowchart of capacity-to-load ratio research

3 研究结果

3.1 联络度与容载比的关系

变电站主变间的联络是影响TSC的重要因素，根据联络位置的不同，可将联络分为同一站内2台主变的站内联络和不同站2台主变的站间联络[11]。如图2所示，算例电网共3座110 kV变电站，6台主变和30回出线。变电站总容量为286 MVA，各馈线容量均为11.3 MVA，功率因数为0.95。其联络度为13/21＝0.62。

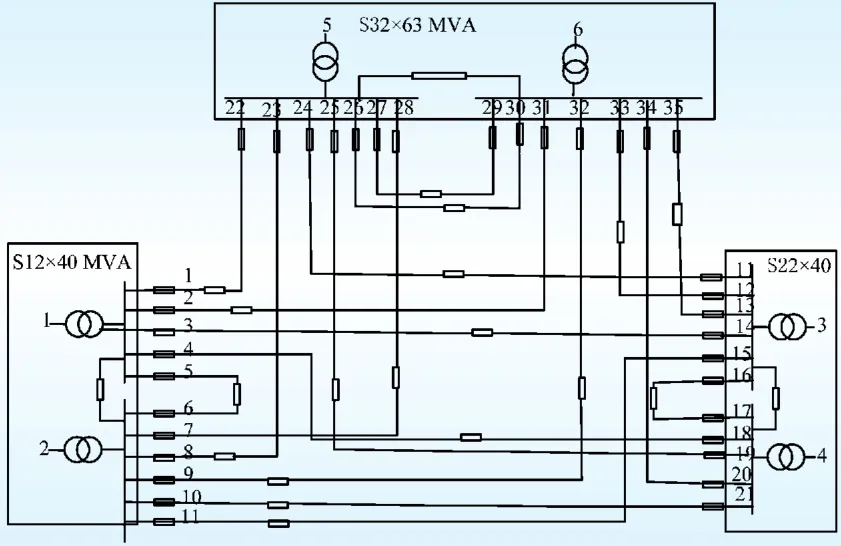
图2 算例配电网联络结构Fig.2 Illustration of test system

在保持主变容量不变的基础上，在0～1之间改变联络度，并对每个联络度对应的网络采用式(1)～(7)建立模型，利用文献[8]的方法进行变形后，用Lingo计算得到TSC，根据式(15)计算得到容载比，如图3所示。

图3 容载比与联络度关系Fig.3 Relationship between capacity-to-load ratio and CD

由图3可知，容载比与联络度近似为线性反比关系。联络度越大，即网络越强时，容载比越低；反之，联络度越小，即网络较弱时，容载比越高。

3.2 联络位置与容载比的关系

加权联络均衡度BD可以描述联络位置对容载比的影响。采用图2算例基本参数，在同一联络线规模M下选取14种BD不同的联络线分布模式，分别计算容载比和BD，得到容载比随BD变化的规律，其中M＝6的情况如图4所示。

图4 容载比与加权联络平衡度关系Fig.4 Relationship between capacity-to-load ratio and BD

由图4可知，在同一联络线规模M下，若BD达到最大值则容载比一定也达到最小值。结果表明BD大于0.7时容载比较小。整条曲线也存在着BD较小但容载比也达到最小值的点，称之为“尖点”。分析表明，当M较小时，若联络通道呈环形且无交叉联络时，容易出现“尖点”[12]。本文着重于找到使容载比最小的联络线分布情况，故不必苛求容载比与BD完全正相关。由规划原则和实践经验可知，容量大的主变应出更多的馈线，形成联络数量较多；容量小的主变出馈线相对较少，形成联络数量也较少。上述规律与规划原则和实践经验是一致的。

3.3 配电网变电容载比变化范围

TSC最大时，容载比最小，反之最大。所以求出TSC最大值、最小值便可得到变电容载比范围。当全联络时，联络度为1，此时TSC最大，称为MSC，对应的容载比最小；当只有站内联络，不存在站间联络，联络度为0时，TSC最小，称为SSC，容载比最大。

对于图2算例，馈线容量均为11.3 MVA，总主变容量为286 MVA，采用式(1)～(7)建立模型，利用文献[8]的方法进行变形后，经Lingo计算得到MSC为244 MVA，容载比为1.1；SSC为143 MVA，容载比为2.0；即该中压配电网变电容载比变化范围为1.1～2.0。

为验证该容载比变化范围的普遍性，另计算了其他算例，例如4座110 kV变电站，8台主变、总容量为412 MVA、76条出线的算例。由上述算法，经Lingo计算得到MSC为340 MVA，SSC为206 MVA，容载比变化范围为1.2～2.0，与前文算例得到的范围基本吻合。因此可以得出结论:达到TSC时配电网容载比的理论范围为1.1～2.0。

3.4 城市配电网容载比的一般取值范围

上述容载比理论计算范围太宽，操作性不好，以下试图根据我国配电网规划的实际情况得到更具操作性的容载比范围。

我国常见的城市配电网大多采用两联络和三联络接线模式，具有较多联络的电缆网在实际运行中一般也采用2～3个联络进行负荷转移。变电站间一般在地理上邻接的3～4个变电站相互联络，而很少跨区联络[13]。

图5为一个典型的城市配电网联络结构，联络线分布较均衡，经计算，其联络度CD为11/21＝0.5。

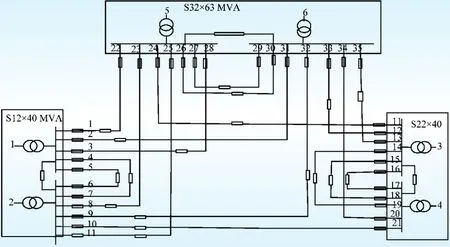
图5 典型城市配电网联络结构Fig.5 Illustration of common network

经查阅有关配电网接线模式以及组网供电模型的论文[14]以及多个实际配电网接线资料[15-17]，常见配电网的联络度CD为0.4～0.5，在联络线分布较均衡情况下，加权联络均衡度BD在0.6左右，依据图4规律，容载比为1.5～1.6，比目前导则的1.8～2.0有明显降低，即可多消纳负荷12%～33%。

4 结 论

(1)用联络度CD表示网络联络程度，发现达到TSC时的容载比与联络度近似呈线性反比关系，即CD越大容载比越低。

(2)CD为1时达到全联络，容载比取最小值；CD为0时，只有站内联络无站外联络，容载比取最大值。配电网容载比的理论范围为1.1～2.0；对于常见的城市配电网，容载比为1.5～1.6。

(3)用联络均衡度BD作为衡量联络位置的指标，研究发现同等联络规模下，BD越大，容载比取值更小。BD达到0.7以上时，容载比可达到1.5以下。此时，站间联络相对站内联络的比例应达到1∶1。

综上，在目前互联程度较高的城市配电网中，可突破导则中容载比2.0左右的限制，根据本文研究结果并考虑适当裕度，建议规划配电网的容载比控制在1.6左右，可以多消纳负荷约20%。还需指出，本文结论是针对2主变变电站配电网得到，对于三主变的情况采用本文方法不难得到相应结果。另外，对于负荷快速增长区域的容载比仍然可维持在约2.0的较高水平。

[1]国家电网公司.城市电力网规划设计导则[Z].2006.

[2]赵俊光，王主丁.电网规划中对变电容载比的探讨[J].电力建设，2008，29(6):12-14.

Zhao Junguang，Wang Zhuding.Discussion on the change of the load ratio of the capacitor in power network planning[J].Electric Power Construction，2008，29(6):12-14.

[3]李永伟.容载比在电网规划中的重要性[J].沿海企业与科技，2009(3):32-33，31.

Li Yongwei.The importance of capacity load ratio in power system planning[J].Coastal Enterprises and Science＆Technology，2009 (3):32-33，31.

[4]李欣然，刘友强，朱湘友，等.地区中压配电网容载比的研究[J]继电器，2006，34(7):47-50.

Li Xinran，Liu Youqiang，Zhu Xiangyou，et al.Study on capacity load ratio of medium voltage distribution network[J].Relay，2006，34(7):47-50.

[5]陈浩，张焰，俞国勤，等.多电压等级配电网最优容载比的计算方法[J].电气应用，2011(1):25-29.

Chen Hao，Zhang Yan，Yu Guoqin，et al.Multi voltage distribution network optimumcapacityloadratiocalculationmethod[J]. Electrotechnical Application，2011(1):25-29.

[6]肖峻，贡晓旭，王成山.配电网最大供电能力与N-1安全校验的对比验证[J].电力系统自动化，2012，36(18):86-90

Xiao Jun，Gong Xiaoxu，Wang Chenshan.Comparative research between TSC and N-1 security verification for distribution networks [J].Automation of Electric Power Systems.2012，36(18):86-90.

[7]肖峻，谷文卓，王成山，等.基于馈线互联关系的配电系统供电能力计算方法[J].电力系统自动化，2013，35(17):72-77.

Xiao Jun，Gu Wenzhuo，Wang Chengshan，et al.An evaluation method for power supply capability of distribution system based on analyzing interconnections of feeder[J].Automation of Electric Power Systems，2013，35(17):72-77.

[8]肖峻，谷文卓，郭晓丹，等.配电系统供电能力模型[J].电力系统自动化，2011，35(24):47-52.

Xiao Jun，Gu Wenzhuo，Guo Xiaodan，et al.Total supply capability model for distribution systems[J].Automation of Electric Power Systems，2011，35(24):47-52.

[9]肖峻，祖国强，贺琪博，等.馈线联络对配电网最大供电能力的作用机理[J].电力系统自动化，2015，39(8):38-44.

Xiao Jun，Zu Guoqiang，He Qibo，et al.Mechanism of the maximum power supply capacity of the feeder[J].Automation of Electric Power Systems，2015，39(8):38-44.

[10]肖峻，张婷，张跃，等.基于最大供电能力的配电网规划理念与方法[J].中国电机工程学报，2013，33(10):106-113.

Xiao Jun，Zhang Ting，Zhang Yue，et al.Concept and method of distribution network planning based on maximum power supply capacity[J].Proceedings of the CSEE，2013，33(10):106-113.

[11]Luo F Z，Wang C S，Xiao J，et al.Rapid evaluation method for power supply capability of urban distribution system based on N-1 contingency analysis of main-transformers[J].International Journal ofElectricalPowerandEnergySystem，2010，32(10): 1063-1068.

[12]葛少云，韩俊，刘洪，等.基于供电能力的主变站间联络结构优化[J].电网技术，2012，36(8):131-135.

Ge Shaoyun，Han Jun，Liu Hong，et al.Optimization of contact structure among main transformer stations in regional power network based on power supply capability[J].Power System Technology，2012，36(8):131-135.

[13]葛少云，何文涛，刘洪，等.中压配电系统供电模型综合评价[J].电力系统保护与控制，2012，40(13):104-109.

Ge Shaoyun，Han Jun，Liu Hong，et al.Comprehensive evaluation of power supply model for medium voltage distribution system[J]. Power System Protection and control，2012，40(13):104-109.

[14]陈庭记，程浩忠，何明，等.城市中压配电网接线模式研究[J].电网技术，2000，36(9):131-135.

Cheng Tingji，Cheng Haozhong，He Ming，et al.Research on the connection mode of urban middle voltage distribution network[J]. Power System Technology，2000，36(9):131-135.

[15]黑龙江齐齐哈尔电业局.齐齐哈尔市城区10 kV配电网“十一五”发展规划及2020年远景目标展望[Z].2007:26-30.

[16]王凯军，肖峻，葛少云，等.杭州滨江区10 kV配电网规划中的接线模式与转供能力分析[J].中国电力，2005，38(2):64-69.

Wang Kaijun，Xiao Jun，Ge Shaoyun，et al.Connection mode and transfer capability analysis of 10 kV distribution network planning in Binjiang District，Hangzhou[J].Electric Power，2005，38(2): 64-69.

[17]刘宇，赵咏梅.德阳城区10 kV配电网规划研究[J].华中电力，2009，22(4):40-43.

Liu Yu，Zhao Yongmei.Research on 10 kV distribution network planning in Deyang[J].Central China Electric Power，2009，22 (4):40-43.

(编辑：张小飞)

Quantitative Analysis of Relationship between Substation
Capacity-to-Load and Subordinate Medium Voltage Distribution Network

XIAO Jun，LIU Roujia，LONG Menghao
(Key Laboratory of Smart Grid of Ministry of Education，Tianjin University，Tianjin 300072，China)

Substation capacity-to-load ratio is an important index of distribution network planning，and existing guideline indicates that capacity-to-load ratio can be lower when subordinate distribution network is strong；however，there are no quantitative analysis methods.This paper proposed a quantitative analysis method for the relationship between capacity-toload ratio and subordinate medium voltage distribution network based on the total supply capability(TSC)theory.TSC theory can be used to calculate the maximum load supply capacity of a distribution network under the condition of meeting the“N-1”security criteria，with taking the substation transformer transfer in transformer substation and the subordinate network transfer into account.This paper analyzed the capacity-to-load ratio data with different network strength，and explored the relationship between capacity-to-load ratio and network strength，as well as the range of capacity-to-load ratio through changing feeder capacity，connection location and scale.Finally，the quantitative conclusion of lower capacity-toload ratio and its recommendations were proposed，which could enrich and develop the existing planning guidelines.

distribution network；guideline；capacity-to-load ratio；total supply capability(TSC)

TM 714

A

1000-7229(2015)11-0045-06

10.3969/j.issn.1000-7229.2015.11.007

2015-06-30

2015-09-20

肖峻(1971)，男，博士，教授，主要从事配系统规划、微网规划设计的研究和应用工作；

刘柔嘉(1994)，女，本科，主要研究方向为配电网最大供电能力；

龙梦皓(1992)，男，硕士，主要从事电网安全域、智能电网方面的研究。

国家自然科学基金项目(51277129)。

Project supported by National Natural Science Foundation of China (51277129).