一种修正下降的非线性共轭梯度法
张小让,朱志斌,邢明燕
一种修正下降的非线性共轭梯度法
张小让,朱志斌,邢明燕
(桂林电子科技大学数学与计算科学学院,广西桂林 541004)
为求解无约束优化问题,基于MMHS方法和DY方法,提出了一种修正下降的非线性共轭梯度法。在Armijo线搜索下,该算法是全局收敛的。数值实验证明了该算法的有效性和可行性。
无约束优化;共轭梯度法;Armijo线搜索;全局收敛性
令f:Rn→R连续可微,并考虑如下无约束优化问题:
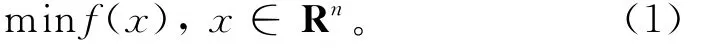
用共轭梯度法[1]求解问题(1),迭代步为:

其中:αk(αk≥0)为步长,由一定的线搜索决定;dk为搜索方向,满足(g(x))Tdk<0。并定义:
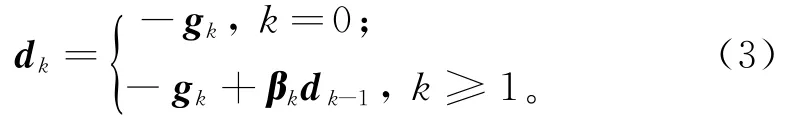
其中βk为参数。MHS[2]方法和DY[3]方法是2个熟悉的共轭梯度法,其参数βk定义为:
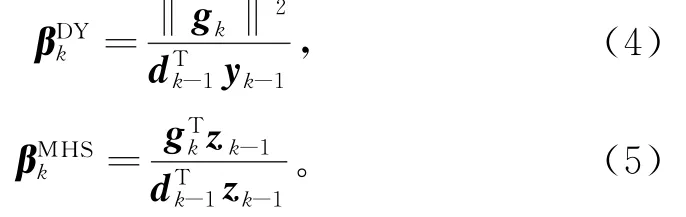
其中:gk=g(xk);g(x)=▽f(x);yk-1=gk-gk-1;sk=xk+1-xk;‖•‖为欧几里得范数。另外,Armijo线搜索[4]是普遍采用的精确线搜索,给定δ∈(0, 1),ρ∈(0,1),并令
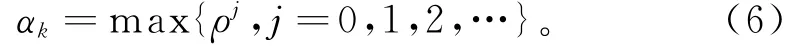
满足线搜索条件:

易知,若采用Armijo精确线搜索,可得到一个下降方向。为此,构建一个新的共轭梯度法,证明在Armijo线搜索下算法的全局收敛性。
1 修正的非线性共轭梯度法
文献[5]对MFR方法[6-8]和MPRP方法[6-10]进行处理,给出了一种由DY和MMHS[2]所构造的共轭梯度法,称为修正的非线性共轭梯度法(简称DYMMHS方法)。用此共轭梯度法解决问题(1),在DY方法和MMHS方法中,搜索方向dk分别为:
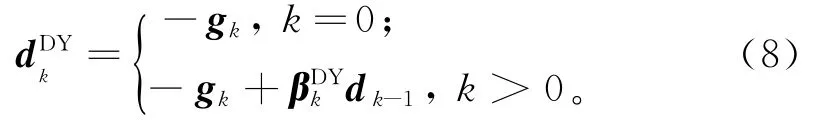
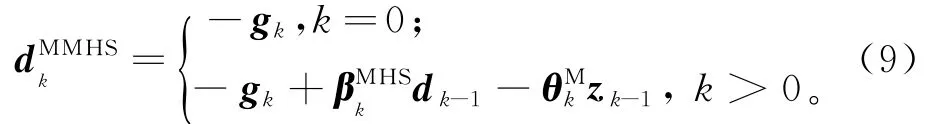
其中:

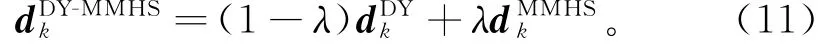
基于式(11),给出一种共轭梯度法,并称为DYMMHS方法。
算法1(DY-MMHS方法) 给定常数δ,λ∈(0,1),ρ∈(0,1),ε>0,选择一个初始点x0∈Rn,并令k∶=0。
1)通过式(11)计算dk,当‖gk‖<ε时,中止。
2)用Armijo精确线搜索计算步长αk。
3)令xk+1=xk+αkdk。
4)令k∶=k+1,并返回步骤1)。
DY-MMHS方法可产生目标函数的充分下降方向,此性质独立于线搜索,且算法具有二次终止性。
2 收敛性分析
通过分析算法的全局收敛性,做出如下基本假设[]。
假设1 1)水平集W={x∈Rnf(x)≤f(x0)}有界。
2)存在W的某个邻域N,使得f在该邻域上连续可微,且导数满足Lipschitz条件,即存在常数L>0,使得
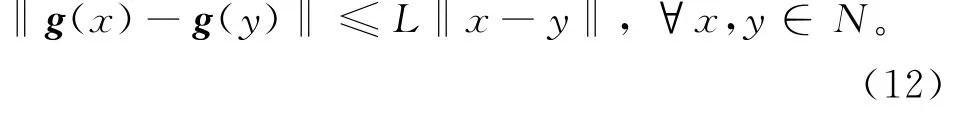
由假设1易得该算法收敛性定理。
定理1 设假设1成立,{xk}由DY-MMHS方法产生,则有
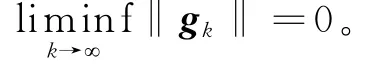
证明(反证法) 假设结论不成立,则存在常数ε>0,使得‖gk‖≥ε,∀k。
由Armijo线搜索及假设1可得
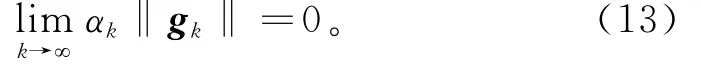

另由Armijo线搜索,对充分大的k∈K,有
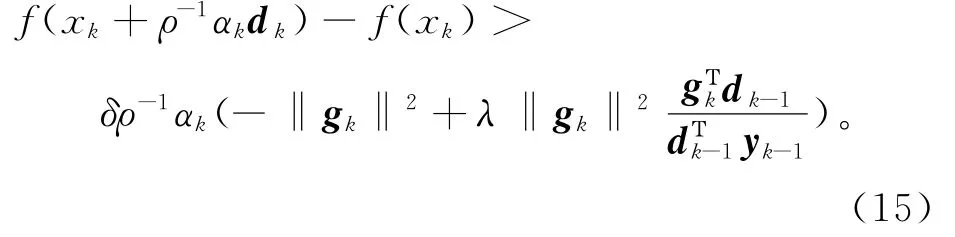
结合微积分中值定理及Lipschitz条件(12),存在tk∈(0,1),使得
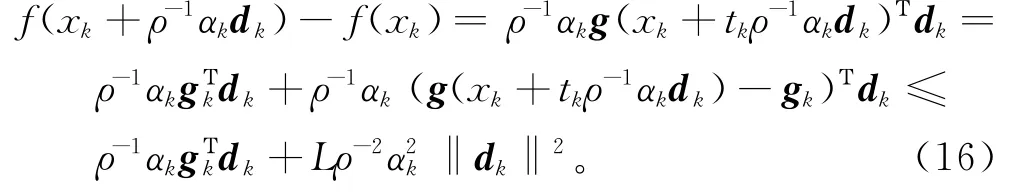
其中,L>0为梯度g的Lipschitz常数。因此,对于充分大的k∈K,有
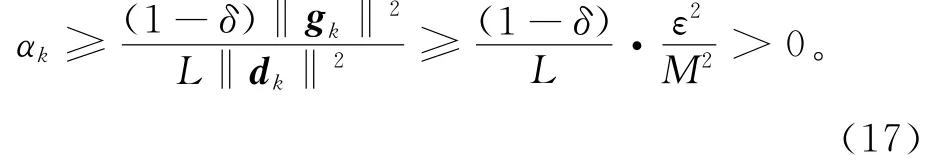
这与式(14)矛盾,因此假设不成立,故结论成立。证毕。
以上结果表明,DY-MMHS方法在Armijo线搜索下是全局收敛的。
3 数值实验
通过Matlab编程进行数值实验以验证MMHSDY算法的有效性和稳定性。运行环境为Windows 7,Intel Pentium,内存2 GB,CPU 2.50 GHz,测试环境为Matlab v8.1(R2013a)。x0为初始点,xk为末点。数值实验的算例为:
例1 f(x)=(x1-2)2+0.04/(-x21/4-x22+ 1)+(x1-2x2+1)2/0.2+(x2-1)2,x0=(1,1), xk=(1.795 4,1.377 9)。
例2 f(x)=4(x1-5)2+(x2-6)2,x0=(1, 1),xk=(5.000 0,6.000 0)。
例3 f(x)=(1.5-x1(1-x2))2+(2.25-x1(1-x22))2+(2.625-x1(1-x32))2,x0=(1,1), xk=(3.000 0,0.500 0)。
例4 f(x)=(x2-x21)2+(1-x1)2,x0= (-1.2,1),xk=(1,1)。
例5 f(x)=(x21+x2-11)2+(x1+x22-7)2, x0=(1,1),xk=(3.000 0,2.000 0)。
例6 f(x)=(x2-x21)2+100(1-x1)2,x0= (-1.2,1),xk=(1,1)。
令参数δ=0.001,ρ=0.5,λ=0.1。对于测试问题,‖gk‖为DY-MMHS算法的梯度范数,k为迭代步。终止条件为‖gk‖≤10-6。表1为DYMMHS算法实验结果,从表1可看出,对于所有算例,算法效果很好,其结果也很精确,同时消耗的时间也很少。
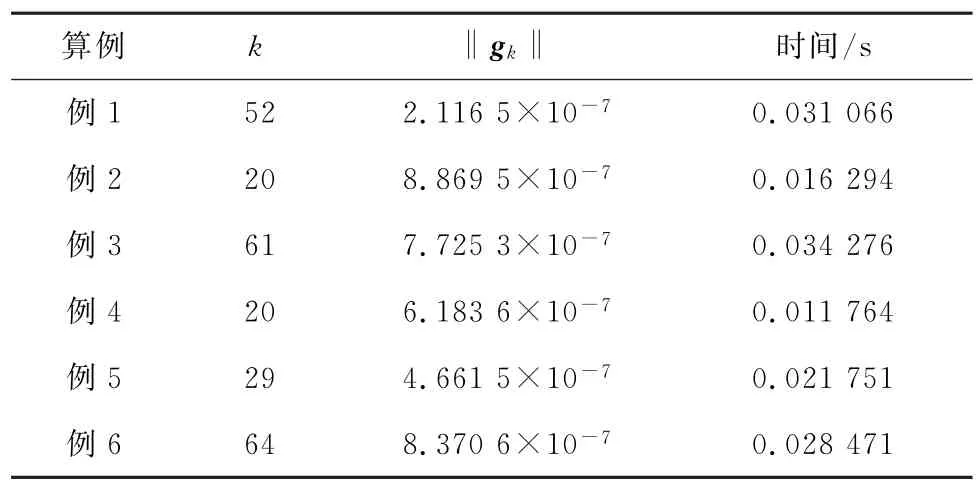
表1 DY-MMHS算法实验结果Tab.1 The numerical results of DY-MMHS method
4 结束语
在传统共轭梯度法基础上,将DY方法和MMHS方法结合在一起,寻求一种新的共轭梯度法,从而达到预想的结果。该算法的灵感来源于文献[5],采用的是Armijo线搜索。实验结果表明,算法在一定的条件下是收敛的。
[1] 袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,2007:183-199.
[2] 张丽.求解最优化问题的非线性共轭梯度法[D].长沙:湖南大学,2006:34-39.
[3] Dai Y H,Yuan Y.A nonlinear conjugate gradient method with a strong global convergence property[J].Siam Journal on Optimization,1999,10(1):177-182.
[4] 李董辉,童小娇,万中.数值最优化算法与理论[M].北京:科技出版社,2010:1-91.
[5] Tao Y.A class of descent nonlinear conjugate gradient methods[C]//2013 Fourth International Conference on Digital Manufacturing&Automation(ICDMA).IEEE Computer Society,2013:14-16.
[6] Polyak B T.The conjugate gradient method in extremal problems[J].Ussr Computational Mathematics& Mathematical Physics,1969,9(4):94-112.
[7] Fletcher R,Reeves C M.Function minimization by conjugate gradients[J].Computer Journal,1964,7(2):149-154.
[8] Polak E,Ribière G.Note sur la convergence de méthodes de directions conjuguées[J].Rev franaise Information recherche Opérationnelle,1969,(16):35-43.
[9] Zhang Li,Zhou Weijun,Li Donghui.Global convergence of a modified Fletcher-Reeves conjugate gradient method with Armijo-type line search[J].Numerische Mathematik,2006,104(4):561-572.
[10] Zhang Li,Zhou Weijun,Li Donghui.A descent modified Polak-Ribiere-Polyak conjugate gradient method and its global convergence[J].Ima Journal of Numerical Analysis,2006,26(4):629-640.
编辑:梁王欢
A modified descent nonlinear conjugate gradient method
Zhang Xiaorang,Zhu Zhibin,Xing Mingyan
(School of Mathematics and Computational Science,Guilin University of Electronic Technology,Guilin 541004,China)
To solve unconstrained optimization problem,based on DY method and MMHS method,a modified descent conjugate gradient method is presented.When Armijo line searching is used,the method is globally convergent.Numerical experiments show that the proposed method is effective and feasible.
unconstrained optimization;conjugate gradient method;Amijo line searching;global convergence
O224
A
1673-808X(2015)05-0424-03
2015-03-26
国家自然科学基金(11361018);广西自然科学基金(2014GXNSFFA118001);桂林市科学研究与技术开发计划(20140127-2)
朱志斌(1974-),男,湖南双峰人,教授,博士,研究方向为最优化理论与算法。E-mail:zhuzb@guet.edu.cn
张小让,朱志斌,邢明燕.一种修正下降的非线性共轭梯度法[J].桂林电子科技大学学报,2015,35(5):424-426.

