基于Gramian分解的对称半正定矩阵的正则化低秩逼近
张雪伟,江祝灵,段雪峰
基于Gramian分解的对称半正定矩阵的正则化低秩逼近
张雪伟,江祝灵,段雪峰
(桂林电子科技大学数学与计算科学学院,广西桂林 541004)
针对对称半正定矩阵的正则化低秩逼近问题,基于对称半正定矩阵的Gramian分解,将对称半正定矩阵的正则化低秩逼近问题转化为等价的无约束优化问题,并构造非线性共轭梯度方法求解转化后的无约束优化问题。数值实验验证了新方法的可行性。
对称半正定矩阵;正则化低秩逼近;非线性共轭梯度法;Gramian分解
记Rn×n为n×n实矩阵集合,SRn×n为n×n对称半正定矩阵集合,rank(B)和tr(B)分别为矩阵B的秩和迹。对于n×n阶矩阵B,设bi为矩阵B的第i列,则B可表示为B=(b1,b2,…,bn)。设[Bij]为矩阵B的第i行第j列元素,即[Bij]=bij。用vec(B)表示矩阵B的按列拉直向量,即vec(B)=(b1T,b2T,…,bnT)。‖B‖F表示矩阵B的F范数,则

研究对称半正定矩阵的正则化低秩逼近问题。
问题1 给定矩阵A,B,C∈Rn×n,正整数k≤n,参数0<α<1,求一个秩小于等于k的对称半正定矩阵¯X,使得
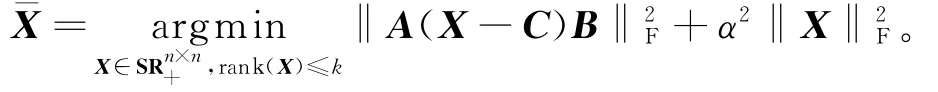
研究结构矩阵逼近问题采用的方法有低阶近似的截断奇异值分解法[1-2]、Lanczos双对角化过程[3]、Monte Carlo算法[4]。基于结构化总体最小二乘, Park等[5]提出Hankel低阶近似的数值方法,此方法后被用于Sylvester的低秩近似计算,并且在计算Sylvester逼近过程中给出了一元多项式的近似最大公约数[6-8]。Higham[9]和段雪峰[10]分别采用分半算法和共轭梯度法求解对称半正定矩阵的近似逼近; Suliman[11]采用交替投影算法和拟牛顿法求解Toeplitz矩阵逼近问题;唐鸣[12]采用牛顿法求解,将问题转化为无约束优化问题,但计算量较大,而且牛顿法对于大多数问题不是整体收敛,而改用拟牛顿法对Hankel矩阵逼近问题进行求解得到了较好的收敛效果。对称半正定矩阵的正则化低秩逼近问题几乎无人研究,原因在于难以刻画该问题的可行集。鉴于此,利用Gramian分解X=YYT,Y∈Rn×k,刻画该问题的可行集,将原问题转化为一个等价的无约束优化问题,应用带Armijo线性搜索的非线性共轭梯度法对等价问题求解。
1 主要结论
引理1 n×n阶对称半正定矩阵X的秩小于等于k,当且仅当存在矩阵Y∈Rn×k,使得X=YYT。
由引理1,问题1的可行集
Ω={X|X∈SRn×n+,ran k(X)≤k}
可刻画成X=YYT,Y∈Rn×k,因此,问题1可等价转化为问题2。
问题2 给定矩阵A,B,C∈Rn×n,参数α∈(0, 1),求一个n×k阶矩阵¯Y,使得
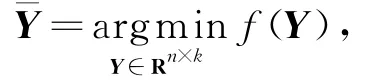
其中,
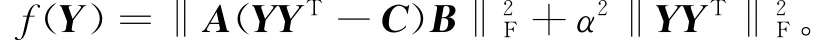
易知,若¯Y是问题2的解,则X=YY是问题1的解。问题2的搜索空间为nk,当k较小时,比问题1的搜索空间n2小很多。
定理1 目标函数f(Y)的梯度为:
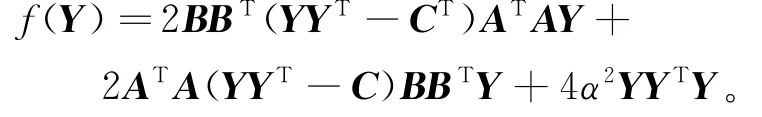
证明 由增量矩阵E∈Rn×k,有
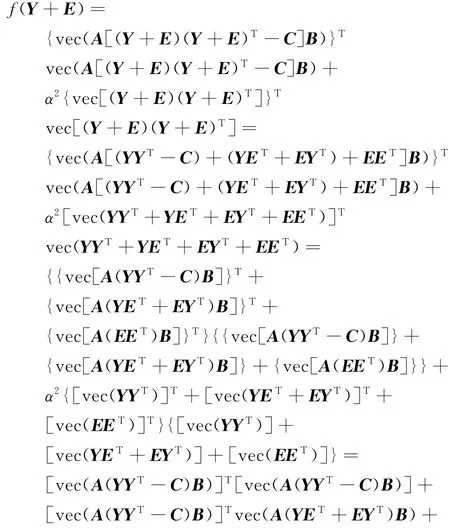
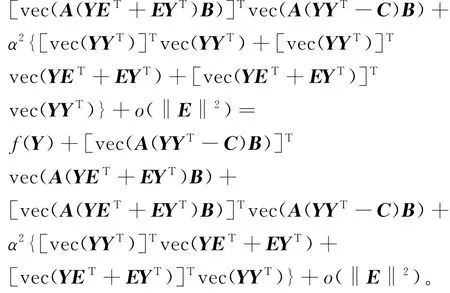
又由泰勒定理可知,
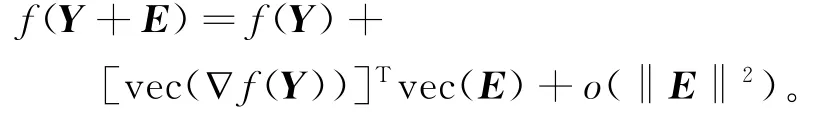
比较上述两式有
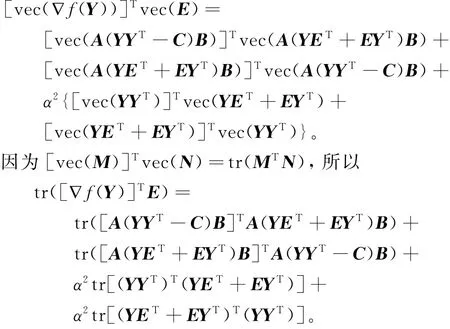
设E=eieTj,其中ei为n×n单位矩阵的第i列元素,ej为k×k单位矩阵的第j列元素,可得


证毕。
利用Armijo线搜索下的非线性共轭梯度方法求解问题2。
算法1(非线性共轭梯度算法) 1)初始化ρ∈(0,1),δ∈(0,0.5),σ∈(δ,0.5)。选取误差0≤t≪1,取初始值迭代矩阵Y0∈Rn×k,置k∶=0。
2)计算gk=▽f(Yk),若‖gk‖F<t,停机并输出≈Yk。
3)确定搜索方向dk,
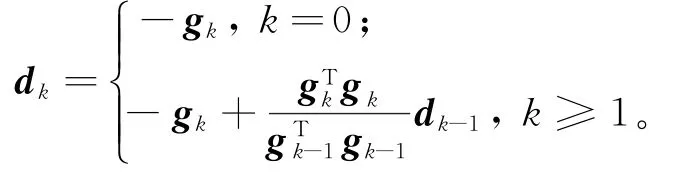
4)由Armijo线搜索方法确定搜索步长,即找一个最小的非负整数mk,使得

置αk=,ζk+1=ζk+αkdk。
5)令k∶=k+1,并转步骤2)。由文献[13]的定理,可建立算法1的收敛性定理。定理2 假设f连续可微且有界,若其梯度▽f是Lipschitz连续的,那么存在常数L>0,使得
‖▽f(X)-▽f(Y)‖F≤L‖X-Y‖F,∀X,Y∈Rn×k。那么由算法1生成的序列{Yk}满足

2 数值实验
实验在Matlab 2009a环境下运行,设▽fk=▽f(Yk),其中Yk是算法1中第k次迭代值,停机标准为‖▽fk‖<1×10-4。
例1 给定矩阵
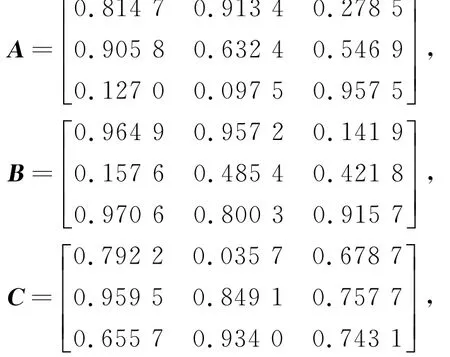
若k=1,α=0.3,初始值

用算法1求解。经过23次迭代,得到问题2的最优解

从而问题1的最优解为

其中rank(X*)=1,X*为对称半正定矩阵,其目标函数的梯度范数曲线如图1所示。
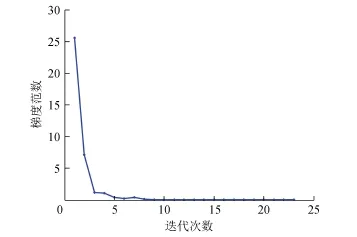
图1 n=3,k=1时的梯度范数曲线Fig.1 Gradient norm curve when n=3,k=1
例2 给定矩阵
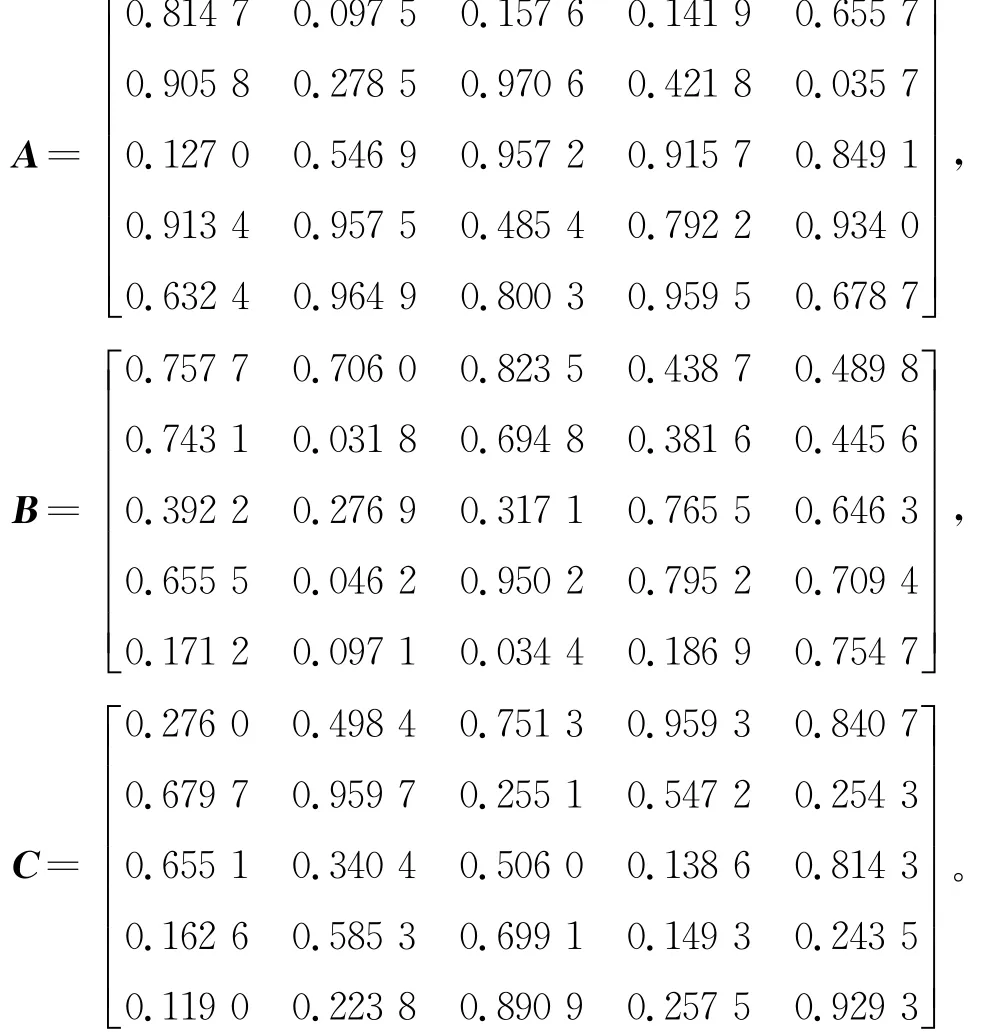
1)若k=2,α=0.3,初始值
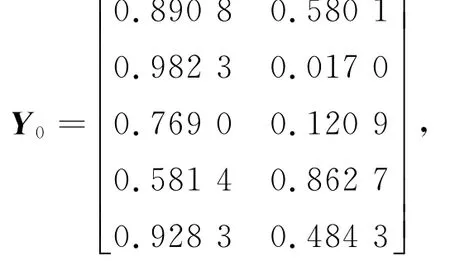
用算法1求解。经过280次迭代,得到问题2的最优解

从而问题1的最优解为

其中rank(X*)=2,X*为对称半正定矩阵,其目标函数的梯度范数曲线如图2所示。
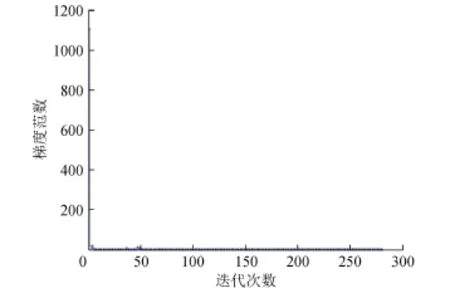
图2 n=5,k=2时的梯度范数曲线Fig.2 Gradient norm curve when n=5,k=2
2)若k=1,α=0.3,初始值

用算法1求解。经过75次迭代,得到问题2的最优解

从而问题1的最优解为
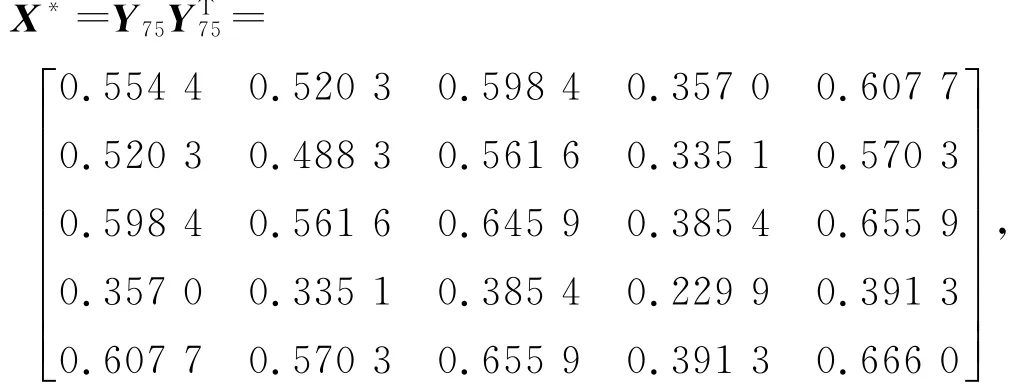
其中rank(X*)=1,X*为对称半正定矩阵,其目标函数的梯度范数曲线如图3所示。
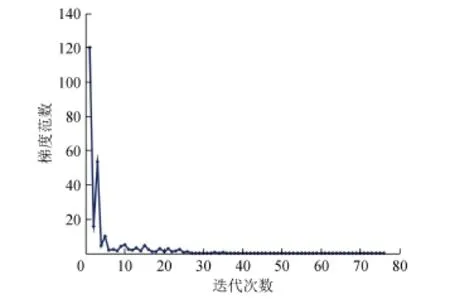
图3 n=5,k=1时的梯度范数曲线Fig.3 Gradient norm curve when n=5,k=1
3 结束语
利用Gramian分解X=YYT,Y∈Rn×k,刻画了问题1的可行集,将搜索空间维数降低,并把问题1转化为无约束优化问题2,通过Armijo线性搜索的非线性共轭梯度方法对问题2求解。在这个过程中,关键在于如何计算目标函数的梯度,用2个数值例子说明算法1的可行性。
[1] Golub G H,Van Loan C F.Matrix Computations[M]. Baltimore:Johns Hopkins University Press,1996:76-81.
[2] Hansen P C.The truncated SVD as a method for regularization[J].BIT Numerical Mathematics,1987,27: 534-553.
[3] Siman H D,Zha Hongyuan.Low rank matrix approximation using the Lanczos Bidiagonalization process withapplications[J].SIAM Journal on Scientific Computing, 2000,21:2257-2274.
[4] Drineas P,Kannan R,Mahoney M W.Fast Monte Carlo algorithms for matrices II:computing a low rank approximation to a matrix[J].SIAM Journal on Computing,2006,36:158-183.
[5] Park H,Zhang Lei,Rosen J B.Low rank approximation of a Hankel matrix by structured total norm[J].BIT Numerical Mathematics,1999,39:757-779.
[6] Li Bingyu,Yang Zhengfeng,Zhi Lihong.Fast low rank approximation of a Sylvester matrix by structured total least norm[J].Japan Society for Symbolic and Algebraic Computation,2005,11:165-174.
[7] Winkler J,Allan J.Structured low rank approximations of the Sylvester resultant matrix for approximate gcds of bernstein basis polynomials[J].Electronic Transactions on Numerical Analysis,2008,31:141-155.
[8] Winkler J,Allan J.Structured total least norm and approximate gcds of inexact polynomials[J].Journal of Computational and Applied Mathematics,2008,215:1-13.
[9] Higham N J.Computing a nearest symmetric positive semi-definite matrix[J].Linear Algebra and its Applications,1988,103:103-118.
[10] Duan Xuefeng,Li Jiaofeng,Wang Qingwen,et al.Low rank approximation of the symmetric positive semidefinite matrix[J].Journal of Computational and Applied Mathematics,2014,260:236-243.
[11] Al-Homidan S.Toeplitz matrix approximation[J]. Mathematical Sciences Research Journal,2002,2:104-111.
[12] 唐鸣.低秩Hankel矩阵逼近及其加权逼近的算法[D].南京:南京航空航天大学,2006:7-33.
[13] 李董辉,童小娇,万中.数值最优化算法与理论[M].北京:科学出版社,2005:75-81.
编辑:翁史振
Regularized low rank approximation of symmetric positive semi-definite matrix based on Gramian decomposition
Zhang Xuewei,Jiang Zhuling,Duan Xuefeng
(School of Mathematics and Computational Science,Guilin University of Electronic Technology,Guilin 541004,China)
The regularized low rank approximation of symmetric positive semi-definite matrix is studied.Based on Gramian decomposition of a symmetric positive semi-definite matrix,the regularized low rank approximation of the symmetric positive semi-definite matrix problem is transformed into an equivalent unconstrained optimization problem,and the nonlinear conjugate gradient method is constructed to solve the equivalent unconstrained optimization problem.The numerical experiments verify that the new method is feasible.
symmetric positive semi-definite matrix;regularized low rank approximation;nonlinear conjugate gradient method;Gramian decomposition
O241.6
A
1673-808X(2015)05-0419-05
2015-04-22
国家自然科学基金(11101100);广西自然科学基金(2012GXNSFBA053006)
段雪峰(1982-),男,湖南祁阳人,教授,博士,研究方向为应用矩阵分析和信息安全。E-mail:zhangxuewwei@163.com
张雪伟,江祝灵,段雪峰.基于Gramian分解的对称半正定矩阵的正则化低秩逼近[J].桂林电子科技大学学报,2015,35(6):419-423.

