基于Davenport风速谱的火箭及其发射平台风致响应分析*
蒋国庆,李道奎(国防科技大学航天科学与工程学院,湖南长沙410073)
基于Davenport风速谱的火箭及其发射平台风致响应分析*
蒋国庆,李道奎
(国防科技大学航天科学与工程学院,湖南长沙410073)
基于Davenport风速谱,采用M.Shinozuka法计算得到了三种不同基本风速下火箭芯级和助推器不同站点的风荷载时程样本,并调用MSC.Nastran软件对火箭及发射平台进行了瞬态响应分析,得到了停靠时不同基本风速下火箭及发射平台的位移响应。随着高度的增加,火箭芯级上各点的位移响应随之增加;不同基本风速下同一节点的最大位移之比约等于不同基本风速的平方之比。同时在脐带塔上设计了一个横拉减载结构,相同基本风速下的火箭位移响应明显减小,火箭及发射平台的抗风能力得到提高,对工程实际有较大的参考价值。
有限元法;风致响应;减载结构
随着人们对火箭运载能力的提高,火箭的尺寸越来越大,部分火箭的高度甚至超过了60m。如此高的火箭在转运或者发射时会有较长时间暴露在近地风中,尤其在海岛等近地风比较大的地方,相对较柔的箭体可能会发生比较大的摆动,这可能导致箭体与摆杆发生碰撞。因此需要对风荷载作用下的火箭位移响应进行计算,并根据计算结果采取相应措施。
近地风具有明显的紊乱性和随机性[1]。高耸结构在近地风作用下,可能产生顺风向、横风向和扭转效应[2],而其风致响应主要是由顺风向湍流引起的[3]。徐旭等[4]通过对比分析采用石沅台风风谱、田浦台风风谱和Davenport风谱[5]计算该结构风载时程及风振响应结果的差异性,得出一些有参考价值的结论。楼文娟等[6]以沿海地区某四回路角钢输电塔为原型建立了有限元模型,采用谐波叠加法生成了B类风场与台风风场下的风速时程,并在时域内对输电塔进行了风振响应和风振系数的数值分析,同时将实验结果与理论计算结果进行了对比分析,验证了数值分析的有效性。本文基于Davenport风速谱,引用M.Shinozuka[7]法计算得到了火箭芯级和助推器不同节点处的脉动风荷载时程曲线,并调用MSC.Nastran软件计算得到了三种基本风速下箭体的位移响应,同时设计一种横拉减载结构,显著减小了火箭的位移响应,为火箭抗风结构的设计提供了一定参考。
1 有限元建模及模态分析
火箭及其发射平台的有限元模型如图1所示,它主要由脐带塔、摆杆、火箭以及发射台组成。采用壳单元模拟脐带塔和发射台的框架,而其加筋结构则采用梁单元进行模拟。火箭箭体采用梁单元进行建模,推进剂采用耦合质量单元进行模拟,这样可以准确地模拟火箭运动时推进剂对箭体横向和对贮箱下椭球底的作用。火箭箭体通过四个支撑座与发射台相连。各级摆杆采用杆单元进行建模,其末端圆弧与火箭外轮廓有0.5m的距离,发射台与脐带塔、各级摆杆与脐带塔均通过多点约束单元RBE2进行连接。

图1 火箭及发射平台有限元模型Fig.1 Finite elementmodel of rocket and its launching platform
为便于后续进行风荷载时程响应分析,需要对火箭及发射平台进行模态分析。火箭及发射平台处于停靠状态,此时发射台下端8个支腿为固支。模型前四阶模态及相应自振频率如表1所示。
由表1可知,火箭及发射平台有限元模型的前四阶模态中,均以火箭振动为主,而其他部分几乎没有振动。
2 近地风荷载的模拟
根据风的周期,可将其分成平均风和脉动风。其中平均风是持续时间大于10min的长周期风,而脉动风的周期很短,通常只有几秒。根据中国荷载规范[8],z高度处垂直于结构表面的平均风压的计算公式为
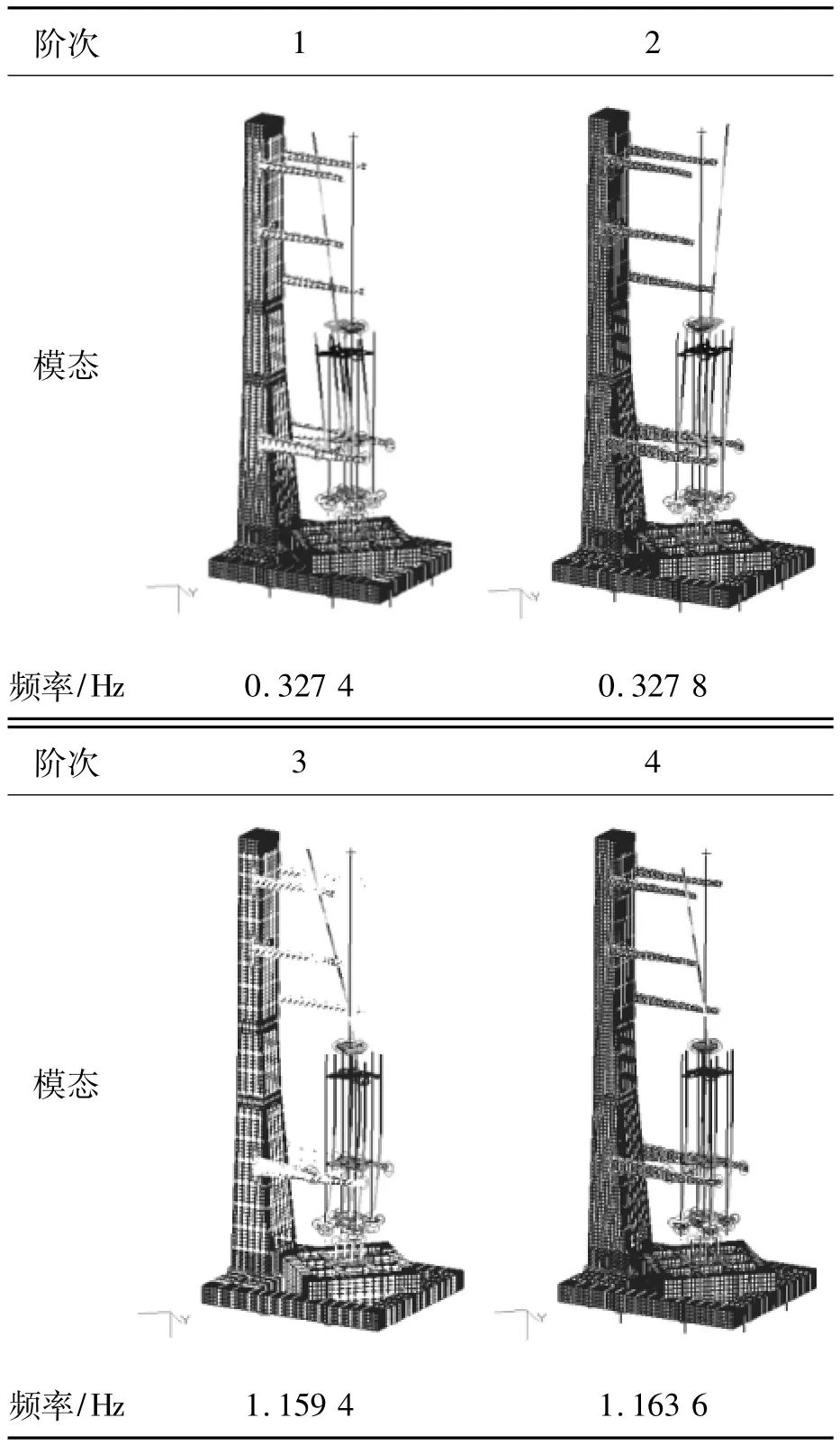
表1 火箭及发射平台前四阶模态及自振频率Tab.1 The first four vibration modes and natural frequency of the rocket and its launching platform

式中,μr为重现期调整系数,μs为风荷载体型系数,μz为风压高度变化系数,w0为基本风压。计算过程中,μr,μs和μz均按照《高耸结构设计规范》[9]进行选取。w0与基本风速¯v0有关,¯v0为当地比较空旷平坦地面、离地10m高、统计50年一遇的10min平均最大风速[9],本次分析了三种基本风速,分别为8m/s,10m/s,13m/s。
脉动风实际是三维的风湍流,主要包括顺风向、横风向和垂直向的湍流[10]。在此只分析火箭及发射平台由顺风向风荷载引起的响应。目前国内外使用最多的是加拿大科学家Davenport经过多次测量得到的脉动风速谱——Davenport风速谱,其功率谱密度函数为

式中:x=1200n/¯v0;k为反映地面粗糙度的系数,根据《高耸结构设计规范》取值;n为脉动风频率,单位Hz。
Davenport风速谱是定义在频域内的,对火箭及发射平台的风致响应分析需要以Davenport风速谱为基础,在时域内对脉动风荷载进行模拟。文献[11]表明谐波合成法中的M.Shinozuka法模拟精度较高,因此本文采用此方法模拟脉动风荷载。由模态分析结果可知,脐带塔、发射台刚度很大,同时各级摆杆迎风面积很小,其所受风荷载相对火箭所受的风荷载而言可以忽略不计。为便于后续计算结果提取,建立如图2所示局部右手坐标系。图2中,火箭的迎风部件为芯级和前两个助推器,后两个助推器背风,暂不考虑其所受风荷载,同时暂不考虑火箭芯级与助推器、助推器与助推器、脐带塔与火箭等相互之间对风湍流的影响。火箭芯级共113个站点,助推器共53个站点,芯级和助推器所受的风荷载需分别计算。根据M.Shinozuka法的计算公式,采用MATLAB编程计算可以得到三种风速下各个站点所受的脉动风荷载,以芯级Node1(即火箭顶端站点)为例,基本风速为8m/s时其脉动风荷载时程曲线如图3所示。

图2 火箭及发射平台受风示意图Fig.2 The schematic diagram of the wind load blowing to the rocket and its launching platform
3 顺风向风振响应分析
对于火箭及发射平台这种大规模模型而言,采用解析的方法求解其动力响应不仅烦琐,而且效率低下,而用数值方法中的有限元法得到的动力响应不仅效率高,计算结果也更可靠。因此采用MSC.Nastran软件对火箭顺风向风致响应进行分析。发射平台底端8个支腿设置为固支,同时把不同基本风速下计算得到的芯级和助推器的风荷载时程曲线分别导入到MSC.Patran软件中,并加载到相应站点上。同时,需要把各个站点受到的平均风荷载加到站点上。设置完毕后,调用MSC.Nastran软件对不同基本风速下的火箭及发射平台有限元模型分别进行计算。计算完毕后,通过MSC.Patran软件的后处理程序对计算结果进行处理。
各级摆杆上装有大量电缆以及其他设备,工程设计人员关心的是箭体在风荷载作用下会不会与摆杆发生碰撞。各级摆杆末端圆弧与火箭外轮廓之间的初始距离为0.5m,如果箭体摆动的幅度大于0.5m,即发生碰撞,摆杆等则需要重新设计。为便于后文的撰写,现把各级摆杆末端所对应的芯级节点编号统计如表2所示。

图3 基本风速为8m/s时Node1风荷载曲线Fig.3 Wind load curve of Node 1 whenthe basic speed is 8m/s

表2 各摆杆末端所对应的芯级节点编号统计表Tab.2 Node numbers of the rocketwhich are close to the end of oscillating bars
基本风速为8m/s时,整流罩摆杆末端节点(Node16)的Y向位移(模型各节点的Y向位移均远大于其他两向,以下均只给出Y向位移)如图4所示。由图4可知,摆杆的位移可忽略不计,因此下面在计算摆杆圆弧与箭体外轮廓之间的距离时不再考虑摆杆的位移。图5为各级摆杆末端所对应的芯级节点的Y向位移曲线,各节点的最大位移统计如表3所示,其中Dmax为各节点Y向最大位移。

图4 基本风速为8m/s时Node16的Y向位移曲线Fig.4 Displacement curve at Y direction of Node16 when the basic wind velocity is 8m/s

图5 基本风速为8m/s时各点Y向位移曲线Fig.5 Displacement curve at Y direction of each node when the basic wind velocity is 8m/s

表3 基本风速为8m/s时各节点Y向最大位移Tab.3 Maximal displacement at Y direction of each node when the basic wind velocity is 8m/s
由表3可知,芯级上四个节点中,离地高度越大的节点其位移越大,相应的各节点与摆杆之间的距离也就越小,但这四个位置的摆杆与火箭均不会发生碰撞。对于不同的基本风速,在此只给出Node12的Y向位移曲线,如图6所示。
对图6进行统计,可以得到不同基本风速下Node12的最大位移、平均位移,如表4所示,其中Dave为Y向平均位移。
由图6和表4可知,不同基本风速下Node12的位移曲线形状基本相同,均表现为不同时刻的位移在平均位移处上下浮动,且除开始阶段浮动幅度比较大外,其余时刻浮动幅度都比较小。这说明在火箭的风振位移响应中,平均风产生了平均位移,脉动风产生了位移的脉动部分。初始时刻突然加在火箭上的平均风在过渡阶段产生了比较大的位移浮动,随着时间的推移平均风产生的位移进入稳态阶段,此时平均风产生的位移即为平均位移。脉动风为各态历经的随机过程,它所产生的位移均值为0m。经过计算,可得132/102=1.69,0.201 7/0.118 5=1.702 1;102/ 82=1.562 5,0.118 5/0.077 2=1.535 0。由前面计算结果可得到如下式子
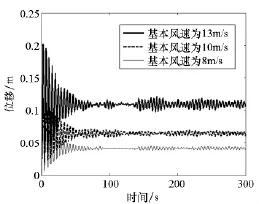
图6 三种基本风速下Node12的Y向位移曲线Fig.6 Displacement curves at Y direction of Node12 under three basic wind velocities

表4 三种基本风速下Node12的Y向位移统计表Tab.4 Displacement statistic at Y direction of Node12 under three basic wind velocities

式中:¯v0i,¯v0j为不同基本风速;Di,max,Dj,max为不同基本风速下火箭上相同节点产生的最大Y向位移。由式(3)可知,随着基本风速的增加,火箭各节点的最大位移也随之增大,例如当基本风速为20m/s时,Node12的最大Y向位移为0.474m。虽然此时摆杆末端圆弧与火箭外轮廓之间的距离依然小于0.5m,但箭体内部分设备会受到一定影响,因此当基本风速较大时需要采取减载措施,减小箭体的位移响应。
4 横拉减载结构设计
在设计横拉减载结构时,需要考虑如下两点:①由于减载结构安装在脐带塔上,因此不能太重,其对减载结构与脐带塔连接处所产生的力不能超过连接处的承受能力;②其必须具有收缩功能,当火箭发射时能自然放下。根据实际情况,设计出如图7所示的减载结构,该结构工作时收缩装置处于锁死状态,故在此没有给出收缩装置示意图。

图7 横拉减载结构Fig.7 Load-reliving structure
设计好减载结构后,需要考虑其安装位置,此时需要考虑如下几点:①安装位置不能离地太高,否则会增加安装难度;②安装位置不能离地太低,否则减载效果不明显;③工作范围内不能与脐带塔上现有的各级摆杆产生干涉,也不能与火箭任何部位产生干涉。综合考虑以上3点,把横拉减载结构安装在芯二级燃箱上。由于之前火箭的有限元模型采用的是梁单元进行建模,为便于减载结构与火箭芯级连接,需要对部分芯二级燃箱重新建模,如图8所示。该部分芯二级燃箱采用壳单元建模,并采用RBE2单元与上下部段连接,其质量为原站点质量,其上所受的载荷等效至邻近的站点上。

图8 部分芯二级燃箱三维有限元模型Fig.8 Three-dimension finite elementmodel of part of the rocketwhere the fuel container is placed
考虑到基本风速为13m/s时火箭顶端的位移响应比较大,在此计算一下此基本风速下减载结构的减载效果。设置完毕后,调用MSC.Nastran进行瞬态响应分析。随后提取Node12的计算结果与无减载结构时该节点的计算结果进行比较,如图9所示。对图9中重要结果统计如表5所示。
由表5可知,脐带塔上装有减载结构后,Node12的Y向最大位移减小了57%,说明设计的横拉减载结构是有明显效果的。

图9 有无减载结构时Node12 Y向位移曲线Fig.9 Displacement statistic curve at Y direction of Node12 with or without load-reliving structure

表5 有无减载结构时Node12 Y向位移统计表Tab.5 Displacement statistic at Y direction of Node12 with or without load-reliving structure
5 结论
建立了一套基于Davenport风速谱的火箭及其发射平台风致响应分析方法和减载结构设计方法,首先基于Davenport风速谱采用M.Shinozuka法计算得到不同基本风速下火箭芯级和助推器各站点上的风荷载时程曲线,最后利用商用软件进行瞬态响应分析,得到如下结论:
1)当基本风速为8m/s,10m/s,13m/s时,脐带塔上各级摆杆末端圆弧均不会与火箭芯级或者助推器发生碰撞,但随着基本风速的增大,两者之间的距离随之减小。
2)本文设计的横拉减载结构能显著减小火箭顶端的位移响应,在一定程度上能保证设备的正常工作,这能为工程实际提供一定参考。
References)
[1]张志强.合肥电视塔风振及地震响应的振动控制研究[D].南京:东南大学,2003.ZHANG Zhiqiang.Studies of wind-induced and seismic vibration control of Hefei TV tower[D].Nanjing:Southeast University,2003.(in Chinese)
[2]王世村.高耸结构风振响应和风振疲劳研究[D].杭州:浙江大学,2005.WANG Shicun.Studies of wind-induced vibration and windinduced fatigue on high-rise structures[D].Hangzhou: Zhejiang University,2005.(in Chinese)
[3]徐旭,杨方勤,屈应辉.结构横风向非平稳随机振动的矩分析[J].非线性动力学学报,2004,11(12):19-30.XU Xu,YANG Fangqin,QU Yinghui.Moment analysis of nonstationary random vibration of flexible structure in crosswind direction[J].Journal of Nonlinear Dynamics in Science and Technology,2004,11(12):19-30.(in Chinese)
[4]徐旭,刘玉.高耸结构在台风作用下的动力响应分析[J].建筑结构,2009,39(6):105-109.XU Xu,LIU Yu.Dynamic response analysis of a high-rising structure under typhoon[J].Journal of Building Structure,2009,39(6):105-109.(in Chinese)
[5]Davenport A G.The spectrum of horizontal gustiness near the ground in high winds[J].Quarterly Journal of the Royal Meteorological Society,1961,8(7):194-211.
[6]楼文娟,夏亮,蒋莹,等.B类风场与台风风场下输电塔的风振响应和风振系数[J].振动与冲击,2013,32(6): 13-17.LOU Wenjuan,XIA Liang,JIANG Ying,et al.Windinduced response and wind load factor of transmission tower under terrain Bwind field and typhoon wind field[J].Journal of Vibration and Shock,2013,32(6):13-17.(in Chinese)
[7]Shinozuka M,Jan C M.Digital simulation of random processes and its applications[J].Sound and Vibration,1972,25(1):111-128.
[8]黄本才.结构抗风分析原理及应用[M].上海:同济大学出版社,2001.HUANG Bencai.The principle and application of structural wind resistance analysis[M].Shanghai:Tongji University Press,2001.(in Chinese)
[9]GB50153-2006.高耸结构设计规范[S].北京:中国计划出版社,2007.GB50153-2006.Code for design of high-rising structures[S].Beijing:China Planning Press,2007(in Chinese)
[10]瞿伟廉,王墨耕.高层建筑高耸结构的风振控制和设计[M].武汉:武汉测绘科技大学出版社,1991.QU Weilian,WANG Mogeng.Wind vibration control and design of high-rising building and structure[M].Wuhan: Wuhan Technical University of Surveying and Mapping Press,1991.(in Chinese)
[11]张志强,李爱群,蔡丹绎,等.合肥电视塔人造脉动风荷载的仿真计算[J].东南大学学报(自然科学版),2001,31(1):69-73.ZHANG Zhiqiang,LIAiqun,CAIDanyi,etal.Simulation of dynamic wind load on the Hefei television tower[J].Journal of Southeast University(Natural Science Edition),2001,31(1):69-73.(in Chinese)
W ind-induced responses of a rocket and its launching p latform based on Davenport w ind speed spectrum
JIANG Guoqing,LIDaokui
(College of Aerospace Science and Engineering,National University of Defense Technology,Changsha 410073,China)
On the basis of Davenportwind speed spectrum and using M.Shinozukamethod,samples ofwind load were numerically simulated on the differentgirds of rocket core and booster under three basic wind velocities.Then a transient response analysiswasmade to the rocketand its launching platform by invoking the MSC.Nastran,and the displacement response of the rocketand its launching platform under differentbasic wind velocities was obtained.The value of the displacement increases along with the increase of height away from the ground,and the ratio of the maximal displacement approximates to the ratio of the square of basic wind velocity on a grid.Finally,a designed load-relieving structure was placed on the umbilical cord tower.Results indicate that themaximal displacement on different grids decreases conspicuously and the anti-wind capability of the rocket and its launching platform are enhanced by a large margin with the help of the load-relieving structure.The designed structure can make a reference to the engineering practice.
finite elementmethod;wind-induced response;load-relieving structure
V435
A
1001-2486(2015)05-104-06
10.11887/j.cn.201505016
http://journal.nudt.edu.cn
2014-12-02
国家973计划资助项目(613277)
蒋国庆(1987—),男,湖南新邵人,博士研究生,E-mail:jieye1987@126.com;李道奎(通信作者),男,教授,博士,硕士生导师,E-mail:lidaokui@nudt.edu.cn

