改进层次分析法在爆破事故分析中的应用
张建华 李泽安
(武汉理工大学资源与环境工程学院)
爆破是矿山生产过程中不可或缺的一个环节,但其具有危险性大、潜在危险源多、易发生事故和产生的事故后果严重等特点,给矿山工作人员的人身安全带来了严重的威胁。在各类生产事故中,爆破事故所占比例高达40%以上[1]。矿山企业能否实现安全爆破,直接影响着员工的安全与健康、企业能否正常生产运营等重要问题。因此通过科学的方法分析矿山爆破事故,确定需要重点解决的问题,然后采取相关措施以提高爆破安全性,是矿山管理人员和爆破人员的基本任务。
目前,爆破事故常用的分析方法有层次分析法、事故树、事件树、鱼刺图法等。其中层次分析法[2]是由美国匹兹堡大学AL Saaty教授于20世纪70年代初提出的,目的是为了解决多目标决策问题,特别是解决一些只能定性无法定量的问题。但传统的AHP方法为了确保排序的准确性,必须要进行一致性检验,如果没有通过检验,需要专家再次打分、调整和计算,而这种调整一般会带来很大的主观性,影响计算结果的准确性和可信度,而且可能需要经过多次计算才可以通过检验[2]。为了解决以上问题,东南大学梁樑教授[3]于1989年提出了一种改进方法,通过引进最优传递矩阵,使之可以不进行一致性检验,经过多次试验,该方法是可行的。因此作者将改进层次分析法运用到爆破事故分析中,既可以避免传统层次分析法的不足,又可以继承其优点。最后结合ABC法,对指标层因素进行等级分类,确定需要重点解决的问题。
1 改进层次分析法
1.1 建立层次结构模型
对所要研究的问题进行深入分析,将问题所包含的各种因素进行归纳,然后将这些因素自上而下分层,上层影响着下层,而层内之间各因素基本上是相对独立的,构造出层次结构模型。层次结构模型一般分为A(最高层)、C(中间层)和P(最低层)3层。A(最高层):决策的目的、要解决的问题;C(中间层):考虑的因素、决策的准则;P(最低层):决策时的备选方案。
1.2 构造判断矩阵F
判断矩阵表示在相同层次中,每个因素相对于上一层次的同一个因素的重要性程度。通常采用1~9标度法。

表1 判断矩阵标度值及其含义
1.3 计算反对称传递矩阵Q
定理 1:设 A=[aij]、B=[bij]、C=[cij]∈Rn×n,若aij=1/aji,则称A为互反矩阵;若bij=-bji,则称B为反对称矩阵;若A为互反矩阵,且aij=aik/ajk,则称A是一致的;若B是反对称阵,且bij=bik+bkj,则称B是传递的。
设 F=[fij]、Q=[qij]、L=[lij]、F*=[fij*]∈Rn×n。
因为 fii=1,fij=1/fji(i,j=1,2,…,n),所以,F为互反矩阵;又fij=fik/fjk,所以F是一致的。
令 Q=lgF(qij=lgfij),则 qij= -qji且 qij=qik+qkj,那么Q为反对称矩阵,并且是传递的。
1.4 计算Q的最优传递矩阵L
1.5 计算拟优一致矩阵F*
定理3:若A是互反矩阵,B=lgA,C是B的最优传递矩阵,那么矩阵A*=10C是A的一个拟优传递矩阵,并且它是一致的。
令F*=10L,则F*是F的拟优一致矩阵。
1.6 用方根法求H*的特征向量W
将F*的元素按行相乘,对乘积分别开n次方。并将方根向量归一化,即得特征向量 W,其中,Wi表示对应元素相对上一层次因素重要性的权重值。
1.7 层次总排序
重复以上步骤,计算P层对于C层的权重值:
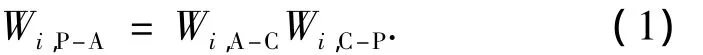
计算P层对于A层的相对重要性次序的权重值,最后根据计算得到的Wi,P-A值进行排序。
1.8 对指标层进行分类
ABC 分类法[4-5]把被分析的对象分成 A、B、C 3类,其中A类表示主要影响因素,B类表示次要影响因素,C类表示一般影响因素。划分的标准是分析对象的累计频率,A、B、C三类累计频率分别为0%~80%、80% ~90%和90% ~100%。由于A、B两类累积频率和大于90%,可以认为其所包含的信息量足以代表全部的信息量,因此在解决实际问题时,只需对A和B两类的指标层采取相应措施,就可以达到改善目标层的目的。
2 案例分析
通过调查分析某矿山近10 a的爆破事故,把影响爆破安全的因素分为爆破设计、爆破操作及安全管理和环境三大类,再细分为安全距离过小、装药量过大、孔网参数设计不合理、抵抗线设计不合理等12个方面。
2.1 层次结构模型建立
通过分析爆破事故,把影响爆破安全的因素进行分类,然后绘制出层次分析模型,见表2。

表2 爆破事故层次结构模型
2.2 构造判断矩阵
根据专家打分,确定各因素之间的相对重要程度,得到表3~表64个判断矩阵。

表3 A-C判断矩阵

表4 C1-P判断矩阵

表5 C2-P判断矩阵

表6 C3-P判断矩阵
2.3 计算过程
下面以计算WA-C为例进行计算。
(1)由判断矩阵FA-C,可以求出反对称传递矩阵QA-C:

(2)计算最优传递阵LA-C:


(4)求特征向量WA-C。
WA-C=[2.4660,1.0000,0.4055]T,归一化,得:

同理,计算P层因素对C层因素的相对权重值得:

2.4 层次总排序
由以上计算结果,利用式(1)计算P层对于A层的权重值。Wi,P-A表示P层因素相对于A层的重要性的总权重值,见表7。
2.5 指标层分类
由表7计算得出的结果绘制出ABC分类图,见图1。

表7 层次总排序
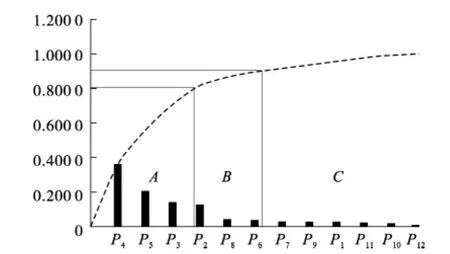
图1 指标层ABC分类结果■—P 权值;---—求和
由图1可以看出,属于A类的指标包括P3孔网参数设计不合理、P4抵抗线设计不合理、P5未按设计连接网络这3个因素;属于B类的指标有P2装药量设计过大、P6未按设计布孔装药、P8起爆前未清点人数等3个因素,其他指标都属于C类。由此可以得出,该矿山需要重点解决的问题是孔网参数设计不合理、抵抗线设计不合理、未按设计连接网络、装药量设计过大、未按设计布孔装药及起爆前未清点人数6个方面。
2.6 分析结果
通过以上分析计算,结合最大隶属度原则得出以下结论:
(1)通过一级目标层权重计算结果得出:爆破设计是影响爆破安全的最大影响因素,所占权重高达0.6370,因此设计人员在进行爆破设计的时候应严谨;其次是爆破操作,所占权重为0.2583,要解决爆破操作人员的不规范化或不合理操作。
(2)从二级指标权重计算结果得出:P3孔网参数设计不合理、P4抵抗线设计不合理、P5未按设计连接网络这3个因素属于A类,P2装药量设计过大、P6未按设计布孔装药、P8起爆前未清点人数属于B类,其他均属于C类。相对于C类来讲,需要重点解决A和B两类所包含的问题,才可以达到安全爆破的目的。
3 总结
通过改进的层次分析法分析某矿山爆破事故,可以得出影响该矿山爆破安全的主要因素是孔网参数设计不合理、抵抗线设计不合理、未按设计连接网络和装药量设计过大等。因此,要提高矿山爆破的安全性,需要重点解决这六个方面的问题。此外,虽然运用改进层次分析法可以快速确定影响爆破安全的主次要因素,而且还可以避免传统层次分析法判断矩阵为通过一致性检验而带来的片面性和主观性,但改进层次分析法也具有其弊端,即在计算权重时可能出现两个或两个以上的权值相同,当出现这种情况,不能保证排序准确性,因此如何避免这一情况还需进一步探讨。
[1] 任玉辉,秦跃平,刘业娇.基于FTA-AHP的矿山爆破飞石伤人事故风险分析[J].现代矿业,2014,539(3):59-61.
[2] 李传哲,于福亮,鲍卫锋,等.改进层次分析法在影响因素分析中的应用[J].节水灌溉,2006(5):47-52.
[3] 谭跃进,陈英武,易进先.系统工程原理[M].长沙:国防科学技术出版社,1999.
[4] 梁 樑,盛昭翰,徐南荣.一种改进的层次分析法[J].系统工程,1989,7(3):5-7.
[5] 侯 茜,李翠平,李仲学.基于库存ABC分类法的矿山物料管理[J].矿业快报,2007,455(3):52-55.

