自适应遗传PID算法在风洞风速控制中的应用

尼文斌, 董金刚, 刘书伟, 贺丽慧, 付增良

(中国航天空气动力技术研究院, 北京 100074)

自适应遗传PID算法在风洞风速控制中的应用

尼文斌, 董金刚*, 刘书伟, 贺丽慧, 付增良

(中国航天空气动力技术研究院, 北京 100074)

风速控制是风洞的核心控制部分，风速控制系统的优劣直接影响风洞性能指标，为了完成FDxx风洞的风速控制系统，设计了一种基于自适应在线遗传算法的PID参数整定方法，在风洞气源资源有限的情况下，快速建立流场，确保流场稳定时间。首先对控制参数进行联合编码，在种群个体进化前期采用锦标赛精英保留策略，后期采用基于轮盘赌非线性选择方法，加快算法收敛速度，同时避免了算法过早陷入局部最优，交叉选用单点交叉，变异采用均匀取反法，动态调整过程为了减小甚至避免超调，采用误差绝对值及误差和误差变化率加权方式设计目标函数，并采取了惩罚措施，即一旦产生超调，将超调量作为最优指标的一项，现场测试验证了算法的可靠性及实用性。

风洞；风速控制；参数调整；PID算法；遗传算法

0 引 言

风洞风速控制系统是风洞控制系统的核心部分，风速控制系统的优劣直接影响风洞性能指标，决定风洞实验能力。风速控制系统要求运行安全稳定，抗干扰能力强，人机接口操作简单方便，功能强大且易于维护升级。

风洞风速控制系统具有滞后性、非线性和参数时变等特点，并且随着模型位姿、气源压力和气压密度等参数的变化，风洞自身参数都会发生改变，所以很难建立精确的数学模型。传统的PID(Proportion Integration Differentiation，比例积分微分)控制方法

1套参数不可能适应所有情况，当风洞参数发生变化时，控制效果会大打折扣。目前国内外采用PID控制策略来实现风速控制，基本都会采用不同的PID参数来对应不同的Ma，甚至一次实验不同阶段也会选择不同的参数，然而PID参数的调试过程不仅耗时耗力而且浪费资源，即便如此，选取的PID参数也只能算相对理想而非最优，如果遇到特殊情况还需重新调整[1-2]。

针对传统PID的局限性，国内外一些风洞风速控制引入了自适应控制、模糊控制和神经网络控制等智能控制策略[3-9]。李可、刘旺开等人依据多年专家经验和领域知识总结出若干条模糊控制规则，将专家模糊控制策略应用于D-4风洞，提高了实验效率和精度，并且指出实际应用中建立模糊规则和隶属函数比较困难[7]；吕鹏涛和惠增宏采用神经网络算法实现NF-3风洞的风速控制，提高了风速大于10m/s时的控制精度，指出神经网络权重初值的选取对于神经元网络的学习效率和收敛速度影响很大，为了防止控制作用引起的系统震荡加入了死区控制，指出死区范围由被控对象决定[8]；R.Mart Rennie采用神经网络构建风洞数学模型实现前馈控制，提高了控制算法的动态特性，指出利用神经网络构建数学模型需要大量数据[9]；M. James McMichael、David E. Parekh等人采用模糊策略构建旋转体气动模型，采用遗传算法对模型参数进行优化，实验获得了良好动态特性、无超调无稳态误差，并且建议模糊遗传工具及其变种应该得到更多的应用[10]。

本文设计了一种自适应在线遗传PID算法，在不依赖专家经验、知识库、被控对象数学模型以及大量仿真数据前提下，成功应用于FDxx风洞，对其PID参数进行在线自整定，当风洞状态参数发生改变时，算法可以实时调整输出，具有较强的鲁棒性。

1 FDxx风洞简介

FDxx风洞是暂冲式超声速风洞，Ma=1.5、2.0、2.5，试验段截面尺寸：0.2m×0.2m；有效工作时间：t≥15s。总体布局图如图1所示，包括气源系统、阀门系统、稳定段、收缩段、喷管段、试验段、超声速扩散段、亚声速扩散段以及消音塔。

FDxx风洞工作介质为压缩空气，气源系统由压缩机、冷冻式空气干燥机以及储气罐组成。气源额定压力为1.8MPa，设计压力为1.3MPa，气源容积为18m3，为确保较长的有效工作时间，要求流场调节系统在确保精度的前提下，动态响应足够快。

图1 FDxx暂冲式超声速风洞总体布局

2 测控系统组成

FDxx风洞测控系统主要任务：一是控制调压阀的开度，确保前室总压稳定；二是完成风洞数据采集、数据处理以及数据保存。

测控系统由工控机、模拟量输入输出卡、继电器、电机及驱动器、压力传感器和高精度电位器等设备组成。如图2所示，PCI-9111卡采集的前室总压信号为被控量，工控机依据此信号调节控制器输出，控制电机运行方向以及转速，间接控制调压阀开度，从而影响总压，使总压维持在某一数值，最终确保风洞试验段流场品质满足要求。

图2 风洞测控系统框图

3 控制算法分析和仿真

3.1 增量式PID控制算法分析

PID控制不需要建立精准的数学模型，通过调整控制器的结构和参数便能满足大多数性能要求，原理简单、易于实现、可靠性强[1-2]。PID控制器由比例环节、积分环节和微分环节组成，如图3所示：

图3 PID控制系统原理图

连续PID离散化处理后便可通过计算机程序实现，由于计算机实现的数字PID灵活性大，产生了一系列改进的PID控制算法，其中增量式数字PID算法不需要累加，控制增量仅与最近k次采样有关，误动作影响小，较易通过加权处理得到比较好的控制效果[11]，因此选择该算法作为FDxx风洞现场调试的保底兼对比控制算法，其方程为：

(1)

3.2 自适应遗传PID算法分析

遗传算法应用于数字PID控制器时流程图如图4所示。所谓在线遗传PID整定，即在每个采样时刻实现PID参数的遗传算法优化[12-18]，具体操作方式为：

图4 遗传算法PID参数整定流程图

(1) 联合编码：选用搜索能力较强的二进制编码方式对PID控制参数进行联合编码，为克服二进制编码存在的Hamming悬崖缺点，采用二进制Gray编码方式；

(2) 选择操作：选择前期采用锦标赛精英保留策略，剔除劣势个体，后期采用基于轮盘赌的非线性选择方式，增加种群多样性，加快进化速度；

(3) 交叉操作：交叉选用单点交叉，即依据概率选择一对父向量的一部分分量，将这部分分量进行交换生成一对新向量；

(4) 变异操作：变异采用均匀取反法，即依据概率选择一个父向量的一部分分量，然后将这部分分量取反； (5) 算法参数：用长度为16位的格雷码来表示3个决策变量kp、ki和kd，种群规模定Size=100，交叉率Pc=0.7，变异概率初值Pm=0.05且随适应度函数发生变化，最大进化代数为80。

为了得到较优的动态过渡特性，并减小甚至避免产生超调，采用误差绝对值及误差和误差变化率加权和作为第k次采样时刻第i个个体的参数选择最小目标函数：

(2)

式中：e-ki(t)为第k次采样时刻第i个个体误差；de-ki(t)为第k次采样时刻第i个个体误差变化率；αp,βp为权值。

为减小甚至避免超调，采取惩罚措施，即产生超调后，将超调量作为最优指标的一项，此时最优目标函数为：

(3)

对于每个采样时刻，计算当代种群所有个体的自适应度函数，选择自适应度大的个体解码，其对应的PID控制参数即为该采样时刻下的控制参数。

3.3 数学建模与控制算法仿真

FDxx风洞采用无刷直流伺服电机控制调压阀动作，电机系统原理如图5所示。

图5 电机系统原理图

如图6所示，采用Matlab/Simulink搭建电机控制模型[19-20]，采用“MATLAB Fcn”模块编写遗传PID控制算法。图6中涉及的主要参数意义为：GA-PID为控制算法为自适应遗传PID算法；Population size、crossing-over rate、mutation rate、adaptive learning为遗传算法参数；disturbance为干扰状态参数；with PID output为PID输出是否参与学习开关。

MATLAB仿真采样频率为1kHz，在每个采样时刻对PD参数进行遗传算法优化，公式(2)最小目标函数中，取αp=1.1，当误差e-ki(k)小于0.6时，取βp=0.05，当误差e-ki(k)大于0.6时，取βp=0。种群规模Size=100，最大进化代数为80，交叉概率Pc=0.7，采用自适应变异概率方法，即变异概率与自适应度成反比，变异概率Pm=0.05-[1∶Size]×0.025/Size。为了减少寻优的盲目性减少计算量，限定参数kp的取值范围为[10.0,15.0]，kd取值范围为[0.15,0.25]，然后再在这组参数周围按照遗传算法进行自适应调节，整定结果如图7所示。

在控制初始阶段，为了迅速追踪输入信号降低误差，kp增大kd减小，当kp上升到一定程度，为了防止误差变化太快产生超调，kp减小kd增大，当误差小

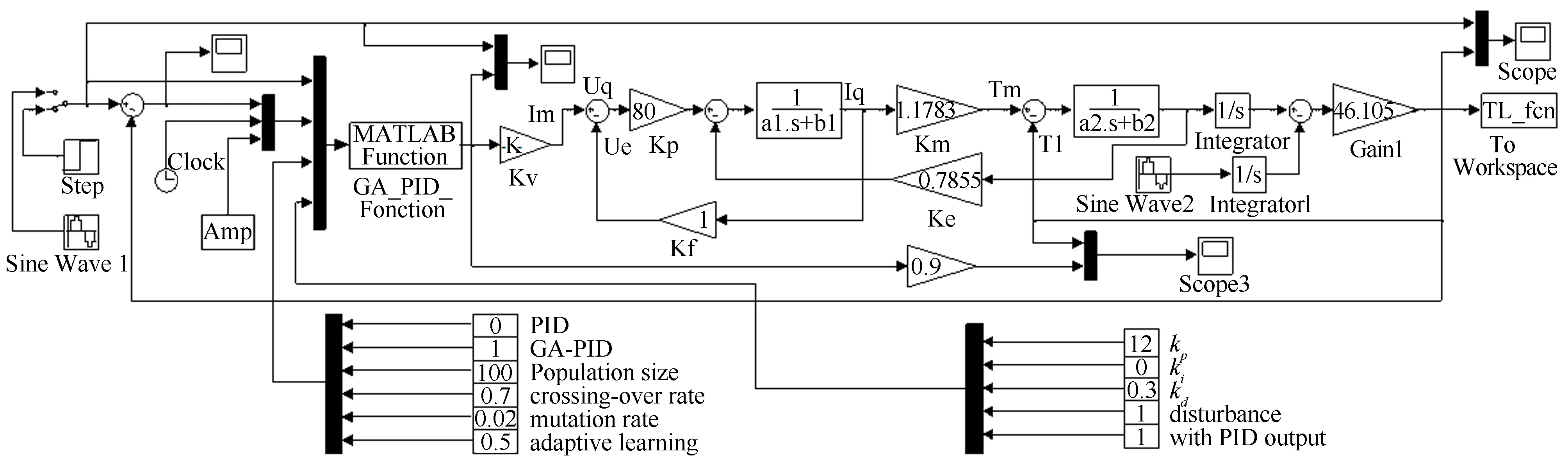
图6 Simulink实现遗传PID控制算法

图7 仿真数据

于某一值时，kp和kd最终趋于稳定，最终稳态控制精度在0.5%以内。

4 现场调试结果

图8所示为FDxx暂冲式超声速风洞，超声速Ma调节取决于喷管，流场调节只需控制前室总压高于某一数值并且维持稳定，便可在试验段建立流场，不同Ma要求前室总压最小值不同，并且前室总压大小与试验工作时间成反比，由于气源容积有限，为了确保有效工作时间，将前室总压设置为一个比较大的数值来满足所有Ma方案不可取，理想方案为不同Ma对应不同前室总压，所以流场控制算法需要快速跟随任意给定前室总压并且维持稳定。

考虑到不同Ma要求不同前室总压，实验时选择了400kPa和252kPa 2个给定总压，分别采用增量式PID算法和自适应遗传PID算法进行调试。图9为一次现场调试程序截图。

图8 FDxx暂冲式超声速风洞

图9 自适应遗传PID现场调试截图

图10所示为增量式PID控制算法4次实验数据。给定总压为400kPa，调试PID参数kp=12，ki=5，kd=0.5，现场实际采样频率为10Hz。控制效果如图10所示，红色和蓝色曲线快速收敛无震荡，总压稳定调节时间在2s以内，控制效果比较理想；PID参数不变，给定总压变为252kPa时，图10中黑色和绿色曲线均发生不同程度的震荡，调节时间增加到4s左右，控制效果变差，数据表明，增量式PID算法1套PID参数不能满足所有的给定总压，即不同的Ma需要不同的PID参数，增加了工作量和调试难度。

图10 增量式PID算法调试数据

现场调试时还发现相同PID参数、相同给定总压，气源压力分别为12MPa和13MPa时，控制效果也略有差异，图10中红色和蓝色曲线超调量不同，绿色和黑色曲线动态调整过程不同，数据表明气源压力会对增量式PID算法产生一定影响，算法抗干扰能力差，鲁棒性弱。

图11所示为自适应遗传PID算法4次测试数据，均采用长度为16的格雷码对控制参数kp、ki和kd进行编码，种群规模100，交叉率0.7，变异概率初值为0.05且随适应度函数发生变化，最大进化代数80，其他实验条件也均相同。

图11 自适应遗传PID算法调试数据

由图11的测试数据可以看出，无论给定总压为252kPa还是400kPa，无论气源压力为12MPa还是13MPa，总压均能快速收敛无震荡，调节时间均在2s左右，动态调整过程相似，改变Ma或者气源压力时，不需要调整算法参数。图11小图显示系统稳定后前室总压波动范围在2kPa以内，稳态控制精度在0.8%以内，该精度受总压传感器性能及控制系统硬件性能影响较大，在有限的硬件资源下，该控制效果比较理想。

实验数据可以证明，自适应遗传PID算法在FDxx风洞风速控制中几乎不受给定总压和气源压力参数变化的影响，鲁棒性好，适应性强。

5 结 论

FDxx风洞风速调试数据表明：

(1) 增量式PID控制算法用于流场调速，受气源压力、给定总压等风洞参数影响较大，同一套PID参数很难在所有情况下均获得较好的控制效果。

(2) 选用增量式PID算法用于流场调速，想要达到较好的控制效果，需要在不同的工况下，选择不同的PID参数，调试难度大并且不可能涵盖所有工况。

(3) 自适应遗传PID算法用于流场调速，鲁棒性好，适应性强，控制效果几乎不受风洞参数影响。

[1] 褚卫华, 汤更生, 王帆. 2m×2m超声速风洞流场控制策略研究与实现[J]. 实验流体力学, 2012, 26(5): 98-102.

Chu Weihua, Tang Gengsheng, Wang Fan. Research and realization on the control strategies of the 2m×2m supersonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(5): 98-102.

[2] 郝礼书, 乔志德, 张永双, 等. NF-6风洞马赫数闭环控制系统设计研究[J]. 实验流体力学, 2010, 24(4): 85-88.

Hao Lishu, Qiao Zhide, Zhang Yongshuang, et al. Design research on the Mach number closed-loop control system in the NF-6 wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(4): 85-88.

[3] Mark J Balas, Nailu Li. Adaptive control of flow over a wind turbine blade[R]. AIAA-2012-4857, 2012.

[4] 李建新, 王书鹏, 袁镇福. 高温多相流风洞模糊PID自整定神经元解耦补偿控制[J]. 热力发电, 2010, 39(8): 23-27.

Li Jianxin, Wang Shupeng, Yuan Zhenfu. Fuzzy PID self-regulation neuron decoupling compensation control in high-temperature multiphase flow wind tunnel[J]. Thermal Power Generation, 2010, 39(8): 23-27.

[5] Narendra K Beliganur, Raymond P LeBeau. Application of genetic algorithms and neural networks to unsteady flow control optimization[R]. AIAA-2007-3826, 2007.

[6] 赵书军, 施洪昌, 冷崇珍, 等. 神经网络在风洞流场马赫数辨识中的应用研究[J]. 流体力学实验与测量, 2004, 18(3): 87-91.

Zhao Shujun, Shi Hongchang, Leng Chongzhen, et al. Research of application of neural network in Mach number identification of wind tunnel flow field[J]. Experiments and Measurements in Fluid Mechanics, 2004, 18(3): 87-91.

[7] 李可, 刘旺开, 王浚. 专家-模糊PID在低速风洞风速控制系统中的应用[J]. 北京航空航天大学学报, 2007, 33(12): 1387-1390.

Li Ke, Liu Wangkai, Wang Jun. Parameters self-tuning fuzzy PID combined with expert control on wind velocity control system of wind tunnels at home[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(12): 1387-1390.

[8] 吕鹏涛, 惠增宏. NF-3风洞神经网络自适应稳风速控制系统研制[J]. 实验流体力学, 2009, 23(4): 82-86.

Lyu Pengtao, Hui Zenghong. The development of wind velocity adaptive control system based on neural networks for NF-3 wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2009, 23(4): 82-86.

[9] Mark R Rennie, Peter Sutcliffe. Neural-network control of wind tunnel test conditions[R]. AIAA-2014-2109, 2014.

[10] James M McMichael, David E Parekh, Michael Heiges, et al. Genetic and fuzzy approaches to flow control[R]. AIAA-2002-3072, 2002.

[11] 刘金坤. 先进PID控制MATLAB仿真[M]. 北京: 电子工业出版社, 2011: 27-27.

Liu Jinkun. Advanced PID control and MATLAB simulation[M]. Beijing: Electronics Industry Press, 2011: 27-27.

[12] Tang Hongwu, Xin Xiaokang, Dai Wenhong, et al. Parameter identifica for modeling river network using a genetic algorithm[J]. Journal of Hydrodynamics, 2010, 22(2): 246-253.

[13] Wang Hongbin, Liu Mian. Design of robotic visual servo control based on neural network and genetic algorithm[J]. International Journal of Automation and Computing, 2012, 9(1): 24-29.

[14] Concha Bielza, Pedro Larranaga. Parameter control of genetic algorithms by learning and simulation of bayesian networks-a case study for the optimal ordering of tables[J]. Journal of Computer Science and Technology, 2013, 28(4): 720-731.

[15] Wang Tong, Chi Qingguang, Liu Chunfang. Parameter identification and compensation control of friction model for PMSLS based on genetic algorithms[C]//Proceedings of 2010 Chinese Control and Decision Conference, Xuzhou, Jiangsu, 2010.

[16] Zhao Weilun, Wang Yan, Zhou Yucheng, et al. Researches on the mixture compensating method based on dynamic neural net-

work and genetic algorithm[C]//Proceedings of the 2011 Chinese Control and Decision Conference, Mianyang, Sichuan, 2011.

[17] Xia Yimin, Zhang Gangqiang, Nie Sijun, et al. Optimal control of cobalt crust seabed mining parameters based on simulated annealing genetic algorithm[J]. J Cent South Univ Technol, 2011 18: 650-657.

[18] Li Na, Lyu Lixia. Parameter optimization for turbine DEH control system based on improved genetic algorithm[C]//Proceedings of 2010 Chinese Control and Decision Conference, Xuzhou, Jiangsu, 2010.

[19] 张学军, 陈永禄, 蒋占军, 等. 基于遗传算法的航空发电控制系统仿真研究[J]. 兰州交通大学学报, 2010, 29(6): 83-86.

Zhang Xuejun, Chen Yonglu, Jiang Zhanjun, et al. Simulation of aeroplane generator control system based on genetic algorithm[J]. Journal of Lanzhou Jiaotong University, 2010, 29(6): 83-86.

[20] Ebrahim Ghotbi Ravandi, Reza Rahmannejad, Amir Ehsan Feili Monfared, et al. Application of numerical modeling and genetic programming to estimate rock mass modulus of deformation[J]. International Journal of Mining Science and Technology, 2013, 23: 733-737.

(编辑：杨 娟)

Application of PID based on adaptive genetic algorithms in wind velocity control system of wind tunnels

Ni Wenbin, Dong Jingang*, Liu Shuwei, He Lihui, Fu Zengliang

(China Academy of Aerospace Aerodynamics, Beijing 100074, China)

In order to accomplish the wind speed control system for a FDxx wind tunnel, a PID parameter setting method based on adaptive online genetic algorithm was designed. In the case of the limited gas source for a wind tunnel test, the algorithm can quickly establish the flow field and ensure the stability time of the flow. First, joint coding is done with these parameters. With elitist strategy adopted in early genetic evolution stage, a non-linear selection method based on roulette selection is introduced in the last period. So optimum individuals are preserved and the population diversity is increased. The fixed value thus would not be exceeded in the dynamic adjustment process. The objective function is set up with the error absolutes and variation rate accompanied by penalty functions. When the fixed value is exceeded, the excess is taken as the optimal. This method has been applied in a field debugging of FDXX wind tunnel. The result shows that it is fast, effective and reliable to use online adaptive genetic algorithms to set the PID control parameters.

wind tunnel;wind velocity control;parameter setting;PID algorithm;genetic algorithm

1672-9897(2015)05-0084-06

10.11729/syltlx20150016

2015-01-27;

2015-07-07

国家自然科学基金(11302214)

NiWB,DongJG,LiuSW,etal.ApplicationofPIDbasedonadaptivegeneticalgorithmsinwindvelocitycontrolsystemofwindtunnels.JournalofExperimentsinFluidMechanics, 2015, 29(5): 84-89. 尼文斌, 董金刚, 刘书伟, 等. 自适应遗传PID算法在风洞风速控制中的应用. 实验流体力学, 2015, 29(5): 84-89.

TP273

A

尼文斌(1986-)，山东烟台人，助理工程师。研究方向：智能检测与运动控制。通信地址：北京市丰台区云冈西路17号7201信箱12分箱(100074)。E-mail: nwb.0919@aliyun.com

*通信作者 E-mail: djg0927@sina.com