高速风洞连续变速压颤振试验技术研究

郭洪涛, 闫 昱, 余 立, 吕彬彬, 杜 宁

(1. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000; 2. 中国空气动力研究与发展中心 高速空气动力研究所, 四川 绵阳 622763)

高速风洞连续变速压颤振试验技术研究

郭洪涛1,2,*, 闫 昱2, 余 立2, 吕彬彬2, 杜 宁2

(1. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000; 2. 中国空气动力研究与发展中心 高速空气动力研究所, 四川 绵阳 622763)

针对高速暂冲式风洞阶梯变速压颤振试验用时长、耗气量大和试验模型有效使用寿命短等缺点，开展了高速暂冲式风洞连续变速压颤振试验技术研究，解决了定Ma数连续变速压流场控制技术与连续变速压工况下的颤振试验数据处理技术等难题。具体技术措施是：在2.4m×2.4m暂冲式跨声速风洞中设计了基于运动函数的定Ma数线性变总压控制策略，使Ma数控制精度达到了0.005以内且速压无超调，实现了流场控制目标；采用Pick-Hold方法构建颤振边界的亚临界预测判据，并根据预测判据近似于正态分布的特点，基于数理统计的参数估计法来减小预测判据的散布度，从而提高颤振边界亚临界预测的准确性。风洞验证试验结果表明，该试验技术达到了工程实用化水平，不仅能够取得与阶梯变速压颤振试验技术一致的结果，还能极大地节省耗气量，经济效益显著。

颤振；气动弹性；风洞试验；试验技术；流场控制

0 引 言

颤振是飞行器气动力、弹性力和惯性力相互耦合引发的一种自激发散振动，严重时可导致飞行器空中解体。颤振边界决定飞行包线范围，影响作战性能，是先进飞行器结构设计必须考虑的关键因素。因此，准确预测颤振边界是飞行器研制中必须解决的重大技术问题。获取飞行器颤振边界主要有计算和试验2种手段。颤振计算主要针对亚声速与超声速情况，而对于跨声速范围的颤振，由于流动的复杂性，目前的数学模型和硬件设备还无法给出准确可靠的结果。颤振风洞试验则可以利用风洞再现颤振现象，校核颤振边界，研究颤振特性，其结果也为颤振飞行试验提供依据[1-2]。

在高速风洞颤振试验领域，国内通常的做法是采用定Ma数阶梯变速压的开车方式来获取颤振边界。设置速压阶梯的目的是获取一定长度的振动信号数据，然后采用基于平稳随机信号的数据处理方法来计算颤振稳定性参数。然而，在确保试验结果精准度的前提下，相对阶梯变速压颤振试验方法来说，连续变速压颤振试验方法具备3大优势：(1)试验时间短，耗气量小，经济效益显著；(2)颤振边界预测参数曲线更加光滑连续，试验结果信息量更大；(3)试验速压可连续逼近颤振临界点，避免阶梯变速压工况下的超临界情况，试验安全性更高。

随着风洞流场控制技术与测试设备性能的不断提升，以及非平稳信号分析理论的提出，国外率先开始发展基于非平稳随机信号数据处理的连续变速压颤振试验方法。1990年，NASA兰利研究中心的Robert V报道了可用于连续变速压颤振试验的亚临界分析方法[3]，即Pick-Hold方法。该方法从理论上分析了速压与颤振模型振动能量的关系，并和其它方法作了比较研究。1994年7月，洛克希德马丁公司在NTS的4ft×4ft亚跨超三声速风洞中采用连续变速压颤振试验方法进行了F-22的垂尾颤振试验，并获得了需要的硬颤振点[4]。日本国家宇航实验室的Yuji Matsuzakai于1998年提出了DTFM(Discrete Time Flutter Margin)方法[5]，该方法基于ARMA模型获得连续变速压颤振试验数据的稳定性参数，与阶梯变速压方法不同的是，稳定性参数随速压变化是一条连续线。1999年，该方法成功应用于一个超声速斜置翼的颤振试验[6]。但是，通过理论分析与数值仿真，笔者发现ARMA模型对于同时有输入与输出数据的系统具有一定的适用性，对于只有输出响应的连续变速压颤振试验数据其应用效果则欠佳，这在NASA的Robert Walker等人的研究中也得到了证实[7]。

本文基于国内外相关研究成果与已有技术基础，在流场控制方面，设计基于运动函数的定Ma数线性变总压控制策略，实现2.4m跨声速风洞的定Ma数连续变速压流场控制；在数据处理技术方面，提出一种连续变速压颤振试验数据的预处理方法，基于Pick-Hold方法构建颤振边界的亚临界预测判据，并根据预测判据随速压的变化近似于正态分布的特点，利用数理统计理论的参数估计方法减小预测判据的散布度，以提高连续变速压试验工况下颤振边界亚临界预测的可靠性。

1 试验设备与方法

1.1 风洞与模型

本研究在中国空气动力研究与发展中心高速所的2.4m×2.4m风洞(FL-26风洞)半模试验段中进行。该风洞是一座试验段横截面为2.4m×2.4m的引射式、半回流、暂冲型跨声速风洞。试验Ma数范围为0.3～1.4。半模试验段上、下壁开有与气流方向成60°、直径为24mm的斜孔，主要目的是消除跨声速时的激波反射干扰；左右侧壁为实壁，左侧有转窗机构，右侧有随动转窗壁，可以实现安装于侧壁模型迎角变化。

研究模型为大展弦比超临界机翼，该模型是满足气动外形、刚度分布和质量分布相似的动力学相似模型。为了模拟机身的气动影响，机翼通过刚性机身与风洞侧壁转窗连接。根据机翼模型结构设计布局，模型采用铝合金单梁加复合材料应力蒙皮形式，内部填充聚胺脂泡沫。各个梁、肋的截面尺寸和蒙皮厚度均由模态优化计算后的结果确定，梁与肋之间靠角片连接，连接后缝隙用环氧树脂胶接，蒙皮与梁、肋之间主要靠环氧树脂胶接。结构设计完成后的模型梁、肋示意如图1所示。

图1 模型内部结构示意图

经过优化，模型设计结果的前3阶模态频率与真实飞机误差小于1.2%，模态置信判据(MAC)矩阵对角线值大于0.96。经过地面模态试验检测，实际加工得到的模型前3阶模态频率误差小于6%。具体结果如表1所示。

表1 模型的模态设计及检测结果

1.2 测试仪器

试验时，采用粘贴于主梁上的电阻丝应变计(中国航空集团制造，EF1000-4AA-AM(11)-X)来测量机翼的弯曲与扭转变形；采用安装于翼尖的加速度传感器(美国Entran公司制造，EGAX-100-C20001)来测量机翼的振动加速度。数据采集系统采用美国国家仪器公司(National Instruments，以下简称NI公司)的并行数据采集模块PXI-4472，最高采样率为10k/s；信号调理系统采用NI公司的SCXI-1520多功能信号调理模块。理论上该系统的测量绝对误差为0.1mV，考虑到噪声干扰，实际的测量误差要大于0.1mV，一般为0.2～0.5mV。

1.3 试验方法

连续变速压颤振试验技术是在保持风洞流场Ma数不变的前提下连续增加试验速压，直至接近或达到该Ma数下模型的颤振临界点。在此过程中，流场控制系统保持流场受控，数据采集系统以一定的采样率采集应变计、加速度传感器和总静压传感器的电压信号。为了避免模型与风洞试验设备因模型发生颤振而损坏，试验中采取了计算机程控关车与人工监视关车2种方式来实现风洞“紧急关车”。

吹风结束后，可视具体情况来确定颤振临界速压。若吹风速压仅达到颤振亚临界范围，则需要通过外插获取该Ma数下的颤振临界速压；若试验时直接吹到了颤振临界点，则无需再进行外插计算。

2 关键技术及解决措施

高速风洞颤振试验的关键技术主要包含4个方面：(1)颤振模型研制；(2)定Ma数变速压流场控制；(3)颤振试验数据处理；(4)颤振模型与试验设备防护。对于连续变速压颤振试验来说，上述的(1)、(4)点与阶梯变速压颤振试验是一致的，详情可参考文献[8]，本文主要针对第(2)、(3)点进行分析和说明。

2.1 流场控制

FL-26风洞用于流场建立的控制系统包括主引射器调压阀控制系统、主排气阀稳定段总压控制系统、栅指Ma数控制系统、驻室流量阀Ma数控制系统和驻室引射器调压阀控制系统。受风洞闭合回路的影响，风洞稳定段总压和试验段Ma数可表示为：

(1)

式中：p0为稳定段总压，ps为稳定段静压，Ma为试验段马赫数，py为主引射器引射压力，Sfig为栅指位移，SZL为驻室流量阀位移；pfy为辅引射器引射压力，SME为主排位移。从式(1)可以看出，2.4m风洞是一个多输入两输出的多变量控制系统[9]。

根据FL-26风洞的特点，我们设计了基于运动函数的定Ma数线性变总压控制策略。通过对Ma数的闭环调节，确保了Ma数的控制精度。具体做法是：起动风洞，建立流场到起始总压p1，然后以一定的总压变化率V来给定总压的值，待到达目标总压p2后，保持总压的调节状态，如图2所示，其运动函数如式(2)所示。在总压的线性变化过程中，由于设定的总压与反馈总压之间的偏差通常比较小，通过整定PID参数就可以确保在设定值附近具有良好的调节效果。同时，Ma数在该阶段始终处于闭环调节状态，从而可确保Ma数的调节精度。

(2)

图2 定Ma数连续变总压示意图

Fig.2 Sketch of continuously adjusting total pressure at fixing Mach number

2.2 数据处理

颤振试验数据处理的目的是获取颤振亚临界范围的模态参数或特征变量，根据振动系统稳定性原理或速压与振动能量的关系构造稳定性判据，进而外插获取颤振临界点。本文发展的连续变速压颤振试验数据处理方法分为以下3个步骤：

(1) 数据预处理。连续变速压颤振试验数据的模态参数是连续变化的。因此，在计算数据选取时，既不是分段截取(见图3(a))，也不是连续整段全选，而是采用前后搭接分段截取的方式(见图3(b))，也就是说用于计算的每段数据都具有一定量的重叠，计算后一段的参数时也用到了前面的数据信息。这样一来，既可以增加计算的样本量，保证结果具有较高的精度，又能反映出系统的时变特性[9]。

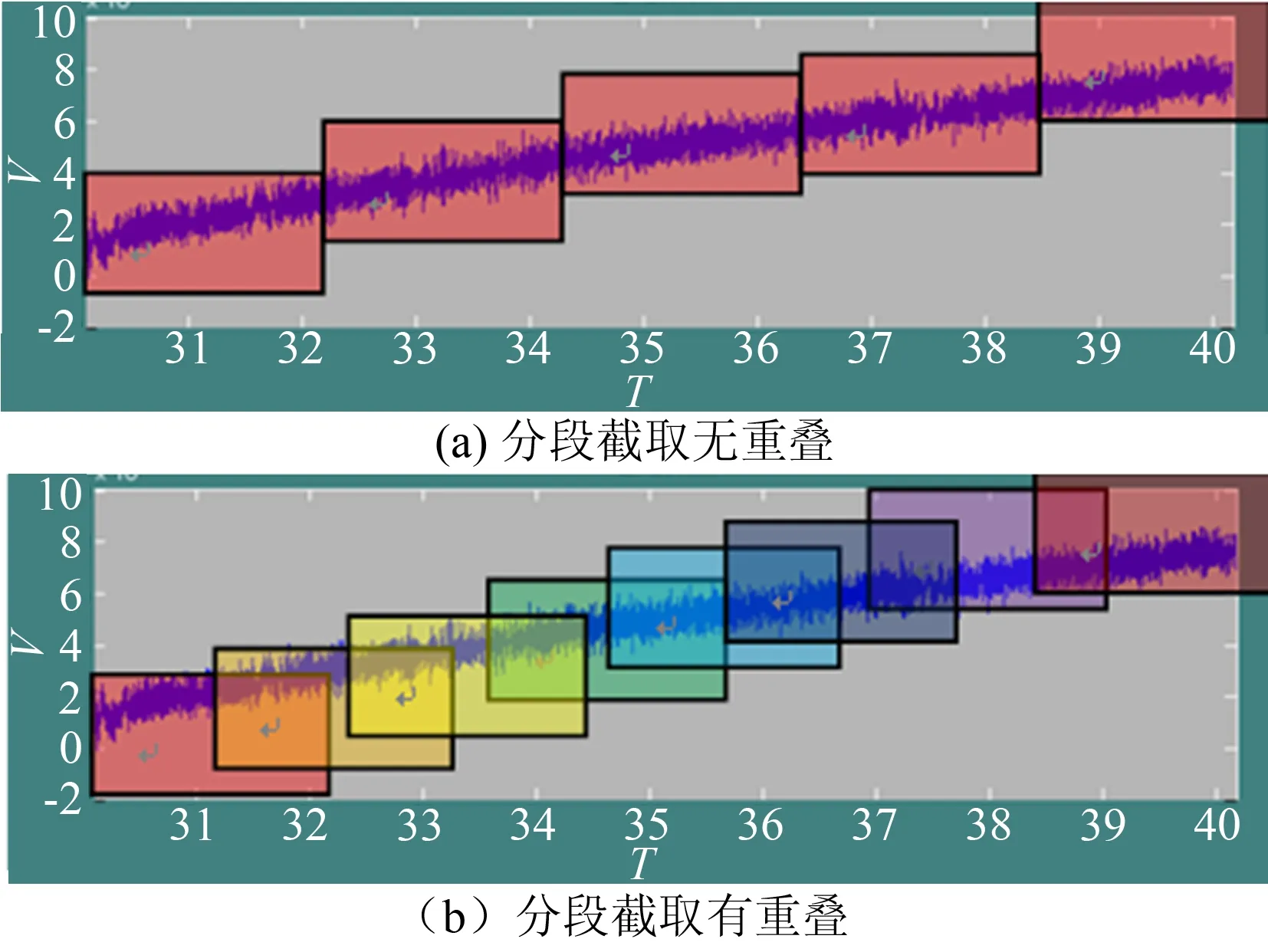
图3 数据选取策略

(2) 颤振边界的稳定性参数构造。能够用于指示颤振临界点的稳定性参数有很多，比如阻尼比、Routh判据和Jury判据等等[10]。通过实践应用证明，NASA发展的Pick-Hold方法具有较高的鲁棒性和可靠性。下文简单描述其原理：

当处于气流中的弹性系统(例如机翼)受到紊流激励时，对于系统的振幅A来说，可以用一个简单的表达式来描述：

(3)

式中：Q是广义气动力，它是马赫数与简缩频率的函数；V是气流速度；ρ是气流密度；下标f、t分别代指颤振与紊流。等式两边分别取倒数得到：

(4)

(3) 外插颤振临界点。表面上看，峰值倒数呈随机分布，但实际上可近似认为是正态分布的。于是，基于数理统计理论，将峰值倒数与其平均值的偏差作为随机变量，设定该正态分布的置信区间，摈弃置信区间以外散布度较大的数据，再次拟合峰值倒数随速压变化的曲线。若数据散布度仍较大，可重复以上步骤直至合理为止。最后，根据拟合曲线外插即可获取颤振临界速压。

3 风洞试验验证

3.1 流场调试结果分析

连续变速压颤振试验流场控制技术要求如下：

(1)Ma数变化平稳，波动量小，σM<0.005；

(2) 单车次总压跨度可达150kPa以上，使模型能从较弱的平稳振动过渡到较剧烈的亚临界振动，为亚临界预测提供所需的数据样本；

(3) 在起动过程中，速压缓慢平滑上升；关车时，速压迅速降低至0；

(4) 流场建立后，速压线性匀速爬升，且变化率可调；速压超调量尽可能小，σq<0.1kPa。

图4给出了FL-26风洞连续变速压工况时的典型流场参数控制结果，图中阴影部分曲线是流场正式建立后的区域。为了指示出试验数据的有效范围，流场控制时将在流场稳定与关车前都给出判稳信号。可以看出，在吹风过程中，速压曲线规律性较好，速压线性匀速增大，没有超调情况出现；Ma数控制平稳，曲线的波动量很小，σM<0.003，达到了期望的流场技术指标要求。

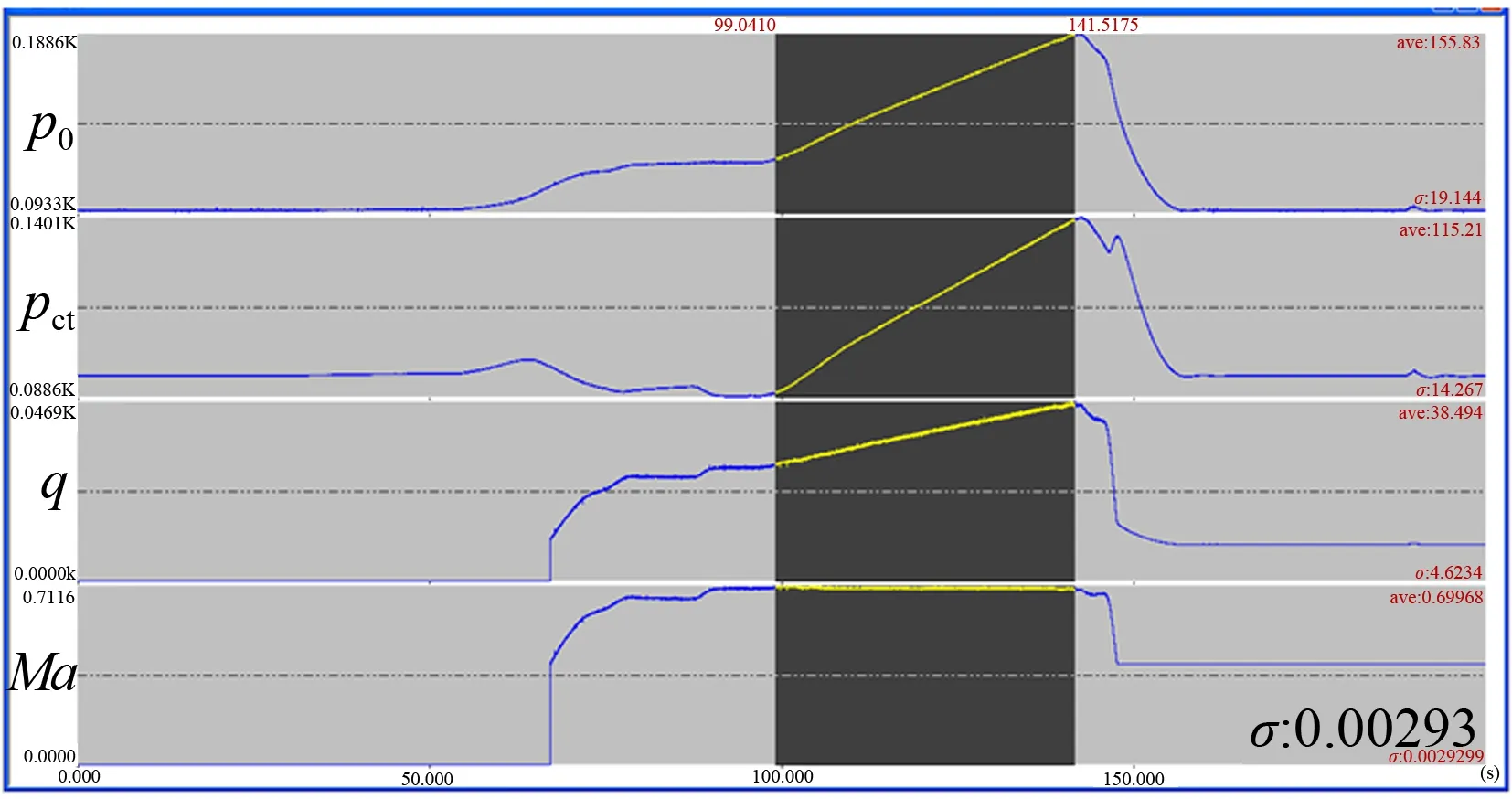
图4 典型Ma数的连续变速压流场调试结果

Fig.4 Flow field test data of continuously adjusting dynamic pressure at typical Mach number

3.2 颤振试验结果分析

(1) 阶梯与连续变速压试验结果的对比

图5给出了FL-26风洞大展弦比超临界机翼连续与阶梯变速压颤振试验工况下典型试验车次的颤振边界亚临界预测对比结果。

可以看出，在对应的有效速压范围内，2种工况下的峰值倒数变化趋势是一致的，线性拟合外插的结果相差不大。总体来看，阶梯试验结果的规律性相对更好一些，连续试验结果的数据点更多，信息量相对更丰富，且随着速压逐渐进入颤振亚临界范围，峰值倒数的散布度逐渐减小，规律性也变得更好。因此，连续试验结果峰值倒数的数据点反映了模型颤振特性随速压的变化趋势，可以给出与阶梯试验本质上一致的结果。

(2) 速压变化率对试验结果的影响

在确保试验安全的前提下，为了缩短吹风时间，减少耗气量，颤振试验时希望速压变化率尽可能大。为了验证速压变化率对试验结果的影响，图6给出了不同速压变化率情况下的颤振边界亚临界预测结果。

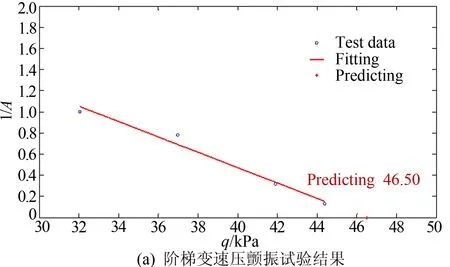
图5 阶梯与连续变速压试验结果的对比(Ma=0.7)

Fig.5 Comparison of test results with adjusting dynamic pressure on step and continuation (Ma=0.7)

图6 速压变化率影响(Ma=0.76)

从理论上来说，只要试验速压进入了颤振亚临界范围，速压变化率对预测结果的影响会很小。从图6可以看出，实际情况也与理论相符，图6中(a)与(b)的变化趋势一致，偏差小于1.4%。其中，速压变化率较大时的颤振临界速压略有降低。不难理解，当速压变化较快时，流固耦合作用更强，模型振动更加剧烈，可能导致颤振提前发生。因此，出于安全角度考虑，实际吹风时的速压变化率不宜过大。

(3) 吹风逼近程度对预测结果的影响

在高速风洞颤振试验过程中，为了避免发生颤振损坏模型及风洞设备，当试验速压接近颤振临界点时，一般希望尽早关车。但是，从预测准确性的角度来说，又要求试验速压尽可能趋近颤振临界点。这2者的要求是相互矛盾的。因此，为了同时确保试验的安全与结果的可靠，在实践中是要求试验速压必须进入颤振亚临界范围但又不能达到颤振临界点。然而，在试验前，即使是颤振亚临界范围，也是难以准确获知的，只能根据模型的设计结果来预估。因此，若要可靠地预测颤振临界点，数据处理方法就不应该对试验速压的逼近程度过于敏感，否则，亚临界预测便失去了应有的意义。为了检验数据处理方法的鲁棒性，利用同一试验车次的不同速压段分别进行计算，图7给出了相应的计算结果(qM表示每车次试验过程中吹风速压的最大值)。可以看出，尽管图中所示的试验速压逼近程度不一样，但是最终的预测结果在规律性和数值上是基本一致的。

图7 试验速压逼近程度对结果的影响(Ma=0.7)

3.3 连续与阶梯试验的耗气量对比

对于高速暂冲式风洞来说，采用传统的阶梯变速压颤振试验方法，其耗气量是惊人的，通常数10倍于常规测力测压试验。发展连续变速压颤振试验技术的主要目的之一就是节省耗气量，下文通过对比分析来说明其效果。图8给出了典型状态下阶梯与连续变速压颤振试验工况下的流场参数变化情况，同时也反映了其各自的耗气量情况。根据计算，在Ma=0.7时，为了获取研究模型的颤振点，阶梯变速压颤振试验工况下的耗气量为3.05pA(pA表示气源系统的压力降低1个大气压时所对应的耗气量)，连续变速压颤振试验工况下的耗气量为1.87pA，节省耗气量将近40%。对于大型跨声速风洞来说，其经济性可见一斑。这主要是由于连续试验工况没有了中间的速压阶梯，在相同的速压范围内，吹风时间缩短，总耗气量必定减少。

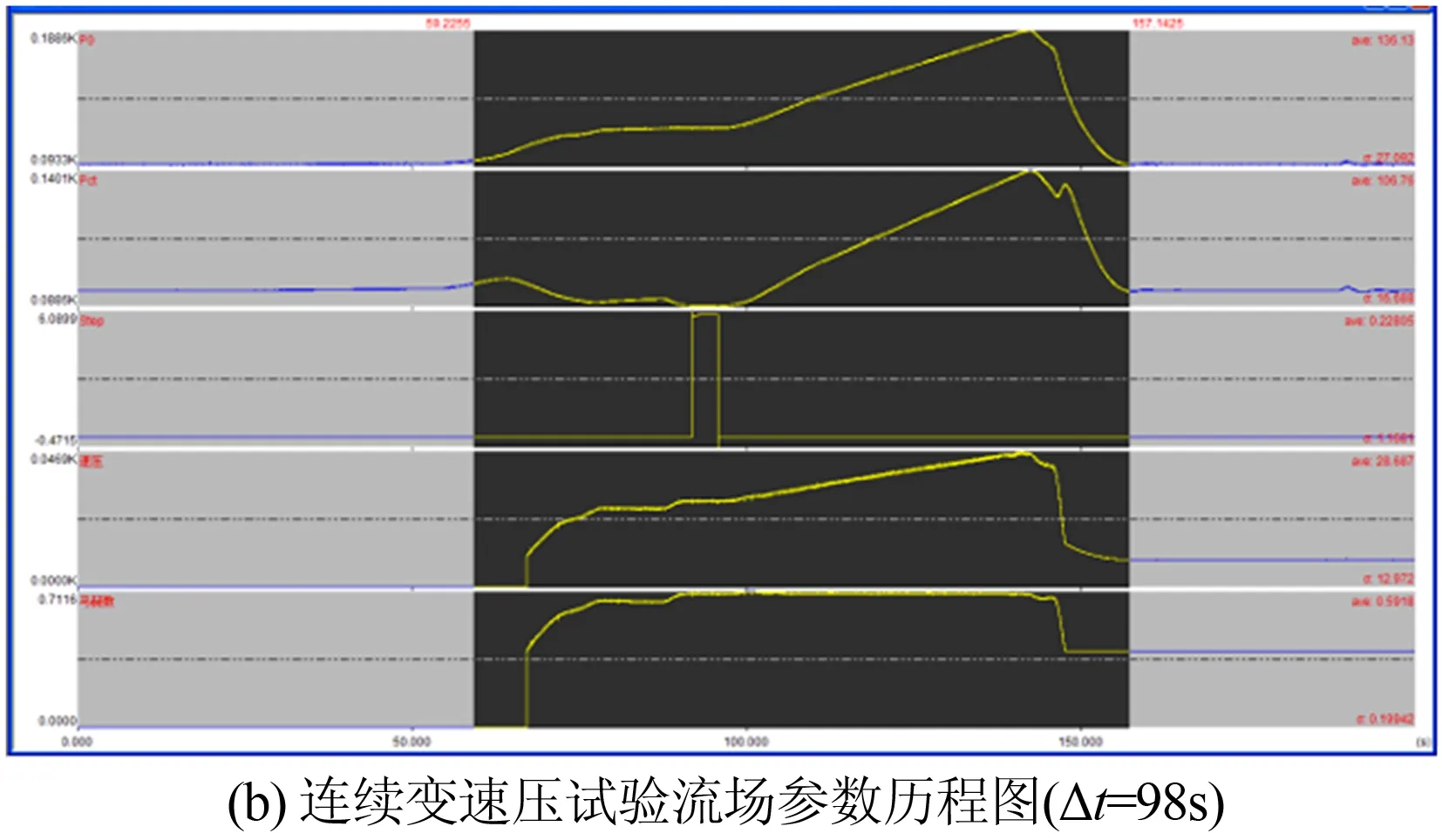
图8 2.4m风洞阶梯与连续变速压试验的耗气量对比(Ma=0.7)

Fig.8 Comparison of gas consumption in 2.4m wind tunnel with adjusting dynamic pressure on step and continuation

4 结 论

以FL-26跨声速风洞为研究平台，建立适用于大型高速暂冲式风洞工程实用的连续变速压颤振试验技术，使用大展弦比超临界机翼颤振模型进行了实际考核验证，并对试验结果进行了对比分析。得到了以下结论：

(1) 针对FL-26风洞设计的基于运动函数的定Ma数线性变总压控制策略，实现了流场的定Ma数连续变速压控制目标，Ma数控制精度达到0.005以内，且试验过程中速压没有超调情况出现，满足了高速风洞颤振试验的技术指标要求。

(2) 采用Pick-Hold方法构建颤振边界的亚临

界预测判据，基于数理统计理论的参数估计方法来减小预测判据的散布度，从而提高颤振边界亚临界预测准确性。

(3) 在高速暂冲式风洞采用连续变速压颤振试验技术可以取得与阶梯变速压颤振试验技术一致的结果，且鲁棒性较高，具备了工程实用化水平。

(4) 在高速暂冲式风洞采用连续变速压颤振试验技术时耗气量大大降低，经济效益更加显著。

[1]Garrick I E, Reed W H. Historical Development of Aircraft Flutter[J]. Journal of Aircraft, 1981, 18(11): 981-994.

[2] Charles L Ruhlin, Judith J Watson. Evaluation of four subcritical response methods for on-line prediction of flutter onset in wind-tunnel tests[R]. AIAA 1982-82-0644: 94-101.

[3] Robert V, Doggett J. Some observations on the houbolt-rainey and peak-hold methods of flutter onset prediction[R]. NASA TM-102745, 1990: 1-10.

[4] William D Anderson. The aeroelastic design and testing of the F/A-22[C]. 2005 USAF Aircraft Structural Integrity Program Conference, Memphis, Tennessee, 2005.

[5] Torii H, Matsuzaki Y. Flutter margin evaluation in discretetime system[R]. AIAA 1998-98-1724: 229-236.

[6] Torii H, Matsuzaki Y. Application of a new aeroelastic stability criterion for real-time flutter prediction[R]. AIAA-1999-99-1351: 1314-1320.

[7] Robert Walker, Naren Gupta. Real-time flutter analysis[R]. NASA Contractor Report, 170412, 1984.

[8] 卢奇正. 风洞模型颤振试验技术[R]. CARDC-2, 1996.

[9] 郭洪涛, 刘靖, 吕彬彬, 等. 连续变速压颤振试验数据处理方法研究[C]. 第十四届系统仿真会议, 2012, 7: 888-893.

Guo Hongtao, Liu Jing, Lyu Binbin, et al. Investigation on data processing method for flutter test with continuously-varying dynamic pressure[C]. The 14th System Simulation Technology & Application, 2012, 7: 839-843.

[10] 郭洪涛, 路波, 吕彬彬, 等. 面向紊流激励响应的颤振亚临界预测方法[C]. 第十三届系统仿真会议, 2011, 8: 888-893.

Guo Hongtao, Lu Bo, Lyu Binbin, et al. A subcritical prediction of flutter onset for excitation response based on airstream turbulence[C]. The 13th System Simulation Technology & Application, 2011, 8: 888-893.

(编辑：杨 娟)

Research on flutter test technology of continuously adjusting dynamical pressure in high-speed wind tunnel

Guo Hongtao1,2,*, Yan Yu2, Yu Li2, Lyu Binbin2, Du Ning2

(1. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China; 2. High Speed Aerodynamics Research Institute, China Aerodynamics Research and Development Center, Mianyang Sichuan 622763, China)

According to the defects shown in the flutter tests of stepped adjusting dynamical pressure in high speed intermittent wind tunnel, such as: long testing time, high gas consumption, and short acceptable life of testing models, researches on flutter test technology of continuously adjusting dynamical pressure in high-speed intermittent wind tunnels are conducted. Technical problems of flutter test data processing and wind tunnel flow controlling have mainly been solved. The specific approaches are: in the 2.4m×2.4m blow off transonic wind tunnel, fixed Mach number and linear varying total pressure controlling strategies based on movement function are presented, and thus the flow controlling goal of fixed Mach number continuously adjusting dynamical pressure is achieved. The controlling uncertainty of Mach number reaches less than 0.005 without deviation of dynamical pressure. The Pick-Hold method is adopted to set up the subcritical prediction criterion in flutter boundary; according to the characteristic that the reciprocal of predicting criterion is close to the normal distribution, a parameter estimation method based on the mathematical statistics theory can be used to reduce the diffusive sampling of the prediction criterion and then the accuracy of the subcritical prediction of flutter boundary can be increased. The results of wind tunnel verification test show that the flutter test results of continuously adjusting dynamical pressure is in consistent to that of stepped adjusting dynamical pressure, and the test technology has reached engineering practical levels; besides, the gas consumption is greatly reduced by using flutter test technology of continuously adjusting dynamical pressure, and thus it also has good economic benefits.

flutter;aero-elasticity;wind tunnel test;test technology;flow controlling

1672-9897(2015)05-0072-06

10.11729/syltlx20150061

2015-04-26;

2015-06-10

GuoHT,YanY,YuL,etal.Researchonfluttertesttechnologyofcontinuouslyadjustingdynamicalpressureinhigh-speedwindtunnel.JournalofExperimentsinFluidMechanics, 2015, 29(5): 72-77. 郭洪涛, 闫 昱, 余 立, 等. 高速风洞连续变速压颤振试验技术研究. 实验流体力学, 2015, 29(5): 72-77.

V215.3+4

A

郭洪涛(1980-)，男，四川南部人，高级工程师，博士研究生。研究方向：飞行器气动弹性力学。通信地址：四川省北川县永安镇101信箱202室(622761)。E-mail：ght1998@126.com

*通信作者 E-mail: ght1998@126.com