基于压缩感知OMP改进算法的图像重构
郎利影,王 勇,李思骞
(河北工程大学 信息与电气工程学院,河北 邯郸 056038)
基于压缩感知OMP改进算法的图像重构
郎利影,王 勇,李思骞
(河北工程大学 信息与电气工程学院,河北 邯郸 056038)
正交匹配追踪(OMP)算法中迭代次数严格依赖信号的稀疏度K值,迭代次数选取适当会重构出高精确的图像,反之则会对图像重构质量造成严重影响。针对这一问题,提出了一种根据残差值的相对极差来确定最佳迭代次数的新方法。该方法要求在同一次迭代中对一幅图像的所有列同时进行迭代计算,根据极差的相对差值与门限值比较来确定最佳迭代次数,从而达到提高重构精度,消除对稀疏度K值依赖的目的。理论分析和仿真结果表明,改进的OMP算法比原有算法有更理想的重构效果,有更高的重构精度。
压缩感知;正交匹配追踪算法;OMP;信号重构
压缩感知(Compressive Sensing,CS)理论[1-2]表明,当一信号在某变换基下可稀疏变换时,则可通过采集少量投影值来实现对信号的精确重构[3]。
CS理论关键技术主要包含3项:信号的稀疏表示[4]、设计观测矩阵[5]以及对信号的重构恢复[6]。其中,信号的重构是重要组成部分。在重建算法方面,该理论自提出到现在出现了许多新的算法及改进算法。而贪婪追踪算法是一种比较经典的重建算法,其主要包括匹配追踪(Matching Pursuit,MP)[7]、正交匹配追踪(Orthogonal Matching Pursuit,OMP)[8]及其相关的一些改进算法,如正则化正交匹配追踪(Regularize Orthogo⁃nal Matching Pursuit,ROMP)[9]、子空间追踪算法(Subspace Pursuit,SP)[10]、最优正交匹配追踪(Optimized Orthogonal Matching Pursuit,OOMP)[11]等。
在OMP算法中,迭代次数严格依赖稀疏度K,理论上要求迭代次数需和原本图像的稀疏度K值相等,但现实中的稀疏度K却是未知的。若在观测端一侧增加对稀疏度的计算,则必然会加重编码段的运算负担。因此,由于无法对稀疏度进行准确测算,便无法确定合理的迭代次数,重构质量便也无法得到有效保证。
针对上述问题,提出了一种OMP改进算法,可有效解决对稀疏度的依赖,确定算法中合理的迭代次数。该方案要求在同一次迭代时对一幅图像的所有列都同时进行迭代运算,并对残差值进行极差计算,以所求相对极差值为判据,通过与设定的门限值比较来确定合理的迭代次数,从而实现图像的精确重构。
1 CS理论框架


式中:矩阵Φ为M×N维的观测矩阵。若信号x不是稀疏的,则可通过M×N的变换基ψ=[ ] ψ1,ψ2,…,ψN对其进行稀疏变换,即

式中:s是信号x在变换域ψ下的K稀疏表示。
因此,压缩感知的过程可以描述为

式中:Θ=Φψ,即传感矩阵。
由式(1)求解x显然是一个欠定问题,即无法直接从观测值y中求出x。但是在满足式(1)的所有情况中找到具有最稀疏特性的信号即为所求,问题便转换为P0求解最优l0范数问题

而对式(4)P0的求解却又是一个NP难题。但CS理论指出,如果观测矩阵Φ满足约束等距性RIP[12](Restricted Isome⁃try Proper)条件,则可高概率重构原始信号x满足
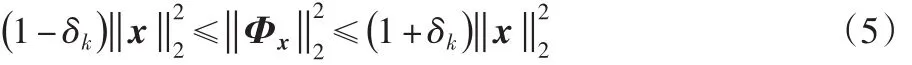
研究证明,对于时域可压缩信号,即信号x满足式(2)可进行稀疏变换,如果变换矩阵ψ与观测矩阵Φ不相关,则传感矩阵Θ=Φψ在很大概率上满足RIP性质[13]。于是可以把问题进一步转换为l1范数来求解,即转换为通过P1求解的问题

l1范数最小化问题则可使用基追踪BP(Basis Pursuit)[14]法求解,并转换为线性规划LP(Linear Programming)问题,通过凸优化算法求解。
2 OMP算法
输入:观测矩阵Φ,采样值y,稀疏度K。
输出:x的K-稀疏逼近x^。
1)令残差r0=y,索引集Λ0=∅,迭代次数t=1。
2)求残差r和传感矩阵的列φj内积中最大值所对应的脚注λ,即


4)最小二乘法求信号近似解

5)更新残差值

6)判断t>K,若满足则停止迭代;若不满足则执行步骤2)。
OMP算法运用了MP算法中的原子选择原则,但在迭代中通过递归对所选全部原子进行正交化处理,从而减小迭代次数。
3 OMP改进算法设计分析
3.1 一维信号MSE变化分析
从第2节OMP算法可知,迭代次数t的选取严格取决于原始信号的稀疏度K。而t的选取是否合适却又会对图像重构质量产生严重影响。分别对一维信号和二维图像采用高斯随机矩阵进行观测,然后采用OMP算法分别进行重构,并且测出迭代次数t与均方误差MSE(Mean Squared Error)和峰值信噪比PSNR的关系。
设其一维信号为
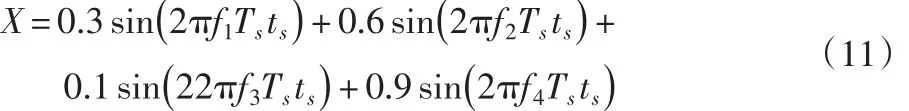
式中:信号频率 f1=50Hz,f2=100Hz,f3=200Hz,f4=400Hz;采样频率 fs=800Hz;采样间隔 ts=1/fs;采样序列Ts=1∶256。
从图1a可以看出:当迭代次数t在较小值区间时,均方误差MSE均随着t的增大而减小,相应的一维信号重构质量越来越好。当继续增大到一定程度时,MSE值保持平稳,此时的重构质量趋于稳定。但当t增大到一定数值时,MSE值骤然增大,且均产生了较大的波动,此时重构的一维信号变差。而且从图1b还可以看出,在迭代过程中,残差值的变化趋势与MSE变化趋势基本相同,且MSE值产生波动的转折点恰巧是残差值产生波动的转折点。
3.2 二维图像PSNR变化分析
实验中,再分别对纹理较复杂的Lena和纹理较简单的Flower二维图像进行迭代次数t和PSNR值变化对比实验。
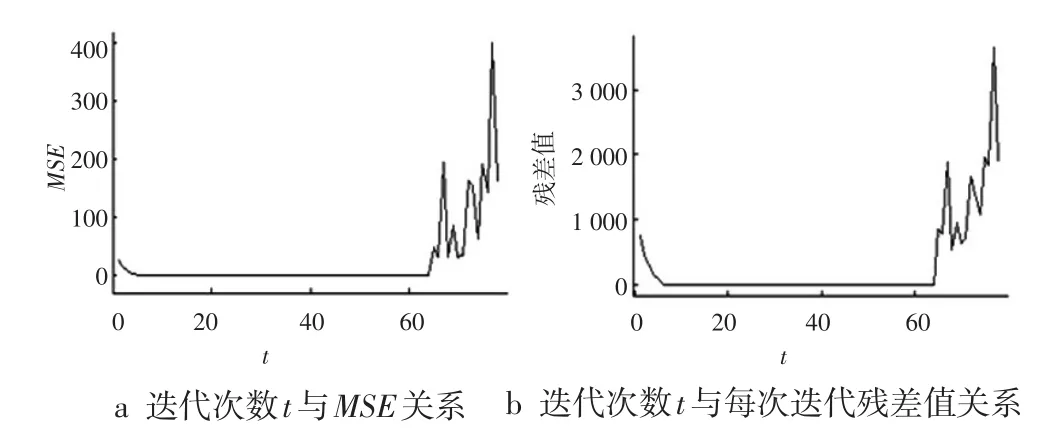
图1 一维信号迭代次数t与MSE和残差值关系
从图2b和图2d可以看出:在开始阶段PSNR增大较快,相应的重构图像质量越来越好。当t增大到一定程度时,PSNR值均趋于平缓,重构图像质量趋于稳定。但当t继续增大到一定数值时,PSNR值骤然下降,且一直保持着较低值,此时重构图像质量变得很差。

图2 不同纹理度的二维重构图像的PSNR值
3.3 本文方案设计分析
在此引入“极差”的概念,将极差定义为:在同一迭代次数t时对所有列进行残差求值,对获得的最大残差值和最小残差值之和进行平均计算。OMP算法中,每一列进行不同次数迭代的过程中残差值r是收敛减小的,故随着迭代次数的增加,在同一迭代次数下对不同列所求得的极差值也是收敛减小的。
设M×B维观测信号y,在不同的迭代过程中,对y的每一列yb运用OMP算法求得的残差值r均是收敛的,即满足

式中:rb,t和rb,t+1分别表示第t和t+1次迭代时观测信号 y的任一列yb产生的残差值。
基于此,可以推断出在第t次迭代中,同时对B列观测信号进行迭代计算,每一列求得的残差值r,必然满足

设在第t次迭代中,其B列观测信号对应的最大残差值为ϑt,最小残差值为ξt,则ϑt和ξt满足

则在第t次迭代中,B列观测值所产生的残差rb,t均介于最小残差ξt和最大残差ϑt之间,即满足

对最大残差值ϑt和最小残差值ξt之和求平均值,即求得极差Λt为

由于最大残差值ϑt和最小残差值ξt均收敛减小,故极差Λt亦收敛减小,且能够较好地反映残差值的平均变化水平。
对比图2、图3可以看出:当迭代次数t在较小区间时,PSNR值增大较快,极差值减小较快;随着t的增大,在PSNR骤然增大时,极差值骤然下降;但当t增大到一定数值,PSNR值骤然降低时,极差值亦同时骤然增大;当PSNR值在较低区间值时,极差值处在较大区间值。由此可以看出,在迭代过程中,其PSNR值的增减变化趋势与极差值的增减变化趋势密切相关,且具有相同的趋势变化转折点。
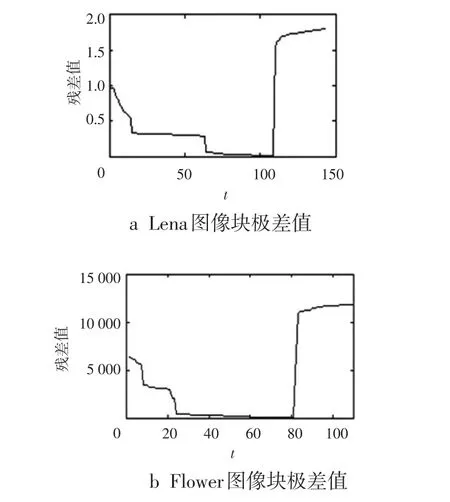
图3 不同纹理复杂度的极差值与迭代次数t的关系
为了更准确地求取PSNR增减变化的转折点,进一步求相邻两次迭代运算的极差Λt和Λt+1的相对差值为
式中:Λt和Λt+1分别表示第t次和第t+1次求得的极差值。
通过图4可以看出,在PSNR值转折点(图4a中t=110和图4b中t=81)之前,极差值d<0,且变化幅度较小;从图4c、图4d中可看出,在PSNR值转折点之后,极差值d<0,变化幅度亦较小;从图4e、图4f可看出,在PSNR值转折点之时,相对差值d产生了较大幅度的跳跃。

图4 迭代次数与相对极差值关系
于是可以通过设定一相对极差门限值,在迭代过程中其相对极差值小于此门限值时,则可认为是合理的迭代次数,此时重构出的图像质量较高,反之则是不合理的迭代次数。
3.4 OMP改进算法步骤
Φ为观测矩阵,y为M×B维采样值,x^为x的稀疏逼近。
1)令残差r0=y,索引集Λ0=∅,迭代次数t=1,采样信号y列数b=1。
2)求第t次迭代时残差r和观测矩阵的列ϕj内积中最大值,其对应的脚注λ为

3)更新索引集

记录重建原子集合

4)最小二乘法求近似解

5)更新残差值

6)判断b=B,不满足则执行步骤2);反之则执行下一步。
7)求极差

8)求相对极差值

9)与给定门限值δ比较,若dt>δ则停止迭代,输出上一次迭代求解值;若dt<δ满足,则t=t+1,并再回到步骤2)进行下一次迭代。
4 实验仿真结果
4.1 实验一:相同采样率和稀疏度时两种算法比较
为检验改进算法的重构性能,实验中,在同一采样率和相同的稀疏度时,对256×256像素大小的二维Cameraman标准图像运用快速傅里叶变换进行稀疏分解,再分别用两种算法各自进行150次重构实验,并计算测量次数变化过程中的PSNR值和重构误差率的平均值。实验中设门限值δ=5,其测试对比结果如图5、图6所示。

图5 两种重构算法PSNR值比较

图6 两种重构算法重构误差率比较
通过图5、图6可以看出,当采样率和稀疏度一定时,随着测量次数的增加重构概率均增大,重构误差率减小,但改进后的OMP算法在PSNR值和误差率上比原有算法都有了较大水平的提高,而且测量次数在小于100的范围时,OMP改进算法的优势较为凸显,当大于100时,随着测量次数的增大,OMP算法和本文算法的差距趋于减小。
4.2 实验二:相同采样率、不同稀疏度时多种重构算法比较
为了验证稀疏度的改变对此改进算法重构性能的影响,实验中,又在同一采样率下(M/N=0.6),对绝对稀疏的0-1随机信号进行采样重构,以高斯随机矩阵作为观测矩阵,稀疏度K从10开始,每次增大5,运用多种重构算法对每个稀疏度K各进行150次实验比较,并最后对其求平均值,实验中设门限值δ=5,实验结果如图7所示。
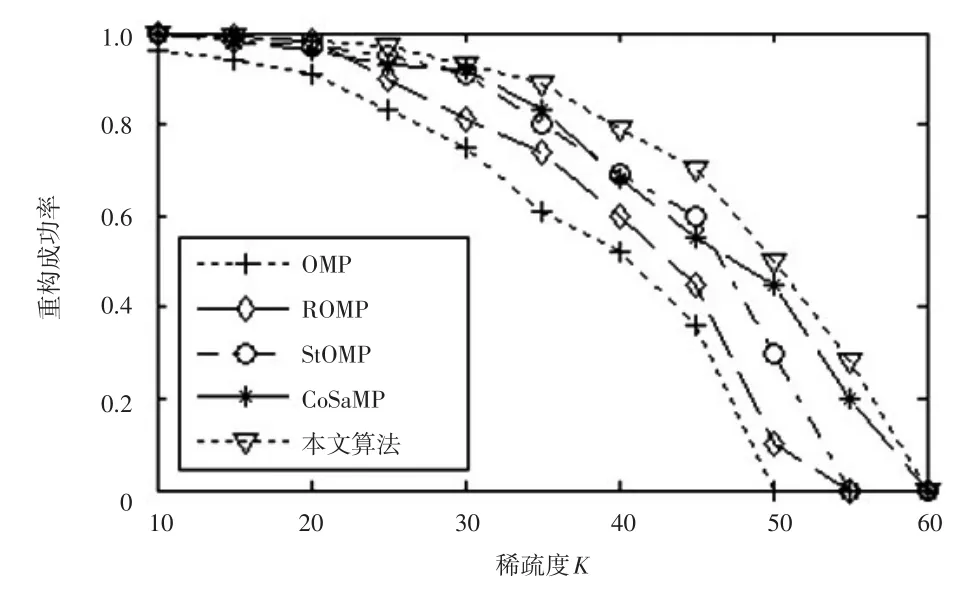
图7 改变稀疏度时各种重构算法成功率比较
由图7可以看出,当测量次数一定时,随着稀疏度的增大,各种重构算法的重构成功率逐渐减小。当信号稀疏度较大时,对比原有OMP算法本文算法有着较为明显的优势(如稀疏度K在50时)。与其他重构算法相比,本文算法在重构成功率上也有了较大程度的提高。稀疏度K在30~50之间,效果尤为明显,比其他重构算法提高了5.71%~27.53%。
4.3 实验三:相同稀疏度、不同采样率时多种重构算法效果比较
为了验证采样率的改变对改进算法重构效果的影响,实验中选用Lena标准图像进行验证。同时为了提高运算速度,运用分块压缩感知方法,先对Lena图像进行16×16的分块,再通过加权的高斯随机矩阵作观测矩阵,最后对每个图像分块进行重构恢复。
实验中分别选用不同采样率(M/N)为0.3,0.4,0.5,0.6进行测试,设其门限值δ=1,运用多种重构算法,在同一采样率下对每种算法反复进行150次试验,获得不同情形下的峰值信噪比PSNR值,并对求其平均值,其测试结果如表1所示。
通过表1可以看出,在相同稀疏度时,随着采样率的增大,各种算法的PSNR值均相应增大,且在不同采样率下OMP改进算法的PSNR值都比原OMP算法均有较大程度的提高,在较小采样率下其优势更为凸显,在采样率为0.3,0.4时分别提高了2.36 dB和2.11 dB。同时,与其他重构算法相比,本文算法的PSNR值也有了较大程度的提高。采样率在0.3~0.6间对比SAMP算法提高了1%~1.83%,对比ROMP算法提高了3.64%~6.59%,此时相应的重构效果也有了较大程度的改善。

表1 不同采样率各种算法PSNR值比较
图8是在门限值δ=10,采样率分别为0.4,0.5,0.6,0.7时,应用OMP改进算法获得的重构图像。

图8 采用OMP改进算法获得的重构图像
5 结束语
本文提出了一种OMP算法中确定合理迭代次数的新方法,通过理论验证和实验证明,该方法可有效消除迭代次数对稀疏度K值的依赖,其重构成功率和重构质量比原有OMP算法和其他重构算法均有了较大程度的提高,重构图像有了较好的改善。但该方法也存在不足之处,比如该方法会在迭代中增加一定的运算量,相应地会增大其运算复杂度,故在这方面有待进一步研究改善。
[1] DONOHO D.Compressed sensing[J].IEEE Trans.Information Theory,2006,51(4):1289-1306.
[2] CANDS E.Compressive sampling[J].Proceedings of the Interna⁃tional Congress of Mathematicians,2006(3):1433-1452.
[3] BARANIUK R.A lecture Compressive sensing[J].IEEE Signal Processing Magazine,2007,24(4):118-121.
[4] 王天荆,郑宝玉,杨震.基于自适应冗余字典的语言信号稀疏表示算法[J].电子与信息学报,2011,33(10):2372-2377.
[5] 李炳杰,吕园,叶萌,等.基于非相干准则的压缩感知观测矩阵设计的极大极小方法[J].空军工程大学学报:自然科学版,2011,12(5):81-85.
[6] 吴昊,朱杰.一种用于图像重构的新型贝叶斯压缩感知技术[J].信息技术,2012(3):98-101.
[7] MALLAT S,ZHANG Z.Matching pursuit with time-frequency dictionaries[J].IEEE Trans.Signal Processing,1993,41(12):3397-3415.
[8] TROPP J,GILBERT A.Signal recovery from random measure⁃ments via orthogonal matching pursuit[J].IEEE Trans.Informa⁃tion Theory,2007,53(12):4655-4666.
[9]NEEDELL D,VERSHYNIN R.Uniform uncertainty principle and signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J].Foundations of Computational Mathematics,2009,9(3):317-334.
[10] DAI W,MILENKOVIC O.Subspace pursuit for compressive sensing[J].IEEE Trans.Information Theory,2009,55(5):2230-2249.
[11] REBOLLO N,LOWE D.Optimized orthogonal matching pursuit approach[J].IEEE Signal Processing Letters,2002(9):137-140.
[12] CANDES E,ROMBERG J,TAO T.Robust uncertainty princi⁃ples:exact signal reconstruction from highly incomplete frequen⁃cy information[J].IEEE Trans.Information Theory,2006,52(4):489-509.
[13]TROPP J,GILBERT A C.Signal recovery from random measure⁃ments via orthogonal matching pursuit[J].IEEE Trans.Informa⁃tion Theory,2007,53(12):4655-4666.
[14]CHEN S B,DONOHO D L,SAUNDERS M A.Atomic decom⁃position by basis pursuit[J].SIAM Journal on Scientific Comput⁃ing,1998,20(1):33-61.
Image Reconstruction Based on Improved OMP Algorithm in Compressive Sensing
LANG Liying,WANG Yong,LI Siqian
(College of Information and Electrical Engineering,Hebei University of Engineering,Hebei Handan 056038,China)
The iterative number of Orthogonal Matching Pursuit(OMP)algorithm strictly dependents on the signal sparsity K,and an image can be reconstructed with high precision if the number of iteration is appropriate,on the contrary may severely reduce the quality of the reconstructed image.To solve this problem,a new method is proposed to determine the optimal number of iteration which bases on the relative extreme difference of the residual value.In this method,all the columns of an image is required to iterative calculation simultaneously at the same iteration.The optimal number of iteration is determined by comparing the relative difference and the threshold value,so that the reconstruction accuracy can be improved,and the dependence on the sparsity of K can be eliminated.Theoretical analysis and simulation results show that this improved OMP algorithm not only has better results than the original algorithm in reconstruction,but also has higher reconstruction accuracy.
compressive sensing(CS);orthogonal matching pursuit algorithm;OMP;signal reconstruction
TN911.73 文献标志码:A DOI:10.16280/j.videoe.2015.06.003
【本文献信息】郎利影,王勇,李思骞.基于压缩感知OMP改进算法的图像重构[J].电视技术,2015,39(6).
河北省自然科学基金项目(F2014402094)
郎利影(1974—),女,博士,教授,硕士生导师,研究方向为人脸识别、模式识别、人工智能;
王 勇(1987—),硕士生,研究方向为模式识别;
李思骞(1989—),女,硕士生,研究方向为人工智能。
时 雯
2014-06-30

