中考数学填空题解答技巧
刘顿


填空题和选择题一样都属小题,要求每题尽可能在短时间内作答,因而可加大中考试卷卷面的知识容量,同时也可以考查同学们对数学概念的理解、数量问题的计算解决能力和推理论证能力.一般来讲,每道题都应力争在3分钟内完成.填空题只要求填写结果,每道题填对了得满分,填错了得零分.
解答填空题的基本要求是:正确、迅速、合理、简捷.解题的基本策略是:巧做.解题的要领:快——运算要快,力戒小题大做;稳——变形要稳,不可操之过急;全——答案要全,力避残缺不齐;活——解题要活,不要生搬硬套;细——审题要细,不能粗心大意.
由此,在填空题上失分一般比选择题和解答题严重,结合这种现象,我们很有必要探讨填空题的解答策略和方法.
直接法是解填空题的基本方法,它是直接从题设条件出发,通过变形、推理、运算等过程,直接得到结果.它是解填空题的最基本、最常用的方法.使用直接法解填空题,要善于通过现象看本质,熟练应用解方程和解不等式的方法,自觉地、有意识地采取灵活、简捷的解法.
例1 (2014年浙江省湖州卷)计算:50°-15°30′=______.
分析 根据度化成分乘以60,可得度分的表示方法,根据同单位的相减,可得答案.
解 50°-15°30′=49°60′-15°30′=34°30′,故答案为:34°30′.
说明 此类题是进行度、分、秒的加法计算,相对比较简单,注意以60为进制即可.
定义法是运用数学中的相关定义、概念、定理、公理等内容,作出正确解答的一种方法.
例2 (2014年湖南省长沙卷)抛物线y=3(x-2)2+5的顶点坐标是___________.
分析 由于已知抛物线的解析式是顶点式,所以可以直接写出结论.
解 依题意,得抛物线y=3(x-2)2+5的顶点坐标是(2,5).
当填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值,而已知条件中含有某些不确定的量时,可以将题中变化的不定量选取一些符合条件的恰当特殊值,或特殊角、图形特殊位置、特殊点等进行处理,从而得出探求的结论,这样可大大地简化推理、运算的过程.
例3 (2014年贵州省贵阳卷)若m+n=0,则2m+2n+1=______.
分析 由于m+n=0,于是可以设m=1,n=-1,代入计算即可.
解 ∵ m+n=0,∴设m=1,n=-1,当m=1,n=-1时,2m+2n+1=2×1+2×(-1)+1=1.即结果为1.
说明 本题的条件为m+n=0,即m与n是一对相反数,所以在取特殊值代入计算时,只要满足所取的两个数是一对相反数即可.
“数缺形时少直观,形缺数时难入微.”数学中大量数与形的问题后面都隐含着形的信息,图形的特征上也体现着数的关系.我们要将抽象、复杂的数量关系,通过形的形象、直观揭示出来,以达到“形帮数”的目的;同时我们又要运用数的规律、数值的计算,来寻找处理形的方法,来达到“数促形”的目的.对于一些含有几何背景的填空题,若能数中思形,以形助数,则往往可以简捷地解决问题,得出正确的结果.
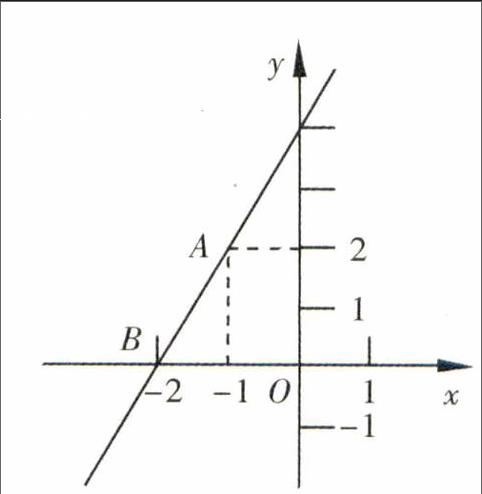
例4 (2014年湖北省鄂州卷)如图,直线y=kx+b过A(-1,2)、B(-2,0)两点,则0≤kx+b≤-2x的解集为______.
分析 观察图象,利用一次函数的性质直接确定不等式的解集.
解 根据题意可知,直线y=-2x过点(-1, 2),结合函数的图象可知,0≤kx+b≤-2x所对应的自变量的取值范围是-2≤x≤-1,即0≤kx+b≤-2x的解集为-2≤x≤-1.
说明 一方面,利用一次函数的图象与性质确定不等式解集的关键是要能正确理解图象的意义,准确地从函数图象中捕捉求解的信息;另一方面,有关不等式与函数结合的试题大致有两种情形:一是通过函数图象,利用不等式比较大小;二是利用不等式与函数结合确定最优方案和最值问题.另外,本题也可以先通过待定系数法求出一次函数的解析式,进而通过图象求解.
转化法是通过“化复杂为简单,化陌生为熟悉”,将问题等价地转化成便于解决的问题,从而得出正确的结果.
例5 (2014年江苏省无锡卷)如图,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙A和⊙B的动点,则PE+PF的最小值是______.
分析 为了方便求解,可将求PE+PF的最小值转化为基本图形与常见问题来处理,即在直线CD的同一侧,有两个定点A、B,试在直线CD上找一点P,使PA+PB的值最小.
解 连结BF、AE,则BF=1、AE=2.将求“PE+PF的最小值”转化为求“PE+2+PF+1的最小值”,即转化为在如图1中求“PA+PB的最小值”,此时出现了基本图形与常见问题:在直线CD的同一侧,有两个定点A、B,试在直线CD上找一点P,使PA+PB的值最小.如图2,过点A作关于直线CD的对称点A′,连结A′B,交直线CD与点P,则P与D重合,CD⊥AA′,PA=PA′,此时PA+PB的最小值为线段A′B的值.在菱形ABCD中,AB∥CD,∠BAD=60°,∴∠BAA′=90°,∠A′=30°,因此A′B=2AB=6.即如图1中PA+PB的最小值为6,从而PE+PF的最小值为6-3=3.
说明 现阶段我们求线段和的最小值的常见题型:(1)两点在一条直线两侧;(2)两点在一条直线同侧(涉及一次轴对称);(3)一点在两相交直线内部(涉及二次轴对称);(4)两点在两相交直线内部(涉及二次轴对称).解答以上最值问题的基本原理:①两点之间线段最短;②垂线段最短.
近年来的中考试卷中频频出现一些规律探究型的填空题,此类题一般都具有一定的难度,要求同学们善于分析题意,并通过归纳、猜想、验证,从而得到结果.
例6 (2014年江苏省盐城卷)如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1,S2,S3,…,Sn,则Sn的值为___(用含n的代数式表示,n为正整数).
分析 根据直线解析式判断出直线与x轴的夹角为45°,从而得到直线与正方形的边围成的三角形是等腰直角三角形,再根据点A的坐标求出正方形的边长并得到变化规律表示出第n个正方形的边长,然后根据阴影部分的面积等于一个等腰直角三角形的面积加上梯形的面积再减去一个直角三角形的面积列式求解并根据结果的规律解答即可.
说明 本题考查了正方形的性质、三角形的面积、一次函数图象上点的坐标特征,依次求出各正方形的边长是解题的关键,难点在于求出阴影Sn所在的正方形和正方形的边长.
(编辑 孙世奇)

