大中见小 小中见微 微中见效

赵立新

[摘 要] 江苏中考连云港卷第27题源于教材又异于教材，依据教材又高于教材，从学生熟悉、简单的数学模型、问题出发，低起点、循序渐进地给考生信心，通过问题串逐步变式，对问题的研究进行纵向深化和横向推广，同时也给考生指引了解题方向，使研究方向不断向前发展，从而得到更深刻或更普遍的新结论，向问题的本质特征不断靠拢.

[关键词] 大中见小；小中见微；微中见效；数学模型；问题串

某数学兴趣小组对线段上的动点问题进行探究，已知AB=8.

问题思考？摇 如图1所示，点P为线段AB上的一个动点，分别以AP，BP为边在同侧作正方形APDC和正方形BPEF.

（1）当点P运动时，这两个正方形的面积之和是定值吗？若是，请求出；若不是，请求出这两个正方形面积之和的最小值.

（2）分别连结AD，DF，AF，AF交DP于点K，当点P运动时，在△APK，△ADK，△DFK中，是否存在两个面积始终相等的三角形？请说明理由.

■

问题拓展？摇 （3）如图2所示，以AB为边作正方形ABCD，动点P，Q在正方形ABCD的边上运动，且PQ=8. 若点P从点A出发，沿A→B→C→D的线路向点D运动，求点P从点A到点D的运动过程中，PQ的中点O所经过的路径的长.

■

（4）如图3所示，在“问题思考”中，若点M，N是线段AB上的两点，且AM=BN=1，点G，H分别是CD，EF的中点，请直接写出点P从M到N的运动过程中，GH的中点O所经过的路径的长及OM+OB的最小值.

■

作为中考数学压轴题，所涉及的知识点多、覆盖面广、条件隐蔽、关系复杂，其主要功能是对学生的学习水平进行区分，考查学生对初中数学核心知识和重要思想方法的理解和掌握水平，为高中学校的招生提供依据. 所以，作为一道压轴题，如何能“压”到“轴”上，才是关键.

特色1：大中见小，似曾相识

作为一道大题，从中可以找到学生们熟悉的基本图形或模型.

模型1：面积最值问题

在教材中我们常见的是把一段铁丝折成两段，围成两个正方形，如何折才能使它们的面积之和最大，考查的是二次函数的基本性质（最值问题）. 本题的问题（1）是求以折成的两段为边长的两个正方形的面积之和的最值，很多考生知道这个结论，再借助数形结合，给出严谨的演绎推理，便能证明判断的正确性.

模型2：面积相等问题

在平时的练习中，对于正方形我们常见的面积相等问题是转化为同底等高或等底等高或等底同高，如图4所示，有三个正方形ABCD，BEFG，RKPF，点G在线段DK上，正方形BEFG的边长为4，则△DEK的面积为多少？该题只要连结三条对角线DB，GE，FK（如图5），分别把阴影部分△GDE，△GKE的面积转化为△GBE，△GFE的面积，它们的和即为正方形BEFG的面积16. 而问题（2）中寻找面积相等的两个三角形，我们同样可以连结对角线PF（如图6），得△APF，△DPF的面积相等，从而得到△APK，△DKF的面积始终相等，或者从梯形APFD的角度易得△AKP与△DKF的面积相等.

■

■

■

模型3：距离最短问题

在距离之和最短问题中，常见的是这样一个题：如图7所示，直线m表示一条河，M，N表示两个村庄，欲在m上的某处修建一个送水站，向两个村庄供水，选在何处使得到两个村庄铺设的管道最短？我们只需作点M关于直线m的对称点P，再连结NP，交直线m于点O，点O即为所求（如图8）. 而本题的问题（4）中求OM+OB的最小值，和它如出一辙.

依据教材，推陈出新，源自“相似”又高于“相似”，似曾相识又有所不同，把学生常见的数学模型有机地整合到一起，梯度设置合理，使得该题构思精巧、不落俗套，学生在熟悉的背景中解题，有一种自然地亲切感，也培养了学生的数学素养与图形感知.

特色2：小中见微，拓展能力

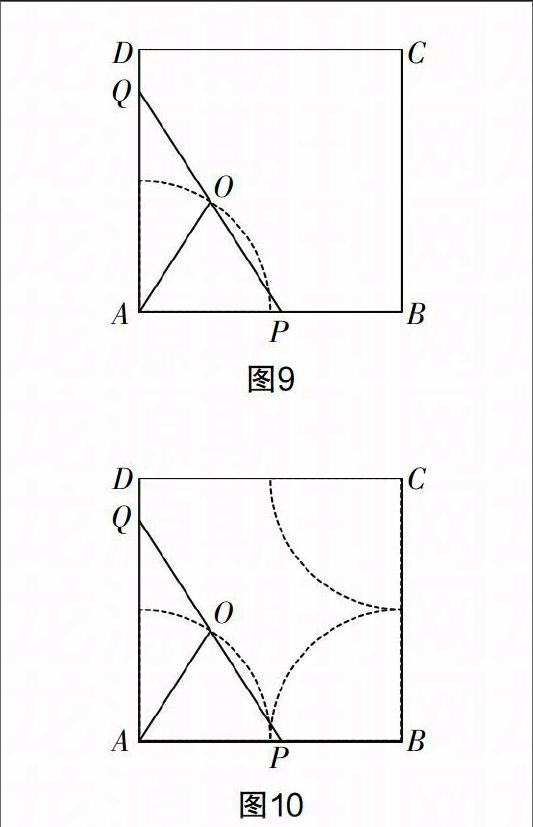
动点问题一直是数学教学的难点，如何理清“动”与“静”的辩证关系，是解决其运动轨迹的关键. 本题的问题（3）是求PQ的中点O所经过的路径的长，任何运动中或多或少存在着“数”或“形”的关系和不变性，学生首先会从形上感受其特点，但很难有所收获，进而学生会从“数”上寻求突破. 当点P在AB上运动时，抓住PQ是定长8的特点，运动的中点O因为是斜边PQ的中点，所以可以得到AO=■PQ=4，也就是说，当点P在AB上运动的过程中，AO的长度始终保持不变，实际上就形成了一段弧（如图9），以此类推，当点P从点A出发，沿A→B→C→D的线路向点D运动时，点O的轨迹应该是三段一样的弧（如图10），所以路径总长为6π.

■

■

运动是相对的，运动又是有关联的，形动可由点观，点动可由形察，本题既考查学生的观察能力，又考查学生的分类思想，以及平时积累的数学探究经验等，还渗透了对转化、数形结合等数学思想的考查. 解答本题，要求学生具有较好的空间与图形素质、基本运算能力，以及综合运用所学知识分析问题、解决问题的能力，试题突出了能力立意的特点.

特色3：微中见效，提升思维

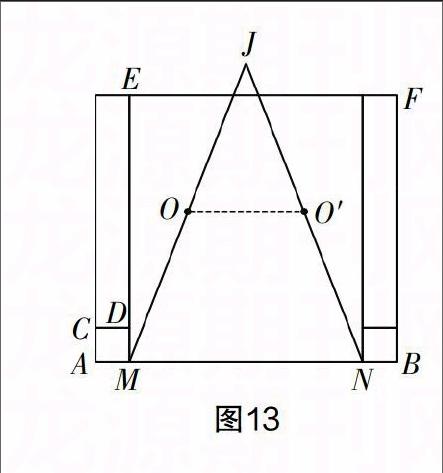
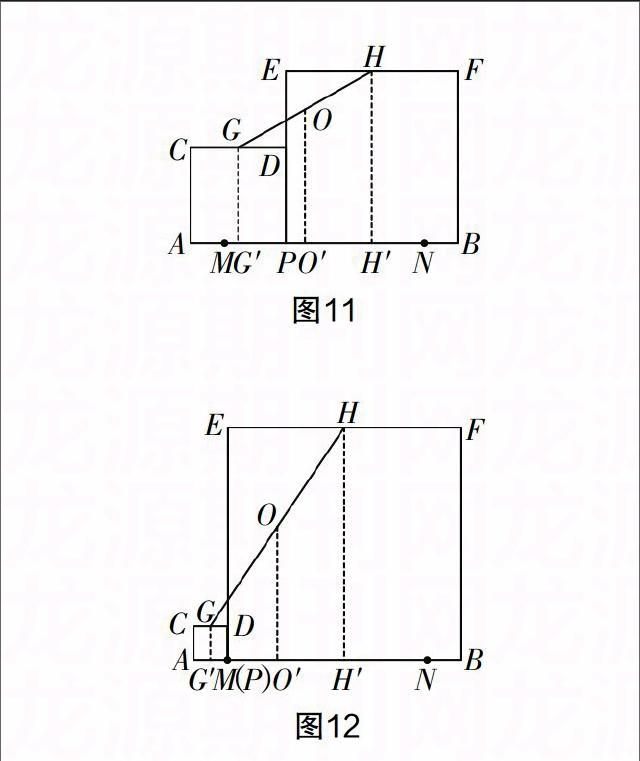
如果说问题（3）是考查学生的能力，那么问题（4）的出现对学生数学思维的考查已经远远超出知识本身. 首先，学生在问题（3）的探究中初步具备了寻求动点轨迹的基本方法和一般步骤，而问题（4）与问题（3）具有相同的地方是AB为8，不同的是当点P在线段MN上运动时，左、右两个正方形是变化的，那么它们的边CD，EF的中点G，H也是变化的，所以GH的中点O所经过的路径是什么就变得扑朔迷离. 此时对学生数学素养的要求就更高了，既要从多点的变化中寻找点O的轨迹，又要转化为与已知数量有关联的结论，所以要求学生有较高的数学思维能力. 可抓住点O是GH的中点这个条件，构造梯形的中位线或全等三角形. 如图11所示，过点G，O，H分别作AB的垂线G G′，OO′，HH′，垂足分别为G′，O′，H′，则可得到OO′=■（GG′+ HH′）=■（PA+ PB）=■×8=4，说明点O到AB的距离始终为4，进而得到点O运动的轨迹为平行于直线AB且到它的距离为4的一条直线. 当点P从点M到点N运动的过程中，点O运动的轨迹即为一条线段. 由问题（3）的曲线（圆弧）到问题（4）的直线（线段），要依靠学生具有的较强迁移能力和构造、创新能力. 当点P与点M重合时，如图12所示，易得G′H′=4，则G′O′=2，所以AO′=2.5. 依据对称性可得，当点P与点N重合时，过点O作直线AB的垂线OO′，点B到垂线OO′的距离同样也是2.5，所以GH的中点O所经过的路径的长为8-2.5×2=3. 当然，为了寻求更一般的情况，我们可以借助全等三角形等知识证明点O所经过的轨迹实际上就是△JMN的中位线（如图13，由于篇幅限制，不再赘述），易求得中点O所经过的路径的长为■MN=3.

■

本题源于教材又异于教材，依据教材又高于教材，从学生熟悉、简单的数学模型、问题出发，低起点、循序渐进地给考生信心，通过问题串逐步变式，对问题的研究进行纵向深化和横向推广，同时也给考生指引了解题方向，使研究方向不断向前发展，从而得到更深刻或更普遍的新结论，向问题的本质特征不断靠拢. 所以该题依据学情，有针对性，有目的性，具有较强的诊断、反馈、选拔功能，有利于改进教学，提高效果.endprint