数学图式：开启数学教学的“金钥匙”

郭海燕

[摘 要] “数学图式”将抽象的数学概念形象化、复杂的数学计算简约化、孤立的知识点结构化，体现了操作性强、理解性好的特质. 不仅如此，“数学图式”的衍生还与儿童的思维特质高度吻合，给了儿童具体的思维支撑、想象支撑、问题解决支撑.

[关键词] 小学数学；数学图式；帮助

“数学图式”是由数学符号、数学图象信息、数学示意图等构成的具有解释意义和解释框架的数学认识组块或模式. 数学图式往往兼有形象与抽象的双重表征和特质. 一方面，数学图式建基于儿童的已有知识经验；另一方面，数学图式指向数学的新知识建构. “数学图式”对于培养儿童的数学化能力（数学理解、数学分析、模型化等）具有重要的意义，对于让抽象的数学概念形象化也有着重要的作用. 可以说，数学图式是开启儿童数学学习的“金钥匙”！

“数学图式”在儿童数学教学

中的意义

1. 儿童的思维发展意义

儿童的思维是从动作思维向形象思维再向抽象思维进行逐步发展提高的. 在小学阶段，儿童的思维表征主要为半形象半抽象的思维. “数学图式”正是“准抽象”思维的载体，兼有形象和抽象的特征. 儿童的思维处于成长和发展阶段，其思维支撑需要借助数学工具进行辅助，“数学图式”是数学工具辅助的脚手架. 例如，教学圆的半径、直径、周长和面积后，不少儿童对于r，d，C之间的关系经常混淆. 于是笔者在r和d之间建立2倍的关系，在d和C之间建立π的关系，在r和C之间建立2π的关系. 3个图式——2，π，2π，让儿童对公式之间的变形与转换有了抓手，杂乱的数学知识学习起来显得很有条理. 孩子的思维得到了有效的支撑和引导. 如此，公式转换从模糊变得清晰！

2. 数学知识的形象化意义

抽象化的数学知识容易让儿童的思维受阻，“数学图式”能够让抽象化的数学知识形象化；点状的数学知识点不容易整合，“数学图式”可以帮助儿童对数学知识进行系统建构，让儿童建立完整的意义结构，形成结构化的数学知识；数学知识作为一种“符号表征”，容易被儿童遗忘，“数学图式”却能够帮助建立稳定的数学记忆，让儿童在提取数学知识时有 “拐杖”等. “数学图式”让儿童更好地理解概念的数学本质，理解数量之间的关系，促进儿童对数学知识进行深度地知识建构，进而有效地提升儿童的数学素养. 例如，儿童对“分数的意义”的理解总是不到位，于是笔者教学时将分数的书写与分数的意义联通起来，让分母表示平均分的份数，分子表示有这样的多少份，如“二分之一”读作“二份之一”. 如此，让儿童借助“书写图式”理解了分数的本质内涵！

“数学图式”在儿童数学教学

中的运用

建构主义理论认为，儿童数学学习不是由教师或其他人传授的，而是他本人主动根据已有的数学经验、认知结构进行的一种主动建构的过程. 儿童本身具备一定的数学学习和数学认知经验，“数学图式”让儿童能够顺利地进行“同化”与“顺应”，从而让儿童能够主动地探寻“新知”.

1. 实践图式：让儿童的表象映象更深刻

数学实践是儿童认识数学概念的源泉，也是儿童形成数学表象的重要手段. 瑞士心理学家皮亚杰认为，智慧发端于操作，切断动手操作，儿童的智慧就无从谈起. 在数学教育中，教师要给儿童充分的动手操作机会，让儿童充分经历数学化活动，让儿童主动建构属于自我的数学知识. 例如，教学“长方形的面积”时，传统教法是教师让儿童肤浅地经历数学知识的操作活动，比如教师提供一种或给定一种规格的长方形，儿童动手用单位长度1厘米的正方形摆放. 从儿童的视角看，儿童完全是在经历一种“被实践”“被操作”；从数学的角度看，数学归纳应该让儿童经历不完全归纳的全过程，同时数学操作不是机械地动手实践，而应该蕴涵数学味道. 基于此，笔者给儿童提供多个结构性材料：长是3厘米、宽是2厘米的长方形；长是4厘米、宽是3厘米的长方形；长是7厘米、宽是3厘米的长方形；10个1平方厘米的小正方形. 首先，笔者让孩子们探索“长是3厘米、宽是2厘米”的长方形的面积. 由于“小正方形”的个数够用，孩子们的操作完全是摆和放，并没有多少真正的思维参与. 接着笔者让孩子们探索“长是4厘米、宽是3厘米”的长方形面积，这时小正方形不够用了，怎么办？儿童的思维有了初步介入，并且儿童对第一个实践活动进行观察、反思，观察长的个数、宽的个数与长方形面积的关系，并提出初步猜想；最后，笔者让孩子们探索“长是7厘米、宽是3厘米”的长方形的面积计算，这时孩子们纷纷提出准确的数学猜想，再通过小组合作进行验证. 孩子们自然而然地得出科学的数学结论. 如此，实践图式深深地印刻在儿童的心中. 在这里，儿童不是完成指令的“操作工”，而是有着深刻的、独特的数学猜想与验证. “操作图式”也成为一种“有意义的图式”，由此积极地建构起数学新知.

2. 图形图式：培养儿童数形结合意识和能力

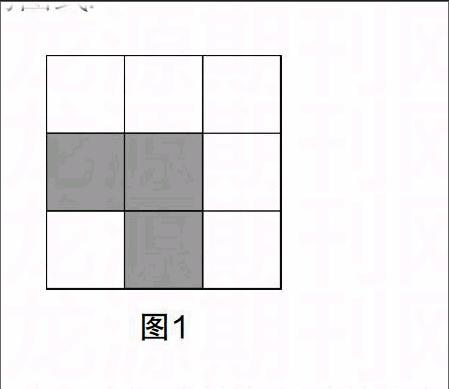
“图形图式”是图式的重要组成，是儿童进行问题解决的重要抓手. 著名数学家华罗庚曾经说过，“数形结合百般好”“数缺形时少直观”“形缺数时难入微”. 所谓“图形图式”，就是在儿童的数学学习过程中把抽象的数学符号、数量关系用直观的、形象的图形表示出来，从而“以形助数”，让抽象的数学形象化，让理性的数学问题感性化. 例如教学“解决问题的策略——转化”，对于1+3+5+7+9+11，笔者首先出示问题，孩子们纷纷动笔计算，一会儿便解决了问题；接着，笔者将问题拓展为1+3+5+…+99，激发了儿童的认知冲突；笔者适时提示孩子可以借助图形来表示，于是一些孩子画出了正方形，但孩子没有体现问题本质；接着，笔者让孩子们进行小组讨论. 于是孩子们画出如图1所示的图式.

“图形图式”让繁杂的计算变得简单，对接了儿童的形象思维与抽象思维，沟通了数与形之间的关系，凸显了数学的本质. 在接下来教学“■+■+■+■”时，儿童“见数思形”，积极主动地将这个算式与图形结合，很快便探索出把整个正方形看做“1”，平均分成2份，得到■；然后将剩下的图形也平均分成2份，得到■……最后，孩子们从“1”里减去■，得到■. 这说明，儿童的“图形图式”已经根植于思维和思想深处，成为一种解决问题的策略，同时获得了“形感”！

3. 结构图式：培养儿童灵活应用的能力

数学教材中的数学知识是按照“点”的形式呈现的，知识点之间缺少深刻的联系. 为此，教师必须有意识地引导儿童探索数学的知识结构，让儿童主动建构数学的“结构图式”，让“知识点”形成“知识链”，织成“知识网”，让独立又相互联系的知识点“图式”形成“网络结构图”，以便儿童在运用时灵活与方便地提取. 例如，教学“因数与倍数”“最大公因数与最小公倍数”时，笔者让两个跨年级的大单元知识进行知识整合，建构儿童的数学知识“结构图式”. “因数—公因数—最大公因数”“倍数—公倍数—最小公倍数”“奇数与偶数”“素数与合数”等. 明晰的“结构图式”让儿童清晰地掌握了数学知识的“来龙去脉”、数学知识的“源”与“流”，为概念的判断与问题的灵活解决奠定了坚实的基础. 再如，教学“圆的面积”后，笔者有意识地建构儿童的“结构图式”，将“长方形、正方形、平行四边形、三角形、梯形、圆形”有机地整合在一起，并且将数学思想——“转化”、图形面积的推导过程用“结构图式”表现得淋漓尽致，达到知识点之间的照应.

“数学图式”将抽象的数学概念形象化、复杂的数学计算简约化、孤立的知识点结构化，体现了操作性强、理解性好的特质. 不仅如此，“数学图式”的衍生还与儿童的思维特质高度吻合，给了儿童具体的思维支撑、想象支撑、问题解决支撑，儿童在“数学图式”的引领下，左右脑协同运作，其想象力和创造力都得到应有的系统发展. 其中，“操作图式”让儿童依靠操作活动表征数量之间的关系；“图形图式”表征着数与形之间的微妙关系；“结构图式”让儿童对数学知识进行集约化处理. 由此，儿童能够积极主动地探索数学新知，自主地经历数学知识点、知识脉络形成的全过程.endprint