基于模糊优化的原油产量分配方案分析

刘春旭　李亚蔚

[摘要] 运用回归预测和灰色预测构建操作成本三角模糊数，借鉴其他学者的油价预测研究成果得到原油价格三角模糊数，再进一步构建基于利润最大化、产量最大化和成本最小化三大目标下的模糊优化模型，利用隶属度函数进行求解，最后通过某油田分公司进行实例应用，得到不同目标条件下的最优产量分配方案。结果表明，有效的原油产量规划将提高企业利润和产量，降低成本。

[关键词] 原油产量分配；模糊优化；应用

[中图分类号]F407.22

[文献标识码]A

[文章编号] 1673-5595（2015）02-0012-07

一、引言

科学优化的产量分配计划是原油开采企业保证下一年生产、经营顺利进行的重要依据，能保证原油开采企业的总体效益达到最优。目前针对该问题的研究大多是在确定性条件下进行的，无法解决实际生产中受原油价格等外部因素影响而产生的不确定性问题。原油开采企业是根据规划年的目标，依据现有资源、国内需求量等来确定下一年本企业的总产量，并将总产量在各个采油厂或者区块间进行科学分配。

早在20世纪50年代，国外一些炼化企业就意识到对生产过程进行有效规划将给企业带来更多的利润。西蒙兹在1995年首次提出了利用线性规划来解决炼油企业规划的问题。Aronofsky等通过运用线性规划方法解决了以生产经营效益最大化为目标的生产规划问题。[1]在国内，杜军研究了当油价为确定值时油田企业如何制定最优决策的问题。[2]刘志斌和姜少慧在其文章中利用功能模拟原理建立了产量与各项开发指标之间的关联关系，并基于此建立了产量分配优化模型。[34]李博然运用免疫微粒群算法解决了原油产量分配的多目标规划问题。[5]以上研究均是基于变量全部为确定值情况下建立的，但是在原油开采和分配的过程中，存在很多不确定性因素。由于模型中原油价格、操作成本本身具有不确定性，其均是经过预测获得，不同的预测方法会导致预测结果存在差异，所以很难用一个确定的预测值来表示参数值，也就无法解决决策者允许约束条件存在弹性的问题。基于此，本文基于模糊优化进行原油产量分配优化。原油产量模糊优化是指原油产量分配过程中参数部分或者全部是不确定的，同时约束条件不一定得到严格的满足，具有一定弹性。Buckley定义了具有模糊系数的规划问题，在可能性解空间的a截集上定义了a最优规划，Julien在此模型的基础上定义了a最优规划，以提供该问题最优解的封闭区间。[6]而后Zimmermann根据模糊决策原理和线性隶属度函数将带有模糊目标和模糊约束的线性规划问题转化为确定性线性规划问题。[7]盖英杰等通过容差法将模糊线性规划问题转化为确定性的线性规划问题[8]，李孝忠等通过引入三角模糊数将具有模糊变量和模糊约束的模糊规划问题转换成多目标或者多层次的线性规划问题。[9]

二、基于模糊优化的原油产量分配决策

模糊优化是基于系数为模糊信息的条件下进行的，模糊信息是指由于事物没有清晰明确界定或者由于人们的认知范围所局限造成信息难以清晰定义的不确定性信息。产量规划过程中存在原油价格、单位操作成本等不确定性因素，所以单靠一种预测方法得到的预测值作为参数值是不科学的。本文通过不同的预测方法得到多个预测值，之后利用多个预测值构建三角模糊数，用三角模糊数体现油价和成本的变动区间，这是确定的常数无法实现的。基于模糊优化进行原油产量分配决策有四步。

（一）参数选取与处理

油田公司在安排下一年产量时，需要对原油操作成本、原油价格等主要参数进行数据的收集、处理与分析。本文主要采用实地调研法进行数据收集，以保证分配结果的准确性和科学性。为使数据具有可比性，首先对原始数据进行初步处理，例如对其进行折现处理，剔除通货膨胀等因素对走势的影响。收集到的数据资料主要有原油开采企业历年产量、固定成本、操作成本及各个采油厂或者区块的产能上下限。数据收集与初步处理完成之后，对收集到的原油价格、操作成本进行预测。

（二）原油产量分配模糊优化模型的构建

对原始数据处理完之后就是模型的构建。原油开采企业进行原油产量分配的研究大多基于利润最大化、产量最大化或者成本最小化，因此本文基于不同的目标建立利润最大化、产量最大化和成本最小化三大目标下的原油产量分配模糊优化模型。

1.利润最大化模型

建立利润最大化模型的目的是使油田年利润达到最大。油田公司的利润等于总收入减去总支出。收入主要是销售收入，销售收入=原油价格×原油产量×原油商品率；支出主要有固定成本、变动成本和税费。因固定成本不会随着产量的变化而变化，所以在做产量规划时可以将这个因素忽略，支出只包括变动成本和税费。目标函数描述如下：

π=（P-T）∑ni=1Xi-∑ni=1CiXi， i=1，2，3，…，n （1）

利润最大化的约束条件主要有：成本约束、总产量约束、决策变量约束。

中国石油大学学报（社会科学版）2015年4月

第31卷第2期刘春旭，等：基于模糊优化的原油产量分配方案分析

成本约束是指所有采油厂的总变动成本之和不能超过规定的规划年总变动成本限制，函数描述为：

∑ni=1CiXi≤C， i=1，2，3，…，n （2）

产量约束是指所有采油厂的总产量之和必须大于等于规划年规定的总产量，函数描述为：

∑ni=1Xi≥Q， i=1，2，3，…，n （3）

每个采油厂的年产量必须在采油厂年产量上下限范围内，函数描述为：

Qai≤Xi≤Qbi， i=1，2，3，…，n （4）

模糊参数有原油价格、单位操作成本，因为税费是和油价有关的，因此油价的模糊性导致税费也具有模糊性。

由式（1）、（2）、（3）、（4）得到油田利润最大化的模糊产量分配优化模型

max （-）∑ni=1Xi-∑ni=1Ci～Xi（5）

s.t∑ni=1Xi≥Q

∑ni=1Ci～Xi≤

Qai≤Xi≤Qbi， i=1，2，3，…，n

参数与符号解释见表1。

表1参数与符号解释

符号意义单位

T吨油税费元

P原油价格元

Q原油总供应量吨

C总变动成本元

Ci第i个采油厂的单位变动成本元

Xi第i个采油厂的年产量吨

Qai第i个采油厂的产量下限吨

Qbi第i个采油厂的产量上限吨

注：i=1，2，3，…，n，n代表不同的采油厂或者区块。

2.产量最大化模型

建立产量最大化模型的目的是使油田年产量最大化，油田的总产量等于各区块分配产量之和。目标函数描述如下：

Q=∑ni=1Xi， i=1，2，3，…，n （6）

产量最大化的约束条件主要有成本约束、总产量约束和决策变量约束。

据此，利润最大化的模糊产量分配优化模型为：

max ∑ni=1Xi（7）

s.t.

∑ni=1Xi≥Q

∑ni=1Ci～Xi≤C

Qai≤Xi≤Qbi， i=1，2，3，…，n

3.成本最小化模型

建立成本最小化模型的目的是使油田年总成本达到最小，这里的成本是指变动成本也是操作成本。目标函数描述如下：

C=∑ni=1CiXi， i=1，2，3…，n （8）

成本最小化约束条件与产量最大化约束条件相同，主要有成本约束、总产量约束和决策变量约束。

据此，成本最小化的模糊产量分配优化模型为：

min ∑ni=1Ci～Xi（9）

s.t.∑ni=1Xi≥Q

∑ni=1Ci～Xi≤

Qai≤Xi≤Qbi， i=1，2，3，…，n

（三）原油产量分配模糊优化模型的求解

将通过不同预测方法预测得到的参数预测值构造成三角模糊数，代入到上述不同目标条件下的分配模型中，利用隶属度函数将模型分解并进行求解，最后向油田提交不同目标条件下的最优分配方案。

以上述构建的利润最大化模型为例进行求解分析。式中、Ci～为三角模糊数，记为=（CL，CM，CR），Ci～=（CiL，CiM，CiR）。

C的隶属度函数为：

C（X）=C-CLCM-CL， CL≤C≤CM

CR-CCR-CM， CM≤C≤CR

Ci的隶属度函数为：

Ci（X）= Ci-（Ci）L（Ci）M-（Ci）L， （Ci）L≤Ci≤（Ci）M（Ci）R-Ci（Ci）R-（Ci）M， （Ci）M≤Ci≤（Ci）R

利用隶属度函数将式（9）拆分为最好的规划和最差的规划：

minC1=∑ni=1（Ci）L+∑ni=1（Ci）M-∑ni=1（Ci）Lβ∑ni=1Xi（10）

s.t.

∑ni=1Xi≥Q

∑ni=1（Ci）L+∑ni=1（Ci）M-∑ni=1（Ci）Lβ≤CR-（CR-CM）β

Qai≤Xi≤Qbi

β∈[0，1]，i=1，2，3，…，n

minC2=∑ni=1（Ci）R-∑ni=1（Ci）R-∑ni=1（Ci）Mβ∑ni=1Xi （11）

s.t.

∑ni=1Xi≥Q

∑ni=1（Ci）R-∑ni=1（Ci）R-∑ni=1（Ci）Mβ≤CL+（CM-CL）β

Qai≤Xi≤Qbi

β∈[0，1]，i=1，2，3，…，n

这样，对问题的求解就转换为两个确定性线性规划问题的求解。

（四）确定分配目标

原油开采企业进行原油产量分配的目标通常包括利润最大化、产量最大化、成本最小化及其两两组合得到的多目标。原油开采企业应基于不同的市场环境背景选择不同的目标条件下的分配方案。原油开采企业在进行原油产量分配目标选择时应依据对原油价格的未来走势的判断来选择利润最大化、产量最大化或者成本最小化目标。

三、实例应用

本文基于某油田分公司11个采油厂进行实例分析。在计算成本时只考虑变动成本即操作成本，没有考虑固定成本，所以计算的利润均为非实际利润。

（一）基于模糊优化的某油田分公司原油产量分配方案

运用模糊优化方法在利润最大化、产量最大化或者成本最小化目标下制定方案，得到最优产量分配方案。

1.某油田分公司参数值、目标值预测

由于产量规划过程中存在不确定性，所以单靠一种预测方法得到的预测值作为参数值是不科学的，因此本文采用两种方法进行原油操作成本的预测。预测方法有很多种，常用的方法主要有经验法和模型法。模型法需要找出众多影响原油产量、成本消耗的因素，涉及面广，方法过于复杂。经验法是指根据已有的历史数据及其相应的规律运用数学方法建立数学模型并进行预测。基于数据收集的便捷性，本文采用简单可行的经验法。对操作成本的预测本文选择了经验法中的回归预测和适用于“小样本、贫信息”的灰色预测方法进行预测。对于原油价格的预测，本文没有进行详细预测，而是借鉴其他学者的油价预测结果作为本文原油价格的预测结果。

（1）操作成本测算

笔者通过实地调研得到某油田分公司2007—2013年单位操作成本，考虑到通货膨胀的影响，将历年的成本数据都折算到规划年，本文采用的折现率是3%，剔除了通货膨胀等对成本变化趋势的影响，具体数据因文章篇幅有限不一一列出。

1）回归预测

时间为自变量（2007年x=1，2014年x=8），单位操作成本为因变量，通过回归分析，获得产量与时间序列之间的关系，获得回归方程，应用该回归方程进行规划年操作成本的预测。以某油田分公司A采油厂为例具体说明预测过程。得到线性回归方程为：y=39171x+22858，相关系数为R2=09897。可见该回归方程显著，可用于预测规划年的操作成本，代入x=8，得到2014年A采油厂的单位操作成本点预测值为47032元/吨。

用同样的方法对其他采油厂进行操作成本的预测，结果如表2所示。

表2某油田分公司各采油厂规划年操作成本预测元/吨

采油厂回归方程R2预测值

Ay=39171x+228580989754195

By=29822x+298460949853703

Cy=34309x+298540940157301

Dy=44319x+244230853159878

Ey=21033x+316630860448489

Fy=82453x+491580795755754

Gy=2791x+360860931258414

Hy=6505x+430990704048303

Iy=53027x+370520955779474

Jy=8662x+361110671743041

Ky=15069x+267310798238786

2）灰色预测

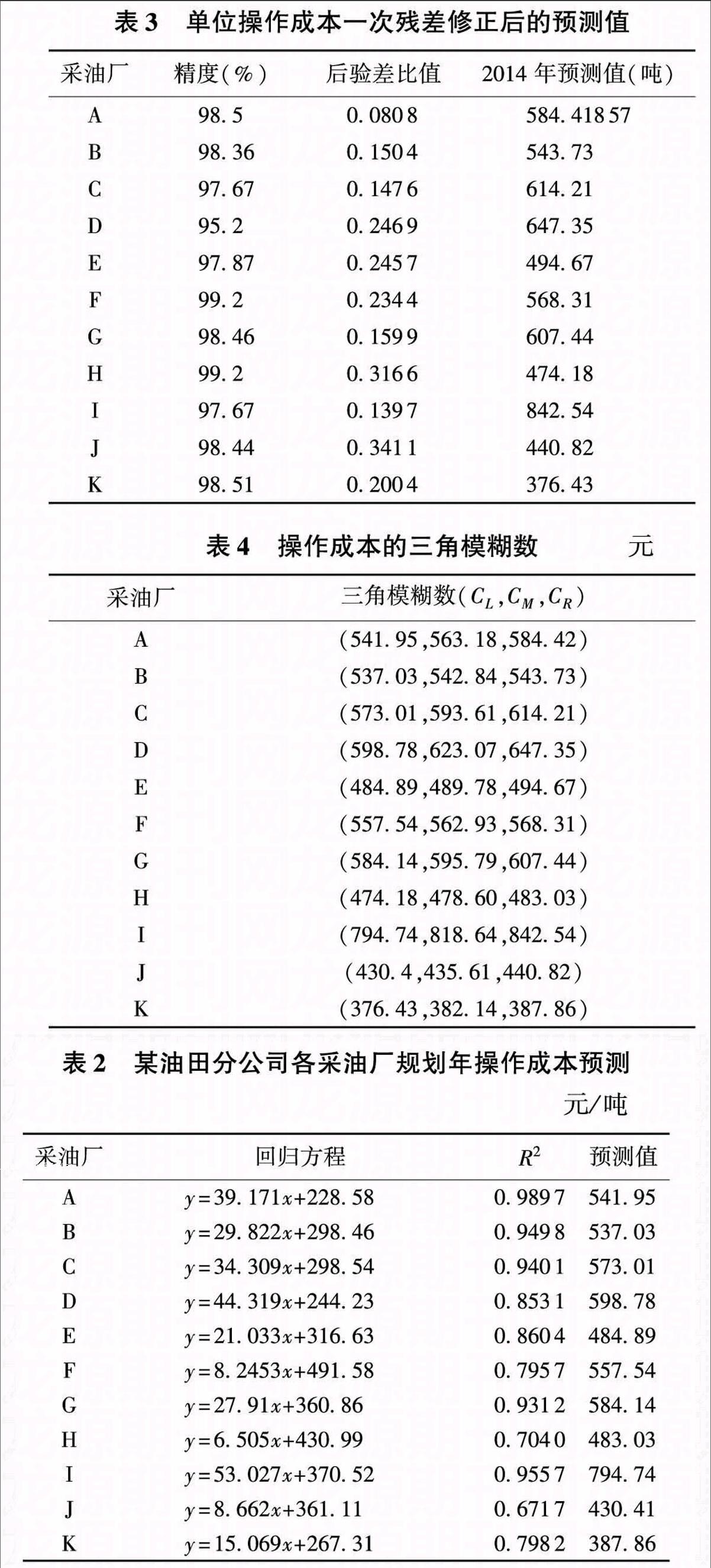
A采油厂2007—2013年单位操作成本为X（0）={28064，29055，34594，38433，42785，46478，50278}，不具备良好的灰指数律，应用累加生成建模法生成X（1）={28064，57119，91713，130146，172931，219409，269687}。将X（1）、X（0）分别代入累加矩阵B和常数项向量YN，得到灰参数a=-0102201，b=262997689，代入时间驱动函数x（t+1）=2853984148e0102201t-2573344148，递减还原累加生成数列，得到A采油厂2007—2013年拟合值。得到的灰色预测最大相对误差为570%，平均相对误差e（avg）为236%，精度为9764%，后验差比值为01234，小误差频率为1。为了进一步提高预测精度，采用残差序列继续建模，得到残差序列GM（1，1）模型为：x（t+1）=32093071e0232659t-15537836，一次残差修正后灰色预测最大相对误差为290%；平均相对误差e（avg）为149%，精度为9851%；后验差比值为00808，小误差频率为1。可见，一次残差修正后灰色预测效果很好，应用其进行2014年单位操作成本预测，得到预测值为58441857元/吨。

用同样方法，分别对其他几个采油厂进行灰色预测，可以得到其他10个采油厂的单位操作成本的一次残差修正后的预测值，见表3。

当后验差比值小于035，精度大于095时，表示拟合效果好，因此用灰色预测进行操作成本的预测拟合效果很好，预测值可以采用。

基于以上两种预测方法得到操作成本的上下限，上下限的平均值即为三角模糊数中的中间值，操作成本的三角模糊数见表4。

表3单位操作成本一次残差修正后的预测值

采油厂精度（%）后验差比值2014年预测值（吨）

A9850080858441857

B98360150454373

C97670147661421

D9520246964735

E97870245749467

F9920234456831

G98460159960744

H9920316647418

I97670139784254

J98440341144082

K98510200437643

表4操作成本的三角模糊数元

采油厂三角模糊数（CL，CM，CR）

A（54195，56318，58442）

B（53703，54284，54373）

C（57301，59361，61421）

D（59878，62307，64735）

E（48489，48978，49467）

F（55754，56293，56831）

G（58414，59579，60744）

H（47418，47860，48303）

I（79474，81864，84254）

J（4304，43561，44082）

K（37643，38214，38786）

上述所有计算均采用软件DPS v705计算。

（2）原油价格测算

对于原油价格的预测其他学者已进行了详细的研究，本文不对原油价格进行详细预测，主要是引用其他学者的研究成果。张跃军等回顾了2013年国际原油市场的发展动态，综合分析了2014年国际经济发展态势，综合考虑了原油市场的供需、美元汇率、投机操作等因素，预测2014年WTI和Brent原油现货价格将分别达到97～101美元/桶、111～117美元/桶。[10]范英等通过系统性分析了影响国际油价的主要因素，预测2014年WTI和Brent原油现货价格将分别达到95美元/桶、104美元/桶。[11]徐凌等运用差分自回归移动平均（ARIMA）模型对原油价格进行预测，得到2014年原油价格将在5025～7634美元/桶加上一定的“危机溢价”范围内波动。[12]李成等利用神经网络预测2014年原油价格为108美元/桶。[13]笔者利用上述的灰色预测中的GM（1，1）模型预测2014年原油价格为105美元/桶，具体预测方法和操作成本中灰色预测方法一致，数据统一采用WTI原油期货价格。本文运用不同预测方法得到的规划年原油价格预测值即原油价格的三角模糊数为（95，1015，108）美元/桶。将原油价格折算成人民币计量，即原油价格的三角模糊数为（4123，44051，46872）元/吨。

（3）原油开采税费率测算

原油开采企业涉及的税费主要有增值税、所得税、资源税、矿产资源补偿费、营业税、城建税、教育费附加、石油特别收益金和探矿权使用费等，所得税是针对利润征收的税费，对本文的产量分配优化结果不会产生影响，所以本文主要涉及的税费有增值税（销售收入的17%）、资源税（销售收入的38%）、矿产资源补偿费（销售收入的1%）、城建税（增值税的7%）、教育费附加（增值税的3%）、石油特别收益金（油价不同阶段征收比率不同，每桶油的特别收益金=（P-40）×征收比率-速算扣除率。以上税费的比例均为查阅相关文件获得，通过计算得每吨油的税费（235%×PQ+特别收益金）。结合上述对原油价格预测结果，规划年的原油开采吨油税费为：T=（635%×P-4557）元。

（4）模型目标值测算

中国石油天然气集团公司经济技术研究院编撰的《2013年国内外油气行业发展研究报告》预测，2014年中国石油需求量将达到518亿吨，即规划年预计石油需求量为518亿吨。历年中国石油需求量与某油田分公司的供应量的数据显示，某油田分公司需完成总需求量的044%，即规划年某油田分公司需满足的石油消费量约为228672万吨。某油田分公司的原油商品率为96%，为满足228672万吨的需求，某油田分公司需生产2382万吨的原油。预计规划年某油田分公司的总成本上限是350亿元，其历年固定成本与变动成本比例均在6∶4之间发生细微波动，所以规划年某油田分公司预计总变动成本在140亿元上下波动，本文估算的某油田分公司的总变动成本的三角模糊数为（139，140，141）亿元。

2.不同目标下某油田分公司分配模型求解

（1）利润最大化模型求解

将上述构建的利润最大化原油产量分配模糊优化模型，利用三角模糊数和隶属度函数转化为以下两个普通线性规划问题：

一是不同α、β水平下的最优解

maxπ1=PR-TR-∑11i=1（Ci）L-（PR-PM）α+（TR-TM）α+∑11i=1（Ci）L-∑11i=1（Ci）Mβ∑11i=1Xi （12）

s.t.

∑11i=1Xi≥Q

∑11i=1（Ci）L+∑11i=1（Ci）M-∑11i=1（Ci）Lβ≤CR-（CR-CM）β

Qai≤Xi≤Qbi

β∈[0，1]

i=1，2，3，…，11

二是不同α、β水平下的最劣解

maxπ2=PL-TL-∑11i=1（Ci）R-（PL-PM）α-（TL-TM）α-∑11i=1（Ci）R-∑11i=1（Ci）Mβ∑11i=1Xi （13）

s.t.

∑11i=1Xi≥Q

∑11i=1（Ci）R-∑11i=1（Ci）R-∑11i=1（Ci）Mβ≤CL+（CM-CL）β

Qai≤Xi≤Qbi

β∈[0，1]

i=1，2，3，…，11

将预测的结果代入式（12）和式（13），利用DPS v705软件对最优解方程和最劣解方程进行求解，并将最优解和最劣解的结果进行平均就可得到基于利润最大化目标的产量最优分配方案，具体如表5所示。

表5利润最大化的产量分配吨

采油厂分配产量采油厂分配产量

A4036300G1973600

B2573300H1658600

C2972600I995350

D284921213J1090100

E2619500K2154200

F2094000总产量2501676213

（2）产量最大化模型求解

当销售收入等于固定成本加变动成本再加上缴税费时，称这个点为原油开采企业的盈亏平衡点。盈亏平衡点的销售收入为

S=T+C （14）

式中

S=Q×α×P （15）

T=S×β （16）

C=F+V×Q （17）

将式（15）、（16）、（17）代入式（14）中得

Q×α×P=（S×γ）+（F+V×Q） （18）

式中，S为销售收入，单位为元；T为总税费，单位为元；C为总成本，单位为元；Q为总产量，单位为吨；

α为石油商品率，是百分数；P为原油销售价格，单位为元/吨；β为税费中与油价有关的总税率，是百分数；γ为税费中与产量有关的总税率，是百分数；F为与产量无关的年成本，单位为元；V是与产量有关的平均吨油成本，单位为元。式中与产量相关的成本主要是指操作成本。

当原油价格处于规划年预测区间时，S>T+C，即在规划年的预测油价范围内生产企业都是有利可图的，追求利润最大化和追求产量最大化的规划结果是一样的，即产得越多，利润就越大。所以本文对产量最大化不进行具体的计算，而是直接引用利润最大化分配的结果。

（3）成本最小化模型求解

将上述构建的成本最小化原油产量分配模糊优化模型，利用三角模糊数和隶属度函数转化为如下两个普通线性规划问题。

一是不同α、β水平下的最优解

minC1=∑11i=1（Ci）L+∑11i=1（Ci）M-∑11i=1（Ci）Lβ∑11i=1Xi （19）

s.t.

∑11i=1Xi≥Q

∑11i=1（Ci）L+∑11i=1（Ci）M-∑11i=1（Ci）Lβ≤CR-（CR-CM）β

Qai≤Xi≤Qbi

β∈[0，1]

i=1，2，3，…，11

二是不同α、β水平下的最劣解

minC2=∑11i=1（Ci）R-∑11i=1（Ci）R-∑11i=1（Ci）Mβ∑11i=1Xi （20）

s.t.

∑11i=1Xi≥Q

∑11i=1（Ci）R-∑11i=1（Ci）R-∑11i=1（Ci）Mβ≤CL+（CM-CL）β

Qai≤Xi≤Qbi

β∈[0，1]

i=1，2，3，…，11

同利润最大化的求解方法一样得到成本最小化目标的产量分配方案，具体如表6所示。

表6成本最小化的产量分配吨

采油厂分配产量采油厂分配产量

A4025850G1636200

B2573300H1658600

C2788200I978200

D2212300J1090100

E2619500K2154200

F2083550总产量23820000

（二）小结

从某油田分公司模糊优化的原油产量分配方案的实例应用，得到其规划年基于三大目标下的产量分配方案。利润最大化时的规划方案如表5所示，总利润为347.447亿元～404.709亿元；成本最小化时分配方案如表6所示，总利润为352.00亿元～399.17亿元。有效的原油产量分配方案有利于降低企业成本、提高企业利润，同时有助于企业经营运行的顺利进行，为某油田分公司进行生产规划提供重要的理论依据和现实指导。

四、结语

原油产量分配是一个庞大的系统工程，涉及公司战略、企业运营等各个方面，因此，在进行原油产量分配时必须树立科学发展观，要统筹规划，从整个公司层面上来分析问题，制定科学合理的规划方案。建议原油开采企业在合理性、实用性和可操作性原则下，根据原油产量分配过程中系数、预测方法和约束条件的不确定性，构建利润最大化、产量最大化和成本最小化三大目标下的产量分配模糊优化模型，并利用三角模糊数和隶属度函数将构建的模糊优化模型转换成确定性优化模型，通过求解得到模糊条件的最优产量分配方案。

企业应在不同条件及要求下选择不同的方案。当利润最大化为考核指标时，基于利润最大化求解的产量分配方案即为利润最大化目标下的最优分配方案。当成本最小化为考核指标时，基于成本最小化求解的产量分配方案即为最优分配方案。当预测原油价格未来几年呈上涨趋势时，原油开采企业一般希望在原油价格更高时再将原油开采出来或者将开采的原油储藏起来等待价格更高时再将原油销售出去，从而使原油开采企业的总效益达到最大，所以，此种情况下原油开采企业应该选择在满足国内基本需求的前提下实现成本最小化的方案。相反，当预测原油价格未来几年呈下降趋势时，开采企业希望尽量多开采原油并尽快销售出去，以使原油开采企业总效益达到最大，所以，此种情况下原油开采企业应该选择在产能约束和投资约束的制约下实现利润最大化、产量最大化的分配方案。

[参考文献]

[1] Aronofsky. Alinear Programming Model for Scheduling Crude Oil Production[J].Journal of Petroleum Technology，1958（8）：1519.

[2] 杜军.原油价格波动对国内石化企业的影响及对策分析[D].南京：东南大学经济管理学院，2003.

[3] 刘志斌，丁辉，等.油田开发规划产量构成优化模型及其应用[J].石油学报，2004，25（1）：6265.

[4] 姜少慧. 胜利油田产量成本分配方法研究[D].东营：中国石油大学（华东）经济管理学院，2007.

[5] 李博然. 基于免疫微粒群算法的油气配产问题研究[D].东营：中国石油大学（华东）经济管理学院，2011.

[6] Buckley J J. Possibilistic Linear Programming with Triangular Fuzzy Parameters[J]. Fuzzy setsand system， 1988， 26：135138.

[7] H Zimmermann. Fuzzyprogramming Andlinear Programming with Seceral Objectivefunctions[J]. Fuzzy Sets and Systems， 1978，1：4651.

[8] 盖英杰，李树荣.油田开发规划优化理论与实践[M].东营：石油大学出版社，2002.

[9] 李孝忠，张庆德.具有模糊变量和模糊约束的模糊线性规划问题[J].聊城师范学院学报：自然科学版，1998，11（1）：711.

[10] 张跃军，达亚彬，张璐，等. 2014年国际原油市场分析与价格预测[J]. 北京理工大学学报：社会科学版，2014，（2）：1317.

[11] 范英，姬强. 2013年国际原油市场走势分析与价格预测[J]. 中国科学院院刊，2013（1）：7984.

[12] 徐凌，黎佳卉，李亮. ARIMA模型在国际原油价格预测中的应用[J]. 河南科学，2013（5）：692695.

[13] 李成，周恒. 原油价格改进型神经网络预测方法[J]. 统计与决策，2013（8）：6769.

[责任编辑：陈可阔]