北方某滨海核电温排水分布规律计算分析
付斌 吴修锋
DOI:10.16661/j.cnki.1672-3791.2015.36.044
摘 要:感潮河段水流受上游径流和外海潮汐的双重影响,电厂温排水模拟具有较大的难度。一般而言,河口地区受潮汐影响较大,径流作用相对较弱。该文采用平面二维水流温升场数学模型对位于河口地区的北方某核电厂温排水进行了计算分析。在验证计算的基础上,对不同季节、不同机组容量下的温排水分布规律进行了预测分析,为核电厂取、排水工程布置及环境影响评价提供了依据。
关键词:潮汐 径流 温排水 数学模型
中图分类号:TM623 文献标识码:A 文章编号:1672-3791(2015)12(c)-0044-04
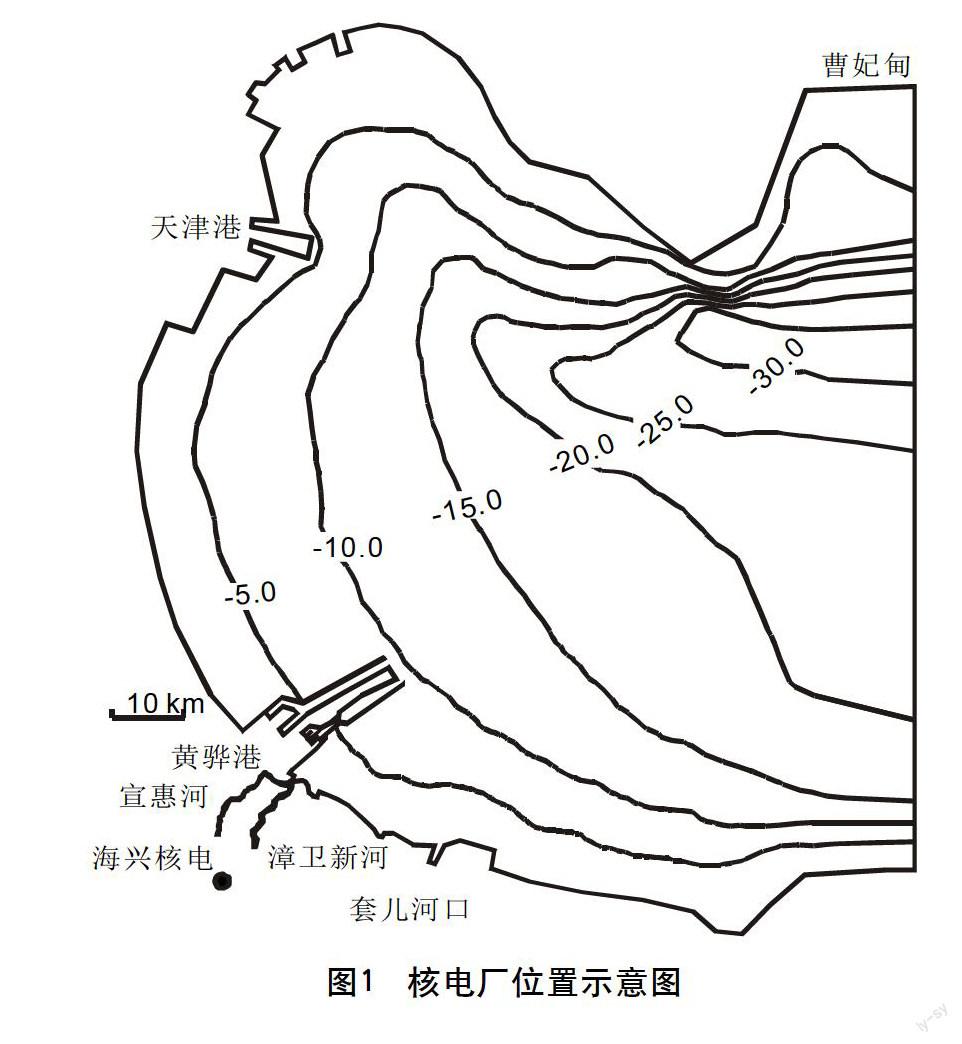
以位于我国渤海湾近岸海域的某核电厂为例(见图1),选用沿水深平均的二维水流温升场数学模型进行潮流场和温升场的计算,研究潮汐与径流共同作用下电厂温排水的分布规律,为电厂取排水工程布置及环境影响评价提供依据。
核电厂位于河北省海兴县,电厂通过管道从黄骅港港区取水,取水管线长约28 km;通过长约10 km的沟渠将温排水排入宣惠河,再通过该河道进入渤海湾。
核电厂规划容量6台机组,夏季最大排水流量为5.08 m3/s,排水温升5.63 ℃;冬季最大排水流量为3.27 m3/s,排水温升9.70 ℃。
1 数学模型
针对电厂所在海湾的形状及潮流特征,选用沿水深平均的平面二维潮流温度场数学模型。在计算时,河道给以流量边界,外海给以潮位过程条件。
该数学模型控制方程属混合型算子方程,可采用剖开算子法求解。由于避开了人工滤波方法,该方法具有良好的计算稳定性和较高的计算精度[1-3]。
2 计算条件
2.1 水文条件
利用原型观测水文资料(2014年6月14日~2014年6月15日大潮过程)作为水流数学模型验证的水文条件。
根据黄骅港潮位站的潮位统计资料,典型潮型分别选取典型半月潮水文条件。
2.2 计算参数
根据计算海域的实际情况,海床糙率选取0.016~0.020;水面综合散热系数按照《工业循环水冷却设计规范》推荐的公式确定,为安全起见,在计算该参数时不考虑风速的影响;扩散系数选用Ex=10.0 m2/s,Ey=5.0 m2/s。
在实际计算时,上述参数根据模型验证计算结果可进行适当调整。
3 模型验证
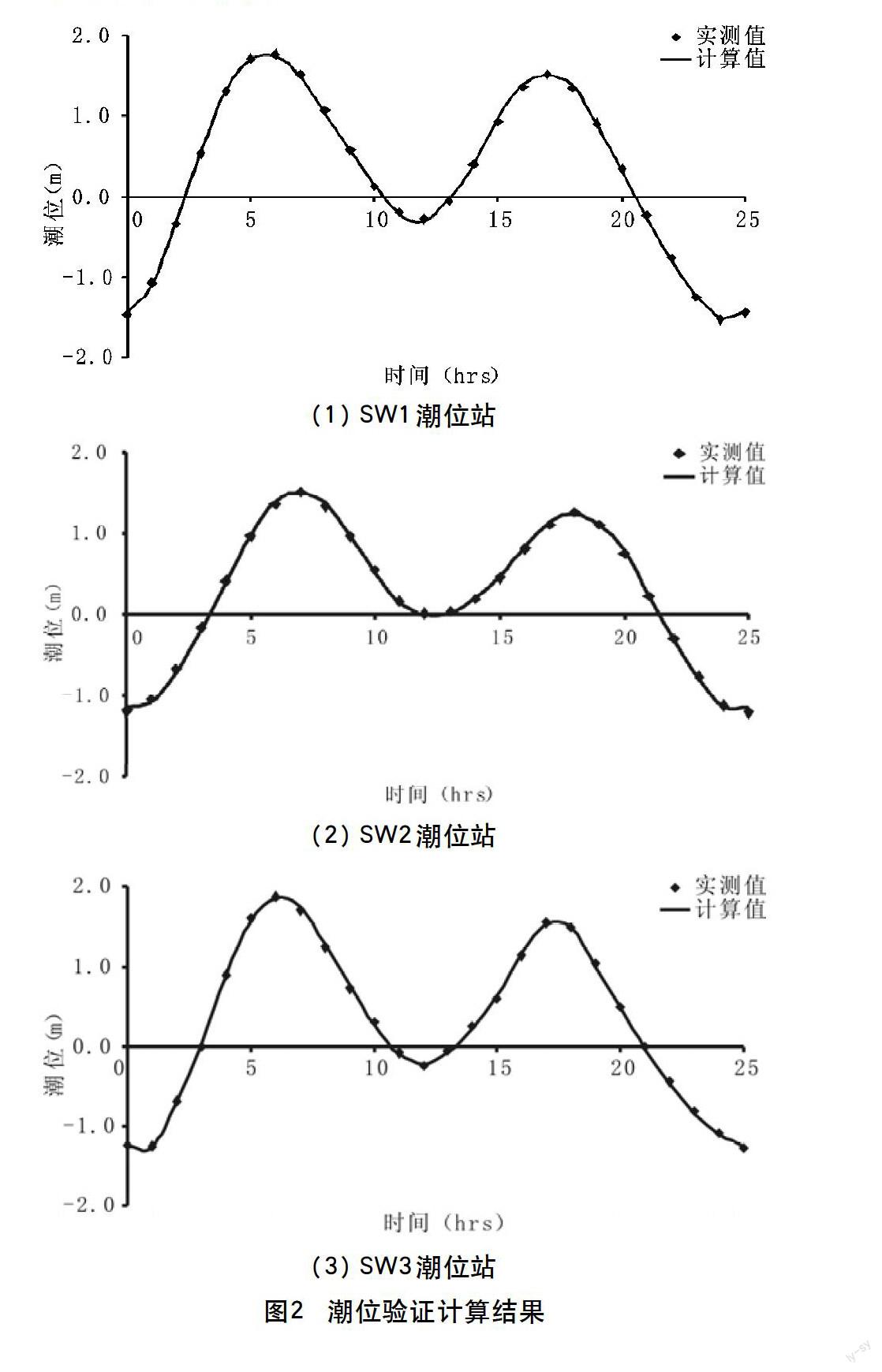
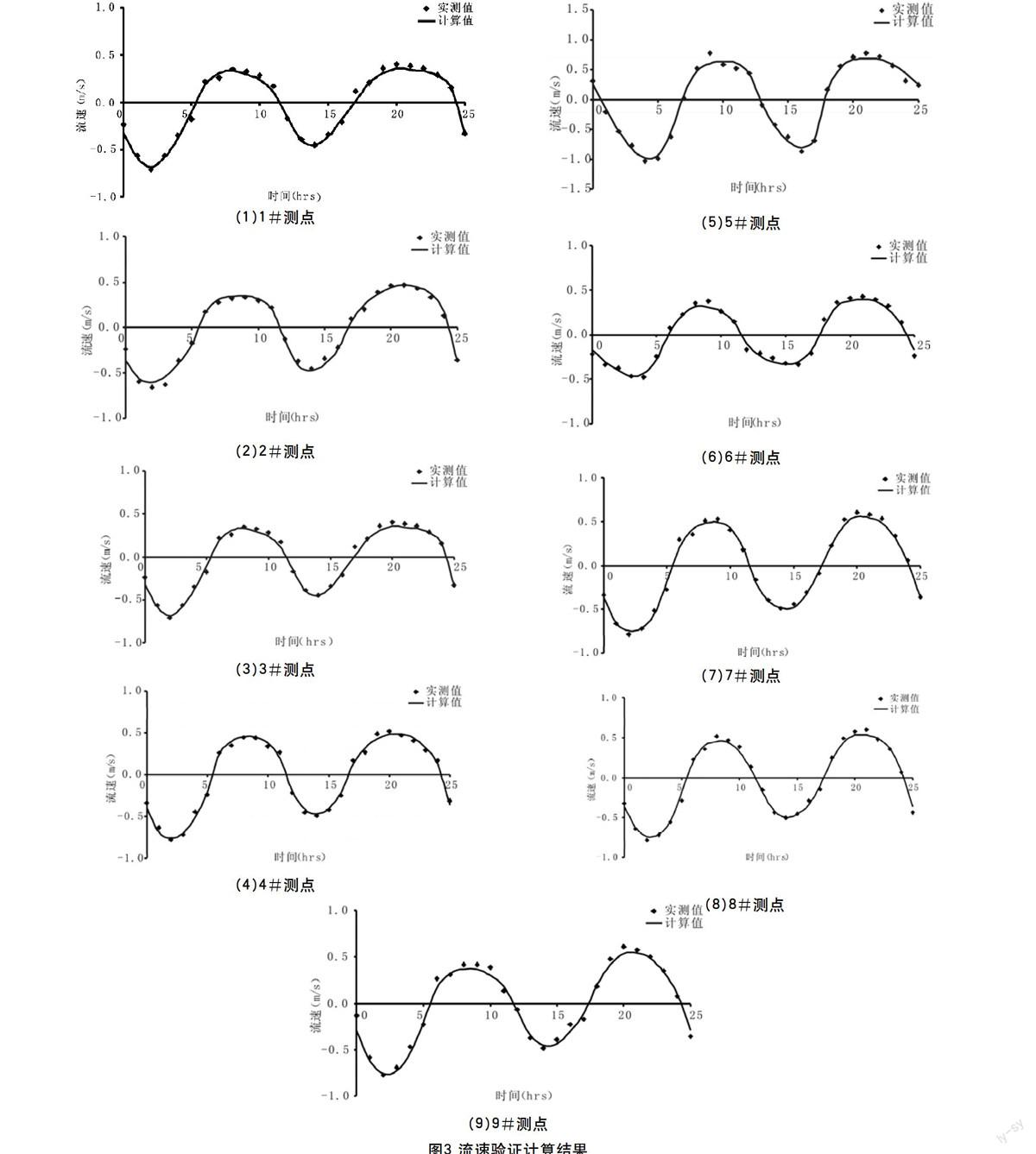
结合原型水文观测资料,对上述建立的平面二维水流数学模型进行了验证计算。图2、3分别为实测大潮水文条件下的潮位和流速验证计算结果。在流速验证中,不失一般性,以涨潮流为正、落潮流为负。由图可见,在实测水文条件下,3个临时潮位站的潮位计算值与实测值吻合较好,9条测速垂线的垂向平均速度变化过程的计算值与实测值也较为一致,表明建立的平面二维水流数学模型较好地模拟了电厂附近海域的水流变化情况,其计算结果是可信的,选取的计算参数是合理的。
图4为计算海域典型时刻潮流场。由图可见,计算海域涨落潮流变化较为明显;此外,由于浅滩较多,在低潮位时常有边滩露出,滩槽流速差异较为明显。由于在计算中采用了动边界处理技术,随潮位变化而产生的滩体出露现象得到了较好地体现。
4 温排水成果分析
图5为核电厂不同季节、不同机组容量时的全潮最大温升包络线,由图5可见。
(1)核电厂在宣惠河上游河道排水,虽然机组排水量很小,不过由于宣惠河上游受闸坝控制,基本没有来流,只能依靠外海涨、落潮流对温排水进行掺混、稀释,计算水文条件下电厂温排水在涨潮时段被涨潮流带向排水口上游河道,在落潮时段被落潮流带向排水口下游河道。
(2)电厂厂址到宣惠河河道之间的陆域明渠长约10 km,考虑该部分水面对温排水的温降作用后,核电温排水对宣惠河的影响程度有所降低,且温升越高,降低程度越明显。不同季节、不同运行工况平均来看,4.0 ℃温升面积降低了约50 %,3.0 ℃温升面积降低了约58 %,2.0 ℃温升面积降低了约70 %,1.0 ℃温升面积降低了约75 %,0.5 ℃温升面积降低了约84%。
(3)考虑陆域明渠的温降作用后,核电在宣惠河河道内的温升影响长度有所降低:以1.0 ℃全潮最大包络线为例,其最远扩散直线距离约为10.0 km,距河口直线距离约1.8 km;最远扩散河道距离11.5 km,距河口河道距离约3.7 km。
(4)核电温排水主要集中在宣惠河河道内,0.5 ℃温升最大影响范围尚未到达河口区,对外部渤海海域及河口外湿地保护区的温升影响小于0.5 ℃。
5 结语
感潮河段水流受上游径流和外海潮汐的双重影响,电厂温排水模拟具有较大的难度。一般而言,河口地区受潮汐影响较大,径流作用相对较弱。该文所研究的核电厂所处河道上游有闸门控制,基本无下泄水流,下游在河口处断面缩窄,并与漳卫新河交汇,因此温排水受既受外海潮汐影响,也受其他河道径流影响,温排水分布规律有一定的特殊性。
参考文献
[1] Daoyang Ding, Philip L-F Liu.An operator-splitting algorithm for two-dimensional convection dispersion reaction problems[J].Int.Methods Eng,1989,28(5):1101-1108.
[2] 吴时强,丁道扬.剖开算子法解具有自由表面的平面紊流速度场[J].水利水运工程学报,1992(1):39-48.
[3] 时强,丁道扬,吴碧君,等,平面二维动态水质数学模型[J].水动力学研究与进展,1996(6):653-660.

