LNG输送管道耦合传热的数值模拟

胡卓焕，黄天科，张乐毅，杨茉

（上海理工大学能源与动力工程学院，上海200093）

引 言

天然气作为一种高效而清洁的能源，近年来在世界能源市场结构中的比例不断增加，得到了越来越广泛的应用［1］。我国也非常重视LNG的应用和LNG加气站的建设，随着LNG汽车的推广，我国LNG气站数量迅速增长，由最初2007年仅在北京、上海、乌鲁木齐等地的6个气站发展到2014年总数接近2500个。LNG的密度是天然气的600倍，而重量仅为同体积水的45%左右。天然气液化输送相对于气态输送来说具有很多显著的优点，输送相同质量的天然气，LNG输送管的直径要小得多，通过管道输送液化天然气 （LNG）具有显著的经济优势和发展潜力［2］。

低温LNG的输送管道可分为3类：非绝热管道、普通绝热管道以及真空绝热管道［3］。非绝热管道通常用于间断性的短距离输送，虽然造价低，但在使用时冷量 损失较大；真空绝热管道虽然冷量损失少，但造价和施工管理费用高。对于大批量LNG的长距离输送，通常采用普通绝热管道。这种管道是在LNG管道外敷设一定厚度的隔热材料，其绝热性能比真空绝热管道差，但其投资和施工管理费用比真空绝热管小，综合各方面因素考虑，普通绝热管道较适合长距离输送。

许兴华等［4］运用理论分析与经验公式相结合，采用Matlab科学计算软件对某液化天然气加气站管道进行热力分析，提出了一种计算液化天然气加气站管道冷量损失的方法。但是计算中未考虑周围空气流动和环境温度等的变化导致的保温层外表面对流换热系数的变化以及太阳能辐射等因素对管道热力性能的影响。谢刚等［5］对LNG管路保温厚度进行了理论分析计算，分析了保温层经济厚度计算方法、防止表面凝露的保温层厚度计算方法和控制最大允许冷量损失的保温层厚度计算方法，并用实例进行了验证。包臣等［6］对保温层中温度场进行了数值模拟，但是对空气对流换热系数采取了取定值的方法，未能分析保温层外表面的对流换热系数受外界影响变化的情况。

本研究结合工程实际工况建立LNG管道二维稳态传热模型。由于LNG的输送是在－150℃以下的低温环境下进行［7－8］，LNG与管道外部环境温度之间有较大的温差，从而使得LNG在管道输送过程中与外界环境进行热量交换，造成大量的冷单量和冷量 损失。在这个复杂的传热过程中，由保温特性，太阳辐射等因素都会产生重要的影响。因此，对LNG管道在与外界环境之间进行耦合传热分析就显得尤为重要［9－10］，对于计算LNG输送过程中的冷量 损失、设计合理保温层厚度以及对LNG管道建设的经济性评估具有一定的实际意义。

同时，耦合传热问题也引起了很多研究者的关注［11－15］。为此，本研究以某天然气管道为例，通过对LNG管道进行耦合传热分析比较了不同环境温度、保温层厚度、Reynolds数和辐射强度对管道冷量和冷量 损失的影响，进一步分析了在现实工况下LNG管道的冷量 损失计算方法，为LNG管道实际的工程设计、运行优化和节能技改等提供科学依据。

1 理论分析

LNG输送管道在实际使用中，采用埋地敷设时，保温层受压后将导致传热系数增加，保温效果降低，同时不便于施工和检查维护，因此常采用架空敷设的方式［16］。由于输送LNG管道的长度相对管径来说较长，在输送过程中流过单位长度LNG管道温度的变化可以忽略不计，故可不考虑LNG沿管道长度方向的热量传递，管道内的LNG冷量损失主要来自LNG与保温层之间的导热以及保温层外表面与周围环境之间的对流和辐射的热交换。根据LNG管道保温材料厚度的不同，这3种热量传递形式都对LNG的冷量损失产生一定的影响。LNG管道耦合传热如图1所示。

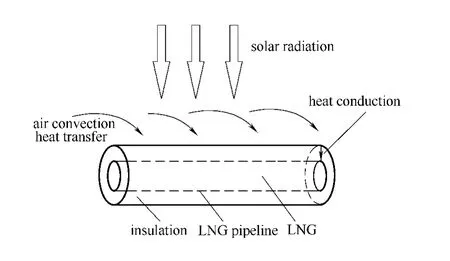
图1 LNG管道耦合传热示意图Fig.1 Coupled heat transfer for pipeline

1.1 导热

导热是在固体内部热量从温度较高部分传递到温度较低部分的现象。在LNG管道中热量在管壁和保温层内的传递就是导热。LNG管道可视为圆柱体，单位长度LNG管道与外界环境之间的导热热阻计算公式为［17］：

式中，R为热阻，单位为 m·K·W－1；λ1、λ2分别为LNG管道和保温材料的热导率，单位为W·m－1·K－1；d1、d2、d3分别为LNG管道内径、管道外径和保温层外径，单位为m。

单位长度LNG管道与外界环境之间的导热热流量：

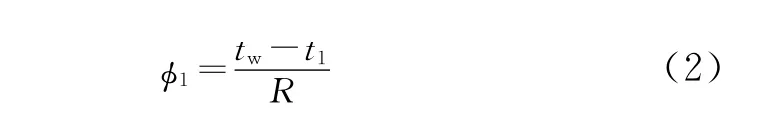
式中，φ1为通过保温层导热热流量，单位为W；tw为壁面温度，t1为LNG管道内表面温度，单位均为K。

1.2 对流

流体流过一个物体表面时与物体表面间的热量传递过程称为对流换热。对流换热分为强制对流换热与自然对流换热两类。LNG在管道内运输时与管壁的换热是强制对流换热，管外保温层与环境的换热是自然对流换热，其热流量：

式中，φ2为保温层外表面对流换热热流量，单位为W；h为对流换热传热系数，单位为W·m－2·K－1；A为辐射面积，单位为 m2；tw为壁面温度，tf为周围环境温度，单位均为K。

对流换热是一个复杂的质能交换过程，对流换热传热系数与固体表面粗糙度、几何形状、所处的环境温度和空气的传导率等因素有关。LNG管道截面保温如图2所示。

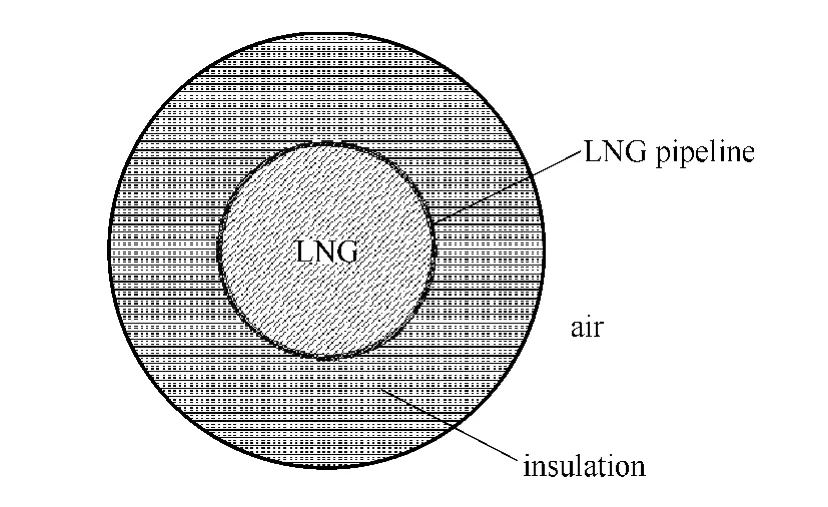
图2 LNG管道截面保温示意图Fig.2 Cross section of LNG pipeline

由于管道内低温的LNG以一定的速度流动，管道内壁与LNG之间为强制对流换热，其对流换热传热系数可按照以下公式确定［17］：

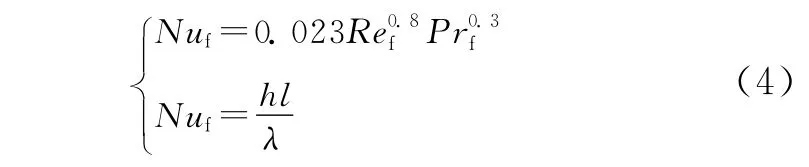
式中，Nuf为Nusselt数，Re为Reynolds数，Pr为Prandtl数，l为管道长度，h即为对流换热传热系数。

保温层外壁与周围空气之间为自然对流换热，自然对流是由于空气热胀冷缩产生的浮升力所造成［18］。根据对流微分方程组，可以得出自然对流换热的准则方程式：

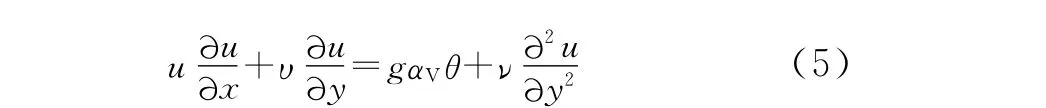
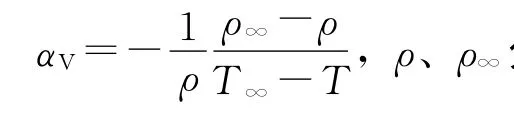
1.3 辐射

物体因热而发出电磁波来传递能量的方式称为热辐射。任何有温度的物体都在不断地向空间发出热辐射，同时吸收其他物体的辐射。LNG管道保温层外表面受周围环境及太阳辐射的影响，所以在进行LNG管道热力分析时辐射也应考虑在内。物体处某一环境下的辐射热量应由斯忒藩－玻耳兹曼定律计算［10］：

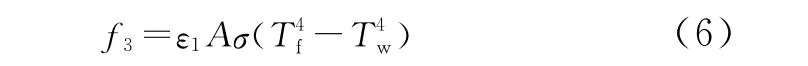
式中，ε1为物体的发射率；σ为斯忒藩－玻耳兹曼常数，又称黑体辐射常数，单位为W·m－2·K－4；A为辐射面积，单位为m2；Tf为物体温度，Tw为外界环境温度，单位均为K。

任何外界辐射量都可视为某一环境温度下某一物体的热辐射。本研究将不同的外界辐射量换算为不同的环境温度下LNG管道的辐射散热来进行计算。

1.4 耦合传热

LNG管道的耦合传热模型如图1所示。LNG与周围之间的传热包括导热、对流和辐射［19］，分别为上述式 （2）、式 （3）和式 （6）。根据以上各式的定义，可得：

即LNG在其输送管道中的冷量损失为保温层外表面对流换热量和辐射换热量之和。

2 模型建立

2.1 问题描述

以某LNG气站为例。LNG管道内径179 mm，外径188mm，材质为0Cr18Ni9，热导率为λ＝11.8W · m－1· K－1。 保 温 材 料 为 LT／Armaflex系列保温材料，热导率为λ＝0.015W·m－1·K－1。LNG泵提供1.194MPa压力，温度为－158℃。管道全线平均压力p＝1MPa，管道终压p＝0.856MPa，温度为－154℃。LNG密度ρ＝415.205kg·m－3，比定压热容cp＝3487.9J·kg－1·K－1，运动黏度ν＝1.54×10－7m2·s－1。LNG保温层厚度为145mm，管道终点LNG温度为－154℃，LNG全程处于液态。

选取LNG管道、保温材料以及周围环境为研究对象，该过程为三维传热过程。而在实际过程中，由于管道较长，LNG在输送过程中单位长度内温度变化较小，故本研究忽略保温层及LNG的轴向传热，整个传热过程可以简化为由外界通过保温层和管道向LNG传热的一个二维传热问题。LNG与管道内壁之间可简化为第三类传热边界条件，其对流换热传热系数可根据式 （2）确定。保温层外界的空气采用Boussinesq假设，通过建立数学模型，其模拟区域如图3所示。

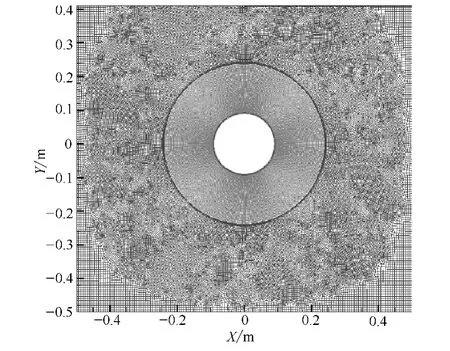
图3 LNG管道传热物理模型及网格划分Fig.3 Physical model and grids partition

根据边界层理论，靠近保温层外表面部分由于对流引起的流动以及温度的变化相对比较剧烈。为保证数值模拟的精度，在划分计算模型网格时，靠近保温层外表面部分的网格划分相对比较密，而其他部分的网格划分相对比较稀疏。

2.2 模拟结果及分析

本研究以上述物理模型为例，从不同保温层特性、Reynolds数、环境温度以及辐射强度等方面研究其对传热过程的影响。

在2.1节问题描述中的工况，在不考虑太阳辐射及空气强制对流对传热的影响时，在保温层外表面与周围环境自然对流的条件下，环境温度为293.15K时，得到LNG管道外表面平均温度为291.76K，LNG流经每米管道的冷量损失为17.62W·m－1，冷量 损失为26.53W·m－1。

管道保温层内及周围空气的温度分布如图4所示。图中等温线分布基本为同心圆环，由此说明了在整个传热过程中热阻主要集中在保温层内部，外界的空气自然对流对其传热影响较小。

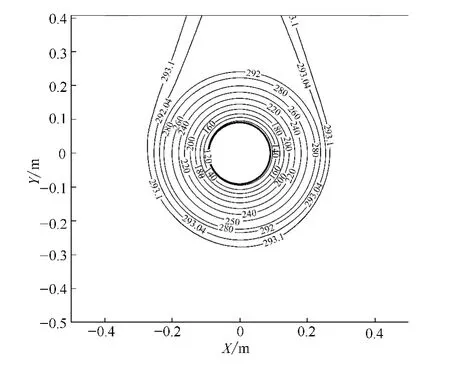
图4 自然对流状况下保温层及周围温度分布图Fig.4 Temperature distribution around pipeline on condition of natural convection

2.2.1 不同环境温度的影响 分别取环境温度273.15、283.15、293.15、303.15、313.15K，进而研究外界环境温度变化对LNG热力性能的影响。通过仿真模拟得到结果，具体如图4所示。随着环境温度的增加，LNG管道的冷量和冷量 损失均有明显的增加。这是因为，随着内外温差的增大，保温层中温度梯度增大，造成了LNG冷量和冷量 损失的增加。

由图5可见，当温度升高到40℃时，冷量损失较10℃时约增加20%左右。环境温度每升高10℃，LNG管道的冷量损失增加1.02W·m－1左右，冷量 损失约增加3.04W·m－1。

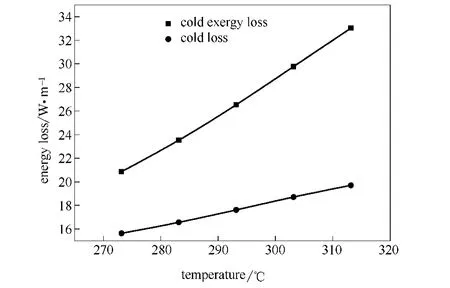
图5 不同环境温度对管道热力性能的影响Fig.5 Effect of environment temperature on energy loss

2.2.2 不同Reynolds数的影响 在无风情况下，LNG管道保温层外表面通过自然对流的形式与外界换热。空气流动使得保温层外表面与空气对流换热得到强化，传热系数增加，造成管道冷量和冷量增加。通过Fluent数值模拟得到，随着风速的变化，当Reynolds数从1.5×104到3×105时（即风速为0.5m·s－1到10m·s－1范围）时，LNG的冷量和冷量 损失如图6所示。随着Reynolds数的增加，保温层表面的对流换热传热系数增大，但冷量损失增加不明显。由此可得，LNG管道与外界热交换的热阻主要集中在保温材料层，减小保温层表面与空气的对流换热对于改善LNG管道的绝热性能作用不明显。

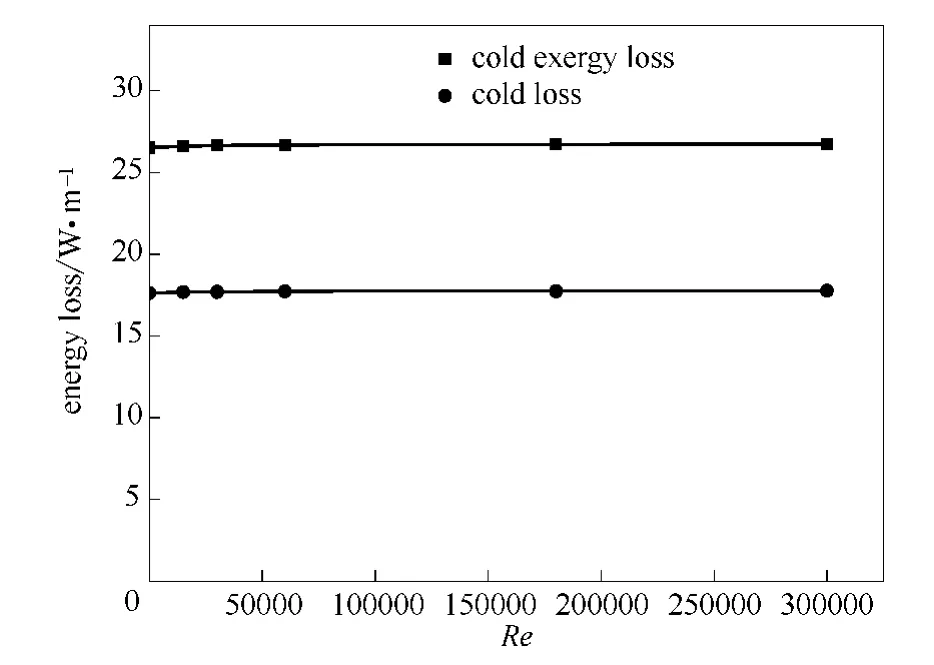
图6 不同Reynolds数对管道热力性能的影响Fig.6 Effect of Reynolds number on energy loss

2.2.3 不同太阳能辐射的影响 以夏季中午太阳能辐射为1350W·m－2为例，分别取最大太阳能辐射以及最大辐射的75%、50%和25%，分析太阳能辐射对2.1节中所取模型的LNG管道热力性能的影响 （假设保温层表面发射率为0.8），如图7所示。随着太阳能辐射的增加，保温层表面平均温度升高，LNG冷量损失和冷量 也逐步增加。

若保温层外表面不加遮热板或防辐射涂层，当辐射强度为1350W·m－2时，与无太阳光辐射时相比，冷量损失增大25%左右。但在实际工程中保温层表面采用单层、多层遮热板或防辐射涂层，这对于降低由辐射造成的LNG冷量损失有重要意义。

2.2.4 不同保温材料厚度耦合传热的影响 以上讨论了不同的环境温度、保温层表面换热传热系数以及太阳能辐射对LNG管道传热的影响。文献［7］给出了达到一定绝热性能所需保温层厚度的计算方法及其计算公式。在实际工程应用中，往往是通过设计不同厚度的保温材料达到一定的绝热性能要求［16］，上述各种因素对绝热性能的影响均对最终保温层厚度的设计产生影响。

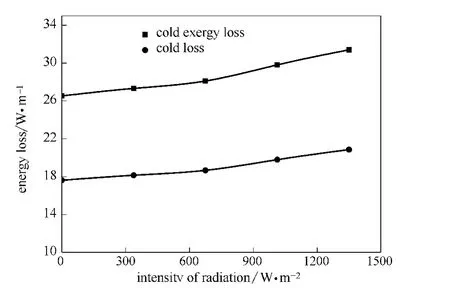
图7 不同太阳辐射强度对管道热力性能的影响Fig.7 Effect of intensity of radiation on energy loss

由此，本研究计算了环境温度分别为273.15、283.15、293.15、303.15和313.15K时，保温层厚度分别为72.5、108.75、145、181.25和217.5 mm情况下LNG管道冷量损失和冷量 的变化情况，如图8和图9所示。

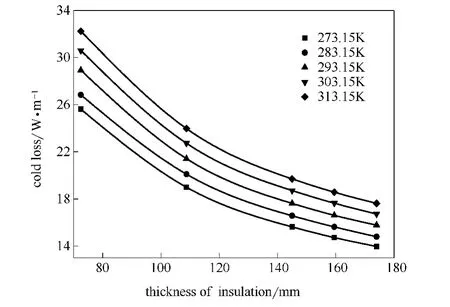
图8 保温层厚度与冷量损失图Fig.8 Effect of thickness of insulation on energy loss under different temperature

由图8和图9可知，对于一定的环境温度，保温层厚度较薄时，增加保温层厚度对于降低LNG管道冷量损失有明显的作用。随着保温层厚度的增加，管道冷量损失减小，继续增加保温层对改善其绝热性能作用有限。保温层厚度增加，使得LNG管道建设投资增加，经济性下降。当保温层厚度较薄时，环境温度的变化对保温层冷量和冷量 损失的变化产生明显的影响，随着保温层厚度的增加，外界环境的变化对管道冷量损失的影响逐渐减小。

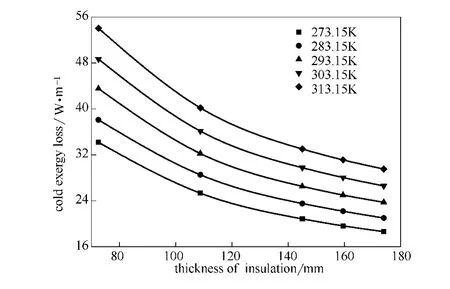
图9 保温层厚度与冷量 损失关系图Fig.9 Effect of thickness of insulation on cold exergy loss under different temperature

3 结 论

对LNG管道与周围环境之间的导热、对流和辐射的耦合传热进行了数值分析，通过比较不同的环境温度、Reynolds数和辐射强度以及保温层特性得出以下结论。

（1）外界环境的温度对LNG管道的冷量损失影响显著，环境温度每升高10℃，LNG管道的冷量损失约增加1.02W·m－1。对LNG保温材料厚度进行设计和计算时，应充分考虑当地最高气温对管道冷量损失的影响。

（2）LNG管道周围的强制空气流动会对保温层表面对流换热传热系数产生一定影响。但是与保温材料热阻相比保温层表面对流换热热阻相对较小，保温层表面换热传热系数的改变对LNG管道的冷量损失影响不大。

（3）阳光辐射对LNG管道的冷量损失影响较大，在LNG管道保温层表面加遮热板或防辐射涂层对改善绝热性能有重要意义。

（4）通过不同的保温材料的厚度对LNG冷量损失的影响可以发现，保温材料的厚度对LNG管道的冷量 损失影响较大。当保温材料的厚度较薄时，LNG管道的冷量和冷量 损失受外界温度变化的影响较大，随着保温层厚度的增加，外界环境的变化对管道冷量 损失的影响逐渐减小。

［1］ Tang Jianfeng （唐建峰），Cai Na （蔡娜），Guo Qing （郭清）.Simulation of LNG diffusion：a continuous vertical jet release ［J］.CIESCJournal（化工学报），2013，64 （3）：1124－1131.

［2］ Lu Chao（卢超），Zhuan Rui（耑锐），Yi Chongchong （易冲冲），Wang Wen （王文），LüJun （吕俊），Wang Lei（王 蕾 ）.BOG pre－cooling numerical simulation at LNG transport pipeline ［J］.Cryogenics（低温工程），2012，（6）：51－56.

［3］ Liang Guangchuan （梁光川），Zheng Yunping （郑云萍），Li Youlü （李又绿），Gao Aihua （高 爱 华），Pu Hongbin（蒲宏斌）.Long distance pipeline transportation technology in LNG ［J］.NaturalGasandOil（天然气与石油），2003，21（2）：8－10.

［4］ Xu Xinghua（许兴华），Wang Lu （王璐），Zhan Fushuai（战 福 帅 ），Liu Xirong （刘 锡 荣 ）.Thermal analysis on pipeline of liquefied natural gas automobile filling stations［J］.Petro－ChemicalEquipment（石 油 化 工 设 备），2014，43 （5）：49－53.

［5］ Xie Gang （谢 刚 ），Wang Tianming （王 天 明 ），Shao Yongjun（邵拥军），Wang Chunyan（王春燕）.Calculations for the heat insulation thickness of LNG Pipe ［J］.Chemical EngineeringofOil＆Gas（石油与天然气化工），2007，36（5）：373－375.

［6］ Bao Chen （包 臣），Mo Haiyuan （莫 海 元）.Numerical simulation on temperature field of cold－keeping layer of LNG pipelines ［J］.ContemporaryChemicalIndustry（当 代 化工），2013，42 （11）：1608－1610.

［7］ Li Yajun （李亚军），Chen Meng （陈蒙）.Simulation－based optimization and analysis of BOG multi－stage compression and recondensation process at LNG receiving terminal ［J］.CIESCJournal（化工学报），2013，64 （3）：986－992.

［8］ Wang Tao （王 弢 ），Lin Wensheng （林 文 胜 ），Gu Anzhong （顾安忠）.Analysis of working fluid and variable working conditions of organic Rankine cycle utilizing LNG cold energy ［J］.CIESCJournal（化 工 学 报），2010，61（S2）：107－111.

［9］ Zhang Hongwei（张宏伟），Tao Wenquan （陶文铨），He Yaling（何 雅 玲），Feng Zhenping （丰 镇 平）.Numerical study on coupled heat transfer of thrust chamber with regenerative cooling ［J］.JournalofAerospacePower（航空动力学报），2006，21 （5）：930－936.

［10］ Li Longjian（李隆键），Liu Hongtao（刘洪涛），Cui Wenzhi（崔文智）.Conjugated heat transfer of natural convection in pool with internal heat sources and convection in the tube［J］.NuclearPowerEngineering（核动力工程），2007，28（3）：32－37.

［11］ Jurgen G，Stefan G.Coupling methods for heat transfer and heat flow：operator splitting and the parareal algorithm ［J］.JournalofMathematicalAnalysisandApplications，2012，388：873－887.

［12］ Sun H，Li H，Yang D.Coupling heat and mass transfer for agas mixture－heavy oil system at high pressures and elevated temperatures ［J］.InternationalJournalofHeat＆MassTransfer，2014，74 （5）：173－184.

［13］ Zhang L，Liu X，Jiang Y.Exergy analysis of parameter unmatched characteristic in coupled heat and mass transfer between humid air and water ［J］.InternationalJournalof Heat＆MassTransfer，2015，84：327－338.

［14］ Wei A，Tong Z，Naiping G.Accelerative iteration for coupled conductive－radiative heat transfer computation in semitransparent media ［J］.InternationalJournalofHeat andMassTransfer，2015，82：503－509.

［15］ Ait－Taleb T，Abdelbaki A，Zrikem Z.Simulation of coupled heat transfers in a hollow tile with two vertical and three horizontal uniform rectangular cavities heated from below or above ［J］.Energy＆Buildings，2014：628－632.

［16］ Chen Baodong（陈保东），Li Qingjie（李庆杰），Hong Lina（洪 丽 娜 ），Yue Chunguang （岳 春 光 ）.Calculation of transmission process parameters for LNG pipeline ［J］.Oil＆GasStorageandTransportation（油气储运），2011，30（1）：15－17.

［17］ Yang Shiming （杨 世 铭），Tao Wenquan （陶 文 铨）.Heat Transfer（传热学） ［M］.Beijing：Higher Education Press，2006：246－247.

［18］ Lai F C，Kulacki F A.Coupled heat and mass transfer by natural convection from vertical surfaces in porous media［J］.InternationalJournalofHeatandMassTransfer，1991，34 （4／5）：1189－1194.

［19］ Deru M，Judkoff R，Neymark J.Whole building energy simulation with a three－dimensional ground－coupled heat transfer model［J］.ASHRAE，2003，109 （1）：557－565.