二氧化碳在CH4＋CO2＋N2／C2H6三元系中的结霜温度计算

熊晓俊，林文胜

（上海交通大学制冷与低温工程研究所，上海200240）

引 言

当前，我国已探明的天然气气田中多数含有二氧化碳，如大庆的庆深气田、吉林气田、塔里木气田等。有些甚至是高CO2含量的气田，如东方1－1气田的CO2含量为20.28%，崖城13－1气田的CO2含量为7.65%，平湖油气田CO2含量为4%［1］。含CO2的天然气需要转变成管道气或液化天然气产品才能进入市场。对于边远气田或海上气田，无法采用管道输送，液化天然气便成为其进入市场的唯一方式。当这些含CO2的天然气历经低温工艺转变成－161℃［2］液化天然气产品时，由于CO2的三相点温度 （216.55K）较高，容易在低温工艺过程中凝华结霜产生固体CO2，造成分馏塔、换热器、膨胀机等关键设备的堵塞甚至损坏［3－4］，甚至引起停产并带来严重的经济损失。为此，对CO2在天然气中的结霜温度进行预测，就显得十分必要。

目前，国外已有一些学者针对CO2在天然气中的结霜温 度 进 行 了 实 验［5－8］和 理 论 计 算［6，7，9－11］的研究。显然，实验只能在特定的温度和压力工况下开展，得到的结果十分有限。相较而言，理论计算可以方便地涵盖较广的温度压力区间，因而是一种更有力的预测方式。Agrawal等［6］采用BWR状态方程对CO2在CH4－CO2二元系、CH4－CO2－N2三元系中的结霜温度进行了计算。ZareNezhad等［9］利用PR状态方程结合修正的CH4－CO2二元交互作用系数对CO2在CH4－CO2二元系中的结霜温度开展了计算。Zhang等［7］采用SRK状态方程对CO2在CH4－CO2二元系中的结霜温度做了计算。国内，熊晓俊等［10］在之前的研究工作中采用PR状态方程计算了CO2在CH4－CO2二元系中的结霜温度。蒋洪等［11］预测了 CH4－CO2体系固体CO2形成条件。由上所述，可以发现当前有关CO2在天然气中的结霜温度计算仍主要集中在CH4－CO2二元系，鲜有涉及三元及以上的多元天然气体系。天然气是由C1～C10等烷烃以及氮气、二氧化碳等气体组成的混合物，因而有关多元天然气体系的计算更具实际意义。为此，本文针对CO2在CH4－CO2－N2和CH4－CO2－C2H6三元系中的结霜温度进行了计算。此外，针对文献中已有的二元系数据，比较不同状态方程的计算结果相较于实验结果的精度，发现BWR状态方程的精度为0.39%［6］，PR状 态 方 程 为 0.23%［9］，SRK 状 态 方 程 为0.31%［7］，可知PR状态方程精度最高。故而，本文采取PR状态方程法对三元系中CO2的结霜温度进行计算。

除了PR状态方程法，本文还采用了道尔顿分压定律和HYSYS两种方法来计算CO2在CH4－CO2－N2和CH4－CO2－C2H6三元系中的结霜温度，并对3种计算方法的精度进行了比较，为生产实际提供指导。

1 计算方法

CO2在 CH4－CO2－N2和 CH4－CO2－C2H6三 元系中结霜，本质上是由于CO2发生了气固相变，故而，可根据气固相平衡的原理来计算CO2的结霜温度。从公开发表的文献中可以看出，基于气固相平衡原理的计算方法常用的都是状态方程法。于是本文也采用了PR状态方程法计算了CO2在CH4－CO2－N2和 CH4－CO2－C2H6三 元 系 中 的 结 霜温度。然而，由于状态方程形式复杂，求解烦琐，在工程应用上十分不便。为此，本文提出了一种简便的计算方法，利用道尔顿分压定律，结合气固相平衡的 原 理 来计 算 CO2在 CH4－CO2－N2和 CH4－CO2－C2H6三元系中的结霜温度。此外，本文还借助 HYSYS 软 件 计 算 了 CO2在 CH4－CO2－N2和CH4－CO2－C2H6三元系中的结霜温度。

1.1 PR状态方程法

根据气固相平衡的原理，建立的CO2的气固相逸度平衡方程，如式 （1）所示

式中，fv（CO2）和fs（CO2）分别为 CO2在三元系中的气相逸度和固相逸度。

在温度为T，压力为p，CO2摩尔分数为x（CO2）时，CO2在三元系中的气相、固相中的逸度可分别按式 （2）、式 （3）计算。

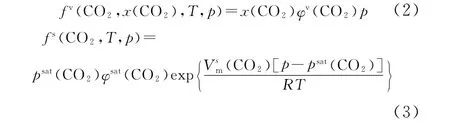
式中，φv（CO2）为CO2在三元系中的逸度系数；psat（CO2）为CO2的气固饱和蒸气压；φsat（CO2）为CO2在饱和状态下的逸度系数；Vsm（CO2）为固体CO2的摩尔体积，取值3.1428×10－5m3·mol－1［6］；R为气体摩尔常数，R＝8.3145J·mol－1·K－1。

混合物中某组分的逸度系数，可通过PR状态方程来计算，PR状态方程［12］如式 （4）所示

写成压缩因子z的立方形式，如式 （5）所示

其中

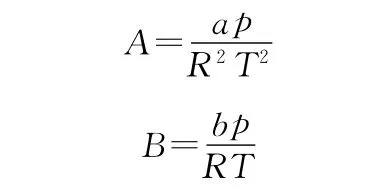
采用VDW混合规则［13］，其中

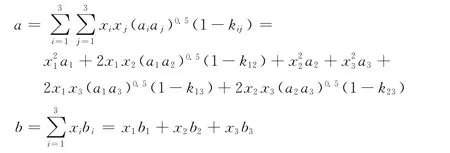
其中

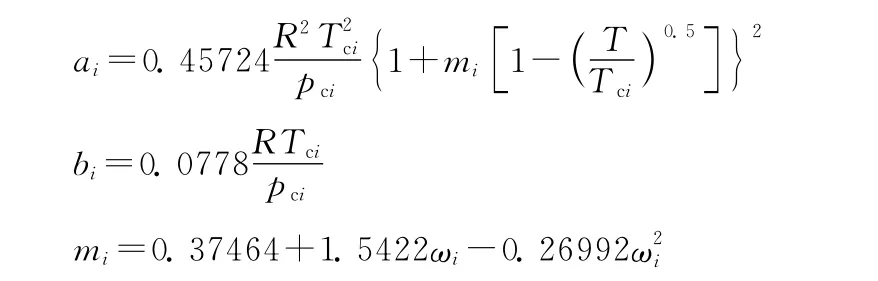
式中，xi表示混合物中组分i的摩尔分数；kij表示组分i和组分j的二元交互作用系数，三元系中两两组分之间的二元交互作用系数见表1［9，14－16］；Tci、pci和ωi分别表示组分i的临界温度、临界压力和偏心因子，三元系各组分的参数见表2［17］。

表1 各组分间的二元交互作用系数Table 1 Binary interaction parameter between components

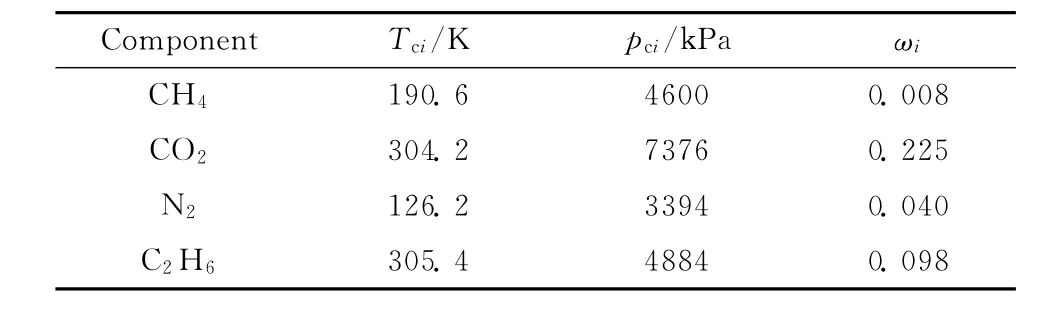
表2 各组分参数Table 2 Parameters of each component

将上述混合规则应用于PR状态方程，可求得混合物中组分i的逸度系数为

CO2在 CH4－CO2－N2和 CH4－CO2－C2H6三 元系中结霜，由于CO2的三相点温度远高于其他组分，故而可认为固相为纯CO2。对于纯固相CO2的逸度系数，可由式 （6）简化为式 （7）来计算

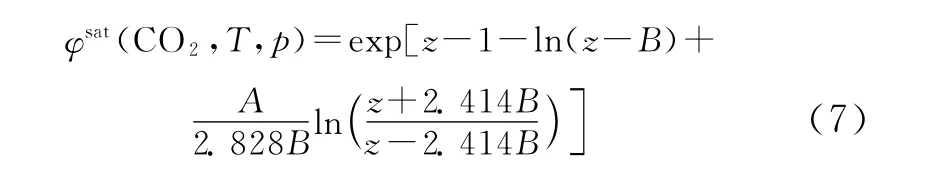
此外，从文献［9］中选取的CO2的气固相饱和蒸气压的拟合函数为

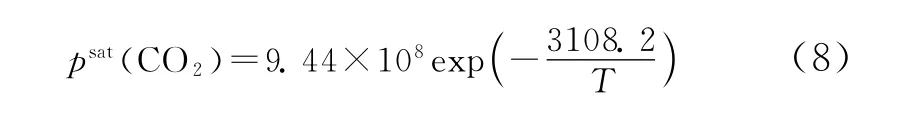
在已知压力p，组分xi的情况下，联立式 （1）～式 （8）求解，便可求出CO2在CH4－CO2－N2和CH4－CO2－C2H6三元系中的结霜温度T。

1.2 道尔顿分压定律法

由上述PR状态方程法的计算过程，可以看出该方法的计算较为烦琐，在工程应用中，通常更希望有一种简便快捷且准确的方法来计算。为此，本研究将 CH4－CO2－N2和 CH4－CO2－C2H6三元 系 视为理想系，根据道尔顿分压定律 （Dalton’s law of partial pressure）以及气固相平衡的原理来计算CO2的结霜温度。

根据气固相平衡的原理，建立的CO2气固相分压平衡方程，如式 （9）所示

式中，pv（CO2）为CO2在三元系中的气相分压；psat（CO2）为纯质CO2的气固相饱和蒸气压，如式 （8）所示。

根据道尔顿分压定律，CO2在三元系中的气相分压，可按式 （10）计算

联立式 （8）～式 （10），可求得CO2的结霜温度为

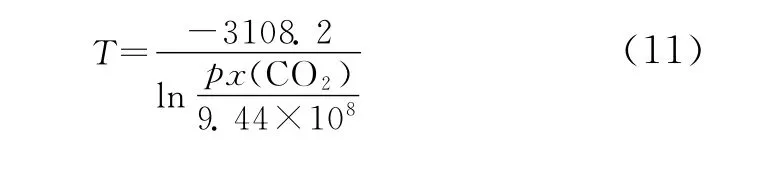
1.3 HYSYS法

HYSYS是石油天然气一类的化工行业广泛应用的模拟流程的软件［18－19］。它具有强大的物性数据包，以及许多便捷的计算工具包。HYSYS中的CO2Freeze Out工具包便可用来计算CO2结晶析出温度［20］。

在HYSYS中选择PR状态方程和数据库默认的二元交互作用系数来计算物性。HYSYS里的二元交互作用系数见表3。设置好物流的压力p和组分xi参数，然后使用CO2Freeze Out工具，便可得知 CO2在 CH4－CO2－N2和 CH4－CO2－C2H6三元系中的结霜温度T。

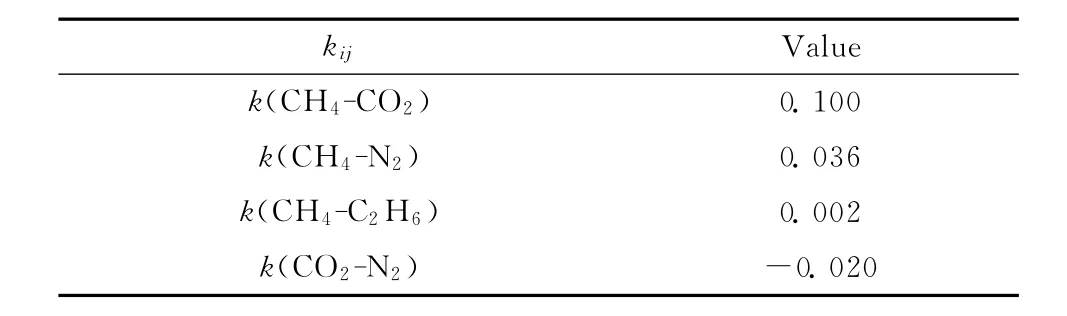
表3 HYSYS里的二元交互作用系数Table 3 Binary interaction parameter between components in HYSYS

2 计算结果与讨论

2.1 计算结果

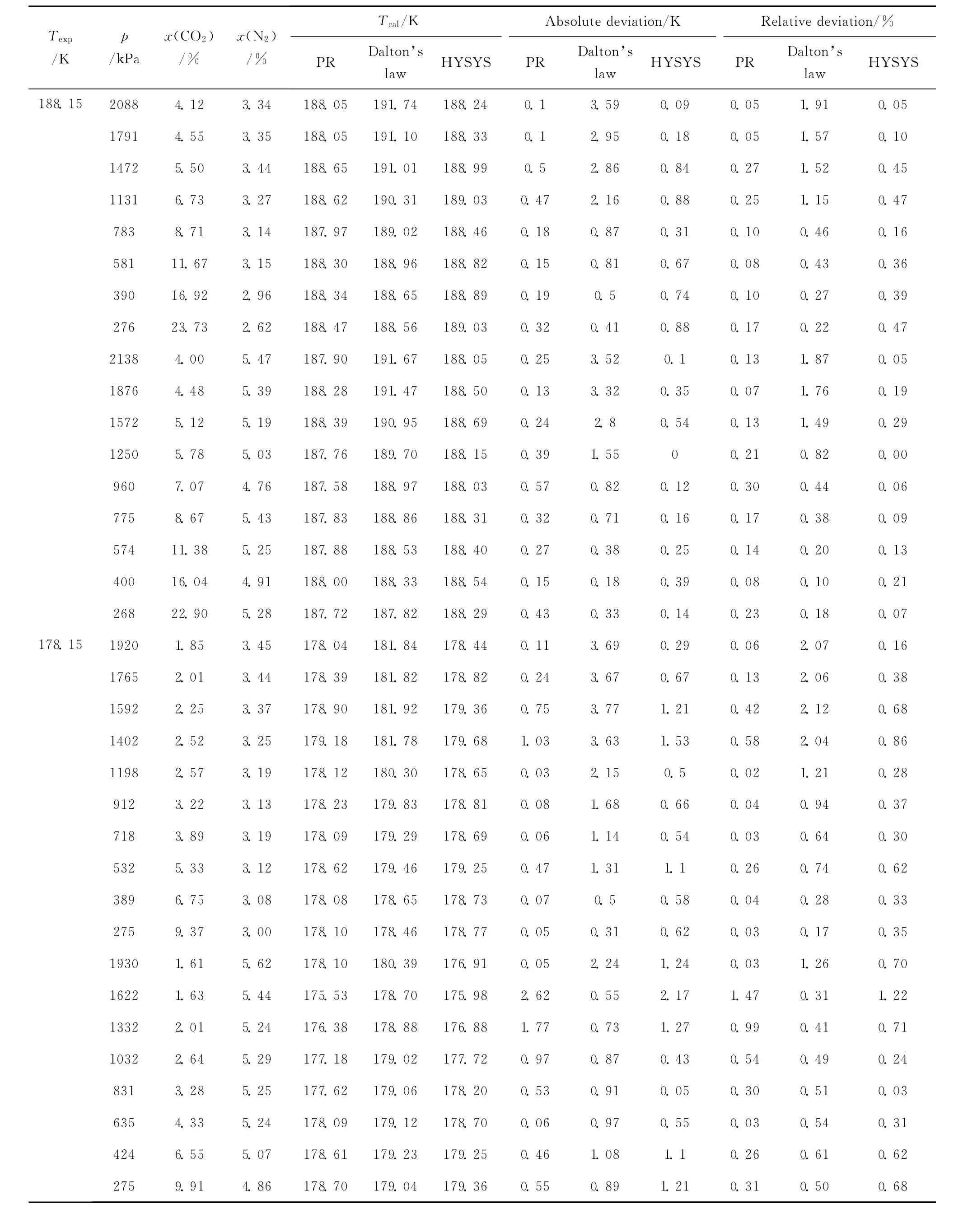
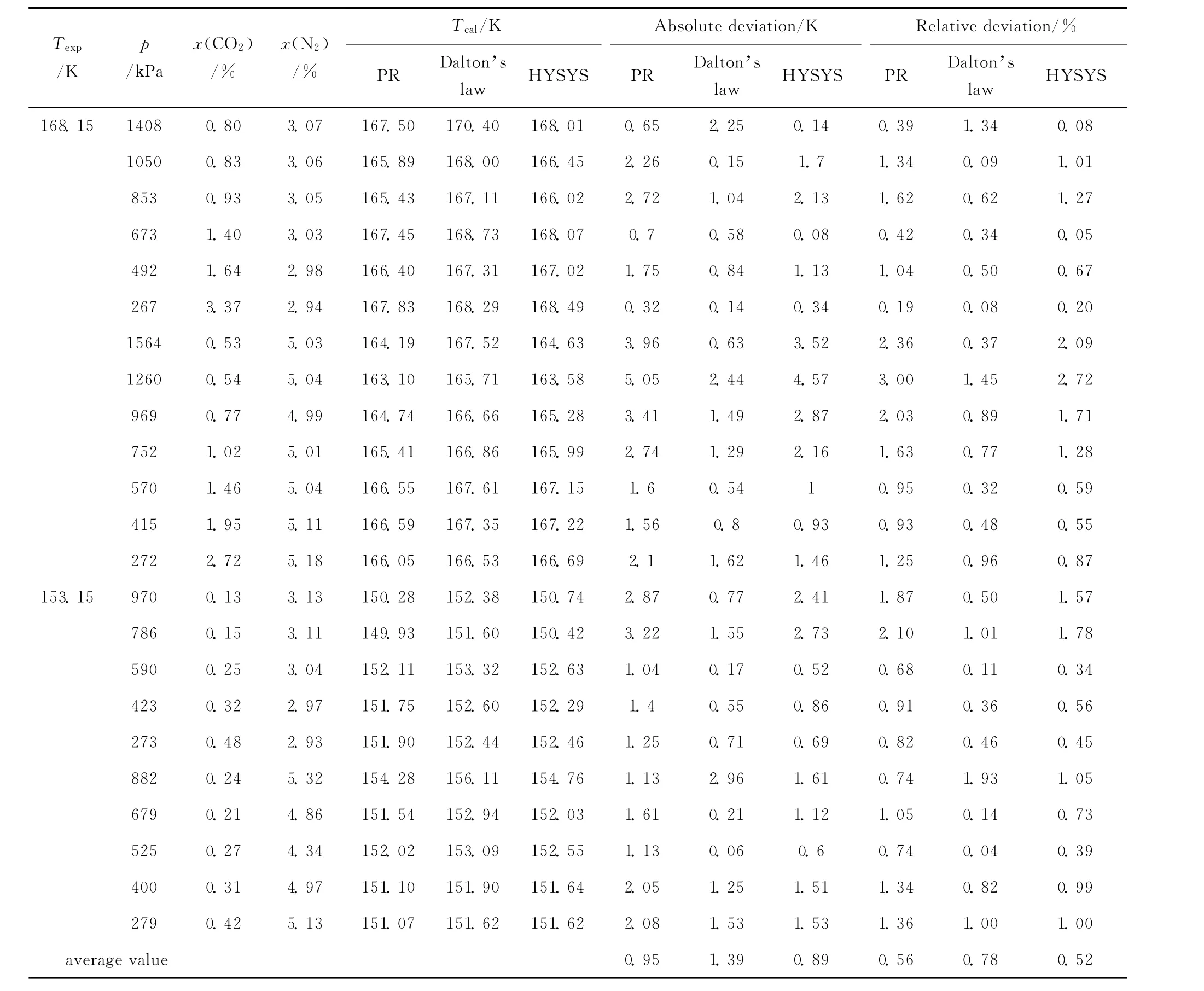
在之前的研究工作中，借助平衡釜实验装置，采用静态取样法，得到了 CH4－CO2－N2和 CH4－CO2－C2H6三元系在不同温度、压力、组分条件下的结霜实验数据［21］。本研究将这些实验数据作为衡量各计算方法精度的依据，列在表4、表5中。实验时，测量的是已知温度 （Texp）和压力下对应的结霜组分；计算时，采用与实验压力、组分相同的条件来计算对应的结霜温度 （Tcal）。依次利用PR状态方程法、道尔顿分压定律法、HYSYS法，对 CO2在 CH4－CO2－N2和 CH4－CO2－C2H6三元系中的结霜温度 （Tcal）进行计算，计算结果见表4、表5。以实验值作为比较标准，表4、表5还给出了3种方法计算结霜温度的绝对误差（absolute deviation） 和 相 对 误 差 （relative deviation）及其平均值 （average value）。其中，绝对误差和相对误差，分别按式 （12）、式 （13）来计算。

表4 CO2在CH4－CO2－N2三元系中的结霜温度Table 4 Frost point temperature of CO2in CH4－CO2－N2ternary mixtures

（Continued）

（Continued）

表5 CO2在CH4－CO2－C2H6三元系中的结霜温度Table 5 Frost point temperature of CO2in CH4－CO2－C2H6ternary mixtures

（Continued）

（Continued）

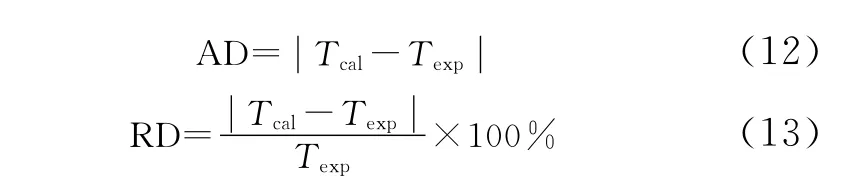
2.2 结果讨论

将表4和表5中PR状态方程法、道尔顿分压定律法、HYSYS法3种方法的计算值和实验值相比较，可以发现，3种方法的结果和实验值均吻合得很好。此外，由表4可知，当应用于CH4－CO2－N2三元系时，PR状态方程法、道尔顿分压定律法、HYSYS法的平均绝对误差分别为0.95、1.39、0.89K， 平 均 相 对 误 差 分 别 为 0.56%、0.78%、0.52%；由表5可知，当应用于 CH4－CO2－C2H6三元系时，PR状态方程法、道尔顿分压定律法、HYSYS法的平均绝对误差分别为0.68、1.87、0.97K， 平 均 相 对 误 差 分 别 为0.37%、1.02%、0.54%。3种方法的平均误差均较小，这表明3种方法均可作为预测CO2在三元乃至更多元天然气体系中的结霜温度的有效手段。其中PR状态方程法和HYSYS法的精度相近，二者均比道尔顿分压定律法精度更高。

为更进一步、直观地进行比较和分析，从表4和表5中选取部分典型的数据绘制成曲线，如图1和图2所示。其中，图1是选取CH4－CO2－N2三元系中Texp＝188.15K的一组数据绘制而成；图2是选取 CH4－CO2－C2H6三元系中Texp＝188.15K的一组数据绘制而成。

图1 针对CH4－CO2－N2三元系不同方法得出的结果Fig.1 Results by different methods for CH4－CO2－N2ternary mixture

图2 针对CH4－CO2－C2H6三元系不同方法得出的结果Fig.2 Results by different methods for CH4－CO2－C2H6ternary mixture

在图1和图2中，比较PR状态方程法和HYSYS法的计算结果，可以看出，不论是应用于CH4－CO2－N2还是 CH4－CO2－C2H6三元系，PR 状态方程法和HYSYS法的计算结果都比较相近，两者仅存在微小的差别。这是因为两者都选用PR状态方程进行物性计算。二者之间的微小差别，主要由二元交互作用系数的取值不同造成。由此可见，提高二元交互作用系数的准确性，将有利于提高状态方程法的计算精度。准确的二元交互作用系数，可通过实验数据来回归分析获得。由于目前相关实验数据十分有限，因而相应的数据分析工作仍有待完善。

在图1和图2中，比较道尔顿分压定律法的计算结果和实验值，可以发现，道尔顿分压定律法在低压时比高压时能获得更接近实验值的计算结果。这是 因 为 在 低 压 时，CH4－CO2－N2和 CH4－CO2－C2H6三元系更接近于理想系，此时采用适用于理想气体的道尔顿分压定律计算得到的结果自然更精确。由图1和图2可知，随着压力的升高，道尔顿分压定律法的误差也逐渐增大。虽然道尔顿分压定律法在高压时，精度不如PR状态方程法和HYSYS法高，但是该方法计算简单，可以用于工程上快速估算。

3 结 论

本研究采用了PR状态方程法、道尔顿分压定律法、HYSYS法3种方法来计算CO2在CH4－CO2－N2和 CH4－CO2－C2H6三元系中的结霜温度，得出了以下结论。

（1）PR状态方程法、道尔顿分压定律法、HYSYS法3种方法都能获得与实验相吻合的结果。三者的平均绝对误差都小于2K，平均相对误差都小于2%。

（2）PR状态方程法和HYSYS法的精度相近，且均高于道尔顿分压定律法。道尔顿分压定律法应用于低压区的精度高于高压区，且精度随着压力的升高而下降。

（3）虽然道尔顿分压定律法的精度不及其他方法，但该方法计算简便，且能获得满意的结果，可用于工程上的快速估算。

符 号 说 明

AAD——平均绝对误差

AD——绝对误差

ARD——平均相对误差

f——逸度，kPa

k——二元交互作用系数

n——数量

p——压力，kPa

R——气体常数，J·mol－1·K－1

RD——相对误差

T——温度，K

v——比体积，m3·mol－1

x——组分含量

z——压缩因子

φ——逸度系数

ω——偏心因子

上角标

s——固相

sat——饱和状态

v——气相

下角标

c——临界状态

cal——计算

exp——实验

i——组分i j——组分j

［1］ The Editorial Committee of Offshore Oil Engineering Design Guide（海洋石油工程设计指南编委会）.Design Introduction and Process Design of Offshore Oil Engineering：1st volume（海洋石油工程设计概论与工艺设计：第一册）［M］.Beijing：Petroleum Industry Press，2007：100.

［2］ Gu Anzhong （顾 安 忠 ） .Natural Gas Liquefaction Technology（液 化 天 然 气 技 术 ） ［M］.Beijing：China Machine Press，2004.

［3］ Chang H，Chung M J，Park S B.Cryogenic heat－exchanger design for freeze－out removal of carbon dioxide from landfill gas ［J］.J.Therm.Sci.＆Tech.，2009，4：362－371.

［4］ Eggman T，Chafin S.Beware the pitfalls of CO2freezing prediction ［J］.Chem.Eng.Prog.，2005，101：39－44.

［5］ Pikaar M J.A study of phase equilibrium in hydrocarbon－CO2systems ［D］.London：Department of Chemical Engineering，Imperical College of Science and Technology，1959.

［6］ Agrawal G M，Laverman R J.Phase behavior of the methane carbon dioxide system in the solid－vapor region ［J］.Adv.Cryo.Eng.，1974，19：327－338.

［7］ Zhang Longman，Burgass R，Chapoy A，Tohidi B，Solbraa E.Measurement and modeling of CO2frost points in the CO2－methane systems ［J］.J.Chem.Eng.Data，2011，56 （6）：2971－2975

［8］ Le T T，Trebble M A.Measurement of carbon dioxide freezing in mixtures of methane，ethane，and nitrogen in the solid－vapor equilibrium region ［J］.J.Chem.Eng.Data，2007，52 （3）：683－686.

［9］ ZareNezhad B，Eggeman T.Application of Peng－Rabinson equation of state for CO2freezing prediction of hydrocarbon mixtures at cryogenic conditions of gas plants ［J］.Cryogenics，2006，46：840－845.

［10］ Xiong Xiaojun （熊 晓俊），Lin Wensheng （林文胜），Gu Anzhong （顾 安 忠）.Prediction of CO2frosting temperature in CH4－CO2binary system ［J］.Chem.Eng.Oil＆Gas（石油与天然气化工），2012，（2）：176－178.

［11］ Jiang Hong （蒋洪），He Yuxin （何愈歆），Zhu Cong （朱聪）.Prediction of solid CO2formation condition in CH4－CO2system ［J］.Nat.GasInd.（天然气工业），2011，31 （9）：112－115.

［12］ Peng Dingyu，Robinson D B.A new tow－constant equation of state ［J］.Ind.Eng.Chem.Fundam.，1976，15：59－64.

［13］ Kwak T Y，Mansoori G A.van der Waals mixing rules for cubic equations of state.Applications for supercritical fluid extraction modeling ［J］.Chem.Eng.Sci.，1986，41 （5）：1303－1309.

［14］ Kidnay A J，Miller R C，Parrish W R，Hiza M J.Liquidvapor phase equilibrium in the N2－CH4system from 130to 180K ［J］.Cryogenics，1975，15 （9）：531－540.

［15］ Mazzoccoli M，Bosio B，Arato E，Brandani S.Comparison of equations－of－state withp－ρ－Texperimental data of binary mixtures rich in CO2under the conditions of pipeline transport ［J］.J.Supercrit.Fluids，2014，95：474－490.

［16］ Kordas A，Tsoutsouras K，Stamataki S，Tassios D.A generalized correlation for the interaction coefficients of CO2－hydrocarbon binary mixtures ［J］.FluidPhaseEquilib.，1994，93：141－166.

［17］ Bian Xiaoqiang，Du Zhimin，Tang Yong.Experimental determination and prediction of the compressibility factor of high CO2content natural gas with and without water vapor［J］.J.Nat.GasChem.，2011，20：364－371.

［18］ Gao Ting，Lin Wensheng，Gu Anzhong，Gu Min.Coalbed methane liquefaction adopting a nitrogen expansion process with propane pre－cooling ［J］.Appl.Energy，2010，87：2142－2147.

［19］ Aspelund A，Gundersen T，Myklebust J，Nowak M P，Tomasgard A.An optimization－simulation model for a simple LNG process ［J］ .Comp.Chem.Eng.， 2010， 34：1606－1617.

［20］ Hu Xiaochen （胡晓晨），Gao Ting （高婷），Lin Wensheng（林文胜）.Preliminary research on CO2freeze－out in PLNG process ［J］.Cryo.＆Supercond.（低温与超导），2009，37（6）：15－18.

［21］ Xiong Xiaojun，Lin Wensheng，Jia R，Song Yang.Measurement and calculation of CO2frost data in CH4＋CO2／CH4＋CO2＋ N2／CH4＋CO2＋C2H6mixtures at low temperatures ［J］.J.Chem.Eng.Data，（in press）.