直井短宽缝压裂产能计算

刘晓强，郭天魁，李小龙，周丽萍，许华儒，李建雄

（中国石油大学（华东）石油工程学院，山东 青岛266580）

老区油田井网三次加密后，注采井距成倍缩小，为防止裂缝与水井窜通，保持合理的穿透比，对储层的改造多采用密井网压裂工艺以形成短宽缝［1］。前期研究表明，垂直裂缝井渗流场中的等势线为椭圆形，并且满足流线与椭圆共焦的双曲线方程；但水电模拟实验表明，用短宽垂直裂缝井生产的油层，其地层中等势线分布从供油边界向井筒由圆形过渡为椭圆形，裂缝附近等势线为椭圆形，远离裂缝等势线为圆形。单一椭圆流理论不再适用于该种渗流场，要分2 部分进行描述，即外部的径向流和内部的拟径向流。

1 直井短宽缝压裂产能计算模型

1.1 基本假设

各向同性的均质油藏，恒压边界条件下不可压缩流体在地层中流动，垂直裂缝相对于低渗地层为无限导流能力；不考虑重力的影响；初始时刻地层压力处于平衡状态。

1.2 临界边界求解

利用该模型确定2 种渗流形态的边界，是问题求解的关键。在2 种形态的交界处，拟径向流形成的临界椭圆等压线与径向流形成的临界圆形等压线十分接近，本文采用等面积法进行近似求解。

假设油藏外边界为圆形，根据水电模拟实验得知，椭圆形等压线分布区域与裂缝半长有关。多次实验发现，内部圆形等压线与外部椭圆形等压线的分界区一般分布在半径为裂缝半长5 倍的圆形所在区域。临界圆形半径rd为

式中：xf为压裂后形成的垂直裂缝半缝长，m；C 为实验倍数值。

获得了径向流临界圆形半径后，通过采用等面积法进行处理，即临界圆形所围的面积与临界椭圆形所围的面积相等，来获得拟径向流临界椭圆形的边界值。

式中：a，b 分别为椭圆的长、短半轴，m。

结合直角坐标系与椭圆坐标系的关系，可以求出拟径向流的临界值ξd：

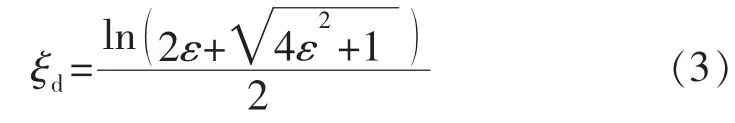
1.3 内部拟径向流

基于椭圆渗流理论对垂直裂缝井拟径向流动时的产能模型进行研究［2-9］，并且考虑了启动压力梯度。垂直裂缝井生产时，在裂缝附近某一区域的水平截面上，会形成等压椭圆柱面（见图2）。

图1 等压椭圆柱面流场

沿x 方向的垂直裂缝长度为2xf。当垂直裂缝井生产时，在裂缝周围压力的分布会形成椭圆面，直角坐标系与椭圆坐标系的关系为

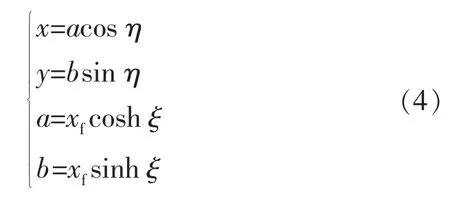
式中：η，ξ 为椭圆坐标系变量；x，y 为直角坐标系变量。

受地层渗透性和流体性质的影响，考虑流体在地层中流动存在着启动压力［10-13］。根据广义达西定律：

同时，信息网络涉及到国家的政府、军事、文教等诸多领域，存储、传输和处理的许多信息是政府宏观调控决策、商业经济信息、银行资金转账、股票证券、能源资源数据、科研数据等重要的信息。其中有很多是敏感信息，甚至是国家机密，所以难免会吸引来自世界各地的各种人为攻击（例如信息泄漏、信息窃取、数据篡改、数据删添、计算机病毒等）。因此，网络信息安全在每个国家基本上都会上升到国家安全层次。

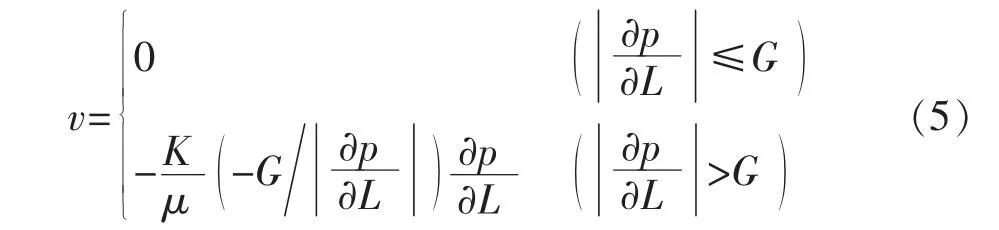
式中：v 为渗流速度，cm/s；K 为地层渗透率，μm2；μ 为原油黏度，mPa·s；G 为启动压力梯度，10-1MPa/m；L 为渗流方向坐标，m；p 为压力，10-1MPa。

基于椭圆渗流理论：

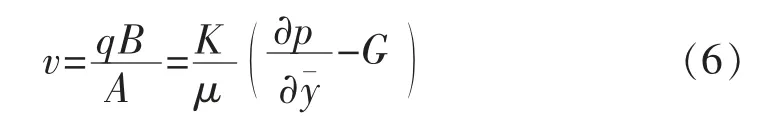
其中 A=4ah=4xfhcosh ξ

平均短轴为

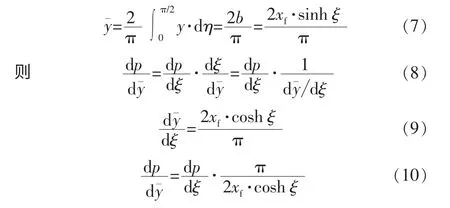
这样，式（6）可变形为

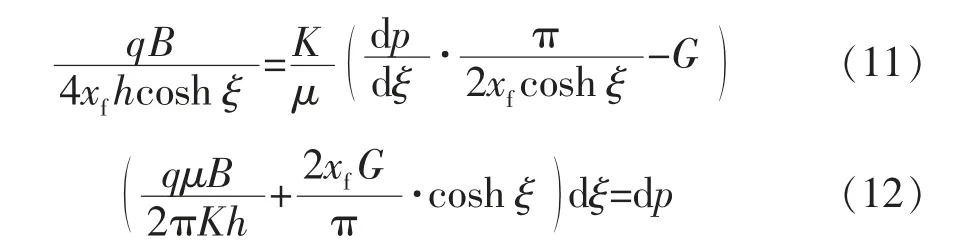
式中：q 为原油在地面条件下的体积流量，cm3/s；B 为原油体积系数；A 为渗流截面积，cm2；y¯为平均短轴，m；h 为油藏厚度，m。

将临界边界代入，对式（12）进行积分，得

进一步整理得到内部拟径向流部分流量：

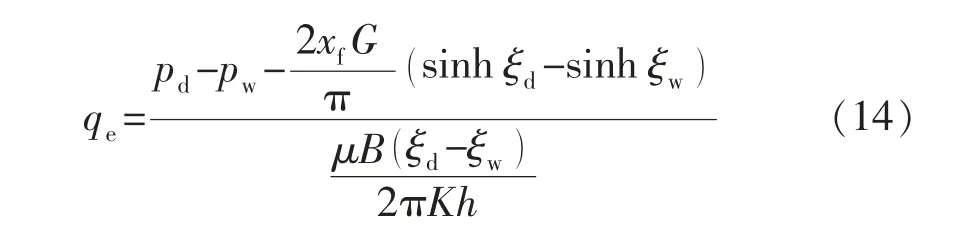
式中：qe为拟径向流部分流量，cm3/s。

内边界条件：

式中：rw为油井半径，m。

1.4 外部径向流

对于径向流部分，根据广义达西定律，得

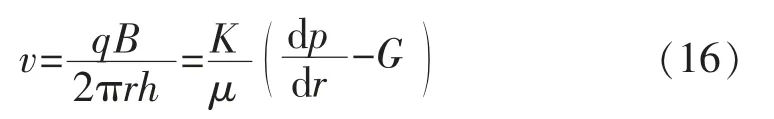
分离变量后得

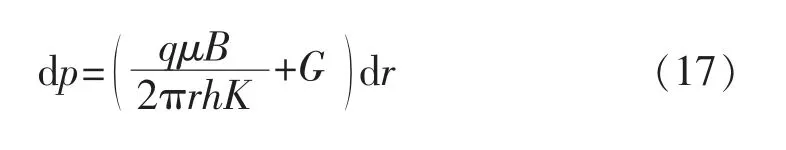
从外边界（re，pe）到2种流态临界处（rd，pd）对 式（19）进行积分，得到径向流部分流量：

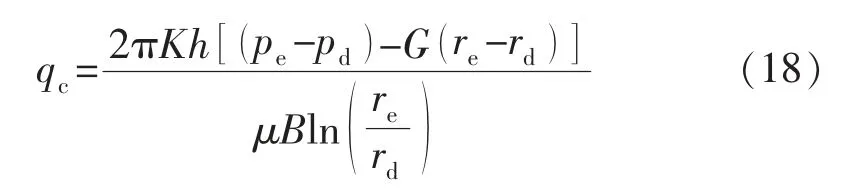
式中：qc为径向流部分流量,cm3/s；re为供油半径，m；pe为油藏边界压力，MPa。

根据质量守恒定律，得

这样，低渗油藏采用直井压裂形成短宽缝开发的产能公式为

2 水电模拟实验

2.1 实验原理

不可压缩流体通过地下多孔介质时，流动的微分方程与电荷通过导体流动时的微分方程具有相似性，这种水电相似性是水电模拟实验的理论基础［14］。在做水电模拟实验时，物理模型各参数与实际油藏相应参数之间存在一定的比例关系，为相似系数。水电模拟实验中包括几何相似系数、 压力相似系数、 阻力相似系数、流动相似系数、流量相似系数。

2.2 实验装置

水电模拟实验装置主要由4 部分组成。其包括油藏模拟装置、定点测量装置、低压电路装置和数据采集装置。

水电模拟实验中，油藏模拟装置采用有机玻璃板电解槽，选用的规格是1 500 mm×1 500 mm×400 mm。有机玻璃板电解槽具有绝缘性和隔离性，可以很好地模拟封闭油藏边界条件。紫铜带具有导电性，加上低压交流电后可以模拟供给边界。细铜丝具有导电性，而且方便改变铜丝的长度和直径，可以用来模拟井筒。对于油藏中的流体，选用一定浓度的CuSO4电解质溶液进行模拟，储层有效厚度即可通过控制电解质溶液的深度来实现。

2.3 实验结果

模拟某低渗油田，供油半径200 m，油藏厚度6 m，原始地层压力11.4 MPa，地层中原油黏度25 mPa·s，地层启动压力梯度0.001 MPa/m，地层渗透率50×10-3μm2。井底流压控制在4 MPa，模拟垂直裂缝井定压生产过程。

实验过程中，在供油半径一定的条件下，不断改变裂缝半长，记录油藏中各点的压力分布，并绘制出油藏中等势线分布的平面图。裂缝半长分别为15，20，30，40 m 时等势线分布如图2所示。

从图2可以看出，圆形边界油藏中间一口垂直裂缝井，在供油半径一定的前提下，随着裂缝长度的改变，油藏中等势线分布有所变化。当裂缝长度较短时，油藏中等势线分为2 部分，从供油边界向内某一半径位置处等势线以圆形分布，该位置与垂直裂缝井之间的等势线以椭圆形分布。

利用获得的电流值计算出地层中相应的流量，作为不同缝长下单井产量的实验值。用建立的数学模型对单井产能进行计算，获得了不同缝长时单井产量的理论值（见表1）。

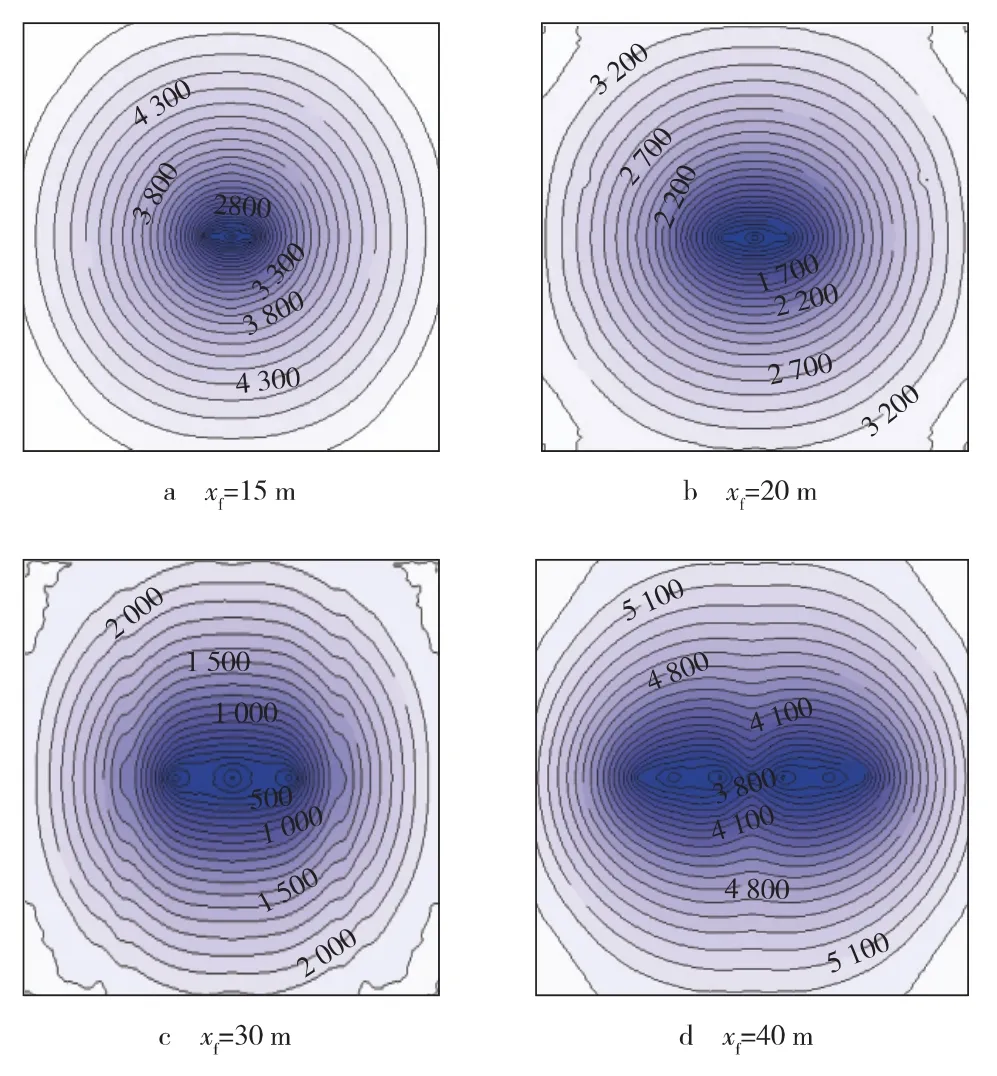
图2 不同缝长油藏等势线

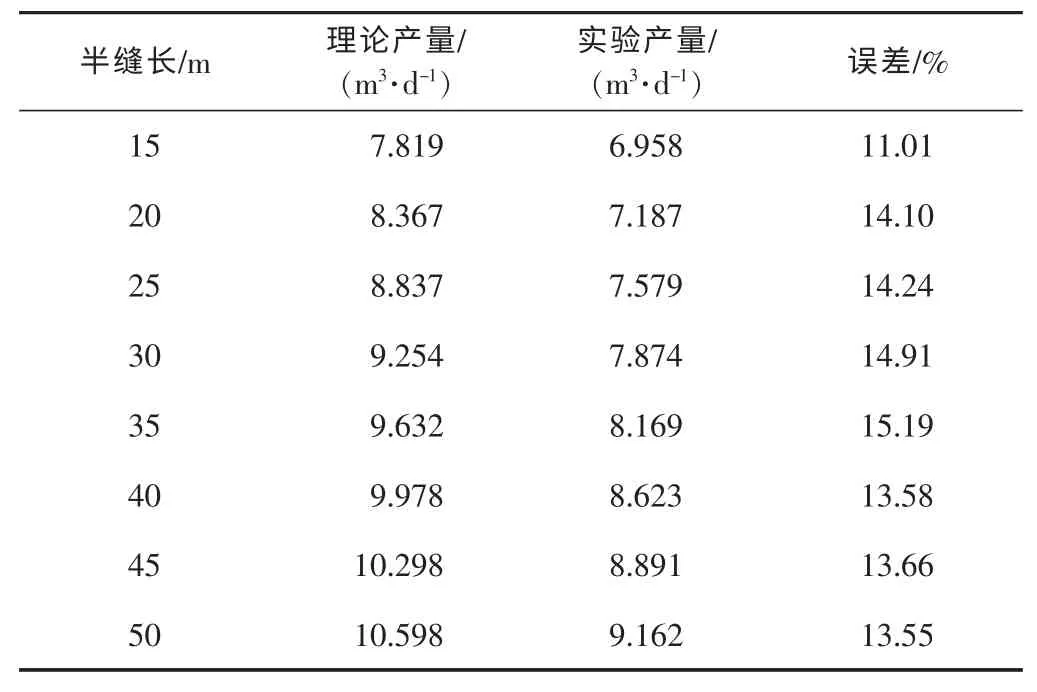
表1 不同缝长时单井理论产量和实验产量

从表1可以看出，通过水电模拟实验获得的直井短宽缝产能，与理论计算获得的产能相比，二者误差不足15%，满足工程上误差要求。这表明，本文提出的描述垂直井短宽缝的流动模型和据此得到的产能公式，具有一定的准确性和实际意义。

2.4 产能分析

利用产能公式分析了产能与裂缝半长和地层渗透率的关系（见图3）。可以看出，裂缝长度达到35 m 以后，长度对产能的影响减弱。对于直井压裂形成的短宽缝，其裂缝长度相对于供油半径本身就很短，少量增加裂缝长度对油井产能贡献不大，裂缝渗透率的增大，即导流能力的增大，可理解为裂缝宽度的增加，能显著提高油井产能。

所以在实际生产过程中，对于三次加密井需要采取压裂形成短宽缝的直井，如通过提高裂缝的宽度来改善导流能力，裂缝长度控制在供油半径的20%比较合理。

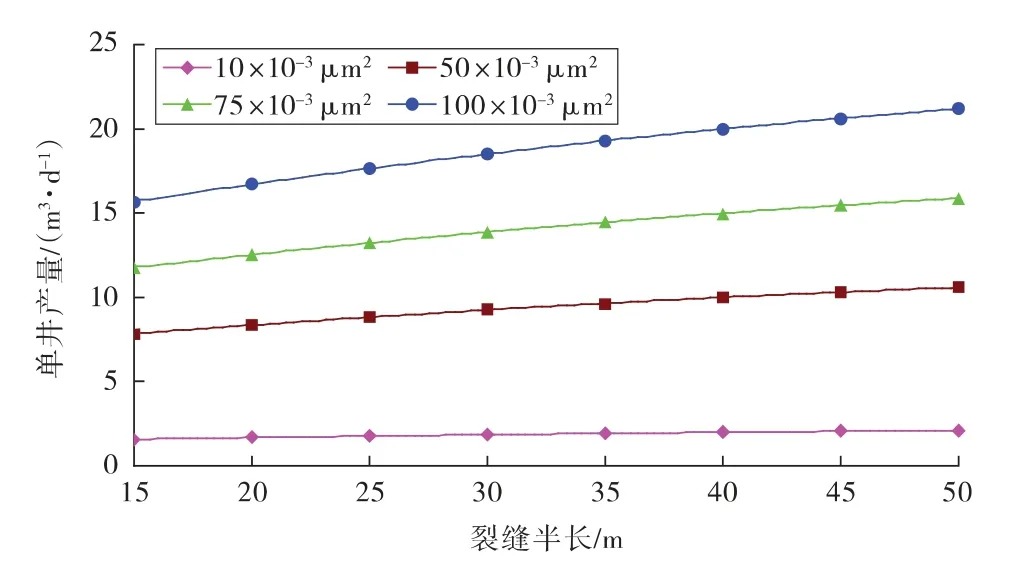
图3 半缝长和渗透率对产能的影响

地层流体黏度和半缝长对产能的影响（见图4）。油井产能随流体黏度的增加而迅速降低，特别是当流体为稠油时，流体黏度对油井产能有很大的制约作用，裂缝长度对油井产能的贡献很小。此外，低黏度时，油井产能随缝长增加而略有增加；高黏度时，缝长对油井产能的影响很小。

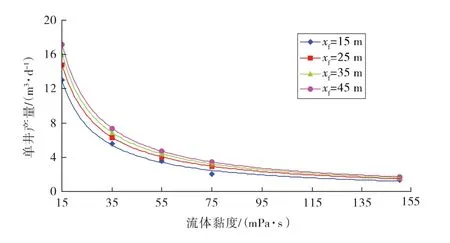
图4 流体黏度和半缝长对产能的影响

3 结论

1）水电模拟实验表明，直井压裂形成短宽缝时，油藏中等势线分为2 部分。从供油边界到油层内部某位置处等势线是以圆形分布，该位置与垂直裂缝井之间的等势线是以椭圆形分布；以井筒为圆心，5 倍裂缝半长为半径的圆形可作为区分2 种流动型态的边界。

2）利用椭圆渗流理论和平面径向流理论，针对地层流体向短宽缝流动的型态，将地层中的渗流分为径向流和拟径向流2 个区域，建立了考虑地层启动压力梯度的垂直井压裂形成短宽缝的产能计算模型。

3）直井短宽缝压裂产能受裂缝导流能力的影响程度远高于缝长。对于三次加密井需要采取压裂形成短宽缝的直井，缝长应控制在供油半径的20%。

［1］胡博仲，张有才，相荣成，等.短宽缝压裂工艺技术的研究与应用［J］.石油钻采工艺，1998，20（5）：89-94.

［2］刘英宪，高红立，张俊，等.非均质低渗油藏压裂井产能及动用半径研究［J］.复杂油气藏，2012，5（3）：53-55.

［3］李生，李霞，曾志林，等.低渗透油藏垂直裂缝井产能评价［J］.大庆石油地质与开发，2005，24（1）：54-60.

［4］Pertain A，Crunze M.Water-graphite interaction and behavior of water near the graphite surface［J］.The Journal of Physics Chemistry：B，2004，108（4）：1357-1364.

［5］Riley M F，Brigham W E，Horne R N，et al.Analytic solutions for elliptical finite-conductivity fractures［R］.SPE 22656，1991.

［6］Prats M.Effect of vertical fractures on reservoir behavior -incompressible fluid case［J］.Society of Petroleum Engineers Journal，1961，1（2）：105-118.

［7］陈德民，杨龙，苏富林，等.有限导流垂直裂缝井稳态渗流解析解及产能分析［J］.特种油气藏，2006，13（4）：62-64.

［8］缪飞飞，刘军令，任晓娟，等.低渗透油藏垂直裂缝井的产能分析［J］.重庆科技学院学报：自然科学版，2009，11（3）：40-42.

［9］何勇明，李爱芬，陶军，等.塑性流体型稠油油藏垂直井产能预测公式［J］.油气地质与采收率，2003，10（5）：57-59.

［10］田冀，许家峰，程林松，等.普通稠油启动压力梯度表征及物理模拟方法［J］.西南石油大学学报：自然科学版，2009，31（3）：158-162.

［11］杨仁锋，姜瑞忠，孙君书，等.低渗透油藏非线性微观渗流机理［J］.油气地质与采收率，2011，18（2）：90-97.

［12］甘庆明，成珍，成绥民.低渗油藏非达西流启动压力梯度的确定方法［J］.油气井测试，2004，13（3）：1-4.

［13］许家峰，程林松，李春兰，等.普通稠油油藏启动压力梯度求解方法与应用［J］.特种油气藏，2006，13（4）：53-57.

［14］杨阳，曲占庆，曹砚峰，等.径向井远端压裂电模拟实验研究［J］.断块油气田，2014，21（3）：386-389.