不定积分的求解方法*

张友梅，唐绍霞

(合肥职业技术学院，安徽 合肥 238000)

不定积分的求解方法*

张友梅，唐绍霞

(合肥职业技术学院，安徽 合肥 238000)

不定积分是高等数学的重要内容之一，其运算是微分运算的逆运算，但比微分运算困难得多.结合例题，分析不定积分解法的多样性与灵活性.

不定积分；被积函数；代换；解题

计算不定积分有多种方法,常见的有换元积分法和分部积分法,此外还有万能代换法、方程组法和待定系数法等,每一种方法既相互独立,又交叉联系,灵活多变.

1 换元积分法

换元积分法是指利用变量代换使积分化为可用基本积分公式求解积分的方法，它分为第一换元法和第二换元法.

1.1 第一换元法

第一换元法又称为凑微分法,解题思路是:通过选择一个适当的函数,作为新的积分变量来改变原积分被积式的结构,使其成为基本积分公式中已有的形式或便于求解的积分[1]，从而求出结果.具体解题步骤为．

第一换元法共分四步：凑微分、换元、积分、回代，关键是第一步如何“凑微分”,通常分析被积函数的特点,选择被积函数中的一部分进行凑微分,化为与基本积分公式相似的类型,然后进行变量代换,即可求解.

解法一(第一换元法)

解法二(直接积分法)

从上例可以看出，本题可以用多种方法求解,显然用第一换元法解题比直接积分法解题更为简洁.

1.2 第二换元法

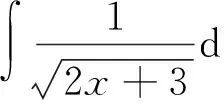
使用无理代换、三角代换,思维简单,但最后必须回代.而凑微分法,熟练解题之后,换元、回代过程可以省略,书写简洁.

2 分部积分法

因此有

即

3 万能代换法

解法二(凑微分法)

用不同的方法求不定积分时,得到的结果在表达形式上可能不相同,但至多相差一个常数,本质上是一致的.

4 方程组法

为了求某个不定积分I1,根据被积函数的特点,先构造另一个不定积分I2,使得I1与I2的线性组合积分mI1+nI2与mI1-nI2容易求出,然后联立方程组解出I1与I2,此方法称为方程组法.

I1+I2=ln|sinx-cosx|+C1

(1)

(2)

由(1)、(2)联立得

因此

本题也可用万能代换法,解法繁琐,从略.

5 待定系数法

对于复杂有理函数的积分,当被积函数分项较困难时,可采用待定系数法将有理函数分解成多个最简分式之和,然后逐一求解.

1=(A+E)x5+(B+F)x4+
(A+C)x3+(B+D)x2+Cx+D，

比较系数得

A=0，B=-1，C=0，D=1，E=0，F=1，

故有

解法三(三角代换法)令x=tant,则dx=sec2tdt,于是

可见，不定积分解法是灵活多变的,同一题目可能有多种解法,多个题目可能有统一解法,但任何一种积分方法,都是通过各类变换,把一个复杂的积分转化为基本积分公式的类型,然后求解.

[1]陆庆乐,陆诗娣.高等数学习题详解[M].北京:高等教育出版社,1998.

[2]孙法国.高等数学(上)导教·导学·导考[M].西安:西北工业大学出版社,2006.

[3]韩振芳.谈不定积分中的倒代换法[J].张家口师专学报,1996(2):31-35.

[4]同济大学数学系.高等数学[M].北京:高等教育出版社,2003.

[5]随如彬.微积分(经管类)[M].北京:科学出版社,2012.

[6]胡佳媛.用万能代换法求三角函数不定积分的不足[J].萍乡高等专科学校学报,2010,27(6):5-8.

(责任编辑:陈衍峰)

10.13877/j.cnki.cn22-1284.2015.04.011

2014-10-16

安徽高校省级质量工程项目“高等数学精品资源共享课程”(2013gxk161);合肥职业技术学院质量工程项目“高等数学精品资源共享课程”(JPKC201302)

张友梅,女,安徽巢湖人,讲师.

O171

A

1008-7974(2015)02-0029-03