递推SOM神经网络在短时交通流预测中的应用

黄 杰 李 军 郭 翔

(兰州交通大学自动化与电气工程学院1，甘肃 兰州 730070;青藏铁路公司2，青海 西宁 810000)

递推SOM神经网络在短时交通流预测中的应用

黄 杰1李 军1郭 翔2

(兰州交通大学自动化与电气工程学院1，甘肃 兰州 730070;青藏铁路公司2，青海 西宁 810000)

针对短时交通流预测，提出递归自组织映射(SOM)神经网络方法。根据SOM神经网络的联想记忆技术，分别给出考虑了反馈的RecSOM模型和能够利用结构化信息的SOMSD模型。递推SOM方法用全SOM作为重复神经元，用历史活动与当前信息的组合作为输入，通过训练神经元的权值及上下文信息学习时序动态。将递推SOM方法应用于预测某地区实测交通流数据，并与现有方法进行比较。试验结果表明,递推SOM方法能有效改善预测精度，在同等情况下优于其他方法。

短时交通流 智能交通 自组织映射 神经网络 递推 预测

0 引言

目前，智能交通系统(intelligent transportation systems,ITS)已有长足发展，但拥塞控制等问题仍难以解决，预测交通流有助于相关部门或者个人掌握交通趋势，选择最佳出行路径。先进交通控制系统(advanced traffic management systems,ATMS)也可根据预测值采取前瞻性措施，计划交通路线的最佳组合，实现拥堵控制。

在交通流预测领域，为了有效表达交通流量的不确定性和时变性，机器学习方法已成为主流预测手段。文献[1]采用小波神经网络实时预测交通流，文献[2]采用非参数回归算法预测短时交通流。文献[3]采用最小最大概率回归机(minimax probability machine regression,MPMR)网络实现短时交通流预测。文献[4]采用监督的在线加权学习算法预测短时交通流，均取得了较好的预测效果。可以看到，关于短时交通流预测的研究大部分采用监督学习神经网络。但在实际应用中，由于监督信息常常无法或者很难获得，因此发展非监督模型日趋重要；且由于交通流数据量一般较大，因此可处理结构化信息的网络更受青睐。

1 递推SOM预测方法

完全非监督自组织映射(self-organizing map,SOM) 神经网络[5-6]是芬兰Teuvo Kohonen教授提出的一种完全非监督竞争学习型神经网络。其构造简单直观、拓扑保持能力、输出可视化等优点已在机器学习领域引起关注。另外，SOM拓扑保持的全局性也避免了许多神经网络方法容易陷入局部最优的问题。

基于SOM神经网络的拓扑保持映射的能力，将SOM神经算法与递推思想相结合，所构建的递推SOM预测方法能进一步提高预测精度，包括RecSOM(recursive self-organizing map)和SOMSD(SOM for structured data)两种预测模型。这两种预测模型的区别在于对上下文向量(context vector)的表示不同。RecSOM模型用带时延的反馈表现递推的概念，SOMSD模型利用获胜神经元的网格坐标表示上下文信息，更适用于结构化数据。

将递推SOM方法应用于短时交通流预测实例中，在同等条件下，与现有的反向传播(BP)神经网络、支持向量机(SVM)等方法的预测结果进行比较，以验证所提出方法的有效性。

相对于SOM仅依据当前输入实现预测，递推SOM方法不仅考虑当前输入，也考虑历史信息。根据SOM的联想记忆技术，递推SOM方法用历史活动与当前信息的组合作为网络输入，存储了输入向量在大小、方向上的变化，一定程度上弥补了用窗函数方法处理数据时连续向量之间上下文信息的丢失。

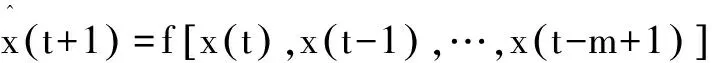
(1)

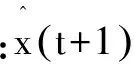
利用SOM网络逼近具有输入-输出特性的非线性映射，网络的输入向量x(t)∈G定义为两部分，包括模型输入xin(t)和预测输出xout(t)：

(2)

(3)

定义SOM输出平面的状态表示为y(t)∈G，则输出平面状态的不断变化呈现为相继的y(t)。为了保证历史活动的影响力，递推SOM方法的训练算法中对获胜神经元的选择考虑了上下文的影响。

令y=[y(t)…y(t-p)]，p为任意长度。当前输入x(t)对应的输出y(t)的上下文为yold=[y(t-1)…y(t-p)]。

将神经元i的权值向量表示为wi，递推SOM的广义输入包括xin(t)和对上下文yold的表示两部分，SOM平面上的每个神经元i的权值对应有wix与wiy两部分：

(4)

wix划分为wiin和wiout两部分，其中wiin为网络输入xin对应的权值；wiout为预测输出xout对应的权值。

令i*(t)表示获胜神经元，SOM用欧式距离最小来确定网络输入与权值wiin的最优匹配：

(5)

式中：d=‖xin(t)-wiin(t)‖为欧氏距离；t为与算法迭代响应的离散时间步。

递推SOM方法考虑了上下文yold，而调整距离函数改称为递推距离drecursive，以示与SOM区别。递推SOM方法按递推距离最小确定获胜神经元[7]：

(6)

上下文信息yold影响了获胜神经元的确定，被视为表现了获胜神经元间的转移。当y(t)对应的上下文yold与前一时间步的获胜神经元的坐标相似时，则该神经元更可能获胜。

特别地，递推SOM用全SOM作为重复神经元来表现上下文信息，方法的距离计算不仅考虑单个神经元的上下文信息，而且考虑整个映射平面的历史活动。这种表现递推的形式是自我参照的，体现了对自身活动的归类。

为了计算距离，针对上下文信息yold，令序列的上下文表示(contextrepresentation)为C(yold)。虽然RecSOM模型与SOMSD模型的C(yold)不同，但递推距离函数可统一表示为：

(7)式中：wiy为上下文所对应的权值；α与β为标量参数。

RecSOM模型与SOMSD模型的上下文表示C(yold)分别为CRecSOM(yold)与CSOMSD(yold)。由于上下文信息影响了对输入权值xin和上下文表示C(yold)的训练与更新，递推SOM方法使相似的输入选择了邻近的获胜神经元。

RecSOM模型用时延反馈表现递推概念，上下文表示存储了前一时间步的所有距离值，是一个|n|维向量：

(8)

式中：|n|为映射平面的神经元数目。

任意时间步的上下文表示都需要递推计算映射中每个神经元的递推距离，导致了非常复杂的获胜神经元选择机制。

SOMSD模型利用信息压缩处理结构化数据，是历史活动的低维表示，用前一时间步的获胜神经元的网格坐标gi*表示上下文信息：

(9)

递推SOM网络训练完成后，预测输出值为wiout(t)，即对应xout(t)的权值部分：

(10)

1.1 RecSOM模型

为了改进预测精度，文献[9]给出了一种用时延反馈来表现递推概念的策略，与SOM算法结合得到RecSOM模型。模型在保持SOM全部特性的基础上采用递推连接，且递推连接与前向连接均等，考虑了交通流量数据的时序性。通过合并当前输入和历史活动来表示时间的方法是自我参照的，体现了映射对自身行为的学习归类以及对数据历史活动的理解。

RecSOM模型是SOM算法在当前输入x(t)与前一时间步状态y(t-1)上的迭代表示，如图1所示。图1中，虚线表示可训练的连接，连续的箭头表示固定的一对一连接；黑色圆圈表示SOM在t时刻计算得出的获胜神经元，灰色圆圈表示在(t-1)时刻的获胜神经元，白色圆圈表示神经元，构成SOM神经网络的输出拓扑。具体方法是将当前输入与SOM输出平面之前的状态联系起来，共同作为网络输入，学习交通流量信息中隐含的规律。因此，每个神经元响应一系列输入。

图1 RecSOM的拓扑结构

将当前输入x(t)和上下文yold|p=1=y(t-1)共同作为对传统SOM算法的输入，映射单元需要学习一对数据(输入，上下文)的表示。

模型通过计算递推距离最小确定获胜神经元。分别计算映射神经元i的权值向量wiin和wiy与网络输入xin(t)和上下文向量y(t-1)的欧氏距离，其中，wiin为wix中网络输入xin对应的权值。按照前向连接与反馈连接是均等的，构建递推距离为：

(11)

前向权值和递推权值同时更新：

(12)

(13)

拓扑领域用高斯表示，完成量化：

(14)

为了保证权值向量收敛到稳定状态，学习率η(t)与邻域函数有效宽度σ(t)>0随时间的增加而逐渐衰减，可选用指数衰减的形式，如下：

(15)

(16)

式中：η0与ηT分别为学习率η(t)的初值与终值；σ0与σT分别为邻域函数有效宽度σ(t)的初值与终值；T为算法训练的迭代次数。

由于RecSOM模型加入了反馈，因此需要考虑网络在学习过程中的稳定性，权值的期望值需在学习过程中收敛。神经元i的上下文yi表示为：

(17)

由于反馈连接的转换函数决定了RecSOM模型的稳定性，依据经验选择转换函数如下：

(18)

转换函数连续且取值在0到1之间。针对匹配单元，函数值接近于1，高斯拓扑形式保证在输入、权值或者历史活动中的扰动都不影响匹配单元的稳定性。针对不匹配单元，函数值接近于0，因此，无论处于何种状态，模型始终稳定。

1.2 SOMSD模型

许多自然或人工系统利用数据结构实现更精确地建模，数据的结构化表示包含更大的信息量。为了处理编码为标记的有向无环图(directed acyclic graphs,DAGs)的结构化信息，Markus Hagenbuchne[10]等人提出SOMSD方法以处理结构化数据。该方法在完成结构化目标向拓扑平面映射的同时能找到输入间的相似性，递推学习过程加强了对模式分类的识别能力。在输入结构的拓扑映射中，神经元的空间位置表现了结构的统计特征。

针对短时交通流预测构建SOMSD模型，主要的创新点在于将获胜神经元的坐标作为下一时间步的上下文信息，且将上下文信息视为SOM的标准输入。也就是说，预测模型利用SOM的数据压缩能力采用前一时间步的获胜神经元的网格坐标gi*表示上下文信息。利用SOM的拓扑保持特性训练神经元权值及上下文信息，在相似性标准下聚类数据，即可诱导出模型对输入空间的度量。

SOMSD模型的递推距离函数为：

(19)

SOMSD模型中，权值wix的更新与RecSOM模型相同，见式(12)。类似地，上下文对应的权值wiy的更新为：

(20)

式中：gold=CSOMSD(yold)为之前时间步的获胜神经元的网格坐标。

相对于RecSOM模型需要设定反馈的转换函数这样较为复杂的获胜神经元选择机制，SOMSD模型用网格坐标gi*表示上下文的信息压缩手段确保了更快的处理速度。由于模型中的上下文信息是对历史活动的低维表示，因此SOMSD模型是降低复杂度的压缩模型。虽然压缩效果有效降低了模型运行时间，但SOMSD在实例中的预测精度与RecSOM持平。

针对树状结构数据研发的SOMSD方法，可将标号转化为一系列固定大小的向量。模型尝试在输入数据的权值及上下文向量中识别隐存的规律，映射平面通过返回获胜神经元的坐标表示对信息的压缩描述，如图2所示。

图2 对输入的递推映射举例

图2中，黑色区域表示在t时刻的获胜神经元，灰色区域表示在(t-1)或(t-2)时刻的获胜神经元。在图2(a)中，节点3数据输入映射平面,获胜神经元坐标为(2,2)。用此信息来表示节点2的输入向量，得到获胜神经元坐标为(0,1)，如图2(b)所示；最后将全部信息输入映射平面，获胜神经元坐标为(1,0)，如图2(c)所示。

1.3 算法描述

1) 数据预处理与网络初始化。

① 将数据划分为训练集与测试集，确定输入的维数，构建网络的输入输出。

② 初步确定网络的神经元拓扑，分别初始化权值wix和wiy，以及上下文向量C(yold)。

2) 网络的迭代训练。

① 顺序代入输入向量，利用权值向量wiin和wiy计算递推距离函数drecursive并确定获胜神经元i*(t)，其中t为时间步。

② 利用RecSOM的反馈连接转换函数或SOMSD的信息压缩手段计算上下文向量C(y)。

③ 通过计算映射平面其他神经元与获胜神经元的距离，分别更新权值向量wix和wiy。

④ 迭代直至输入数据按顺序代入完毕，网络训练结束，得到预测输出为wiout(t)，即xout(t)对应的权值部分。

3) 调整模型参数，直至预测精度达到最优，算法结束。

2 交通流预测实例分析

将递推SOM方法用于交通流预测实例，采用相空间重构方法处理数据，用互信息法确定时间延迟，用CAO方法确定嵌入维数。

作为对预测方法整体表现的衡量，选用均方误差(meansquareerror,MSE) 、正则化均方误差(normalizedmeansquareerror,NMSE)两种评估标准：

(21)

(22)

2.1 预测模型参量的选取

为了完成对数据分布的探索，SOM神经网络的神经元数目一般较大。如果神经元数目过少，部分聚类结果会因为异常值的存在而不精确，但若神经元数目偏多，则总有一部分神经元始终不被选中，导致神经元利用率偏低。不过，正是网络中没有用到的这些神经元提高了模型的泛化能力。试验结果显示，神经元利用率与数据集大小成反比，当SOM网络的神经元数目选为数据集大小的三分之一时，网络的学习效果最佳。

SOM算法要求领域半径初始值取得较大，以降低陷入局部极小的可能，而试验显示在一段范围内，递推SOM模型的邻域半径初值取得较小时预测效果更好。因为递推SOM模型依据节点类型聚类输入数据，聚类结构在训练初期就已经建立，之后聚类位置仅有微小改变，且主要更新发生在聚类内部。邻域函数半径取较小值，可使网络训练集中在较小的区域内；半径取较大值时表现出干扰的效果。

最后，针对网络迭代次数的问题，递推SOM网络的预测精度表现为随迭代次数的增加稳定上升，但超过一定阈值后就开始下降，反映了网络泛化能力会由于“过拟合”效应而降低。

2.2 实例一

实例一选取了英国某地区交通局的交通数据，观测时间为2011年3月,时间段为6∶00～20∶00，时间间隔取15min。本例中截选了交通流量序列的336个时间点。时间延迟τ=2，嵌入维数m=3。递推SOM神经元结构为15×15，σ=16，α=323，β=1，η=0.5。

实例一不同方法预测结果比较如表1所示，图3为在数据集上SVM、SOM、递推SOM模型预测值与实际值的对比。

表1 实例一不同方法预测结果比较

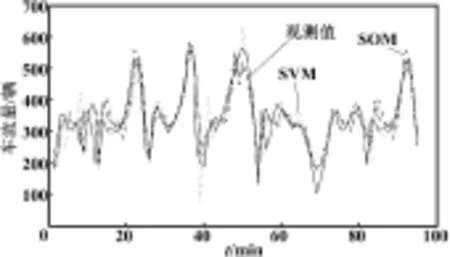
图3 实例一交通流量预测曲线

2.3 实例二

实例二的数据集来源于西雅图华盛顿大学ITS研究组的交通数据采集与分布(traffic data acquisition and distribution,TDAD)数据库，其网络站点为：www.its.washington.edu/tdad/，站点提供西雅图地区探测器所记录的交通流量值。本例选择探测器ES-088D记录的数据[11]，采集数据的时间为2005年6月6日至7月3日，时间间隔取为15 min，将交通流量数据处理为序列，共2 688个数据点。时间延迟τ=1，嵌入维数m=10。递推SOM方法的神经元结构为25×25，σ=60，α=323，β=1，η=0.5。

实例二不同方法预测结果比较如表2所示，图4为在数据集上SVM、SOM、RecSOM、SOMSD方法的预测值与实际值的对比。

图4 实例二交通流量预测

方法MSENMSE BP407．10910．0311 RBF369．85930．0290 SVM332．61250．0262 SOM362．78210．0286 RecSOM324．20570．0256 SOMSD327．55950．0258

由表1、表2所示，在相同条件下，采用本文方法与BP神经网络方法、RBF神经网络方法、SVM方法构建的预测模型比较结果可以看出，递推SOM预测方法精度最高。由图3、图4所示交通流量预测曲线可以看出，递推SOM方法的预测曲线与实际曲线的重合度较高，取得了满意的预测效果。

3 结束语

针对短时交通流预测，本文提出递推SOM方法，包括RecSOM模型和SOMSD模型。该方法不仅考虑当前输入，也能实现对历史事件的记忆最大化。RecSOM模型用带时延的反馈表现递推的概念，SOMSD模型利用获胜神经元的网格坐标表示上下文信息，更适用于结构化数据。上下文信息不仅包含了数据集的拓扑统计特性，还体现了网络自身的变化规律。将递推SOM方法的预测模型应用于两个交通流实例，并在同等情况下与其他预测方法进行对比，结果验证了方法是可行的、有效的。

[1] Li R H,Xu J M,Luo Q,et al.Real-time traffic flow forecasting based on wavelet neural network[J].International Journal of Online Engineering(iJOE),2013,9(3):72-76.

[2] 梁秀霞,胡姗姗,李伟斌.非参数回归算法在短时交通流预测中的应用[J].自动化仪表,2011,33(4):21-23.

[3] 王娇.最小最大概率回归机在短时交通流预测中的应用[J].公路交通科技,2014,31(2):121-127.

[4] Jeong Y S,Byon Y J,Castro-Neto M M,et al.Supervised weighting-online learning algorithm for short-term traffic flow prediction[J].IEEE Transactions on Intelligent Transportation Systems,2013,14(4):1700-1707.

[5] Haykin S S.Neural networks and learning machines[M].New York:Prentice Hall,2009.

[6] Barreto G A.Time series prediction with the self-organizing map:a review[J].Perspectives of Neural-symbolic Integration,Studies in Computational Intelligence,2007,77:135-158.

[7] Hammer B,Micheli A,Sperduti A,et al.A general framework for unsupervised processing of structured data[J].Neuro Computing,2004,57:3-35.

[8] Blohm S.Data mining on sequences with recursive self-organizing maps[D].Bachelor thesis,University of Osnabrück,2003.

[9] Voegtlin T.Recursive self-organizing maps[J].Neural Networks,2002,15(8):979-991.

[10]Hagenbuchner M,Sperduti A,Tsoi A C.A self-organizing map for adaptive processing of structured data[J].IEEE Transactions on Neural Networks,2003,14(3):491-505.

[11]Xie Y,Zhao K,Sun Y,et al.Gaussian processes for short-term traffic volume forecasting[J].Transportation Research Record:Journal of the Transportation Research Board,2010,2165:69-78.

Application of the Recursive SOM Neural Network in Short-term Traffic Flow Prediction

For short-term traffic flow prediction, the method of recursive self-organizing map (SOM) neural network is proposed. On the basis of the associative memory technology of SOM neural network, the ResSOM model considering feedback and the SOMSD model capable using structured information are given respectively. The method of recursive SOM uses full SOM as the replicated neuron, and the combination of historical activities and current information as the input; it learns time series dynamics by training the weight value of neuron and context information. The method of recursive SOM is applied in prediction of measured traffic flow data of an area, and comparison with existing method is conducted, the experimental results show that the method of recursive SOM effectively improves the prediction accuracy; it is superior to other methods under the same circumstances.

Short-term traffic flow Intelligent transportation Self-organizing map Neural network Recursion Prediction

国家自然科学基金资助项目(编号：51467008)；

黄杰(1990-)，女，现为兰州交通大学交通信息工程及控制专业在读硕士研究生；主要从事自组织映射网络在时间序列预测方面的研究。

TP391

A

10.16086/j.cnki.issn1000-0380.201504001

甘肃省高等学校基本科研业务费专项资金项目(编号：620026)。

修改稿收到日期：2014-11-25。