基于主成分的改进马氏距离TOPSIS方法
张 峰,谢振华,程江涛,崔高仑,李 林
(海军航空工程学院青岛校区,山东 青岛 266041)
基于主成分的改进马氏距离TOPSIS方法
张 峰,谢振华,程江涛,崔高仑,李 林
(海军航空工程学院青岛校区,山东 青岛 266041)
针对指标变量线性相关,导致变量协方差矩阵行列式(广义样本方差)为零无法应用马氏距离的情况,采用主成分分析法对指标变量进行线性组合,在不减少信息量的同时,得到少数几个不相关的主成分,由主成分构成的协方差矩阵行列式不再为零。依据降维后的主成分变量,采用基于马氏距离的逼近理想解法对五种预警机探测引导能力进行了排序,经检验其结果与实际情况相符。
逼近理想解法(TOPSIS),主成分,马氏距离,广义样本方差
0 引言
TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)法[1-3]是多属性决策法的一种,它计算简便、评估结果合理、易于被人们理解,因此应用广泛。但TOPSIS法存在不足之处[4]:与理想解欧式距离近的方案可能与负理想解的欧式距离也近,因此,按欧式距离计算方案的相对贴进度并不能反映出方案的优劣性。文献[5]采用基于垂面距离的正交投影法对TOPSIS法进行了改进,消除了上述的不足,但在以理想解点与负理想解点连线为法向量的平面上的方案点与理想解点和负理想解点的欧氏距离都相同,故无法对这些方案点进行排序。此外,由于方案的指标之间难免会有重复的信息,此法无法消除指标间的重复信息,因此,基于垂面距离的正交投影法存在很大缺陷。为了消除以上不足,文献[6]从统计学角度出发,引入基于统计原理的马氏距离来度量方案点之间的距离,且消除了指标间的重复信息,科学、合理地对方案进行了排序。但是,该方法受制于指标变量协方差矩阵为可逆矩阵的限制,如果指标向量组线性相关则无法计算方案点与理想解点的马氏距离。因此,本文应用主成分分析法(principle component analysis,PCA)[7]对指标变量进行信息无损失压缩,即对指标变量进行线性组合,得到少数几个不相关的主成分,因主成分的协方差矩阵为可逆矩阵,从而可以计算方案点与理想解点和负理想解点的马氏距离,依据各方案与理想方案的贴进度对五种预警机的探测引导能力进行了合理排序。
1 TOPSIS的研究现状
1.1 传统TOPSIS法介绍
1.1.1 TOPSIS法概述
TOPSIS法是由Hwang等[8]于1981年首次提出的一种适用于根据多属性指标对多个评价对象进行比较选择的分析方法。它采用加权欧氏距离作为一种测度,来度量各备选方案与理想方案和负理想方案的距离,并依据各备选方案与理想方案的相对贴进度进行排序。
1.1.2 TOPSIS法基本原理
TOPSIS法的应用步骤如下[9]:
Step 1:构建样本数据的评价矩阵

该矩阵中,m表示评价方案的数量,n表示属性指标数量,xij表示第i(i=1,2,…,m)个评价方案的第j(j=1,2,…,n)个属性指标所对应的原始指标值。
Step 2:对矩阵A进行归一化处理,同时消除不同属性指标之间的量纲与数量级影响,从而解决属性指标不可公度问题,即:

其中rij表示第i个评价对象在第j个属性指标下所对应的经过归一化处理后的指标值。
Step 3:将权重矩阵W=(W1,W2,…,Wn)右乘评价矩阵得到价值矩阵:


Step 4:确定理想解S+与负理想解S-,即
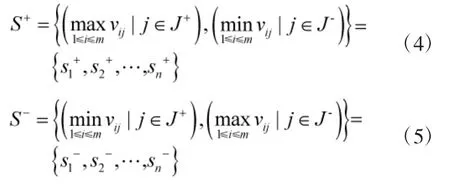
其中,J+为效益型指标,J-为成本型指标。
Step 5:分别计算第i个评价方案到理想解S+的距离以及到负理想解S-的距离Di-,即:

Step 6:计算各评价方案相对贴近度

1.1.3 传统TOPSIS法的缺点分析
传统TOPSIS计算简单,易于理解,但存在许多缺陷:①与理想解欧式距离近的方案可能与负理想解的欧式距离也近,无法对方案进行排序;②变化程度不同的坐标在欧氏距离计算时起着相同的作用,可变性大的指标加权应该小于可变性小的指标;③不同指标向量存在一定程度的相关性,即:Cov(xi,xj)≠0(i≠j),这意味着指标信息重复,因此应用欧氏距离不合理。
1.2 基于正交投影的TOPSIS法的介绍
在对传统TOPSIS法的改进过程中,有许多学者引入基于垂面距离的正交投影法[5],正交投影法是以与理想解的“垂面”距离作为判断方案优劣的标准,它将待评方案点投影到理想解点与负理想解点连线上,与理想解“垂面”距离近且与负理想解的“垂面”距离远,从而克服了上面述及传统TOPSIS法的第1个缺陷,但没有对第2个、第3个缺陷作出改进。
1.3 基于马氏距离的TOPSIS法介绍
1.3.1 马氏距离概述
马氏距离[10]是印度统计学家Mahalanobis于1936年提出的一种统计距离,由于该距离独立于测量尺度,不受坐标之间的量纲影响,采用标准差函数表达式作为指标的权重,使得指标变化值大的内化权重赋值小,克服了在测度距离时各个变化程度不同的指标起相同作用这个缺点,并排除了变量之间不同程度的相关性的干扰。
1.3.2 基于马氏距离的TOPSIS法基本原理[8]
Step 1:构建第i个待评方案、理想解方案和负理想解方案向量

Step 2:第i个待评方案与理想解方案和负理想解方案之间的马氏距离分别为:

其中,C为n个属性变量的协方差矩阵,且为对称矩阵,即
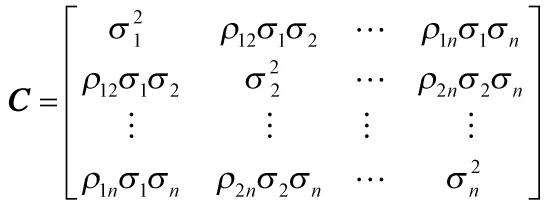
式中C-1为协方差矩阵的逆矩阵,第i个变量与第j个变量之间的相关系数为ρij,σi为第i个变量的标准差。
1.3.3 现有马氏距离TOPSIS法的不足
计算马氏距离时,需要计算C-1,若广义样本方差,意味着构成协方差矩阵的n个列向量线性相关,无法应用马氏距离。
2 基于主成分的马氏距离TOPSIS法的改进
鉴于上面述及的如果指标向量线性相关,无法计算C-1的情况,本文引入主成分分析法对矩阵A进行降维处理,即用少数k个主成分来代替n个属性指标,且k个主成分和n个属性指标所包含的信息相同。具体计算步骤如下:
Step 1[11]:对初始A进行标准化处理

其中,

Step 2:计算标准化数据的相关矩阵

Step 3:求相关矩阵的特征值—特征向量对(λ1,e1),(λ2,e2),…,(λm,em),其中,λ1≥λ2≥…≥λm≥0。则第i个主成分为:
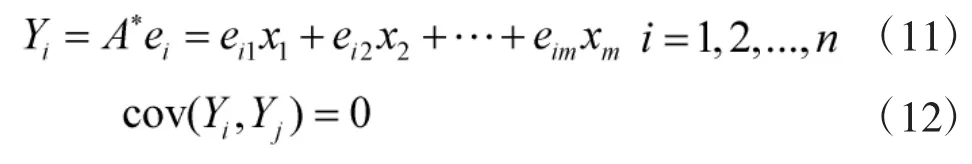
Step 4:利用降维后的主成分指标矩阵,依据基于马氏距离的TOPSIS法进行计算,得出相应的贴进度。
3 算例分析
3.1 改进马氏距离TOPSIS方法计算过程
设五种预警机分别为E-2C、E-3A、A-50、Falcon、E-2T,用V=(v1,v2,v3,v4,v5)表示,其探测引导能力指标有雷达最大探测距离、雷达搜索总方位角、雷达体制、可同时跟踪目标数、可同时引导作战飞机数,用X=(x1,x2,x3,x4,x5)表示。
鉴于预警机保密原因及资料准确程度的问题,算例中的数值为估算值。此外,为了本文计算的需要,特将预警机探测引导能力指标向量组设计为线性相关,其具体数值如表1所示。

表1 预警机探测引导能力评估指标数值
计算初始指标向量的相关矩阵R,其特征值-特征向量对如表2所示。

表2 相关矩阵特征值-特征向量对
利用降维后的主成分指标矩阵,依据基于马氏距离的TOPSIS法进行计算,得出相应的贴进度如表4所示。
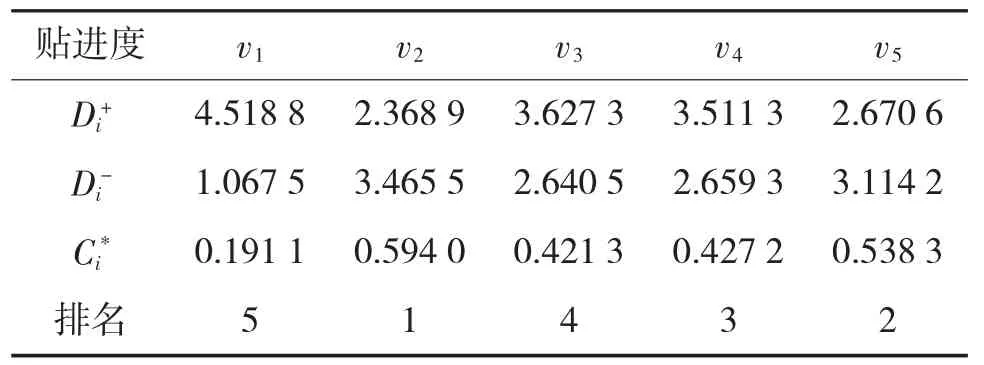
表3 各预警机的相对贴进度及排名
3.2 评价结果分析
采用传统的TOPSIS方法的相应的贴进度及排名如表4所示。

表4 各预警机的相对贴进度及排名
采用正交投影的TOPSIS方法的相应的贴进度及排名如表5所示。
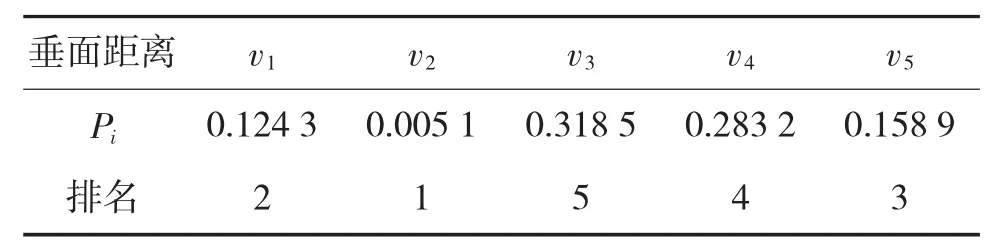
表5 各预警机的相对贴进度及排名
通过对比分析知,采用传统的TOPSIS方法和正交投影的TOPSIS方法的排序结果一致,为v2v1v5v4v3,而采用改进马氏距离的TOPSIS方法结果为v2v5v4v3v1。三种方法均将排在首位,且v5v4v3的排序结果一致,不同的是前两种方法对v5和v1的排序为v1v5,而采用改进马氏距离的TOPSIS方法结果为v5v1,且v3v1,结合实际情况可知,预警机E-2T与E-2C相比在雷达最大探测距离和可同时引导作战飞机数两个指标数值上都具有一定的优势,因此,v5v1更合理。此外,由于五种预警机雷达体制指标数值比较接近,因此,内化于马氏距离之中的权重小,实际预警机雷达体制对其探测引导能力影响很大,所以v3v1相对比较准确。前两种方法与第三种方法计算的排序结果不一致的原因是前两者都存在指标信息重复、且指标相关等问题,后者消除了这两个原因,更科学合理地对预警机的探测引导能力进行了排序。
4 结论
本文针对广义样本方差为零,无法计算变量协方差矩阵逆矩阵的情况,采用主成分分析方法对变量进行降维处理,进而计算出协方差矩阵逆矩阵,应用马氏距离度量了各方案与理想方案的贴进程度,最后对预警机的探测引导能力进行了排序。但是如何在协方差矩阵为非正定矩阵时计算马氏距离的问题没有涉及,应该在这一方面开展相应的研究。
[1]Boran F E,Genc S.A Multi-criteria Intuitionistic Fuzzy Group Decision Making for Supplier Selection with TOPSIS Method[J].Expert Systems with Applications,2009,36(8):11363-11368.
[2] Wu J,Sun J S,Zha Y,et al.Ranking Approach of Cross-efficiency Based on Improved TOPSIS Technique[J].Journal of Systems Engineering and Electronics,2011,22(4):604-608.
[3]Zhou W K,Jiang W C.Two-phase TOPSIS of Uncertain Multi-attribute Group Decision-making[J].Journal of Systems Engineering and Electronics,2010,21(3): 423-430.
[4] Chamodrakas I,LeftheriotisI,Mar-takos D.In-depth Analysis and Simulation Study of an Innovative Fuzzy Approach for Ranking Alternatives in Multiple Attribute Decision Making Problems Based on TOPSIS[J].Applied Soft Comput-ing Journal,2011,11(1):900-907.
[5]华小义,谭景信.基于“垂直”距离的TOPSIS法———正交投影法[J].系统工程理论与实践,2004,52(1): 114-119.
[6]王先甲,汪磊.基于马氏距离的改进型TOPSIS在供应商选择中的应用[J].控制与决策,2012,27(10):1566-1570.
[7]Richard P G,Daniel K,Gregory A.Cherry.Introducing a Unified PCA Algorithm for Model Size Reduction[J].IEEE Transactions on Semiconductor Manufacturing,2010,23(2):201-205.
[8] Hwang C L,Yoon K.Multiple Attribute DecisionMaking: Methods and Applicatios[M].New York:Springer-Verlag,1981.
[9]Vahdani B,Mousavi S M,Tavakkoli-Moghaddam R.Group Decision Malting Based on Novel Fuzzy Modified TOPSIS Method[J].Applied Mathematical Modelling,2011(35):4257-4269.
[10]朱惠倩.聚类分析的一种改进方法[J].湖南文理学院学报:自然科学版,2005,17(3):7-9.
[11]何晓群.多元统计分析[M].北京:中国人民大学出版社,2008.
Method to Improved Mahalanobis Distance of TOPSIS Based on Principal Component
ZHANG Feng,XIE Zhen-hua,CHENG Jiang-tao,CUI Gao-lun,LI Lin
(Qingdao Branch,NAAU,Qingdao 266041,China)
Aim at the thing that indexes are linear correlative,which lead to the emergence of the thing that determinants of covariance matrix of variables(generalized sample-variance)is zero.In this condition,mahalanobis distance calculation can’t go along.Principal component analysis is adopted to combine indexes linearly.At the same time,a few irrelevant principal components are attained,and the indexes information isn’t decreased;accordingly,determinants of covariance matrix of principal components isn’t zero.The method to Mahalanobis distance of TOPSIS based on principal component is adopted to calculate performance guidance of five kinds of early-warning aircraft,and list in order of size. The results are verified by the fact.
TOPSIS,principal component,Mahalanobis distance,generalized sample-variance
TPO159;E92
A
1002-0640(2015)03-0092-04
2014-02-18
2014-03-11
张 峰(1979- ),男,山东淄博人,博士研究生,工程师。研究方向:武器装备综合保障理论与技术,多属性决策评估。

